Оценка надежности

Оценка надежности

СОДЕРЖАНИЕ

    ВВЕДЕНИЕ

    МЕТОДИКА ОЦЕНКИ ВЕРЯТНОСТИ

    ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ РАЗРУШЕНИЯ ПРИ ЗАДАННОМ ЗАПАСЕ ПРОЧНОСТИ.

    СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

ВВЕДЕНИЕ

Совершенство методов и средств диагностики позволяет обнаруживать в элементах конструкций дефекты различного происхождения. В связи с этим возникает задача о допустимости обнаруженных дефектов с точки зрения нормального функционирования и безопасной работы ДЛА. Ситуация, связанная с необходимостью прогнозирования разрушения элементов ДЛА, а также с оценкой риска эксплуатации в условиях неполноты и неопределенности информации о качестве и состоянии ДЛА, является постоянно действующим фактором. Одним из возможных способов реализации прогноза в условиях неопределенности исходной информации является вероятностный подход.

Пусть на некотором участке конструкции имеются дефекты различных типов (объемные и трещиноподобные поверхностные и подповерхностные дефекты, поры, непровары, коррозионные и эрозионные язвы и т.п). Рассмотрим в начале дефекты одного типа. Системой контроля дефект этого типа критического размера l* будет или обнаружен с вероятностью Р>1>(l*), или не обнаружен с вероятностью с вероятностью Н>1>(l*)=1-Р>1>(l*). В первом случае условная вероятность отказа будет равна нулю, т.к обнаруженный дефект критического размера должен быть либо устранен, либо приняты меры для остановки его дальнейшего роста, либо должен быть заменен элемент конструкции с обнаруженным критическим дефектом. Во втором случае условная вероятность отказа равна 1, а безусловная вероятность отказа совпадает с вероятностью Н>1>(l*) необнаружения критического дефекта. При наличии ансамбля дефектов одного типа вероятность отказа определяется вероятностью Н(l) необнаружения хотя бы одного дефекта с критическим размерами.

Таким образом для оценки вероятности отказа конструкции по результатам диагностического контроля нужно уметь вычислять вероятность необнаружения опасных дефектов Н(l).

МЕТОДИКА ОЦЕНКИ ВЕРЯТНОСТИ

Пусть процесс обнаружения дефектов состоит из независимых событий, т.е. обнаружение одного дефекта не влияет на процедуру обнаружения других дефектов. Если это условие выполнено, то множество дефектов образует Пуассоновский поток. Для этого потока вероятность необнаружения к дефектов Q>k>(l) вычисляется по формуле (1):

>> (1)

Здесь v(l)- математическое ожидание числа необнаруженных в результате контроля дефектов размером больше l. Тогда вероятность Н(l) необнаружения хотя бы одного дефекта размером больше l вычисляется как:

>> (2)

Обозначим через (l) математическое ожидание общего числа дефектов определенного типа, размер которых превышает l. Если через P>a>(l) обозначить вероятность обнаружения одного дефекта размером больше l, то (2) будет выглядеть так:

>> (3)

Т.к в результате контроля можно подсчитать только обнаруженные дефекты, то их математическое ожидание очевидно равно:

K(l)=(l)- v(l)= (l)*P>a>(l),

Откуда с учетом [3] следует, что:

>> (4)

В итоге для вероятности Н(l) получим :

>> (5)

В формулы (3) – (5) входит вероятность P>a>(l) обнаружения наугад взятого дефекта размером больше l. Эта вероятность зависит от вероятности P*(l) обнаружения дефекта размером l, локализованного в месте измерения, а также от распределения дефектов по размерам (2):

>> (6)

Здесь F(l)- функция распределения дефектов по размерам,

p(l)=dF(l)/dl- соответствующая плотность вероятности.

Вероятность P*(l) оценивается путем испытаний на эталонных образцах с заданным числом дефектов определенного размера.

Ее статистическая оценка равна отношению числа обнаруженных дефектов заданного размера к их общему числу. Очевидно, что для каждого метода измерений и для каждого типа дефектов имеется свой порог обнаружения l>0>, для которого дефекты размером <l>0> не обнаруживаются с вероятностью близкой к 1. В качестве аппроксимации для функции P*(l) можно взять экспоненциальную зависимость:

>> (7)

с параметром , который оценивается экспериментально. Например, если в результате испытаний получена оценка математического ожидания > > размеров обнаруженных дефектов, то в качестве оценки для параметра  можно взять величину > >. Распределение дефектов по размерам F(l) также аппроксимируется теоретической зависимостью, например распределением Вейбулла (2).

Итак, для дефектов одного типа вероятность отказа при наличии системы контроля за дефектами будет равна:

(8)

Полученные соотношения нетрудно обобщить на случай, когда имеются различные типы дефектов. Пусть число таких типов дефектов равно n, а дефекты каждого типа образуют Пуассоновский ансамбль. Тогда все дефекты также образуют Пуассоновский поток (1) суммарной интенсивностью, равной сумме интенсивностей:

>>>>,

где l>*j >–предельный размер j-го типа дефектов.

С учетом формулы (2) для суммарной вероятности отказов будем иметь: > 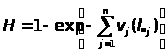>, (9)

где интенсивности потоков пропущенных при контроле дефектов находятся по формуле [4]:

>>>>.

Соответствующие вероятности обнаружения находятся по формуле (6):

>>, в которую входят функция F>j>(l) распределения дефектов j-го типа по размерам и соответствующая плотность вероятности p>j>(l). Условная вероятность обнаружения P>*j>(l) оценивается по формуле (7) с пороговым значением l>0j> и параметром lj для каждого типа дефектов.

Таким образом для оценки вероятности отказов при наличии дефектов различных типов и системе обнаружения дефектов нужно знать следующие вероятностные и числовые характеристики:

    Функции распределения дефектов по размерам;

    Математические ожидания числа обнаруженных дефектов;

    Пороговые значения обнаружения;

    Параметры системы обнаружения дефектов;

    Критические размеры дефектов.

Различные типы предельных состояний характеризуется критическими размерами дефектов, зависящими от свойств материала, от температуры, от условий нагружения и других факторов. Если какие-либо параметры являются случайными, то полученные вероятности имеют смысл условных вероятностей. Основным источником неопределенности является предельное значение размеров дефектов. Этот параметр зависит от ряда случайных факторов. Условные вероятности отказов будут функциями этих параметров. Для вычисления безусловных вероятностей отказов используется формула полной вероятности:

>>.

Здесь p(x>1>,x>2>,…x>m>) – совместная плотность вероятности параметров. Интегрирование проводится по всей области D изменения параметров.

Вероятность отказов H>0> к моменту очередного контроля t=t>0> определяется вероятностью необнаружения дефектов размером l, превышающим критический размер l*. При продолжении эксплуатации дефекты, размеры которых не превышали предельных значений, подрастают и с течением времени могут достичь критических размеров.

Пусть к моменту времени t=t>0> имеется одиночный размером l. Этот дефект системой контроля может быть обнаружен с вероятностью 1-P>a>(l). Рост дефектов будем описывать уравнением (2).

>> (10)

где c и m- эмпирические константы, > >- коэффициент интенсивности напряжений, зависящий от уровня напряжений, от размеров дефекта, от свойств материала и других факторов.

Решение уравнения (10), получаемое, как правило, численно с начальным условием l(t>0>)=l>0>, зависит от ряда случайных факторов. Эта зависимость определяется случайным характером К, неопределенностью свойств материала и т.д. Обозначим вектор случайных параметров через у с компонентами у>1>, у>2>, у>3>…у>р>. Тогда решение уравнения (10) можно представить в виде

l(t)= l(y>1>, y>2>, y>3>…y>p>;t) (11)

К моменту времени t размер дефекта l(t) будет случайным с плотностью вероятности p>l>(l;t), где t играет роль параметра. Для нахождения распределения p>l>(l;t) воспользуемся правилами вычисления распределений для детерминистических функций случайных величин (3). В частности, если имеется детерминистическая функция (11), то функция распределения F>l>(l;t) находится так:

>> (12)

где область интегрирования находится из условия l(t)= l(y>1>, y>2>, y>3>…y>p>;t)< l.

Остаточный ресурс  определяется как продолжительность эксплуатации после очередного контроля, в течение которого размер дефекта подрастает до критического значения l*. Он находится как корень уравнения

l()=l* (13)

Даже при фиксированных значениях l* ресурс будет случайной величиной. Это связано со случайной зависимостью l(t). Дополнительную неопределенность вносит случайный характер критического размера l*, зависящего от случайных факторов. Плотность вероятности находится по тем же правилам, что и распределение (12).

>> (14)

Область интегрирования находится из условия l(t)= l(x>1>, x>2>, x>3>…x>m>;t)< l*. Вероятность отказа по критерию остаточного ресурса находится как вероятность выполнения неравенства l(t)>l*: > >. При известных законах распределения p1(l,t) и pl*(l*), определяемым по формулам (12) и (14), эта вероятность находится как

>> (15)

Формулу (15) можно упростить проинтегрировав по одной из переменных в области D[l,t,l*]:

>> (16)

Другую эквивалентную форму получим, взяв в качестве независимой переменной l*:

>> (17)

Рассмотренная схема оценки вероятности отказов по критерию остаточного ресурса учитывает рост одиночного дефекта. При наличии множества начальных дефектов с различными размерами будем считать, что их рост происходит независимо. Разобьем весь интервал начальных размеров дефектов, как обнаруженных в результате контроля, так и пропущенных, на подинтервалы со средними начальными размерами l>k>. Обозначим через >k> математическое ожидание числа дефектов, попавших в k-ый интервал. Эта величина находится через математическое ожидание k>k> числа обнаруженных в результате контроля дефектов в k-ом интервале и через вероятность их обнаружения Р>а>(l>k>) по формуле: > >.

Суммарная вероятность отказов при наличии множества дефектов находится как:

>> (18)

здесь через H>k>(t) обозначена вероятность отказов, вычисленная по формуле (16) или (17) при начальном размере дефекта l>k>.

Окончательно с учетом вероятности отказов к моменту контроля t>0> для вероятности отказов в момент времени t>t>0> получим:

H(t)=H>0>+H>>(t) (19)

где вероятность H>0 >находится по формуле (8).

По формуле (19) можно оценит увеличение риска с течением времени эксплуатации после очередного контроля. Эта формула позволяет также оценить остаточный ресурс из условия непревышения вероятностью отказов предельного значения H*. Расчетное значение остаточного ресурса * находится как корень уравнения H()=H*.

Учет различных типов дефектов производится по формуле:

>>>> (20)

где вероятности отказов H>j>(t) для каждого типа дефектов находятся согласно (19).

Для численного примера аппроксимируем функцию распределения длин дефектов F(l) и критических дефектов асимптотическими распределениями Вейбулла с параметрами l>0>, l*>0>, l>c>, l*>c>, a, a>1>:

>> (21)

>> (22)

Математическое ожидание числа обнаруженных дефектов аппроксимируем зависимостью с параметрам >1> и l>1>: > >.

Уравнение роста дефектов (10) перепишем в виде:

> > (23)

При =const решение этого уравнения с начальным условием l>k>(t>0>)= l>0k> имеет вид: > > , где m>1>=m/2-1 (24)

Рассматривая параметр напряжения  как случайный с распределением Релея

>> (25)

Найдем распределение длин дефектов F>l>(l>k>;t) по формуле (12), которая примет вид:

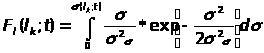>> (26)

где (l>k>;t) – решение уравнения (24) относительно :

>> (27)

После вычисления интеграла (26) получим:

>> (28)

Таким образом, изложенный подход к оценке вероятности отказа элементов конструкций ДЛА по результатам диагностического контроля дефектов позволяет учитывать статистическую информацию о различных типах дефектов, полученную в результате обследования, оценить остаточный ресурс после очередного диагностического обследования.

2. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ РАЗРУШЕНИЯ ПРИ ЗАДАННОМ ЗАПАСЕ ПРОЧНОСТИ.

На основании расчетов в курсе ДиПРД принимаем полученные значения n, k>B1> и t.

n=8000 об/мин, k>B1>=1.8, t=1.800 сек. Принимается, что рассчитываемая деталь работает на режиме нормальной эксплуатации.

Q(t)= *t;

[]=1*10-9 1/ч; (1)

P>разр>(t)=Q(3t>рес>);

Q=q=1*10-9;

Q(3t>рес>)=*3t>рес>=1*10-9*3*0.5=1.5*10-9;

>> ; (2)

>>.

Сравнивая выражение (1) с выражением (2) делаем вывод о том, что рассчитываемая деталь соответствует мировому уровню по обеспечению надежности.

Для повышения уровня безотказности выполняются следующие действия:

определяем коэффициенты вариации предельных свойств конструкции (V>s>) и параметров нагруженности (V>R>).

V>s >выбирается в соответствии с рекомендациями. Принимаем V>s>=0.1.

Коэффициент V>R> получаем расчетным путем:

> >

Далее рассчитываем P>разр>(t) для различных значений коэффициента запаса k>B1 >и коэффициентов вариации (V>s>) и (V>R>) . Для этого расчета используем следующие зависимости:

>>

Таблица 7

V>s>=0.1, V>R> =0.0125

K

Ф()

P>разр>(t)

1

0

0

0.500000

1.2

1.66

0.45150

0.048500

1.4

2.85

0.49780

0.002200

1.6

3.74

0.49990

0.000098

1.8

4.43

0.49999

0.000071

Таблица 7

V>s>=0.12, V>R> =0.015

K

Ф()

P>разр>(t)

1

0

0

0.5000000

1.2

1.38

0.41620

0.0838000

1.4

2.37

0.49110

0.0089000

1.6

3.12

0.49904

0.0009600

1.8

3.69

0.49998

0.0000115

Таблица 7

V>s>=0.08, V>R> =0.01

K

Ф()

P>разр>(t)

1

0

0

0.5000000

1.2

2.07

0.480750

0.0192500

1.4

3.56

0.499805

0.0002000

1.6

4.67

0.499998

0.0000021

1.8

5.54

0.499999

0.0000003

Таблица 7

V>s>=0.12, V>R> =0.0125

K

Ф()

P>разр>(t)

1

0

0

0.5000000

1.2

1.38

0.416200

0.0838000

1.4

2.37

0.491100

0.0089000

1.6

3.12

0.499040

0.0009600

1.8

3.7

0.499988

0.0000115

Таблица 7

V>s>=0.08, V>R> =0.0125

K

Ф()

P>разр>(t)

1

0

0

0.5000000

1.2

2.07

0.4807500

0.0192500

1.4

3.55

0.4997053

0.0002900

1.6

4.67

0.4999979

0.0000021

1.8

5.53

0.4999996

0.0000004

Таблица 7

V>s>=0.1, V>R> =0.015

K

Ф()

P>разр>(t)

1

0

0

0.5000000

1.2

1.65

0.4505000

0.0495000

1.4

2.84

0.4977000

0.0023000

1.6

3.73

0.4997800

0.0002200

1.8

4.43

0.4999929

0.0000021

Таблица 7

V>s>=0.1, V>R> =0.01

K

Ф()

P>разр>(t)

1

0

0

0.5000000

1.2

1.66

0.4515000

0.0485

1.4

2.85

0.4978000

0.0022000

1.6

3.74

0.4999020

0.0000980

1.8

4.44

0.4999929

0.0000021

По полученным значениям P>разр>(t) строится график P>разр>(t)=f(k>B1>)

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

    Болотин В.В. Ресурс машин и конструкций- М.: Машиностроение, 1990.-448с.

    Вентцель Е.С. Теория вероятностей.-М.: Наука, 1969.-576с.

    Гумбель Э. Статистика экстремальных значений.- М.:Мир, 1965.-450с.

    Болотин В.В., Чирков В.П. Асимптотические оценки для вероятности безотказной работы по моделям типа нагрузка-сопротивление// Проблемы машиностроения и надежности машин, 1992,№6 с.3-10