Принятие решений в условиях неопределенности (работа 2)
Принятие решений в условиях неопределенности
Часть I. Принятие решений в условиях неопределенности.
Вариант 15.
( 0 , 1/2 ) ( 6 , 1/4 ) ( 5 , 1/5 ) ( 2 , 1/20 )
( 6 , 1/2 ) ( 2 , 1/4 ) ( 8 , 1/5 ) ( 22 , 1/20 )
( 9 , 1/2 ) ( 4 , 1/4 ) ( 3 , 1/8 ) ( 32 , 1/8 )
( -6 , 1/2 ) ( -4 , 1/4 ) ( -12 , 1/8 ) ( 10 , 1/8 )
В этих строках опускаем дроби:
( 0 6 5 2 )
( 6 2 8 22)
( 9 4 3 32)
( -6 -4 -12 10)
Полученные строки объединяем в матрицу:
0 6 5 2
6 2 8 22
9 4 3 32
-6 -4 -12 10
р>j> = ( 1/2 1/4 1/5 1/20 )
Руководитель, менеджер, обязан разрешать проблемы, встающие перед ним, перед коллективом, которым он руководит. Он обязан принимать решения. В теории принятия решений есть специальный термин: ЛПР — Лицо, Принимающее Решения. Ниже по тексту будем использовать этот термин.
Принять решение — это решить некоторую экстремальную задачу, т.е. найти экстремум некоторой функции, которую называют целевой, при некоторых ограничениях. Например, линейное программирование представляет целый класс таких экстремальных задач. Методы теории вероятностей и математической статистики помогают принимать решения в условиях неопределенности.
Не все случайное можно “измерить” вероятностью. Неопределенность — более широкое понятие. Неопределенность того, какой цифрой вверх ляжет игральный кубик, отличается от неопределенности того, каково будет состояние российской экономики через 15 лет. Кратко говоря, уникальные единичные случайные явления связаны с неопределенностью, массовые случайные явления обязательно допускают некоторые закономерности вероятностного характера.
Предположим, что ЛПР рассматривает несколько возможных решений i = 1,..., m. Ситуация не определена, понятно лишь, что наличествует какой-то из вариантов ј = 1,..., n. Если будет принято i-е решение, а ситуация есть j-я, то фирма, возглавляемая ЛПР, получит доход q>ij>. Матрица Q = (q>ij>) называется матрицей последствий (возможных решений). Какое же решение нужно принять ЛПР? В этой ситуации полной неопределенности могут быть высказаны лишь некоторые рекомендации предварительного характера. Они не обязательно будут приняты ЛПР. Многое будет зависеть от его склонности к риску. Но как оценить риск в данной схеме?
Допустим, мы хотим оценить риск, который несет i-е решение. Нам неизвестна реальная ситуация. Но если бы ее знали, то выбрали бы наилучшее решение, т.е. приносящее наибольший доход. Иначе говоря, если ситуация есть j-я, то было бы принято решение, дающее доход q>j> = max q>ij>. Значит,
i
принимая i-е решение, мы рискуем получить не q>j>, а только q>ij>, значит, принятие i-го решения несет риск недобрать r>ij> = q>j> - q>ij>. Матрица R = (r>ij>) называется матрицей рисков.
Пусть матрица последствий есть Q.
max
0
6 5 2
5
Q = 6 2 8 22 22
9 4 3 32 32
-6 -4 -12 10 10
Составим матрицу рисков R. Имеем q>1> = 5, q>2> = 22, q>3> = 32, q>4> = 10. Следовательно, матрица рисков есть R.
9 0 3 30
R = 3 4 0 10
0 2 5 0
15 10 20 22
Здесь мы впервые встретились с количественной оценкой риска. Несомненно, что риск — одна из важнейших категорий предпринимательской деятельности, неотъемлемая черта этой деятельности. Как известно, предприниматели живут в среднем лучше, чем остальная часть человечества. Это — награда им за риск в один несчастный день оказаться разоренным. Риск — понятие многогранное и мы еще не раз встретимся с ним.
Принятие решений в условиях полной неопределенности.
При принятии решений в условиях полной неопределенности некоторыми ориентирами могут служить следующие правила-рекомендации.
Правило Вальда (правило крайнего пессимизма). Рассматривая i-е решение, будем полагать, что на самом деле ситуация складывается самая плохая, т.е. приносящая самый малый доход a>i >= min q>ij>. Но теперь уже выберем решение с наибольшим a>i0>. Итак, правило Вальда рекомендует принять решение i>0> такое, что a>i0> = max = max (min q>ij>).
min
0 6 5 2 0
Q = 6 2 8 22 2
9 4 3 32 3
-6 -4 -12 10 -12
Так, в вышеуказанном примере имеем a>1> = 0, a>2> =2, a>3> = 3, a>4> = -12. Теперь из чисел 0, 2, 3, -12 находим максимальное. Это — 3. Значит, правила Вальда рекомендует принять 3-е решение. Данному правилу следует человек, боящийся риска.
Правило Сэвиджа (правило минимального риска). Данному правилу следует человек, боящийся риска. При применении этого правила анализируется матрица рисков R = (r>ij>). Рассматривая i-е решение, будем полагать, что на самом деле складывается ситуация максимального риска b>i> = max r>ij>. Но
j
теперь уже выберем решение i>0> с наименьшим b>i0>. Итак, правило Сэвиджа рекомендует принять решение i>0> такое, что b>i0> = min b>i> = min (max r>ij>).
i j
max
9 0 3 30 30
R = 3 4 0 10 10
0 2 5 0 5
15 10 20 22 22
Так, в вышеуказанном примере имеем b>1> = 30, b>2> =10, b>3> = 5, b>4> = 22. Теперь из чисел 30, 10, 5, 22 находим минимальное. Это — 5. Значит, правило Сэвиджа рекомендует принять 3-е решение.
Правило “розового оптимизма”. ЛПР считает, что для него сложится самая благоприятная ситуация, т.е. он получит самый большой доход в результате своей деятельности
c>i> = max q>ij>. Теперь выберем решение i>0> с наибольшим c>i0>. Итак,
j
правило “розового оптимизма рекомендует принять решение i>0> такое, что c>i0> = max (max q>ij>).
max
0
6 5 2
6
Q = 6 2 8 22 22
9 4 3 32 32
-6 -4 -12 10 10
Так, в вышеуказанном примере имеем с>1> = 6, с>2> = 22, с>3> = 32, с>4> = 10. Теперь из чисел 6, 22, 32, 10 берем максимальное. Это — 32. Значит, правило “розового оптимизма” рекомендует 3-е решение.
Правило Гурвица (взвешивающее пессимистический и оптимистический подходы к ситуации). Принимается решение i, на котором достигается максимум min q>ij> + (1 - max q>ij>где 0 Значение выбирается из субъективных соображений. Если приближается к единице, то правило Гурвица приближается к правилу Вальда, при приближениик нулю правило Гурвица приближается к правилу “розового оптимизма”.
Возьмем = 1/2.
max min
0 6 5 2 6 0
Q = 6 2 8 22 22 2
9 4 3 32 32 3
-6 -4 -12 10 10 -12
i>1> = ½ * 6 + ( 1- ½ ) * 0 = 3
i>2> = ½ * 22 + ( 1 - ½ ) * 2 = 12
i>3> = ½ * 32 + ( 1 - ½ ) * 3 = 17.5
i>4> = ½ * 10 + ( 1 - ½ ) * ( -12 ) = -1
Итак, мы имеем i>1> = 3, i>2> = 12, i>3> = 17.5, i>4> = -1. Теперь из чисел 3, 12, 17.5, -1 берем максимальное. Это — 17.5. Значит, правило Гурвица рекомендует 3-е решение.
Принятие решений в условиях частичной неопределенности.
Предположим, что в рассматриваемой схеме известны вероятности p>j> того, что реальная ситуация развивается по варианту j. Именно такое положение называется частичной неопределенностью. Как здесь принимать решение? Можно выбрать одно из следующих правил.
Правило максимизации среднего ожидаемого дохода. Доход, получаемый фирмой при реализации i-го решения,
является случайной величиной Q>i> с рядом распределения
-
q>i1>
. . .
q>in>
p>1>
p>n>
Математическое
ожидание MQ>i>и
есть средний ожидаемый доход, обозначаемый
также Q>i>.
Итак, правило рекомендует принять
решение, приносящее максимальный средний
ожидаемый доход.
В
приведенном примере вероятности такие
(1/2, 1/4, 1/5,
1/20).
0 6 5 2
Q = 6 2 8 22
9 4 3 32
-6 -4 -12 10
р>j> = ( 1/2 1/4 1/5 1/20 )
0
6 5
2
Q>1>
:
1/2 1/4 1/5 1/20
6
2 8 22
Q>2>
:
1/2 1/4 1/5 1/20
9
4 3 32
Q>3>
:
1/2 1/4 1/5 1/20
-6
-4 -12 10
Q>4>
:
1/2 1/4 1/5 1/20
Q>1> = 6/4 + 5/5 + 2/20 = 1,5 + 1 +0,1 = 2,6
Q>2> = 6/2 + 2/4 + 8/5 + 22/20 = (30+5+16+11)/10 = 62/10 = 6,2
Q>3> = 9/2 + 4/4 + 3/5 + 32/20 = (45+10+6+16)/10 = 77/10 = 7,7
Q>4> = - 6/2 - 4/4 - 12/5 + 10/20 = (-30-10-24+5)/10 = - 59/10 = -5,9
Максимальный средний ожидаемый доход равен 7.7, что соответствует 3-му решению.
Правило минимизации среднего ожидаемого риска. Риск фирмы при реализации i-го решения является случайной величиной R>i> с рядом распределения
|
r>i1> |
. . . |
r>in> |
|
p>1 > |
p>n> |
Математическое
ожидание M[R>i>]
и
есть средний ожидаемый риск, обозначаемый
также R>i>.
Правило рекомендует принять решение,
влекущее минимальный средний ожидаемый
риск.
Вычислим
средние ожидаемые риски.
9
0 3 30
R = 3 4 0 10
0 2 5 0
15 10 20 22
р>j> = ( 1/2 1/4 1/5 1/20 )
9
0 3 30
R>1>
:
1/2 1/4 1/5 1/20
3
4 0 10
R>2>
:
1/2 1/4 1/5 1/20
0
2 5 0
R>3>
:
1/2 1/4 1/5 1/20
15
10 20 22
R>4>
:
1/2 1/4 1/5 1/20
R>1> = 9/2 + 3/5 + 30/20 = (45+6+15)/10 = 66/10 = 6.6
R>2 >= 3/2 + 4/4 +10/20 = 1.5 + 1 +0.5 = 3
R>3> = 2/4 + 5/5 = 15/10 = 1.5
R>4> = 15/2 + 10/4 + 20/5 + 22/20 = (150+50+80+22)/20 = 302/20 = 15.1
Минимальный средний ожидаемый риск равен 1.5, что соответствует 3-му решению.
Иногда в условиях полной неопределенности применяется следующее правило.
Правило Лапласа равновозможности, когда все вероятности p считаются равными. После этого можно выбрать какое-нибудь из двух приведенных выше правил-рекомендаций принятия решений.
Правило максимизации среднего ожидаемого дохода.
|
Q = |
0 6 5 2 6 2 8 22 9 4 3 32 6 -4 -12 10 |
р>j> = ( 1/4 1/4 1/4 1/4 )
0
6 5
2
Q>1>
:
1/4 1/4 1/4 1/4
6
2 8 22
Q>2>
:
1/4 1/4 1/4 1/4
9
4 3 32
Q>3>
:
1/4 1/4 1/4 1/4
-6
-4 -12 10
Q>4>
:
1/4 1/4 1/4 1/4
Q>1>
= (6+5+2)/4 = 13/4 = 3,25
Q>2> = (6+2+8+22)/4 = 38/4 = 9,5
Q>3> = (9+4+3+32)/4 = 48/4 =12
Q>4> = (-6-4-12+10)/4 = -12/4 = -3
Максимальный средний ожидаемый доход равен 12, что соответствует 3-му решению.
Правило минимизации среднего ожидаемого риска.
9
0 3 30
R = 3 4 0 10
0 2 5 0
15 10 20 22
р>j> = ( 1/2 1/4 1/5 1/20 )
9
0 3 30
R>1>
:
1/4 1/4 1/4 1/4
3
4 0 10
R>2>
:
1/4 1/4 1/4 1/4
0
2 5 0
R>3>
:
1/4 1/4 1/4 1/4
15
10 20 22
R>4>
:
1/4 1/4 1/4 1/4
R>1> = (9+3+30)/4 = 42/4 = 10,5
R>2 >= (3+4+10)/4 = 17/4 = 4,25
R>3> = (2+5)/4 = 7/4 = 1,75
R>4> = (15+10+20+22)/4 = 67/4 = 16,75
Минимальный средний ожидаемый риск равен 1.75, что соответствует 3-му решению.
При данных вероятностях состояний теперь требуется проанализировать семейство из 4-х операций: каждая операция имеет две характеристики — средний ожидаемый доход и средний ожидаемый риск. Точка (q’, r’) доминирует точку (q, r), если q’q и r’r. Точка, не доминируемая никакой другой, называется оптимальной по Парето.
Нанесем для каждой операции эти характеристики на плоскую систему координат для выявления операции, оптимальной по Парето, доход по вертикали и риск по горизонтали.
q
2.6 6.2 7.7 -5.9
r 6.6 3 1.5 15.1
Получим четыре точки. Чем выше точка (q, r), тем доходнее операция, чем правее точка, тем более она рисковая. Значит, нужно выбирать выше и левее. Это точка Q>3> (7.7, 1.5). Она является оптимальной по Парето, т.к. доминирует остальные точки.
Затем найдем выпуклую оболочку множества полученных точек и дадим интерпретацию точек полученной выпуклой оболочки.
Точка Q>5> находится на равных расстояниях от точек Q>1> и Q>4>, и соответственно имеет координаты (10.9, -1.7). Аналогично, точка Q>6>> > расположена между точками Q>1>> >и Q>2> и имеет координаты (4.8, 4.4).
Байесовский подход к принятию решений.
Предположим, предприниматель раздумывает над выбросом на рынок нового перспективного товара. Но он не знает, “пойдет” ли товар. Для уточнения ситуации он производит пробную партию и смотрит, как он раскупается. После этого ситуация становится более определенной, более прогнозируемой. Для уточнения этой ситуации можно выпустить еще одну пробную партию и проанализировать какие-нибудь другие моменты.
В
общем, байесовский подход выглядит
следующим образом. Предположим, мы имеем
вероятностный прогноз ситуации S:
P(S=H>i>)=p>i>.
Имея такой прогноз, можно найти средний
ожидаемый доход >
>
или средний
ожидаемый риск>
>.
Рассмотрим возможность проведения
пробной операции, которая уточнит {p>i>}.
Новое распределение вероятностей есть
{p>i>’}.
Новому распределению вероятностей
соответствуют новые характеристики:
средний ожидаемый доход>
>,
средний ожидаемый риск>
>.
Если ЛПР решит, что при уточнении пробная
операция оправдывается (например, если
увеличение среднего ожидаемого дохода
превышает затраты на проведение пробной
операции), то он ее проводит.
0
6 5 2
Q = 6 2 8 22
9 4 3 32
-6 -4 -12 10
р>j>’ = ( 1/6 1/6 1/3 1/3 )
0
6 5
2
Q>1>’
:
1/6 1/6 1/3 1/3
6
2 8 22
Q>2>’
:
1/6 1/6 1/3 1/3
9
4 3 32
Q>3>’
:
1/6 1/6 1/3 1/3
-6
-4 -12 10
Q>4>’
:
1/6 1/6 1/3 1/3
Q>1>‘=
6/6 + 5/3 + 2/3
= 20/6
Q>2>‘ = 6/6 + 2/6 + 8/3+ 22/3 = 68/6
Q>3>‘ = 9/6 + 4/6 + 3/3 + 32/3 = 83/6
Q>4>‘ = - 6/2 - 4/4 - 12/5 + 10/20 = -14/6
Наибольший доход при пробной операции будет получен при 3-ем решении. Теперь выясним, стоит ли производить пробную операцию, т.е. найдем разность между средним ожидаемым доходом от основной операции (см. Правило максимизации среднего ожидаемого дохода) и полученными в результате пробной операции данными, (83/6 - 7,7 = 184/30 = 92/15 6,13). В итоге можно сказать, что стоимость пробной операции в данном примере не должна превышать 6,13.
Для нахождения лучших операций иногда применяют подходящую взвешивающую формулу, которая для пар (Q, r) дает одна число, по которому и определяют лучшую операцию.
Для анализа ситуаций можно применить взвешивающую формулу E(Q, r) = 4Q - r. Данная формула говорит, что доход ценится в четыре раза больше, чем риск, т.е. увеличение риска на 4 компенсируется увеличением дохода на единицу.
E>1> = 4*2.6 - 6.6 = 3.8
E>2> = 4*6.2 - 3 = 21.8
E>3> = 4*7.7 - 1.5 = 29.3
E>4> = 4*(-5.9) - 25.1 = -48.7
Согласно этой формуле лучшей операцией считается операция № 3, а худшей — операция № 4.
Часть I I. Анализ доходности и рискованности финансовых операций.
( 10, 1/4 ) ( 8, 1/4 ) ( 2, 1/3 ) ( 4, 1/6 )
( -6, 1/4 ) ( -2, 1/4 ) ( 10, 1/3 ) ( -6, 1/6 )
( 10, 1/3 ) ( 2, 1/3 ) ( 4, 1/6 ) ( 16, 1/6 )
( -6, 1/3 ) ( 15, 1/3) ( -4, 1/6 ) ( 3, 1/6 )
Составим матрицу Q.
10
8
2
4
Q = -6 -2 10 -6
10 2 4 16
-6 15 -4 3
p>j >= ( 1/4 1/4 1/3 1/6 )
Риск как среднее квадратическое отклонение.
Риск
как среднее квадратическое отклонение
— еще одно понимание риска. Рассмотрим
какую-нибудь операцию, доход которой
есть случайная величина Q.
Как уже указывалось, средний ожидаемый
доход — это математическое ожидание
случайно величины Q.
А вот среднее квадратическое отклонение
>Q>=
>
>
—
это мера разбросанности возможных
значений дохода вокруг среднего
ожидаемого дохода. Напомним, что D[Q]
= M[(Q - m>Q>)2].
Найдем риски в их новом определении r>i> доходов Q>i>.
10 8 2 4
Q = -6 -2 10 -6
10 2 4 16
-6 15 -4 3
p>j >= ( 1/4 1/4 1/3 1/6 )
10
8
2
4
Q>1>
:
1/4 1/4 1/3 1/6
-6
-2 10 -6
Q>2>
:
1/4 1/4 1/3 1/6
10
2 4 16
Q>3>
:
1/4 1/4 1/3 1/6
-6
15 -4 3
Q>4>
:
1/4 1/4 1/3 1/6
>
>
=
10/4+8/4+2/3+4/6
= 70/12 5.83
>
>
=
-6/6-2/4+10/3-6/6 = 4/12 0.33
>
>
=
10/4+2/4+4/3+16/6 = 84/12 = 7
>
>
=
-6/6+15/4-4/3+3/6 = 17/12
1.42
D>1 >= 2384/144 16.56 r>1 >4.07
D>2> = 443/9 49.22 r>2 >7.02
D>3> = 25 r>3> = 5
D>4> = 10091/144 70.08 r>4 >8.37
Нанесем
средние ожидаемые доходы и риски на
плоскость — доход >
>
откладываем по вертикали, а риски — по
горизонтали.
Получили четыре точки. Чем выше точка (q, r), тем более доходная операция, чем точка правее — тем более она рисковая. Значит, нужно выбирать точку левее и выше. Точка (q’, r’) доминирует точку (q, r), если q’q и r’r. В данном примере точка Q>3> доминирует точки Q>2> и Q>4>, точка Q>1> доминирует точки Q>2> и Q>4>. Точки Q>1> и Q>3> несравнимы — доходность 3-ей больше, но и риск ее тоже больше. Точка, не доминируемая никакой другой, называется оптимальной по Парето, а множество всех таких точек называется множеством оптимальности по Парето. Легко видеть, что если из рассмотренных операций надо выбрать лучшую, то ее обязательно надо выбирать из операций, оптимальный по Парето.
Предположим, что все операции независимы друг от друга, тогда можно выяснить, нет операции, являющейся линейной комбинацией основных операций, более хорошей, чем имеющиеся.
>
>
>
>
>
>
>
>
Теперь
найдем >
>,
при которой риск будет минимальным.
Т.к. >
>стремится
к минимуму, то >
>
также стремиться к минимуму.
>
>
>
>
График
данной функции представляет собой
параболу, ветви направлены вверх, значит,
минимальное значение данной функции
будет в точке перегиба — операция,
являющаяся линейной комбинацией основных
операций, будет иметь минимальный риск
при >
>.
Этот риск будет равен 3.38, а доход
соответственно 6,08.
Полученная
точка Q’(6.08,
3.38) доминирует точку Q>1>(5.83,4.07).
Для нахождения лучших операций иногда применяют подходящую взвешивающую формулу, которая для пар (q, r) дает одно число, по которому и определяют лучшую операцию.
Для анализа ситуаций применим взвешивающую формулу E(Q, r) = 4Q - r. Данная формула говорит, что доход ценится в четыре раза больше, чем риск, т.е. увеличение риска на 4 компенсируется увеличением дохода на единицу.
Тогда для 1-ой операции Е = 19.25, для 3-ей операции Е = 23. При сравнении результатов анализа видно, что при данном отношении к рискованности операций лучшей является 3-я операция.
Часть III. Анализ денежных потоков.
Анализ одномерных денежных потоков.
Исходные данные: ежедневные суммарные зачисления по счетам юридических лиц за апрель месяц.
|
число месяца |
день недели |
сумма (тыс. руб) |
|
1 |
ср |
47 |
|
2 |
чт |
44 |
|
3 |
пт |
31 |
|
4 |
сб |
28 |
|
5 |
вс |
|
|
6 |
пн |
42 |
|
7 |
вт |
48 |
|
8 |
ср |
39 |
|
9 |
чт |
40 |
|
10 |
пт |
38 |
|
11 |
сб |
15 |
|
12 |
вс |
|
|
13 |
пн |
45 |
|
14 |
вт |
53 |
|
15 |
ср |
41 |
|
16 |
чт |
27 |
|
17 |
пт |
56 |
|
18 |
сб |
25 |
|
19 |
вс |
|
|
20 |
пн |
51 |
|
21 |
вт |
32 |
|
22 |
ср |
49 |
|
23 |
чт |
21 |
|
24 |
пт |
35 |
|
25 |
сб |
13 |
|
26 |
вс |
|
|
27 |
пн |
58 |
|
28 |
вт |
59 |
|
29 |
ср |
29 |
|
30 |
чт |
30 |
|
числовой ряд (х>i>) |
частота (m>i>) |
частость (> |
выборочная
функция распределения> |
|
13 |
1 |
0,04 |
0,04 |
|
15 |
1 |
0,04 |
0,08 |
|
21 |
1 |
0,04 |
0,12 |
|
25 |
1 |
0,04 |
0,15 |
|
27 |
1 |
0,04 |
0,19 |
|
28 |
1 |
0,04 |
0,23 |
|
29 |
1 |
0,04 |
0,27 |
|
30 |
1 |
0,04 |
0,31 |
|
31 |
1 |
0,04 |
0,35 |
|
32 |
1 |
0,04 |
0,38 |
|
35 |
1 |
0,04 |
0,42 |
|
38 |
1 |
0,04 |
0,46 |
|
39 |
1 |
0,04 |
0,50 |
|
40 |
1 |
0,04 |
0,54 |
|
41 |
1 |
0,04 |
0,58 |
|
42 |
1 |
0,04 |
0,62 |
|
44 |
1 |
0,04 |
0,65 |
|
45 |
1 |
0,04 |
0,69 |
|
47 |
1 |
0,04 |
0,73 |
|
48 |
1 |
0,04 |
0,77 |
|
49 |
1 |
0,04 |
0,81 |
|
51 |
1 |
0,04 |
0,85 |
|
53 |
1 |
0,04 |
0,88 |
|
56 |
1 |
0,04 |
0,92 |
|
58 |
1 |
0,04 |
0,96 |
|
59 |
1 |
0,04 |
1,00 |
>=m>i>/n)
>
График
выборочной функции распределения >
>.
Теперь
построим интервальный вариационный
ряд. Рассчитаем длину интервала по
формуле >
>,
где а
— верхняя граница и b
— нижняя
граница для интервалов, v
— количество
интервалов. Для данного примера а
= 59,
b = 13,
v
=
6, а h
= 9.
|
интер-валы [a>i>-a>i+1>) |
сере- дина интер-вала (y>i>) |
частота (m>i>) |
частость (> |
выборочная функция распределе-ния > |
выборочная плотность (> |
|
9-18 |
13,5 |
2 |
0,08 |
0,08 |
0,22 |
|
18-27 |
22,5 |
2 |
0,08 |
0,16 |
0,22 |
|
27-36 |
31,5 |
7 |
0,27 |
0,43 |
0,78 |
|
36-45 |
40,5 |
6 |
0,23 |
0,66 |
0,67 |
|
45-54 |
49,5 |
5 |
0,19 |
0,85 |
0,56 |
|
54-63 |
58,5 |
4 |
0,15 |
1 |
0,44 |
>)
>)
График
функции распределения >
>
выглядит следующим образом.
Многоугольник интервальных частостей дает более наглядное представление о закономерности изменения ежедневных денежных потоков, т.к. суммы зачислений в разные дни различны и их можно анализировать только по их вхождению в какой-либо интервал.
Выборочное среднее считается следующим способом:
непосредственно по исходным данным >
>,
>
>.по дискретному вариационному ряду
>
>,
где v
— число
вариантов выборки, но в данном примере
v
=
n.
>
>.
по интервальному вариационному ряду
>
>,
таким образом можно найти лишь приближенное
значение выборочной средней. >
>.
Аналогом дисперсии является выборочная дисперсия:
непосредственно по исходным данным >
>,
>
>.по дискретному вариационному ряду >
>,>
>.по интервальному вариационному ряду приблизительное значение >
>,
>
>.
Среднее квадратическое отклонение рассчитывается как квадратный корень из дисперсии.
>
>>
>>
>
Исследуемая нами большая совокупность называется генеральной совокупностью. Теоретически может быть бесконечной В данном примере выборка состоит из 26 элементов. Понятия генеральной совокупности и случайной величины взаимозаменяемы.
Любая функция от выборки называется статистикой.
Пусть
—
некоторый параметр с.в. Х. Мы хотим
определить хотя бы приближенно, значение
этого параметра. С этой целью подбираем
статистику >
>,
которая должна оценивать, может быть
приближенно, параметр .
Заметим,
что любая статистика есть с.в., поскольку
она определена на выборках. Статистику
>
>,
определенную на выборках объемом n,
будем обозначать>
>.
Статистика должна удовлетворять следующим требованиям:
состоятельность. Статистика-оценка должна сходиться к оцениваемому параметру при >
>.несмещенность. >
>
для всех достаточно больших n.
Генеральная
средняя удовлетворяет обоим условиям,
поэтому составляет >
>,
но генеральная дисперсия удовлетворяет
лишь первому условия, поэтому ее
“подправляют”, умножая на >
>.
В результате, >
>.
Это и является несмещенной оценкой
генеральной дисперсии.
Для
построения графика выборочной функции
плотности рассчитывается выборочная
плотность >
>
(см. выше).
Теперь
отметим на графике >
>
и интервалы >
>и
>
>,
если >
>.
Площадь
многоугольника, опирающегося на интервал
>
>,
примерно равна 3/4, а площадь многоугольника,
опирающегося на интервал>>,
равна единице.
Предположим,
что размер ежедневного суммарного
зачисления по счетам юридических лиц,
обозначим его через случайную величину
Х,
имеет нормальный закон распределения
>
>,
тогда плотность распределения вероятностей
равна >
>,
а функция распределения >
>.
>
>
Отметим полученные точки на графике
Положение
о нормальном законе распределения не
противоречит исходным данным.
>
>
Вероятность
попадания ежедневного суммарного
зачисления по счетам юридических лиц
в интервал >
>
равна 0.364,
в интервал >
>
— 0,996.
Теперь рассчитаем, за сколько дней надо иметь информацию, чтобы с вероятностью не менее 0.9 можно было ожидать, что вычисленное по этой информации среднее зачисление отличается от генерального среднего зачисления по абсолютной величине не более, чем на 10% величины среднего зачисления.
Используя неравенство Чебышева.
>
>
Используя центральную предельную теорему.
>
>
Исходные данные — ежедневные суммарные списания со счетов юридических лиц за апрель месяц.
|
число месяца |
день недели |
сумма (тыс. руб) |
|
1 |
ср |
46 |
|
2 |
чт |
54 |
|
3 |
пт |
42 |
|
4 |
сб |
28 |
|
5 |
вс |
|
|
6 |
пн |
57 |
|
7 |
вт |
26 |
|
8 |
ср |
48 |
|
9 |
чт |
45 |
|
10 |
пт |
32 |
|
11 |
сб |
29 |
|
12 |
вс |
|
|
13 |
пн |
52 |
|
14 |
вт |
33 |
|
15 |
ср |
50 |
|
16 |
чт |
22 |
|
17 |
пт |
36 |
|
18 |
сб |
14 |
|
19 |
вс |
|
|
20 |
пн |
59 |
|
21 |
вт |
49 |
|
22 |
ср |
30 |
|
23 |
чт |
31 |
|
24 |
пт |
43 |
|
25 |
сб |
16 |
|
26 |
вс |
|
|
27 |
пн |
40 |
|
28 |
вт |
41 |
|
29 |
ср |
39 |
|
30 |
чт |
62 |
Построим интервальный вариационный ряд и график выборочной функции плотности.
|
интер-валы [a>i>-a>i+1>) |
сере- дина интер-вала (y>i>) |
частота (m>i>) |
частость (> |
выборочная функция распределе-ния > |
выборочная плотность (> |
|
8-16 |
12 |
1 |
0,04 |
0,04 |
0,005 |
|
16-24 |
20 |
2 |
0,08 |
0,12 |
0,010 |
|
24-32 |
28 |
5 |
0,19 |
0,31 |
0,024 |
|
32-40 |
36 |
4 |
0,15 |
0,46 |
0,019 |
|
40-48 |
44 |
6 |
0,23 |
0,69 |
0,029 |
|
48-56 |
52 |
5 |
0,19 |
0,88 |
0,024 |
|
56-64 |
60 |
3 |
0,12 |
1,00 |
0,014 |
Выборочная функция плотности.
Найдем несмещенные выборочные оценки
генеральной средней >
>дисперсии >
>,
>
>.
Предположим,
что размер ежедневных суммарных списаний
со счетов юридических лиц — нормально
распределенная случайная величина,
тогда функция плотности >
>.
>
>
>
>
Нанесем точки на график
Предположение о нормальном законе распределении не противоречит исходным данным.
Анализ двумерных денежных потоков.
Исходные данные: ежедневные суммарные зачисления и списания со счетов юридических лиц за апрель месяц.
|
число месяца |
день недели |
сумма зачислений (тыс. руб) |
сумма списаний (тыс. руб) |
|
1 |
ср |
47 |
46 |
|
2 |
чт |
44 |
54 |
|
3 |
пт |
31 |
42 |
|
4 |
сб |
28 |
28 |
|
5 |
вс |
||
|
6 |
пн |
42 |
57 |
|
7 |
вт |
48 |
26 |
|
8 |
ср |
39 |
48 |
|
9 |
чт |
40 |
45 |
|
10 |
пт |
38 |
32 |
|
11 |
сб |
15 |
29 |
|
12 |
вс |
||
|
13 |
пн |
45 |
52 |
|
14 |
вт |
53 |
33 |
|
15 |
ср |
41 |
50 |
|
16 |
чт |
27 |
22 |
|
17 |
пт |
56 |
36 |
|
18 |
сб |
25 |
14 |
|
19 |
вс |
||
|
20 |
пн |
51 |
59 |
|
21 |
вт |
32 |
49 |
|
22 |
ср |
49 |
30 |
|
23 |
чт |
21 |
31 |
|
24 |
пт |
35 |
43 |
|
25 |
сб |
13 |
16 |
|
26 |
вс |
||
|
27 |
пн |
58 |
40 |
|
28 |
вт |
59 |
41 |
|
29 |
ср |
29 |
39 |
|
30 |
чт |
30 |
61 |
Построим двумерную корреляционную таблицу:
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
||
|
j |
Y \ X |
13,5 |
22,5 |
31,5 |
40,5 |
49,5 |
58,5 |
> |
|
1 |
12 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
2 |
20 |
1 |
0 |
1 |
0 |
0 |
0 |
2 |
|
3 |
28 |
1 |
1 |
1 |
0 |
2 |
0 |
5 |
|
4 |
36 |
0 |
0 |
1 |
1 |
1 |
1 |
4 |
|
5 |
44 |
0 |
0 |
2 |
1 |
1 |
2 |
6 |
|
6 |
52 |
0 |
0 |
1 |
3 |
1 |
0 |
5 |
|
7 |
60 |
0 |
0 |
1 |
1 |
1 |
0 |
3 |
|
n>i> |
2 |
2 |
7 |
6 |
6 |
3 |
26 |
|
|
> |
24 |
20 |
40 |
49 |
41 |
41 |
||
|
> |
0 |
0 |
0,57 |
0,33 |
0,33 |
0,33 |
>
>
>
Общая
средняя >
>,
>
>.
Общая
дисперсия >
>
, >
>
Средняя
из групповых дисперсий >
>,
>
>.
Дисперсия
групповых средних >
>,
>
>
Выборочная
средняя и дисперсия компоненты Х : >
>
и >
>
(расчеты см. выше).
График поля корреляции и линия групповых средних компоненты Y.
|
Y\X=12 |
13,5 |
22,5 |
31,5 |
40,5 |
49,5 |
58,5 |
|
0 |
1 |
0 |
0 |
0 |
0 |
M[Y/X=12] = 22,5
D[Y/X=12] = 0
|
Y\X=20 |
13,5 |
22,5 |
31,5 |
40,5 |
49,5 |
58,5 |
|
1/2 |
0 |
1/2 |
0 |
0 |
0 |
M[Y/X=20] = 22,5
D[Y/X=20] = 81
|
Y\X=28 |
13,5 |
22,5 |
31,5 |
40,5 |
49,5 |
58,5 |
|
1/5 |
1/5 |
1/5 |
0 |
2/5 |
0 |
M[Y/X=28] = 33,3
D[Y/X=28] = 207,36
|
Y\X=36 |
13,5 |
22,5 |
31,5 |
40,5 |
49,5 |
58,5 |
|
0 |
0 |
1/4 |
1/4 |
1/4 |
1/4 |
M[Y/X=36] = 45
D[Y/X=36] = 101,25
|
Y\X=44 |
13,5 |
22,5 |
31,5 |
40,5 |
49,5 |
58,5 |
|
0 |
0 |
2/6 |
1/6 |
1/6 |
2/6 |
M[Y/X=44] = 45
D[Y/X=44] = 128,25
|
Y\X=52 |
13,5 |
22,5 |
31,5 |
40,5 |
49,5 |
58,5 |
|
0 |
0 |
1/5 |
3/5 |
1/5 |
0 |
M[Y/X=52] = 40,5
D[Y/X=52] =32,4
|
Y\X=60 |
13,5 |
22,5 |
31,5 |
40,5 |
49,5 |
58,5 |
|
0 |
0 |
1/3 |
1/3 |
1/3 |
0 |
M[Y/X=60] = 40,5
D[Y/X=60] = 54
D[Y, ост] = 121,25
Коэффициент детерминации К = 1 - 121,25/169 = 0,28
Корреляционное
отношение >
>
(близость корреляционного отношения к
единице указывает на то, что зависимость
Y
от Х близка к функциональной).
Корреляционный момент
>
>,
>
>
Коэффициент
корреляции >
>,
>
>.
Показывает степень линейной зависимости
между случайными величинами.
Выборочный
коэффициент детерминации >
>,
равен 1,008.
Выборочное
корреляционное отношение >
>,
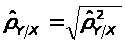равен 1,004.
Отношение коэффициента детерминации и коэффициента корреляции равно 0,76.
Уравнение
регрессии y=0.37x+25.57.
Прямая регрессии обязательно проходит
через точку >
>.
>
>
Теперь оценим, на сколько процентов (по отношению к размеру среднего ежедневного зачисления) изменится ожидаемое значение ежедневного списания при увеличении на 1% (по отношению к размеру ежедневного списания) ежедневного зачисления.
y=0.37x+25.57
(0,37*40,4+25,57)/(0,37*40+25,57)=1,004
Значит, при увеличении ежедневного зачисления на 1% ожидаемое значение ежедневного списания увеличится на 0,4%.