Теорема Штольца (работа 2)

Теорема Штольца

Содержание работы:

Формулировка и доказательство теоремы Штольца.

Применение теоремы Штольца:

_>>;

нахождение предела “среднего арифметического” первых n значений варианты _>>;

_>>;

_>>.

Применение теоремы Штольца к нахождению некоторых пределов отношения последовательностей.

Нахождение некоторых пределов отношения функций с помощью теоремы Штольца.

Для определения пределов неопределенных выражений _>> типа _>> часто бывает полезна следующая теорема, принадлежащая Штольцу.

Пусть варианта _>>, причем – хотя бы начиная с некоторого листа – с возрастанием n и _>> возрастает: _>>. Тогда _>>=_>>,

Если только существует предел справа (конечный или даже бесконечный).

Допустим, что этот предел равен конечному числу _>>:

_>>.

Тогда по любому заданному _>> найдется такой номер N, что для n>N будет

или

_>>.

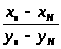Значит, какое бы n>N ни взять, все дроби _>>, _>>, …, _>>, _>>лежат между этими границами. Так как знаменатели их, ввиду возрастания y_>n> вместе с номером n, положительны, то между теми же границами содержится и дробь _>>, числитель которой есть сумма всех числителей, написанных выше дробей, а знаменатель – сумма всех знаменателей. Итак, при n>N

_>>.

Напишем теперь тождество:

_>>,

откуда

_>>.

Второе слагаемое справа при n>N становится <_>>; первое же слагаемое, ввиду того, что _>>, также будет <_>>, скажем, для n>N^’. Если при этом взять N^’>N, то для n>N^’, очевидно, _>>, что и доказывает наше утверждение.

Примеры:

Пусть, например, _>>. Отсюда, прежде всего вытекает, что (для достаточно больших n) _>>, следовательно, вместе с y_>n> и x_>n>, причем варианта x_>n> возрастает с возрастанием номера n. В таком случае, доказанную теорему можно применить к обратному отношению _>>

_>>

(ибо здесь предел уже конечен), откуда и следует, что _>>, что и требовалось доказать.

При а>1

_>>

Этот результат с помощью теоремы Штольца получается сразу:_>>

_>>

Применим теорему Штольца к доказательству следующего интересного предложения:

Если варианта a_>n>_>>имеет предел (конечный или бесконечный), то этот же предел имеет и варианта

_>>

(“среднее арифметическое” первых n значений варианты а_>n>).

Действительно, полагая в теореме Штольца

X_>n>=a_>1>+a_>2>+…+a_>n,>y_>n>=n,

Имеем:

_>>

Например, если мы знаем, что _>>,

то и _>>

Рассмотрим теперь варианту (считая k-натуральным)

_>>,

которая представляет неопределённость вида _>>.

Полагая в теореме Штольца

x_>n>=1^k+2^k+…+n^k, yⁿ=n^k+1,

будем иметь

_>>.

Но

(n-1)^k+1=n^k+1-(k+1)n^k+… ,

так что

n^k+1-(n-1)^k+1=(k+1)n^k+…

_>>.

Определим предел варианты

_>> ,

представляющей в первой форме неопределенность вида _>>, а во второй – вида _>>. Произведя вычитание дробей, получим на этот раз неопределенное выражение вида _>>:

_>>.

Полагая x_>n> равным числителю этой дроби, а y_>n> – знаменателю, применим еще раз ту же теорему. Получим

_>>.

Но _>>,

а _>>,

так что, окончательно,

_>>.

Пример 1.

_>>=_>>=_>>=_>>=_>>=_>>= _>>=_>>_>>=_>>=_>>.

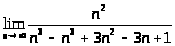Пример 2.

_>>=

=_>>=

=_>>.

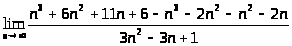Пример 3.

_>>

=_>>

=_>>.

Теорема Штольца справедлива для последовательностей, но т.к. последовательности есть частный случай функций, то эту теорему можно обобщить для функций.

Теорема.

Пусть функция _>>, причем, начиная с некоторой x_>k>, g(x_>k>+1)>g(x_>k>), т.е. функция возрастающая.

Тогда _>>,

если только существует предел справа конечный или бесконечный.

Доказательство:

Допустим, что этот предел равен конечному числу k

_>>.

Тогда, по определению предела _>>

_>>

или

_>>.

Значит, какой бы _>> ни взять, все дроби

_>>, _>>, …, _>>

лежат между этими границами. Так как знаменатели их, ввиду возрастания g(x_>n>) вместе с x(n), положительны, то между теми же границами содержится и дробь _>>, числитель которой есть сумма всех числителей, написанных выше дробей, а знаменатель – сумма всех знаменателей. Итак, при _>>

_>>.

Напишем тождество(которое легко проверить):

_>>,

Откуда

_>>.

Второе слагаемое справа при _>> становится _>>; первое же слагаемое, ввиду того, что _>>, так же будет _>>, скажем, для _>>. Если при этом взять _>>, то для _>>, очевидно _>>, что и доказывает теорему.