Аппроксимация функций (работа 1)

Аппроксимация функций

Из курса математики известны 3 способа задания функциональных зависимостей:

аналитический

графический

табличный

Табличный способ обычно возникает в результате эксперемента.

Недостаток табличного задания функции заключается в том, что найдутся значения переменных которые неопределены таблицей. Для отыскания таких значений определяют приближающуюся к заданной функцию, называемой аппроксмирующей, а действие замены аппроксимацией.

Аппроксимация заключается в том, что используя имеющуюся информацию по f(x) можно рассмотреть другую функцию φ(ч) близкую в некотором смысле к f(x), позволяющую выполнить над ней соответствующие операции и получить оценку погрешность такой замены.

φ(х)- аппроксимирующая функция.

Интерполяция (частный случай аппроксимации)

Если для табличной функции y=f(x), имеющей значение x_>0> f(x_>0>) требуется построить аппроксимирующюю функцию j(x) совпадающую в узлах с x_>i> c заданной, то такой способ называется интерполяцией

При интерполяции, заданная функция f(x) очень часто аппроксимируется с помощью многочлена, имеющего общий вид

j(x)=p_>n>(x)=a_>n>xⁿ+a_>n-1>x^n-1+…+a_>0>

В данном многочлене необходимо найти коэффициенты a_>n>,a_>n-1>, …a_>0> , так как задачей является интерполирование, то определение коэффициентов необходимо выполнить из условия равенства:

P_>n>(x_>i>)=y_>i> i=0,1,…n

Для определения коэффициентов применяют интерполяционные многочлены специального вида, к ним относится и полином Лагранжа L_>n>(x).

_>> i¹j

В точках отличных от узлов интерполяции полином Лагранжа в общем случае не совпадает с заданной функцией .

Задание

С помощью интерполяционного полинома Лагранжа вычислить значение функции y в точке x_>c>, узлы интерполяции расположены равномерно с шагом Dх=4,1 начиная с точки х_>0>=1,3 даны значения функции y={-6.56,-3.77,-1.84,0.1,2.29,4.31,5.86,8.82,11.33,11.27}.

ГСА для данного метода

CLS

DIM Y(9)

DATA -6.56,-3.77,-1.84,0.1,2.29,4.31,5.86,8.82,11.33,11.27

X0 = 1.3: H = 4.1: N = 10: XC = 10

FOR I = 0 TO N - 1

1 X(I) = X0 + H * I

READ Y(I)

PRINT Y(I); X(I)

NEXT I

S1 = 0: S2 = 0: S3 = 0: S4 = 0

FOR I = 0 TO N - 1

2 S1 = S1 + X(I) ^ 2

S2 = S2 + X(I)

S3 = S3 + X(I) * Y(I)

S4 = S4 + Y(I)

NEXT I

D = S1 * N - S2 ^ 2

D1 = S3 * N - S4 * S2

D0 = S1 * S4 - S3 * S2

A1 = D1 / D: A0 = D0 / D

YC = A1 * XC + A0

PRINT "A0="; A0, "A1="; A1, "YC="; YC

FOR X = 0 TO 50 STEP 10

Y = A1 * X + A0

PRINT X, Y

NEXT X

END

XC= 10

Х Y

1.3 -6.56

5.4 -3.77

9.5 -1.84

13.6 .1

17.7 2.29

21.8 4.31

25.9 5.86

30 8.82

34.1 11.33

38.2 11.27

S=-1.594203

АППРОКСИМАЦИЯ ФУНКЦИЕЙ. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ.

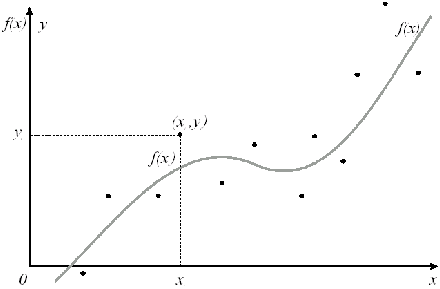
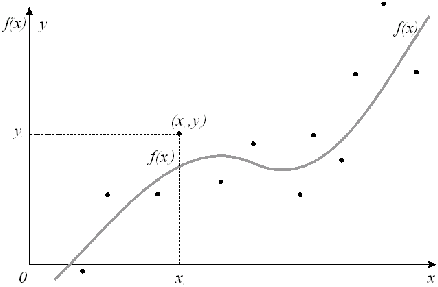
В инженерной деятельности часто возникает необходимость описать в виде функциональной зависимости связь между величинами, заданными таблично или в виде набора точек с координатами (x_>i>,y_>i>), i=0,1,2,...n, где n - общее количество точек. Как правило, эти табличные данные получены экспериментально и имеют погрешности. При аппроксимации желательно получить относительно простую функциональную зависимость (например, полином), которая позволила бы "сгладить" экспериментальные погрешности, получить промежуточные и экстраполяционные значения функций, изначально не содержащиеся в исходной табличной информации.

Графическая интерпретация аппроксимации.

Эта функциональная (аналитическая) зависимость должна с достаточной точностью соответствовать исходной табличной зависимости. Критерием точности или достаточно "хорошего" приближения могут служить несколько условий.

Обозначим через f_>i>_>>значение, вычисленное из функциональной зависимости для x=x_>i>_>>и сопоставляемое с y_>i>.

Одно из условий согласования можно записать как

S = _>>(f_>i>-y_>i>)  min ,

т.е. сумма отклонений табличных и функциональных значений для одинаковых x=x_>i> должна быть минимальной (метод средних). Отклонения могут иметь разные знаки, поэтому достаточная точность в ряде случаев не достигается.

Использование критерия S = |f_>i>-y_>i>|  min , также не приемлемо, т.к. абсолютное значение не имеет производной в точке минимума.

Учитывая вышеизложенное, используют критерий наименьших квадратов, т.е. определяют такую функциональную зависимость, при которой
S = (f_>i>-y_>i>)² , (1)

обращается в минимум.

В качестве функциональной зависимости рассмотрим многочлен

f(x)=C_>0>+_>>C_>1>X+C_>2>X²+...+C_>M>X^M. (2)

Формула (1) примет вид S = _>>( C_>0>+_>>C_>1>X_>i>+C_>2>X_>i>²+...+C_>M>X_>i>^M - Y_>i>) ²

Условия минимума S можно записать, приравнивая нулю частные производные S по независимым переменным С_>0,>С_>1>,...С_>М> :

S_>C0> = 2 ( C_>0>+_>>C_>1>_>>X_>i>+C_>2>_>>X_>i>²+...+C_>M>_>>X_>i>^M - Y_>i>) = 0 ,

S_>C1> = 2 ( C_>0>+_>>C_>1>_>>X_>i>+C_>2>_>>X_>i>²+...+C_>M>_>>X_>i>^M - y_>i>) X_>i> = 0 ,(3)

S_>CM> = 2 ( C_>0>+_>>C_>1>_>>X_>i>+C_>2>_>>X_>i>²+...+C_>M>_>>X_>i>^M - Y_>i>) X_>i>^M = 0 ,

Тогда из (3) можно получить систему нормальных уравнений

C_>0> _>> (N+1) + C_>1>_>>_>>X_>i> +_>>C_>2>_>>X_>i>² +...+ C_>M>_>>_>>X_>i>^M = _>>Y_>i> ,

C_>0>_>>X_>i> +_>>C_>1>_>>X_>i>² +_>>C_>2>_>>X_>i>³ +...+ C_>M>_>>X_>i>^M+1 = _>>Y_>i> X_>i> ,(4)

C_>0>_>>X_>i>^M +_>>C_>1>_>>X_>i>^M+1 +_>>C_>2>_>>X_>i>^M+2 +...+ C_>M>_>>X_>i>^2M =_>> Y_>i> X_>i>^M .

Для определения коэффициентов С_>i> и, следовательно, искомой зависимости (2) необходимо вычислить суммы и решить систему уравнений (4). Матрица системы (4) называется матрицей Грама и является симметричной и положительно определенной. Эти полезные свойства используются при ее решении.

(N+1)	_>>X_>i>	_>>X_>i>²	...	_>>X_>i>^M	_>>Y_>i>
X_>i>	_>>X_>i>²	_>>X_>i>³	...	_>>X_>i>^M+1	Y_>i> X_>i>
...	...	...	...	...	...
X_>i>^M	_>>X_>i>^M+1	_>>X_>i>^M+2	...	_>>X_>i>^2M	_>>Y_>i> X_>i>^M

Нетрудно видеть, что для формирования расширенной матрицы (4а) достаточно вычислить только элементы первой строки и двух последних столбцов, остальные элементы не являются "оригинальными" и заполняются с помощью циклического присвоения.

Задание

Найти коэффициенты прямой и определить значение функции y{-6.56,-3.77, -1.84,0.1,2.29,4.31,5.56,8.82,11.33,11.27}, x0=1.3 h=4.1, и определить интеграл заданной функции.

Программа

¦CLS

¦XC = 10: X0 = 1.3: H = 4.1: N = 10

¦DIM Y(9): DIM X(9)

¦DATA -6.56,-3.77,-1.84,0.1,2.29,4.31,5.86,8.82,11.33,11.27

¦FOR I = 0 TO N - 1

¦X = X0 + H * I:

¦X(I) = X

¦READ Y(I)

¦PRINT X(I), Y(I)

¦NEXT I

¦S1 = 0: S2 = 0: S3 = 0: S4 = 0

¦I = 0

¦10 S1 = S1 + X(I) ^ 2:

¦S2 = S2 + X(I):

¦S3 = S3 + X(I) * Y(I):

¦S4 = S4 + Y(I)

¦I = I + 1

¦IF I <= N - 1 THEN 10

¦D = S1 * N - S2 ^ 2:

¦D1 = S3 * N - S2 * S4:

¦D0 = S1 * S4 - S2 * S3

¦A1 = D1 / D:

¦A0 = D0 / D

¦Y = A1 * XC + A0

¦PRINT TAB(2); "КОЭФФИЦИЕНТ ПРЯМОЙ В ТОЧКЕ A0="; A0,

¦PRINT TAB(2); "КОЭФФИЦИЕНТ ПРЯМОЙ В ТОЧКЕ A1="; A1,

¦PRINT TAB(2); "ЗНАЧЕНИЕ ФУНКЦИИ В ТОЧКЕ XC Y="; Y

¦FOR X = 10 TO 50 STEP 10

¦Y = A1 * X + AO

¦PRINT X, Y

¦NEXT X

¦FOR I = 1 TO N - 1

¦S = S + Y(I): NEXT I

¦D = H / 2 * (Y(0) + Y(N - 1) + 2 * S)

¦PRINT "ЗНАЧЕНИЕ ИНТЕГРАЛА ПО МЕТОДУ ТРАПЕЦИИ D="; D

Ответы

Х Y

1.3 -6.56

5.4 -3.77

9.5 -1.84

13.6 .1

17.7 2.29

21.8 4.31

25.9 5.86

30 8.82

34.1 11.33

38.2 11.27

КОЭФФИЦИЕНТ ПРЯМОЙ В ТОЧКЕ A0=-6.709182

КОЭФФИЦИЕНТ ПРЯМОЙ В ТОЧКЕ A1= .5007687

ЗНАЧЕНИЕ ФУНКЦИИ В ТОЧКЕ XC Y=-1.701495

10 5.007687

20 10.01537

ЗНАЧЕНИЕ ИНТЕГРАЛА ПО МЕТОДУ ТРАПЕЦИИ D= 166.9725