Использование графического метода при изучении электрического резонанса в курсе физики средней школы

Использование графического метода при изучении электрического резонанса в курсе физики средней школы

Цыкун В.Ф., учитель физики сш. №30, г. Хабаровска, Щербаков Н.Г., к.п.н., доцент кафедры общей физики ХГПУ

В настоящее время, когда физические методы исследования проникли во все области науки и техники, особую остроту приобрел вопрос о вооружении учащихся глубокими знаниями и методами исследования в физике.

Одним из методов исследований в физике является графический метод, который дает возможность учащимся усваивать сущность предмета, познавать закономерности новых явлений.

В этой связи является актуальным вопрос использования графического метода преподавания физики, который позволяет наглядно провести всесторонний анализ явления, выявить его причинно-следственные связи и обосновать экспериментальные наблюдения.

В качестве примера рассмотрим применение графического метода при изучении резонанса в электрической цепи.

Так, при изучении в 11 классе темы: «Электрический резонанс», после проведения опыта по наблюдению за яркостью свечения электрической лампочки, активное сопротивление которой , включенной последовательно с катушкой индуктивности , конденсатором и звуковым генератором ЗГ (рис.1), при изменении частоты, для объяснения эксперимента можно использовать графический метод.

С этой целью необходимо дать учащимся следующее задание: исходя из закона Ома для переменного тока постройте зависимость силы тока I от частоты w источника переменного напряжения (I=I(w)).

Учащимся известно, что зависимость силы тока I от напряжения в исследуемой цепи подчиняется закону Ома в следующей форме записи:

,

где - полное сопротивление цепи, которое равно

.

В этом выражении - активное сопротивление контура,

- индуктивное и емкостное сопротивления,

- индуктивность катушки и емкость конденсатора.

Так как напряжение постоянно с изменением частоты, то график зависимости тока от частоты противоположен частотной зависимости сопротивления.

Для построения зависимости от частоты w вначале строятся зависимости (рис.2,3,4)

Затем графики зависимостей представляем на одном рисунке (рис.5). Указанные кривые пересекаются. Точка пересечения этих графиков означает, что при определенном значении частоты источника переменного

тока w емкостное сопротивление конденсатора и индуктивное сопротивления катушки индуктивности равны, т. е. XC=XL или и тогда .

Но учащимся известно, что по формуле рассчитывается собственная частота колебательного контура. Делаем вывод, что при изменении частоты источника переменного тока в колебательном контуре на частоте w = w0 наблюдается равенство реактивных сопротивлений.

С учетом поведения кривых на рис. 5 представлен график модуля реактивного сопротивления цепи . Для его построения необходимо произвести вычитание ординат соответствующих графиков на нескольких частотах. Теперь с учетом рис.2 и 5 качественно можно представить график (рис.6).

Из графика на рис.6 следует, что на частоте и 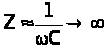(так как ).

Если , то

Для .

С учетом частотной зависимости сопротивления от частоты согласно формуле строится зависимость I=I(w) (рис.7).

График зависимости тока от частоты противоположен графику зависимости полного сопротивления от частоты. На низких () и высоких () частотах , а ; на частоте полное сопротивление цепи для переменного тока является чисто активным и равно , а ток на данной частоте максимален и равен .

Это явление, то есть резкое возрастание тока в цепи на частоте называется электрическим резонансом. Ток, протекающий в цепи через и при последовательном соединении одинаковый, напряжения на индуктивности и емкости находятся в противофазе и генератор на частоте подключен только к . Для объяснения увеличения яркости свечения лампочки на частоте необходимо отметить, что она определяется потребляемой мощностью, которая равна . Поэтому напряжение на резисторе равно напряжению генератора .

Обычно резонансную кривую для последовательной цепи в школьном курсе связывают с кривой I=I(w).

С нашей точки зрения для того, чтобы определить к какому типу относится это явление - резонансу тока или резонансу напряжения, необходимо в дальнейшем сравнить величины напряжений на конденсаторе и катушке индуктивности с напряжением на резисторе на резонансной частоте .

Для этого необходимо рассчитать напряжение на конденсаторе, равное

.

Определив (с помощью омметра) сопротивление цепи , по известной емкости и частоте находят . Расчеты показывают, что на резонансной частоте больше, чем напряжение генератора 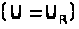. Такое же напряжение будет и на катушке индуктивности.

Вследствие того, что напряжение на катушке индуктивности и конденсаторе во много раз больше напряжения генератора, а также напряжения на резисторе , такой резонанс называется резонансом напряжений.

Исходя из представленных графиков учащиеся делают следующие выводы для явления электрического резонанса для цепи с последовательным соединением и :

а) наблюдается резонанс напряжений ;

б) ток максимален и равен ;

в) полное сопротивление минимально и равно ;

г) емкостное сопротивление равно индуктивному;

д) реактивное сопротивление равно нулю, а значит сдвиг фаз между током и напряжением равен нулю;

с) энергия источника напряжения преобразуется во внутреннюю энергию.

Таким образом использование графического метода позволяет без сложных математических формул рассмотреть на высоком научном уровне такое сложное явление как резонанс напряжений в электрической цепи, состоящей из и элементов при их последовательном соединении, убедиться в закономерностях изучаемого явления, условиях возникновения электрического резонанса, режиме работы источника и колебательного контура на резонансной частоте. При этом бесспорно, нужно учитывать уровень подготовки учащихся (в условиях уровневой дифференциации).

Список литературы

Для подготовки данной применялись материалы сети Интернет из общего доступа