Пределы последовательностей и функций

Пределы последовательностей и функций

Контрольная работа по высшей математике

1. Пределы последовательностей и функций

Числовой последовательностью называется числовая функция, определенная на множестве натуральных чисел. Задать числовую последовательность означает задать закон, по которому можно определить значение любого члена последовательности, зная его порядковый номер п; для этого достаточно знать выражение общего или п-го члена последовательности в виде функции его номера: .

В основе всех положений математического анализа лежит понятие предела числовой последовательности. Число А называется пределом числовой последовательности , если для любого сколь угодно малого положительного числа e существует такой номер , зависящий от выбранного e, начиная с которого все члены последовательности отличаются от А по модулю меньше, чем на e, т. е.

при .

Если последовательность имеет предел А, то она называется сходящейся (к числу А) и этот факт записывают следующим образом:

Пусть функция определена в некоторой окрестности точки . Выберем в некоторой окрестности этой точки какую-нибудь последовательность сходящуюся к точке : . Значения функции в выбранных точках образуют последовательность , и можно ставить вопрос о существовании предела этой последовательности.

Число А называется пределом функции в точке , если для любой сходящейся к последовательности значений аргумента, отличных от , соответствующая последовательность значений функции сходится к числу А, т. е.

Возможно иное определение предела функции в точке: число А называется пределом функции при , если для всякого положительного числа e можно указать другое положительное число d (зависящее от выбора e) такое, что абсолютная величина разности будет меньше e, когда абсолютная величина разности будет меньше , но больше нуля

, если при .

Таким образом, первое определение предела функции основано на понятии предела числовой последовательности, и его называют определением на «языке последовательностей». Второе определение носит название «на языке ».

Кроме понятия предела функции в точке, существует также понятие предела функции при стремлении аргумента к бесконечности: число А называется пределом функции при , если для любого числа существует такое число d, что при всех справедливо неравенство : .

Теоремы о пределах функций являются базой для общих правил нахождения пределов функций. Можно показать, что арифметические операции над функциями, имеющими предел в точке , приводят к функциям, также имеющим предел в этой точке.

Примеры

Найти предел функции

Решение: Имеем неопределенность вида . Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель , который при не равен нулю. В результате неопределенность будет раскрыта.

2. Производная и дифференциал

Пусть функция определена в некоторой окрестности точки .

Производной функции в точке называется предел отношения , когда (если этот предел существует). Производная функции в точке обозначается

Например, выражение следует понимать как производную функции в точке .

Определение производной можно записать в виде формулы

. (4.1)

Предел (4.1) может не существовать. В этом случае говорят, что функция не имеет производной в точке . Если предел (4.1) равен , то говорят, что функция имеет в точке бесконечную производную.

В различных задачах (в том числе и экономических) производная функции интерпретируется как скорость изменения величины y относительно x. Геометрический смысл производной состоит в том, что – это тангенс угла наклона касательной к графику в точке .

Нахождение производной функции называется дифференцированием этой функции. Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке.

Укажем правила дифференцирования, которые сводят вычисление производных одних функций к вычислению производных других (более простых) функций.

Если функции дифференцируемы в точке , то сумма, разность, произведение и частное этих функций также дифференцируемы в точке , и справедливы следующие формулы

Если функция имеет обратную функцию и в точке производная , то обратная функция дифференцируема в точке и или .

Если функция дифференцируема в точке и , то сложная функция также дифференцируема в и верна следующая формула

или .

Пример.

Найти производную функции

Решение:

3 Геометрические изложения и дифференцированные исчисления (построение графиков)

Функция , определенная во всех точках промежутка , называется возрастающей (убывающей) в этом промежутке, если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует большее (меньшее) значение функции, т. е,

если то при

– возрастающая, – убывающая.

Из данного определения вытекает, что для возрастающей функции приращения аргумента и функции имеет один и тот же знак, в силу чего их отношение положительно: . Для убывающей функции эти приращения имеют разные знаки, в силу чего . Те значения аргумента, при которых функция достигает своих наибольших и наименьших по сравнению с близкими значений, называются точками максимума и минимума (точками экстремума).

Точка называется точкой максимума (минимума) непрерывной функции , а значение называется максимумом (минимумом) этой функции, если существует некоторая окрестность точки такая, что значение функции в любой точке этой окрестности будет меньше (больше), чем ее значение в самой точке , т. е. меньше (больше), чем максимум (минимум) (рис. 1).

у max у

min

f(х0) f(х0)

О х0–d х0 х0+d х О х0–d х0 х0+d х

точка максимума

точка минимума

Рис. 1

Из определений точек экстремума следует, что вне d-окрестности точки экстремума поведение функции произвольно, т. е. понятия максимума и минимума функции носят характер локальных (местных), а не абсолютных понятий.

Чтобы установить признаки возрастания и убывания и признаки экстремума функций, рассмотрим ряд важных теорем математического анализа, на которые опираются все дальнейшие исследования функций.

Рекомендуется исследование функций проводить в определенной последовательности.

1. Найти область определения функции; точки разрыва и их характер; вертикальные асимптоты графика.

2. Определить возможный тип симметрии функции (четность, нечетность функции); точки пересечения графика функции с осями координат, т. е. решить уравнения и .

3. Найти наклонные и горизонтальные асимптоты графика функции.

4. Использовать первую производную для определения области возрастания и убывания и экстремумов функции.

5. Использовать вторую производную для определения участков выпуклости и вогнутости графика и точек перегиба.

6. Построить график функции с учетом проведенного исследования.

Пример. Провести полное исследование функции

Решение:

Проведем полное исследование функции, используя следующую схему:

найти область определения функции;

исследовать на четность и нечетность функцию;

найти точки разрыва функции;

найти асимптоты (вертикальные, наклонные и горизонтальные) графика функции;

найти точки пересечения графика функции с координатными осями;

исследовать функцию на монотонность (указав интервалы возрастания и убывания) и экстремум;

определить интервалы выпуклости и вогнутости графика функции, точки перегиба;

при необходимости вычислить значения функции в дополнительных точках;

построить схематично график функции, используя результаты полученные в пунктах 1-8.

Областью определения функции является множество .

Так как и , то функция не является ни четной, ни нечетной.

Функция претерпевает разрыв в точке .

Найдем асимптоты графиков функции:

а). Прямая является вертикальной асимптотой, т.к.

б). Находим наклонные и горизонтальные асимптоты (горизонтальные асимптоты являются частным случаем наклонных асимптот) ,

где ;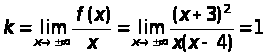

Таким образом, прямая является единственной наклонной асимптотой и на , и на .

Найдем точки пересечения графика функции с осями координат.

а) С осью : , , т.е. точка пересечения с осью - .

б) С осью : , , т.е. точка пересечения с осью - .

6. Исследуем функцию на возрастание, убывание и экстремум. Для этого найдем производную функции.

Из получаем , откуда , .

+ _ +

______________________________________ x

-3 11

Так как на интервалах и производная положительна, т.е. , то график функции на указанных интервалах возрастает. Так как на интервале производная отрицательна, т.е. , то на указанном интервале график функции убывает.

Так как при переходе через точки , производная функции меняет знаки и эти точки входят в область определения функции, то , - точки локального экстремума. Причем точка локального минимума: (так как при переходе через нее производная меняет знак с "+" на "-"); - точка локального максимума: (так как при переходе через нее производная меняет знак с "-" на "+").

7. Исследуем график функции на выпуклость, вогнутость и определим точки перегиба. Для этого найдем вторую производную функции.

Очевидно, что в интервале вторая производная меньше нуля, т.е. , и в этом интервале график функции является выпуклым вверх. В интервале вторая производная больше нуля, т.е. , и в этом интервале график функции является выпуклым вниз (вогнутым).

Несмотря на то, что при переходе через точку вторая производная меняет знак, она не является точкой перегиба, так как не входит в область определения функции, т.е. функция в ней не определена. Таким образом, точек перегиба у графика функции нет.

Из получаем , откуда , .

+ _ +

______________________________________ x

-3 11

4. Неопределенный интеграл

Часто возникает задача, обратная той, которая решалась в дифференциальном исчислении, а именно: дана функция , найти функцию , такую, что .

Функция называется первообразной для данной функции на некотором промежутке Х, если для любого выполняется равенство

Например, пусть , тогда за первообразную можно взять , поскольку .

В основе интегрального исчисления лежит теорема об общем виде первообразной: если – первообразная для функции на промежутке Х, то все первообразные для функции имеют вид , где С – произвольная постоянная.

Выражение вида описывает все первообразные для функции . Действительно, для любой постоянной С

Пусть наряду с данной первообразной функция – также первообразная для . Тогда должны выполняться равенства

откуда . Следовательно, разность этих первообразных будет тождественно равна константе или .

Действие нахождения первообразной называется интегрированием функции.

Доказанная теорема позволяет ввести основное понятие интегрального исчисления: если – первообразная для , то совокупность функций , где С – произвольная постоянная, называется неопределенным интегралом от функции , который обозначается следующим образом

Геометрически неопределенный интеграл представляет собой семейство плоских кривых , называемых интегральными.

Для того, чтобы проверить, правильно ли выполнено интегрирование, надо взять производную от результата и убедиться, что получена подынтегральная функция . Как всякая обратная операция, интегрирование – более сложное действие, чем дифференцирование.

Приведем основные свойства неопределенного интеграла:

1. производная неопределенного интеграла равна подынтегральной функции

;

2. неопределенный интеграл от алгебраической суммы функций равен сумме интегралов от слагаемых функций

;

3. постоянный множитель можно выносить за знак неопределенного интеграла

Значения интегралов от основных элементарных функций получаются из формул дифференцирования этих функций. Приведем таблицу основных интегралов:

1) ;	7) ;
2) ;	8) ;
3) ;	9) ;
4) ;	10)
5) ;	11) ;
6) ;	12) .

Интегралы, содержащиеся в этой таблице, называются табличными.

Пример. Найти неопределенный интеграл. Результат интегрирования проверить дифференцированием

Решение: Для нахождения неопределенных интегралов можно воспользоваться как методом замены переменной, так и методом внесения под знак дифференциала. Покажем оба метода.

1. Воспользуемся методом замены переменной. Введем новую переменную t по формуле . Тогда или . Тогда

После замены переменной воспользовались свойством неопределенного интеграла: постоянный множитель можно выносить за знак неопределенного интеграла, и так как , то пришли к табличному интегралу , где и .

2. Решим этот пример методом внесения под знак дифференциала. Замечая, что и то, что подынтегральное выражение можно представить в виде

внесем под знак дифференциала . Для этого выпишем дифференциал этой функции . Тогда

После внесения под знак дифференциала функции пришли к табличному интегралу , где и .

3. Результат интегрирования проверим дифференцированием. Для этого найдем производную

Таким образом, производная от неопределенного интеграла равна подынтегральной функции, следовательно, интеграл от данной функции найден, верно.

5. Определенный интеграл

Определение определенного интеграла. Пусть функция задана на отрезке [а, b]. Разобьем отрезок [а, b] на п произвольных частей точками

Точки, разделяющие отрезок [а, b] на частичные отрезки длиной , называются точками разбиения. Внутри каждого частичного отрезка выберем произвольную точку . Образуем сумму произведений

называемую интегральной суммой для функции на отрезке [а, b]. Геометрический смысл величины s показан на рис. 2.. Это сумма площадей прямоугольников с основаниями и высотами .

При этом числа a и b называются соответственно нижним и верхним пределами, выражение – подынтегральным выражением, – подынтегральной функцией.

Определенный интеграл численно равен площади криволинейной трапеции, ограниченной вертикальными прямыми при , осью Ох и графиком неотрицательной и непрерывной функции . В этом состоит его геометрический смысл.

Если предположить, что – производительность труда в момент t, то будет численно равен объему произведенной продукции за промежуток , т. е. определенному интегралу можно придать экономический смысл.

Мi

О х0=а хi хi+1 b= хn х

Рис. 2

Предел интегральной суммы при стремлении к нулю, не зависящий от способа выбора точек и точек , называется определенным интегралом от функции на [а, b] и обозначается

Определенный интеграл обладает рядом свойств, аналогичных свойствам неопределенного интеграла:

1) постоянный множитель можно выносить за знак интеграла;

2) интеграл от алгебраической суммы функций равен такой же сумме интегралов от этих функций (свойство линейности).

Кроме того, определенному интегралу присущи свойства, не имеющие аналогов в теории неопределенных интегралов:

3) интеграл от постоянной величины равен этой постоянной, умноженной на длину отрезка интегрирования

;

4) при перемене местами пределов интегрирования интеграл изменяет лишь знак

;

5) интеграл с одинаковыми пределами интегрирования равен нулю

;

6) для любых чисел а, b и c имеет место равенство

Пример. Вычислить определенный интеграл с точностью до двух знаков после запятой

Решение:

Воспользуемся методом замены переменной. Введем новую переменную t по формуле . Тогда или . Осуществим пересчет пределов интегрирования, используя вид замены. Подставим нижний предел интегрирования старой переменной в выражение и найдем нижний предел интегрирования новой переменной . Аналогично, подставляя верхний предел интегрирования старой переменной , найдем верхний предел интегрирования новой переменной . Тогда

6. Функции нескольких переменных, дифференцированных исчислений

До сих пор рассматривались функции одной переменной х. В случае зависимости параметров какого-то процесса или явления от многих факторов вводится понятие функции нескольких переменных.

Пусть каждому набору значений n переменных величин из множества M , называемых независимыми переменными, по какому-либо закону ставится в соответствие некоторое число z, называемое зависимой переменной. Тогда говорят, что задана функция нескольких переменных .

Рис. 3

Функция одной переменной изображается на плоскости в виде линии. В случае двух переменных область определения M функции представляет собой некоторое множество точек на координатной плоскости Оxy и тогда графиком функции является некоторая поверхность (рис. 3).

Приведем примеры функций нескольких переменных.

1. Функция вида , где – постоянные числа, называется линейной или гиперплоскостью -мерном пространстве.

2. Функция вида , где – постоянные числа, называется квадратичной формой от переменных .

При рассмотрении функций в n-мерном пространстве широко используется геометрический язык, хотя буквальное понимание геометрических терминов возможно только при п = 2 и п = 3.

Далее для наглядности будем рассматривать функции двух переменных (), хотя практически все понятия и теоремы, сформулированные для , переносятся на случай . Основные понятия математического анализа, введенные для функции одной переменной, переносятся на случай двух переменных. Так, число А называется пределом функции в точке , если для любого числа можно найти число такое, что для всех точек из d-окрестности точки М выполняется неравенство . Для обозначения предела функции в точке используется символика

Окрестностью точки называется круг, содержащий точку М.

В случае функции двух переменных аргумент может стремиться к предельной точке по различным направлениям на плоскости, поэтому следует говорить о пределах функции в точке вдоль определенных линий.

Функция называется непрерывной в точке , если предел функции в этой точке существует и равен значению функции в этой точке, т. е. . Геометрический смысл непрерывности функции при очевиден: график функции представляет собой в точке непрерывности сплошную поверхность в некоторой окрестности этой точки.

Пример. Найти экстремум функции двух переменных z = x2 + y2, x Î [-20, 20], y Î [-10, 10].

Решение.

Необходимое условие экстремума = 2х = 0, = 2у = 0, откуда координаты стационарной точки (хст, уст) = (0, 0).

Вторые производные А = = 2; В = = 0; С = = 2. Так как AC - B2 = 4 > 0, то в точке (0, 0) локальный минимум.

Значение функции в точке минимума z (0, 0) = 0.

Список литературы

Выгодский М.Я. Справочник по высшей математике. - М.: Джангар, 2000. - 864 с.

Гордон В.А., Шмаркова Л.И. Краткий курс математики / Учебное пособие. – Орёл: ОрёлГТУ, 2000. – 96 с.

Демидович Б.П. Сборник задач и упражнений по математическому анализу: М.: Наука, 1972.

Для подготовки данной применялись материалы сети Интернет из общего доступа