Тезис Гьоделя. Теорема Черча
Тезис Гьоделя. Теорема Черча
Реферат з дисципліни «Теория алгоритмів та представлення знань»
Виконав студент 3-го курсу 36 групи Левицький Е.Г.
Європейський Університет
Уманська філія
Кафедра математики та інформатики
Умань – 2005
Вступ
Введение понятия машины Тьюринга уточняет понятие алгоритма и указывает путь решения какой-то массовой проблемы. Однако машина Тьюринга бывает неприменима к начальной информации (исходному слову алфавита). Та же ситуация повторяется относительно некоторых задач, для решения которых не удается создать машины Тьюринга. Один из первых результатов такого типа получен Черчем в 1936 году. Он касается проблемы распознавания выводимости в математической логике.
1). Аксиоматический метод в математике
заключается в том, что все теоремы данной
теории получаются посредством
формально-логического вывода из
нескольких аксиом, принимаемых в данной
теории без доказательств. Например, в
математической логике описывается
специальный язык формул, позволяющий
любое предложение математической теории
записать в виде вполне определенной
формулы, а процесс логического вывода
из посылки
 следствия
следствия
 может быть описан в виде процесса
формальных преобразований исходной
формулы. Это достигается путем
использования логического исчисления,
в котором указана система допустимых
преобразований, изображающих элементарные
акты логического умозаключения, из
которых складывается любой , сколь
угодно сложный формально-логический
вывод.
может быть описан в виде процесса
формальных преобразований исходной
формулы. Это достигается путем
использования логического исчисления,
в котором указана система допустимых
преобразований, изображающих элементарные
акты логического умозаключения, из
которых складывается любой , сколь
угодно сложный формально-логический
вывод.
Вопрос о логической выводимости следствия
 из посылки
из посылки
 является вопросом о существовании
дедуктивной цепочки, ведущей от формулы
является вопросом о существовании
дедуктивной цепочки, ведущей от формулы
 к формуле
к формуле
 .
В связи с этим возникает проблема
распознавания выводимости: существует
ли для двух формул
.
В связи с этим возникает проблема
распознавания выводимости: существует
ли для двух формул
 и
и
 дедуктивная цепочка, ведущая от
дедуктивная цепочка, ведущая от
 к
к
 или нет. Решение этой проблемы понимается
в смысле вопроса о существовании
алгоритма, дающего ответ при любых
или нет. Решение этой проблемы понимается
в смысле вопроса о существовании
алгоритма, дающего ответ при любых
 и
и
 .
Черчем эта проблема была решена
отрицательно.
.
Черчем эта проблема была решена
отрицательно.
Теорема Черча. Проблема распознавания выводимости алгоритмически неразрешима.
Проблема распознавания самоприменимости. Это вторая проблема, положительное решение которой не найдено до сих пор. Ее суть заключается в следующем. Программу машины Тьюринга можно закодировать каким-либо определенным шифром. На ленте машины можно изобразить ее же собственный шифр, записанный в алфавите машины. Здесь как и в случае обычной программы возможны два случая:
1. машина применима к своему шифру, то есть она перерабатывает этот шифр и после конечного числа тактов останавливается;
2. машина неприменима к своему шифру, то есть машина никогда не переходит в стоп - состояние.
Таким образом, сами машины (или их шифры) разбиваются на два класса: класс самоприменимых и класс несамоприменимых тьюринговых машин. Проблема заключается в следующем как по любому заданному шрифту установить к какому классу относится машина, зашифрованная им: к классу самоприменимых или несамоприменимых.
Теорема 2. Проблема распознавания самоприменимости алгоритмически неразрешима.
3). Проблема эквивалентности слов для ассоциативных исчислений.
Рассмотрим некоторый алфавит
 и множество слов в этом алфавите. Будем
рассматривать преобразования одних
слов в другие с помощью некоторых
допустимых подстановок
и множество слов в этом алфавите. Будем
рассматривать преобразования одних
слов в другие с помощью некоторых
допустимых подстановок
 , где
, где
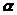 и
и
 два слова в том же алфавите
два слова в том же алфавите
 Если слово
Если слово
 содержит
содержит
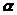 как подслово, например
как подслово, например
 ,
то возможны следующие подстановк
,
то возможны следующие подстановк
 ,
,
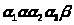 ,
,
 .
.
Ассоциативным исчислением называется совокупность всех слов в некотором алфавите вместе с какой-нибудь конечной системой допустимых подстановок. Для задания ассоциативного исчисления достаточно задать соответствующий алфавит и систему подстановок.
Если слово
 может быть преобразовано в слово
может быть преобразовано в слово
 путем однократного применения определенной
подстановки, то
путем однократного применения определенной
подстановки, то
 и
и
 называются смежными словами.
Последовательность слов
называются смежными словами.
Последовательность слов
 таких, что каждая пара слов
таких, что каждая пара слов
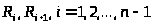 являются смежными, называется дедуктивной
цепочкой, ведущей от слова
являются смежными, называется дедуктивной
цепочкой, ведущей от слова
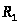 к слову
к слову
 .
Если существует цепочка, ведущая от
слова
.
Если существует цепочка, ведущая от
слова
 к слову
к слову
 ,
то
,
то
 и
и
 называются эквивалентными:
называются эквивалентными:
 ~
~ .
.
Для каждого ассоциативного исчисления возникает своя специальная проблема эквивалентности слов: для любых двух слов в данном исчислении требуется узнать эквивалентны они или нет.
Теорема 3. Проблема эквивалентности слов в любом ассоциативном исчислении алгоритмически неразрешима.
Эта проблема решена лишь в некоторых ассоциативных исчислениях специального вида.
Математические теории.
Аксиоматические теории делятся на формальные и неформальные. Неформальные аксиоматические теории наполнены теоретико – множественным содержанием, понятие выводимости в них довольно расплывчато и в значительной степени опирается на здравый смысл.
Формальная аксиоматическая теория считается определенной, если выполнены следующие условия:
задан язык теории;
определено понятие формулы в этой теории;
выделено множество аксиом теории;
определены правила вывода в этой теории.
Среди математических теорий выделяются теории первого порядка. Эти теории не допускают в своем изложении предикаты, которые имеют в качестве аргументов другие предикаты и функции. Кроме того, не допускаются кванторные операции по предикатам и функциям. Теории первого порядка называются еще элементарными теориями.
1). Язык теории первого порядка. Рассмотрим
некоторый алфавит
 теории
теории
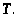 Множество слов
Множество слов
 этого алфавита называется множеством
выражений теории
этого алфавита называется множеством
выражений теории
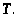 Пару
Пару
 ,
состоящую из алфавита
,
состоящую из алфавита
 и множества выражений,
и множества выражений,
 называют языком теории.
называют языком теории.
В алфавит
 всякой теории
всякой теории
 первого порядка входят:
первого порядка входят:
символы логических операций

символы кванторных операций

вспомогательные символы – скобки и запятые;
конечное или счетное множество
 -
местных предикатных букв;
-
местных предикатных букв;
конечное или счетное множество функциональных букв;
конечное или счетное множество предметных констант.
В частности под функциональной буквой может пониматься цепочка логических операций.
Множество предикатных букв вместе с множеством функциональных букв и констант называется сигнатурой языка данной теории.
Различные теории первого порядка могут отличаться друг от друга по составу букв в алфавите.
Термы и формулы.
В любой теории важное значение имеет определение терма и формулы. Фактически это два класса слов множества.
Термом называется: а). предметная переменная и переменная константа;
Таким образом, кроме предметных переменных и констант термами являются цепочки, образованные из предметных переменных и констант посредством символов операций.
Примеры теорий первого порядка.
1). Геометрия (теория равенства отрезков).
Логические аксиомы этой теории те же
пять, что упомянутые выше. Первичные
термины
 - множество всех отрезков и = - отношение
равенства.
- множество всех отрезков и = - отношение
равенства.
2). Аксиоматическая теория натуральных чисел.
Аксиоматическое построение арифметики
натуральных чисел связано с именами
Пеано и Дедекинда. Язык теории содержит
константу 0, числовые переменные, символ
равенства, функциональные символы +, .
,
 (прибавление
единицы) и логические связки, то есть.
Термы строятся из константы 0 и переменных
с помощью функциональных символов. В
частности натуральные числа изображаются
термами вида 0.
(прибавление
единицы) и логические связки, то есть.
Термы строятся из константы 0 и переменных
с помощью функциональных символов. В
частности натуральные числа изображаются
термами вида 0.
Элементарные формулы в этой теории – это равенства термов, остальные формулы получаются из элементарных с помощью логических связок. Вводится одна предикатная буква и три функциональных буквы.
- отношение равенства, - отношение следования (прибавление единицы), - операция суммы, - операция произведения. В качестве специальных аксиом теории натуральных чисел берутся следующие аксиомы:
где - произвольная формула теории натуральных чисел. Девятая аксиома называется принципом математической индукции. Аксиомы 1-2 обеспечивают очевидные свойства равенства, аксиомы 5-8 уточняют свойства операций сложения и умножения.
Для произвольных теорий первого порядка теорема дедукции, доказанная нами в исчислении высказываний, требует изменения. В первоначальном виде, причем никаких ограничений на предметные переменные, входящие в, не накладывалось. Для справедливости теоремы дедукции для произвольных теорий первого порядка необходимо ее изменить следующим образом.
Теорема Геделя о неполноте. В любой
непротиворечивой формальной системе,
содержащей минимум арифметики, а,
следовательно, и в теории натуральных
чисел, найдется формально неразрешимое
суждение, то есть такая замкнутая формула
 ,
что ни
,
что ни
 ,
ни
,
ни
 не являются выводимыми в системе.
не являются выводимыми в системе.
Пусть у нас есть некая формальная система
T, т.е. некий набор аксиом, из которых мы,
пользуясь фиксированных набором правил
перехода и общелогических аксиом, можем
доказывать какие-нибудь теоремы. Поставим
несколько условий: пусть, во-первых,
наша система T будет сформулирована на
языке арифметики. Это значит, что формулы
аксиом и теорем в T, кроме общелогических
символов (таких, как переменные, скобки,
∧ "и", ¬ "не-" и прочие логические
операции, знак равенства =, а также
кванторы существования ∃ и всеобщности
∀) могут содержать такие символы, как
0 (константа), + (бинарная операция), * (ещё
одна операция), < (отношение "меньше,
чем"), S(x) (функция, обозначающая
"следующий за x элемент", т.е. x+1).
Во-вторых, пусть система T будет достаточно
мощной, что в нашем случае значит, что
она умеет доказывать некоторые достаточно
простые формулы отношений между
натуральными числами (подробности я
опускаю). Например, если мы не внесём
вообще никаких аксиом в T, то она ничего
нетривиального не сможет доказать, т.е.
будет недостаточно мощной и теорема
Гёделя к ней относиться не будет. Но
любой достаточно полный список аксиом
арифметики (например, перечисляющий
обычные тривиальные свойства операций
умножения и сложения, отношения < и
функции S(x)) оказывается достаточно
мощным для наших целей. В-третьих, система
T должна быть в некотором техническом
смысле "легко описываемой" — в ней
должно быть либо конечное количество
аксиом, либо бесконечное, но описываемое
с помощью какого-то заранее известного
алгоритма. Любую формальную систему,
отвечающую этим трём условиям, назовём
подходящей (это не стандартная
терминология, просто для удобства только
в этой записи).
С точки зрения формальных
доказательств система T не имеет
"семантики", иными словами, смысл
используемых в ней символов нам
безразличен. Формальное доказательство
есть всего лишь некоторая длинная
цепочка строк, в которой каждая строка
есть аксиома T, общелогическая аксиома,
или получена из предыдущих строк
применением одного из разрешённых
правил перехода. Мы обозначили, скажем,
одну из операций языка арифметики
символом *, потому что она соответствует
нашему пониманию умножения; но с точки
зрения формальной системы T * — всего
лишь символ, который ничего не означает.
Вместо него мог быть любой другой символ,
скажем, %, и все доказательства оставались
бы в силе; просто если бы мы захотели
определить смысл аксиом или доказываемых
нами теорем, нам пришлось бы понимать
% как "умножение".
Сказать, что какое-то утверждение доказуемо в T — значит сказать, что есть некоторое формальное доказательство, которое к нему приводит. Доказуемость — синтаксическое свойство, а не семантическое. С другой стороны, сказать, что какое-то утверждение истинно — значит, сказать, что если мы интерпретируем его согласно обычной интерпретации символов T (т.е. * будем понимать как "умножение", символ 0 — как число 0, итп.), то получаем истинное утверждение о натуральных числах.
Доказуемость необязательно влечёт
истинность. Предположим для простоты,
что для каждого натурального числа n в
нашем языке есть константа n, позволяющая
"говорить" о числе n в формулах
нашего языка (на практике мы можем
"симулировать" такие константы,
не объявляя их, с помощью цепочки
терминов: 0, S(0), S(S(0)), S(S(S(0))) итп.). Теперь
возьмём формальную систему T, в которой
есть следующая аксиома: 2+2=5. Тогда
утверждение
"2+2=5" доказуемо в
системе T (т.к. оно даже является аксиомой),
но, естественно, ложно (является ложным
утверждением о натуральных числах).
Есть
формальные системы, которые доказывают
только истинные утверждения. Таковы
системы, в которых все аксиомы — истинные
утверждения (можно доказать, что тогда
все правила перехода между аксиомами
сохраняют истинность). Такие формальные
системы называются корректными.
Формальная
система называется консистентной, если
она не может доказать одновременно
какое-то утверждение и его отрицание,
т.е. доказать противоречие. Неконсистентная
формальная система — это плохо и
практически бесполезно, т.к. можно легко
показать, что из доказательства
противоречия можно получить доказательство
чего угодно. Неконсистентная формальная
система доказывает вообще любое
утверждение, так что ничего интересного
в ней нет.
Если система корректна, то
она автоматически консистентна: ведь
она доказывает только истинные
утверждения, а какое-то утверждение и
его отрицание не могут одновременно
быть истинными: одно из них будет
истинным, а другое ложным. Заметим,
однако — это важно! — что "консистентность",
как и "доказуемость" есть свойство
синтаксическое, не зависящее от смысла
формул и их интерпретации; а вот
корректность системы есть свойство
семантическое, требующее понятия
"истинности".
Наконец, формальная
система называется полной, если для
любого утверждения φ
она может доказать либо φ,
либо ¬φ
("не-φ").
Доказательство ¬φ
называется также опровержением φ
; таким образом, полная система может
либо доказать, либо опровергнуть любою
утверждение. В некотором смысле она "на
все вопросы даёт ответ". Что ни скажешь
про натуральные числа — она сможет либо
доказать это, либо опровергнуть. Это
свойство полноты – тоже синтаксическое,
не пользующееся понятием "истинности".
Теперь мы можем определить три формулировки
теоремы Гёделя о неполноте следующим
образом:
1. Пусть T — "подходящая"
(см. выше) формальная система, и предположим
также, что T — корректная система. Тогда
множество утверждений, которые T может
доказать, и множество истинных утверждений
не совпадают (а так как все доказуемые
с помощью T утверждения истинны, отсюда
сразу следует, что есть истинные
утверждения, недоказуемые в T).
2. Пусть
T — "подходящая" формальная система,
и предположим опять, что T корректна.
Тогда мы можем построить конкретное
утверждение G (называемое "гёделевым
утверждением"), обладающее следующим
свойством: G истинно, но недоказуемо в
T.
3. Пусть T — "подходящая" формальная
система, и предположим, что T консистентна.
Тогда T не является полной системой,
т.е. существует утверждение G такое, что
T не может его ни доказать, ни опровергнуть;
более того, мы можем построить такое
конкретное G (называемое "гёделевым
утверждением").
Неполнота системы
T утверждается в качестве результата
только в третьей версии, но легко видеть,
что она сразу следует из заключения и
в первых двух версиях. В них мы заключаем,
что существует какое-то истинное, но
недоказуемое утверждение. Такое
утверждение T не доказывает, но и
опровергнуть его — доказать его отрицание
— она не может, т.к. его отрицание ложно,
а T (в первых двух вариантах теоремы)
корректна и доказывает только истинные
утверждения. Поэтому T не может ни
доказать, ни опровергнуть такое
утверждение G и, следовательно, T
неполна.
Но вот что действительно
отличает первые две версии от третьей:
условие теоремы. В первых двух версиях
от системы T требуется быть корректной;
в третьей версии она должна быть всего
лишь консистентной — намного более
слабое требование. Есть бесчисленное
количество консистентных, но некорректных
систем. Ещё более важен тот факт, что и
в условии, и в заключении третьей версии
теоремы используются только синтаксические
понятия, не требующие понятия "истинности",
не требующие семантики. Третья версия
теоремы и есть та, которую первоначально
доказал Гёдель в начале 30-х годов прошлого
века.
если быть совсем точным,
формулировка Гёделя включала дополнительное
синтаксическое условие для теории T,
называющееся w-консистентностью
(произносится "омега-консистентность").
Однако через пять лет после публикации
статьи Гёделя Россер доказал, что от
этого условия можно избавиться и
достаточно одной консистентности)
То,
что в самой сильной и общей своей
формулировке теорема Гёделя не накладывает
на T никаких существенных семантических
условий, и заключение её тоже вполне
синтаксично — это очень важно понять.
Важно не только и не столько потому, что
иногда мы хотим применить теорему Гёделя
к некорректным системам, хоть и это тоже
верно. Важно в основном по следующим
двум причинам.
Во-первых, первая теорема
о неполноте Гёделя используется в
доказательстве второй теоремы о неполноте
Гёделя, которая доказывает, что
"подходящая" (в несколько другом,
но схожем с описанным выше, смысле)
формальная система T не может доказать
собственную консистентность, если она
консистентна (если она неконсистентна,
то она может доказать всё что угодно,
включая собственную консистентность,
как ни парадоксально это звучит). Я не
буду вдаваться в подробности, но замечу
лишь, что в процессе доказательства
второй теоремы о неполноте необходимо
показать, что доказательство первой
теоремы о неполноте можно формализовать
внутри системы T. Иными словами, не просто
"если T консистента, то она неполна"
(третья версия первой теоремы о неполноте,
см. выше), но также это утверждение
(точнее, его арифметический аналог)
можно доказать в самой системе T. Но в
то время, как можно формализовать
"внутри" системы T такие понятия,
как "формальная система",
"консистентность" и "полнота",
оказывается, что понятие "истинности"
формализовать внутри T невозможно в
принципе. Поэтому первый и второй
варианты теоремы Гёделя, хоть они и
более просты для доказательства, не
могут быть использованы для доказательства
второй теоремы Гёделя.
Во-вторых, теорема Гёделя о неполноте применима не только к формальным системам, сформулированным в языке арифметики (т.е. говорящим о натуральных числах), но также к бесчисленному множеству других формальных систем, от которых требуется только, чтобы они были "подходящими" в нужном техническом смысле; главное требование здесь — чтобы они были не менее мощными, чем теория T в языке арифметики, для которой мы собственно доказываем теорему Гёделя, а это требование обеспечивается возможностью интерпретировать T в такой новой теории. Например, формальная система ZFC, используемая для формализации теории множеств, а вместе с ней и практически всей современной математики, намного более мощна, чем какая-нибудь простенькая арифметическая T, для которой мы доказали теорему Гёделя этот факт можно строго описать (предъявив интерпретацию, т.е. способ перевести утверждения из языка T в утверждения языка ZFC, и показав, что ZFC тогда доказывает "перевод" всех аксиом T) и из него тогда будет следовать, что и ZFC тоже неполна, т.е. в ней тоже есть какое-то гёделево утверждение G, которое нельзя ни доказать, ни опровергнуть.
Проблема, однако, в том, что в отличие от арифметических формальных систем, для утверждений которых у нас всегда есть удобный и обычный способ определить их истинность (посмотреть на то, верны ли они как утверждения о натуральных числах), для других формальных систем, таких, скажем, как ZFC, понятие истинности вообще не определено или определено очень плохо. Для них первая и вторая версии теоремы Гёделя оказываются неподходящими именно потому, что эти версии опираются на корректность данной системы и на существование определённого понятия истинности утверждений. Подходит только третья, чисто синтаксическая версия.
Список литературы
1. www.intuit.ru
2. www.proza.ru
3. www.referat.ru