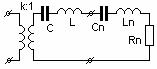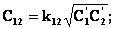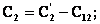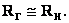Широкополосное согласование комплексных нагрузок на основе теории связанных контуров
Широкополосное согласование комплексных нагрузок на основе теории связанных контуров
к.т.н. В.А. Яковенко
На основе теории одиночных и связанных колебательных контуров разработана методика расчета согласующих цепей простых комплексных нагрузок. Получены соотношения для оценки потенциальных возможностей согласования нагрузок и определения параметров элементов одно- двух- и трехзвенных полиномиальных и оптимальных согласующих цепей при максимально плоской и чебышевской характеристиках рабочего затухания. Полученные расчетные соотношения особенно удобны при расчетах с помощью ЭВМ, так как не требуют ввода в ЭВМ больших массивов чисел, составляющих содержание расчетных таблиц.
Инженерные методики расчета широкополосных согласующих цепей (СЦ) хорошо разработаны особенно для простых типов нагрузок. Как правило, они базируются на табличных зависимостях /1,2/ и позволяют рассчитать отвечающую требованиям практики оптимальную чебышевскую СЦ. При этом, как правило, применяются цепи с количеством звеньев не более трех, так как с дальнейшим увеличением количества звеньев сложности реализации и настройки существенно растут, а потенциальные возможности согласования цепи увеличиваются незначительно. Ниже предлагаются полученные на основе теории одиночных и связанных контуров относительно простые аналитические соотношения, позволяющие произвести оценку потенциальных возможностей согласования комплексной нагрузки и произвести расчет элементов одно-, двух- и трехконтурных полиномиальных и оптимальных СЦ при максимально плоской и чебышевской аппроксимации рабочего затухания цепи.
1. Краткие сведения из теории колебательных систем
Теория колебательных
систем в наиболее полном виде была
разработана в 30-х годах прошлого века
З.И. Моделем /3/ и базируется на нескольких
основополагающих понятиях, среди которых
одним из основных является понятие
резонанса. Различают два типа резонанса
- последовательный (резонанс напряжений)
и параллельный (резонанс токов). Первый
из них наблюдается в последовательной
цепи, состоящей из индуктивности
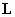 ,
емкости
,
емкости
 и
резистора
и
резистора
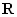 ,
второй - в параллельной цепи из таких
же элементов. Частота
,
второй - в параллельной цепи из таких
же элементов. Частота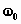 ,
на которой наблюдается резонанс,
определяется величинами входящих в
состав контуров
,
на которой наблюдается резонанс,
определяется величинами входящих в
состав контуров
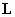 и
и
 ,
не зависит от
,
не зависит от
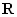 и
равна
и
равна
 Величина
сопротивлений емкости и индуктивности
на резонансной частоте
Величина
сопротивлений емкости и индуктивности
на резонансной частоте
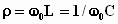 называется
характеристическим сопротивлением
контура. Отношение запасаемай в реактивных
элементах контура к рассеиваемой за
период колебаний резонансной частоты
в его диссипативном (резистивном)
элементе энергий называется добротностью
контура
называется
характеристическим сопротивлением
контура. Отношение запасаемай в реактивных
элементах контура к рассеиваемой за
период колебаний резонансной частоты
в его диссипативном (резистивном)
элементе энергий называется добротностью
контура
 .
Для последовательного контура
.
Для последовательного контура
 ,
для параллельного -
,
для параллельного -

Каноническая структура
системы связанных контуров предполагает
чередование рассмотренных выше двух
типов контуров, связанных между собой
внутри- или внешнеемкостной, внутри-
или внешнеиндуктивной связью. В
предположении отсутствия потерь в
промежуточных контурах, что вполне
оправдано при относительных полосах
пропускания цепи гораздо больших
обратной величины ненагруженной
добротности контура, система связанных
контуров характеризуется следующими
параметрами. Добротность нагрузочного
(последнего от генератора) контура
определяется так же, как и для одиночного
контура. Приведенная добротность
промежуточного контура
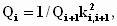 где
где
 -
добротность
-
добротность
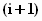 контура;
контура;
 -
коэффициент связи между
-
коэффициент связи между
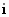 -тым
и
-тым
и
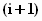 контурами.
Коэффициент связи между контурами
определяется величинами элемента связи
и одноименных элементов взаимно связанных
контуров. При внутриемкостной и
внешнеиндуктивной связях
контурами.
Коэффициент связи между контурами
определяется величинами элемента связи
и одноименных элементов взаимно связанных
контуров. При внутриемкостной и
внешнеиндуктивной связях
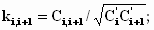

При внутриемкостной и внешнеиндуктивной связях
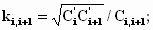
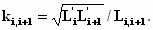
Здесь штрихами помечены
элементы соответствующих парциальных
контуров системы,
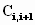 и
и
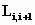 -
элементы связи между
-
элементы связи между
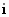 -тым
и
-тым
и
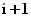 -м
контурами.
-м
контурами.
Парциальным называется контур в составе системы связанных контуров эквивалентный исходному по резонансной частоте и характеристическому сопротивлению. Парциальный контур получается при закорачивании связанных с ним параллельных и размыкании связанных с ним последовательных контуров.
Основной характеристикой
колебательной системы является частотная
характеристика его коэффициента
передачи
 .
Для одноконтурной системы квадрат
модуля коэффициента передачи
.
Для одноконтурной системы квадрат
модуля коэффициента передачи
 (1)
(1)
где
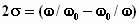 -
относительная расстойка;
-
относительная расстойка;
 -
для последовательного контура и
-
для последовательного контура и
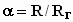 -
для параллельного;
-
для параллельного;
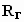 и
и
 -
внутреннее сопротивление и эдс генератора,
а нагрузкой служит резистор контура.
-
внутреннее сопротивление и эдс генератора,
а нагрузкой служит резистор контура.
Для двухконтурной системы
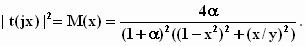 (2)
(2)
Здесь
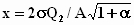 -
обобщенная расстройка;
-
обобщенная расстройка;
 -
обобщенный фактор связи;
-
обобщенный фактор связи;
 -
фактор связи;
-
фактор связи;
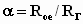 ,
если первый (генераторный) контур
последовательный и
,
если первый (генераторный) контур
последовательный и
 ,
если первый контур параллельный;
,
если первый контур параллельный;
 -
входное сопротивление системы на
резонансной частоте;
-
входное сопротивление системы на
резонансной частоте;
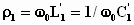 -
характеристическое сопротивление
первого парциального контура;
-
характеристическое сопротивление
первого парциального контура;
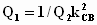 -
приведенная добротность первого контура;
-
приведенная добротность первого контура;
 -
коэффициент связи между контурами.
-
коэффициент связи между контурами.
Для системы трех связанных контуров
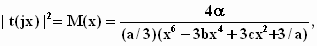 (3)
(3)
Здесь
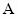 и
и
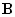 -
факторы связи между первым и вторым,
вторым и третьим контурами соответственно;
-
факторы связи между первым и вторым,
вторым и третьим контурами соответственно;



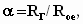 если
первый (Генераторный) контур последовательный
и
если
первый (Генераторный) контур последовательный
и
 если
первый контур последовательный.
если
первый контур последовательный.
Форма частотной
характеристики модуля коэффициента
передачи цепи зависит от степени связи
между контурами системы. Так в двухконтурной
системе при связи меньше критической,
когда
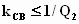 ,
эта зависимость одноэкстремальная
(одногорбая). При связи больше критической,
когда
,
эта зависимость одноэкстремальная
(одногорбая). При связи больше критической,
когда больше
больше
 ,
в частотной характеристике появляется
провал и она приобретает двугорбый
характер. Примечательно, что критической
связи между контурами соответствует
максимально плоская аппроксимация
характеристик цепи, а связи больше
критической - чебышевская аппроксимация.
Это утверждение справедливо при любом
числе контуров цепи.
,
в частотной характеристике появляется
провал и она приобретает двугорбый
характер. Примечательно, что критической
связи между контурами соответствует
максимально плоская аппроксимация
характеристик цепи, а связи больше
критической - чебышевская аппроксимация.
Это утверждение справедливо при любом
числе контуров цепи.
 2.Потенциальные
возможности согласования комплексной
нагрузки
2.Потенциальные
возможности согласования комплексной
нагрузки
Фундаментальная оценка
сверху для качества согласования любой
комплексной нагрузки была получена
Фано /1/ на основании работ Боде /4/
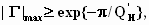 где
где
 -
полосовая добротность нагрузки;
-
полосовая добротность нагрузки;
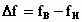 -
полоса согласования;
-
полоса согласования;
 -
средняя частота полосы согласования;
-
средняя частота полосы согласования;
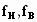 -
нижняя и верхняя частоты полосы
согласования. В практике расчетов СЦ
такая оценка малопригодна, поскольку
она не дает ответа на вопрос о качестве
согласования при конечном числе элементов
цепи.
-
нижняя и верхняя частоты полосы
согласования. В практике расчетов СЦ
такая оценка малопригодна, поскольку
она не дает ответа на вопрос о качестве
согласования при конечном числе элементов
цепи.
Соотношения, связывающие качество согласования с полосовой добротностью нагрузки для конкретного типа и числа элементов СЦ можно получить из выше приведенных выражений для квадрата модуля коэффициента передачи цепи (1)-(3). Рассмотрим это на примере двухзвенных СЦ.
Пусть СЦ состоит из двух связанных контуров (двухзвенная цепь). Тогда

Если полосовая добротность
нагрузки меньше единицы, то расчет СЦ
целесообразно производить на допустимый
в полосе согласования модуль коэффициента
отражения
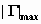 при
при
 (полиномиальная
СЦ). При этом избыток потенциальных
возможностей согласования цепи
используется для улучшения ее фильтрующих
свойств. Поскольку характеристика
(полиномиальная
СЦ). При этом избыток потенциальных
возможностей согласования цепи
используется для улучшения ее фильтрующих
свойств. Поскольку характеристика
 двугорбая
лишь при условии
двугорбая
лишь при условии
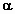 меньше
единицы,
меньше
единицы,
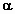 числено
равна коэффициенту бегущей волны КБВ
на входе цепи при
числено
равна коэффициенту бегущей волны КБВ
на входе цепи при

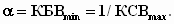 (4)
(4)
Исследуя
 на
экстремум, легко найти
на
экстремум, легко найти
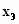 и
и
 (5)
(5)
С другой стороны, для полиномиальной СЦ, как это следует из (2)
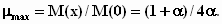 (6)
(6)
Из (5) и (6) с учетом (4)
определим обобщенный фактор связи
 ,
соответствующий заданному качеству
согласования
,
соответствующий заданному качеству
согласования
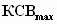 ,
то есть заданному значению
,
то есть заданному значению
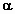
 (7)
(7)
Приравнивая правую часть
(7) выражению для
 из
(2), определим фактор связи
из
(2), определим фактор связи
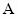 соответствующий
заданному
соответствующий
заданному
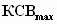
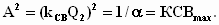 (8)
(8)
Обобщенную расстройку
 ,
соответствующую краю полосы согласования,
определим из условия равенства
,
соответствующую краю полосы согласования,
определим из условия равенства
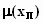 единице
единице
 (9)
(9)
Отсюда, с учетом (7) и
выражения для
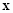 из
(2), получаем требуемую для обеспечения
заданного качества согласования
полосовую добротность нагрузочного
контура
из
(2), получаем требуемую для обеспечения
заданного качества согласования
полосовую добротность нагрузочного
контура
 (10)
(10)
Минимально возможная
величина
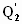 равна
полосовой добротности нагрузки
равна
полосовой добротности нагрузки
 При
этом соотношение (10) является предельным
для двухзвенной полиномиальной
чебышевской СЦ. Из него следует соотношение
При
этом соотношение (10) является предельным
для двухзвенной полиномиальной
чебышевской СЦ. Из него следует соотношение

связывающее качество согласования с добротностью и полосой согласования нагрузки при согласовании ее двухзвенной полиномиальной чебышевской СЦ.
Если полиномиальная цепь
не дает удовлетворительного качества
согласования, что может быть при
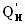 больше
единицы, следует провести оптимизацию
СЦ по критерию минимума
больше
единицы, следует провести оптимизацию
СЦ по критерию минимума
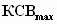 в
заданной полосе согласования. Для этого
следует предположить, что ни на одной
из частот СЦ не обеспечивает идеального
согласования. В этом случае
в
заданной полосе согласования. Для этого
следует предположить, что ни на одной
из частот СЦ не обеспечивает идеального
согласования. В этом случае
 .
(11)
.
(11)
Из (11), (9) и выражений для
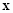 и
и
 из
(2) следует уравнение, связывающее
основные параметры двухзвенной СЦ
из
(2) следует уравнение, связывающее
основные параметры двухзвенной СЦ
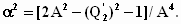 (12)
(12)
Оптимальное значение
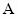 ,
соответствующее максимуму
,
соответствующее максимуму
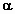 ,
то есть минимуму
,
то есть минимуму
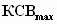 ,
находится приравниванием производной
правой части (12) по
,
находится приравниванием производной
правой части (12) по
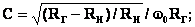 и
равно
и
равно
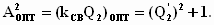 (13)
(13)
Соответствующее
 минимальное
значение
минимальное
значение
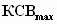 находится
из (12) с учетом (13) и равно
находится
из (12) с учетом (13) и равно
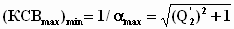 .
(14)
.
(14)
Минимальное значение
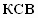 в
полосе согласования при этом определяется
из выражения
в
полосе согласования при этом определяется
из выражения
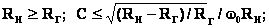
где
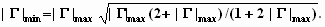
При
 соотношение
(14) является предельным для двухзвенной
оптимизированной чебышевской СЦ. Расчеты
показывают, что оптимизированная таким
образом СЦ является оптимальной в смысле
Боде-Фано.
соотношение
(14) является предельным для двухзвенной
оптимизированной чебышевской СЦ. Расчеты
показывают, что оптимизированная таким
образом СЦ является оптимальной в смысле
Боде-Фано.
Аналогичным образом полученные предельные соотношения для одно-, двух- и трехзвенных полиномиальных и оптимальных СЦ с максимально плоской и чебышевской характеристиками рабочего затухания сведены в табл. 1.
Таблица 1.
|
Тип |
Однозвенная СЦ |
|
Полиномиальная |
|
|
Оптимальная |
|
|
|
Двухзвенная СЦ |
|
Полиномиальная |
Чебышевская |
|
|
Максимально |
|
|
|
Оптимальная |
Чебышевская |
|
|
Максимально |
|
|
|
Трехзвенная СЦ |
|
Полиномиальная |
Чебышевская |
|
|
Максимально |
|
|
|
Оптимальная |
Чебышевская |
|
|
Максимально |
|
С помощью соотношений Табл.1 по известным параметрам нагрузки и заданной полосе согласования можно определить для конкретного типа СЦ предельное значение качества согласования и выбрать подходящую СЦ.
3.Определение параметров элементов СЦ
Основой для расчета параметров элементов СЦ является определения базовых понятий теории колебательных систем - резонансной частоты, добротности, характеристического сопротивления, коэффициента связи между контурами, парциального контура. Расчет начинается с определения требуемых для обеспечения заданных полосы и качества согласования добротности нагрузочного контура и коэффициентов связи между контурами. Методику расчета параметров элементов рассмотрим на примере.
Пусть, к примеру, нагрузка
задана в виде последовательного
соединения
 и
и
 ,
а на предыдущем этапе расчета была
выбрана двухзвенная полиномиальная СЦ
с чебышевской характеристикой рабочего
затухания. Тогда требуемые для обеспечения
заданного качества и полосы согласования
добротность нагрузочного контура
,
а на предыдущем этапе расчета была
выбрана двухзвенная полиномиальная СЦ
с чебышевской характеристикой рабочего
затухания. Тогда требуемые для обеспечения
заданного качества и полосы согласования
добротность нагрузочного контура
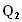 и
коэффициент связи между контурами
и
коэффициент связи между контурами
 определяются
из соотношений
определяются
из соотношений


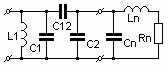
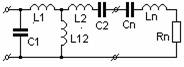
которые следуют непосредственно из (10) и (8). Одна из возможных в этом случае структур СЦ представлена на рис.1. Расчет элементов цепи может быть произведен в следующем порядке.
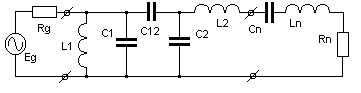
Рис.1. Двухзвенная СЦ с внутриемкостной связью
Имея в виду, что
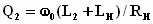 ,
по известным
,
по известным
 и
и
 определяем
определяем
 Индуктивностью
парциального нагрузочного контура
Индуктивностью
парциального нагрузочного контура является сумма
является сумма
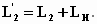 Емкость
парциального нагрузочного контура
Емкость
парциального нагрузочного контура
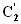 определяется
из условия резонанса парциального
контура на средней частоте полосы
согласования
определяется
из условия резонанса парциального
контура на средней частоте полосы
согласования
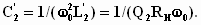 Входное
сопротивление СЦ на резонансной частоте
Входное
сопротивление СЦ на резонансной частоте
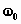 равно
равно

где
 приведенная
добротность и характеристическое
сопротивление первого (генераторного)
контура.
приведенная
добротность и характеристическое
сопротивление первого (генераторного)
контура.
С другой стороны, из
условия заданного значения
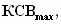 которое
для цепи с четным количеством звеньев
равно всплеску
которое
для цепи с четным количеством звеньев
равно всплеску
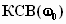 на
средней частоте полосы согласования и
двуволнистости частотной характеристики
цепи
на
средней частоте полосы согласования и
двуволнистости частотной характеристики
цепи
 Отсюда
следует
Отсюда
следует

Поскольку в этом контуре
других индуктивностей нет, а связь между
Контурами емкостная, индуктивность
 является
индуктивностью первого парциального
контура
является
индуктивностью первого парциального
контура
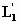 .
Емкость первого парциального контура
.
Емкость первого парциального контура
 определяется
из условия резонанса этого контура на
частоте
определяется
из условия резонанса этого контура на
частоте
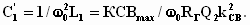
Емкость
 при
выбранной внешнеемкостной связи равна
при
выбранной внешнеемкостной связи равна

При определении емкости второго парциального контура первый (параллельный!) контур следует закоротить. Из получившегося при этом одиночного контура следует

Отсюда по известным
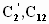 и
и
 определяется
величина емкости
определяется
величина емкости
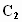

При определении емкости первого парциального контура второй (последовательный!) контур разрывается. Из получившегося при этом одиночного контура следует
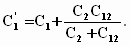
Отсюда по известным
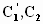 и
и
 находим
находим
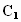

Все параметры элементов СЦ определены.
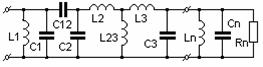
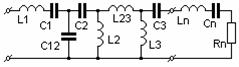
Аналогичным образом определяются параметры элементов СЦ с иным числом звеньев и иных структур. Расчетные формулы для определения параметров элементов некоторых используемых на практике структур СЦ сведены в Табл.2.
Таблица 2.
|
Тип цепи |
N п/п |
Однозвенная СЦ |
||
|
|
Рекомендуется
при
|
|||
|
Квазиполосовая СЦ |
1. |
|
|
|
|
2 |
|
элементов наиболее часто используемых на практике структур СЦ сведены в Табл
|
||
|
3. |
|
|
||
|
4. |
|
|
||
|
Полиномиальная или Оптимальная |
Полиномиальная СЦ:
Оптимальная СЦ:
Идеальный
трансформатор не исключается. СЦ
рекомендуется при
|
|||
|
1. |
|
Полиномиальная СЦ Оптимальная
СЦ |
||
|
2. |
|
Полиномиальная СЦ Оптимальная
СЦ
|
||
|
Тип цепи |
Вид аппроксимации |
Двухзвенная СЦ |
||
|
|
||||
|
Полиномиальная |
Чебышевская |
|
||
|
Максимально плоская |
|
|||
|
Оптимальная |
Максимально плоская |
|
||
|
Чебышевская |
|
|||
|
Полиномиальная или Оптимальная |
1. |
|
|
|
|
2. |
|
|
||
|
3. |
|
|
||
|
4. |
|
|
||
|
Тип цепи |
Вид аппроксимации |
Трехзвенная СЦ |
||
|
|
||||
|
Полиномиальная |
Чебышевская |
|
||
|
Максимально плоская |
|
|||
|
Оптимальная |
Чебышевская |
Рекомендуется взять
Если
по качеству согласования есть
большой запас, то
|
||
|
Максимально плоская |
Рекомендуется взять
Затем из Таб.1определяется
Если
по качеству согласования есть
большой запас, то
|
|||
|
Полиномиальная или Оптимальная |
1. |
|
|
|
|
2. |
|
|
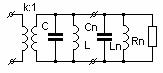
Выбор структуры СЦ определяется структурой и величиной полосовой добротности электрического эквивалента нагрузки. Кроме того, СЦ с одним и тем же количеством звеньев могут различаться между собой видом связей между контурами, которые выбираются из соображений удобства реализации СЦ. При необходимости внутриемкостная связь может быть с помощью известных формул /5/ преобразована во внешнеемкостную и наоборот. Такое преобразование возможно и при индуктивной связи. Все это предопределяет большое разнообразие структур СЦ. Тем не менее, все эти стуктуры поддаются расчету с помощью теории связанных контуров.
4. Краткие итоги работы
Предложен метод решения задачи широкополосного согласования комплексных нагрузок с электрическими эквивалентами первого рода на основе теории колебательных контуров. Получены соотношения для оценки потенциальных возможностей согласования комплексных нагрузок с помощью одно-, двух- и трехзвенных полиномиальных и оптимальных СЦ с чебышевской и максимально плоской характеристиками рабочего затухания. Предложена методика и получены расчетные соотношения для определения параметров элементов некоторых структур указанных выше СЦ. Все расчетные соотношения могут быть использованы при ручных расчетах в процессе разработки радиоэлектронной аппаратуры и особенно удобны при использовании их в машинных методиках расчета.
Список литературы
Фано Р. Теоретические ограничения полосы согласования произвольных импедансов. -М.: Сов. радио, 1965. -68 с.
Алексеев О.В., Животовский А.И., Чавка Г.Г. Широкополосное согласование простых типов нагрузок. Вопросы радиоэлектроники, сер. ТРС, вып.2, 1968.
Модель З.И. Вопросы построения мощных радиостанций. -М.-Л.: ГЭИ, 1947. -206 с.
Боде Г. Теория цепей и проектирование усилителей с обратной связью. -М.: ИЛ, 1948. -641 с.
Чернее Х.И. Индуктивные связи и трансформации в электрических фильтрах. -М.: Связьиздат, 1962. -316 с.


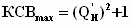
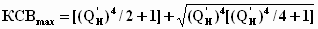



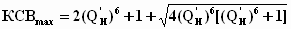
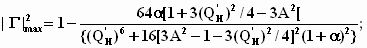
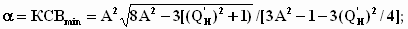




 определяется
как единственный вещественный корень
уравнения
определяется
как единственный вещественный корень
уравнения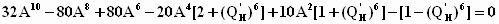
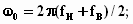
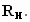











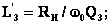



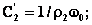 и
и