Центральная предельная теорема и ее доказательство через ряды Тейлора

Прежде чем приступить к рассмотрению центральной предельной теоремы, я считаю нужным сказать о слабой сходимости.

Пусть задана последовательность случайных величин (далее с. в.) , задано некоторое распределение с функцией распределения и — произвольная с. в., имеющая распределение .

Определение.

Говорят, что последовательность с. в. при сходится слабо или по распределению к с. в. и пишут: , или , или ,
если для любого такого, что функция распределения непрерывна в точке , имеет место сходимость при .

Иначе говоря, слабая сходимость — это поточечная сходимость функций распределения во всех точках непрерывности предельной функции распределения.

Свойство 1.

Если , и функция распределения непрерывна в точках и , то

и т.д. (продолжить ряд).

Наоборот, если во всех точках и непрерывности функции распределения имеет место, например, сходимость , то .

Следующее важное свойство уточняет отношения между сходимостями.

Свойство 2.

1. Если , то .

2. Если , то .

Свойство 3.

1. Если и , то .

2. Если и , то .

Несколько содержательных примеров слабой сходимости я рассмотрю ниже. Но основной источник слабо сходящихся последовательностей и необычайно мощное и универсальное средство для асимптотического анализа распределений сумм независимых и одинаково распределенных случайных величин предоставляет нам центральная предельная теорема.

Я буду называть следующее утверждение «ЦПТ Ляпунова» (А. М. Ляпунов: 1901), но сформулирую и докажу теорему Ляпунова только в частном случае, т.е. для последовательности независимых и одинаково распределенных случайных величин.

Центральная предельная теорема.

Пусть — независимые и одинаково распределенные случайные величины с конечной и ненулевой дисперсией: . Обозначим через сумму первых случайных величин: .

Тогда последовательность случайных величин слабо сходится к стандартному нормальному распределению.

Доказательство.

Пусть — последовательность независимых и одинаково распределенных случайных величин с конечной и ненулевой дисперсией. Обозначим через математическое ожидание и через — дисперсию . Требуется доказать, что

Введем стандартизированные случайные величины — независимые с.в. с нулевыми математическими ожиданиями и единичными дисперсиями. Пусть есть их сумма . Требуется доказать, что

Характеристическая функция величины равна

Характеристическую функцию с.в. можно разложить в ряд Тейлора, в коэффициентах которого использовать известные моменты , . Получим

Подставим это разложение, взятое в точке , в равенство и устремим к бесконечности. Еще раз воспользуемся замечательным пределом:

В пределе получили характеристическую функцию стандартного нормального закона. По теореме о непрерывном соответствии можно сделать вывод о слабой сходимости :

распределений стандартизованных сумм к стандартному нормальному распределению, что и утверждается в ЦПТ.

Пользуясь определением и свойствами слабой сходимости, и заметив, что функция распределения любого нормального закона непрерывна всюду на , утверждение ЦПТ можно сформулировать любым из следующих способов:

Следствие.

Пусть — независимые и одинаково распределенные случайные величины с конечной и ненулевой дисперсией. Следующие утверждения эквивалентны друг другу и равносильны утверждению ЦПТ.

Для любых вещественных при имеет место сходимость

Если — произвольная с. в. со стандартным нормальным распределением, то

Следствием из ЦПТ является предельная теорема Муавра-Лапласа.

Предельная теорема Муавра — Лапласа.

Пусть — событие, которое может произойти в любом из независимых испытаний с одной и той же вероятностью . Пусть — число осуществлений события в испытаниях. Тогда .

Иначе говоря, для любых вещественных при имеет место сходимость

Доказательство.

По-прежнему есть сумма независимых, одинаково распределенных с. в., имеющих распределение Бернулли с параметром, равным вероятности успеха :

Осталось воспользоваться ЦПТ.

Ниже я рассмотрю примеры использования ЦПТ.

Пример 1.

З а д а ч а. Монета подбрасывается 10000 раз. Оценить вероятность того, что частота выпадения герба отличается от вероятности более чем на одну сотую.

Р е ш е н и е. Требуется найти , где , 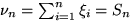— число выпадений герба, а — независимые с. в., имеющие одно и то же распределение Бернулли с параметром 1/2. Домножим обе части неравенства под знаком вероятности на и поделим на корень из дисперсии одного слагаемого.

Согласно ЦПТ или предельной теореме Муавра — Лапласа, последовательность

слабо сходится к стандартному нормальному распределению. Рассмотрим произвольную с. в. , имеющую распределение .

Пример 2.

Прекрасным примером ЦПТ в экономике может служить ее использование в страховом деле. В большинстве случаев конкретный вид распределения потерь (размеров отдельных требований о выплате страховых сумм) не играет существенной роли, поскольку сумма исков, предъявляемых страховщику (величина суммарного иска), обычно зависит только от средней величины и дисперсии убытка. Дело в том, что если количество страховых случаев значительно превышает единицу, то в силу центральной предельной теоремы распределение суммарного иска является нормальным распределением. Обозначив его дисперсию как D_>Z>, а математическое ожидание (среднее значение суммарного иска) как <Z> = <N><Q>

- где <N>, <Q> - среднее значение числа страховых случаев и величины страховой выплаты, получаем следующее выражение для рисковой надбавки Т_>r>:

Т_>r> = [(Т_>0>)/(<N><Q>)](<N>D_>Q> + <Q>²D_>N>)^0.5

- где D_>Q> и D_>N> -дисперсии величины страховой выплаты и количества страховых случаев.

В простейшем случае, когда все выплаты одинаковы (а, следовательно, их дисперсия равна нулю), имеем:

Т_>r> = (Т_>0>)/N^0.5

Эта формула также дает неплохое приближение, если коэффициент вариации уровня страховых выплат значительно меньше единицы.

При включении в страховой полис нескольких независимых рисков ожидаемая величина страховых выплат в соответствии с теоремой о сложении вероятностей представляет собой сумму ожидаемых страховых выплат по каждому риску в отдельности, а рисковая надбавка вычисляется как среднеквадратичная величина всех рисковых надбавок.