Синтез оптимальных уравнений

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Механико-математический факультет

Кафедра теоретической механики и робототехники

Курсовая работа

Тема: Синтез оптимальных уравнений

Студента 3-го курса 13 группы

Павловского Сергея Александровича

Научный руководитель

Лютов Алексей Иванович

Минск 2001г.

ОГЛАВЛЕНИЕ

Г л а в а I. Введение 2

§ 1. Задача об оптимальном быстродействии 2

1.Понятие об оптимальном быстродействии 2

2.Задача управления 3

3.Уравнения движения объекта 5

4.Допустимые управления 6

§ 2. Об основных направлениях в теории оптимальных процессов 7

5.Метод динамического программирования 7

6.Принцип максимума 9

§ 3. Пример. Задача синтеза 12

7.Пример применения принципа максимума 12

8.Проблема синтеза оптимальных управлений 14

Г л а в а II. Линейные оптимальные быстродействия 15

§ 4 Линейная задача оптимального управления 15

9.Формулировка задачи 15

10.Принцип максимума 16

11.Принцип максимума — необходимое и достаточное условие

оптимальности 17

12.Основные теоремы о линейных оптимальных быстродействиях 18

§ 5. Решение задачи синтеза для линейных задач второго порядка 18

13.Упрощение уравнений линейного управляемого объекта 18

Г л а в а III. Синтез оптимальных управлений для уравнения второго

порядка 20

§ 6. Решение задачи синтеза в случае комплексных собственных значений 20

14.Задача синтеза для малых колебаний маятника 20

Список используемой литературы 23

Г л а в а I

ВВЕДЕНИЕ

Управляемые объекты прочно вошли в нашу повседневную жизнь и стали обиходными, обыденными явлениями. Мы видим их буквально на каждом шагу: автомобиль, самолёт, всевозможные электроприборы, снабжённые регуляторами (например, электрохолодильник), и т. п. Общим во всех этих случаях является то, что мы можем «управлять» объектом, можем в той или иной степени влиять на его поведение.

Обычно переход управляемого объекта из одного состояния в другое может быть осуществлён многими различными способами. Поэтому возникает вопрос о выборе такого пути, который с некоторой (но вполне определённой) точки зрения окажется наиболее выгодным. Это и есть (несколько расплывчато сформулированная) задача об оптимальном управлении.

§ 1. Задача об оптимальном быстродействии

Понятие об управляемых объектах. Рассмотрим прямолинейное движение автомобиля. В каждый момент вре­мени состояние автомобиля можно характеризовать двумя числами: пройден­ным расстоянием s и скоростью движения v. Эти две величины меняются с те­чением времени, но не самопроизвольно, а сообразно воле водителя, который может по своему желанию управлять работой двигателя, увеличивая или уменьшая развиваемую этим двигателем силу F. Таким образом, мы имеем три связанных между собой параметра: s, v, F, показанных на схеме (рис. 1). Величины s, v, характеризующие состояние автомобиля, называют его фазовыми координатами, а величину F – управляющим параметром.

Если мы будем рассматривать движение автомобиля по плоскости (а не по прямой), то фазовых координат будет четыре (две «географические» координаты и две компоненты скорости), а управляющих параметров – два (например, сила тяги двигателя и угол поворота руля). У летящего самолёта можно рассматривать шесть фазовых координат (три пространственные координаты и три компоненты скорости) и несколько управляющих параметров (тяга двигателя, величины, характеризующие положение рулей высоты и направления, элеронов).

Разумеется, в проводимом ниже математическом исследовании мы будем иметь дело не с самими реальными объектами, а с некоторой математической моделью. Сказанное выше делает естественным следующее математическое описание управляемого объекта. Состояние объекта задаётся (в каждый момент времени) n числами x¹, x²,…,xⁿ, которые называются фазовыми координатами объекта. Движение объекта заключается с математической точки зрения в том, что его состояние с течением времени изменяется, т. е. x¹,x²,…,xⁿ являются переменными величинами (функциями времени). Движение объекта происходит не самопроизвольно. Им можно управлять; для этого объект снабжён «рулями», положение которых характеризуется (в каждый момент времени) r числами u¹,u²,…,u^r; эти числа называются управляющими параметрами. Рулями можно «манипулировать», т. е. по своему желанию менять (конечно, в допустимых пределах) управляющие параметры u¹,u²,…,u^r. Иначе говоря, мы можем по желанию выбрать функции u¹(t),u²(t),…,u^r(t), описывающие изменение управляющих параметров с течением времени. Мы будем предполагать (как это обычно и бывает), что, зная фазовое состояние объекта в начальный момент времени и выбрав управляющие функции u¹(t),u²(t),…,u^r(t) (для t>t_>0>), мы можем точно и однозначно рассчитать поведение объекта для всех t>t_>0>,_> >т. е. можем найти функции x¹(t),x²(t),…,xⁿ(t), характеризующие изменение фазовых координат с течением времени. Таким образом, изменение фазовых координат x¹,x²,…,xⁿ уже не зависит непосредственно от нашего желания, но на движение объекта мы всё же можем в той или иной мере воздействовать, выбирая по своему желанию управляющие функции u¹(t),u²(t),…,u^r(t).

Управляемый объект, о котором только что шла речь, в теории автоматического управления принято изображать так, как это показано на рис. 2. Величины u¹,u²,…,u^r (управляющие параметры) часто называют также «входными переменными», а величины x¹, x²,…,xⁿ (фазовые координаты) – «выходными переменными». Говорят ещё, что «на вход» объекта поданы величины u¹,u²,…,u^r, а «на выходе» мы получаем величины x¹, x²,…,xⁿ. Разумеется, на рис. 2 показано лишь условное обозначение управляемого объекта и никак не отражено его «внутреннее устройство», знание которого необходимо, чтобы выяснить, каким образом, зная управляющие функции u¹(t),u²(t),…,u^r(t), можно вычислить изменение фазовых координат x¹(t),x²(t),…,xⁿ(t).

Величины u¹,u²,…,u^r удобно считать координатами некоторого вектора u=(u¹,u²,…,u^r), также называемого управляющим параметром (векторным). Точно так же величины x¹, x²,…,xⁿ удобно рассматривать как координаты некоторого вектора (или точки) x=(x¹, x²,…,xⁿ) в n – мерном пространстве с координатами x¹, x²,…,xⁿ. Эту точку называют фазовым состоянием объекта, а n – мерное пространство, в котором в виде точек изображаются фазовые состояния, называется фазовым пространством рассматриваемого объекта. Если объект таков, что его фазовое состояние характеризуется только двумя фазовыми координатами x¹, x² (см. рис. 1), то мы будем говорить о фазовой плоскости. В этом случае фазовые состояния объекта изображаются особенно наглядно.

Итак, в векторных обозначениях рассматриваемый управляемый объект можно изобразить так, как показано на рис. 3. Входящая величина u=(u¹,u²,…,u^r) представляет собой управляющий параметр, а выходная величина x=(x¹, x²,…,xⁿ) представляет собой точку фазового пространства (или, иначе, фазовое состояние объекта).

Как сказано выше, чтобы полностью задать движение объекта, надо задать его фазовое состояние x_>0>=(x_>0>¹, x_>0>²,…, x_>0>ⁿ) в начальный момент времени t_>0> и выбрать управляющие функции u¹(t), u²(t),…, u^r(t) (для t>t_>0>), т. е. выбрать векторную функцию u(t)= u¹(t),u²(t),…,u^r(t)). Эту функцию u(t) мы будем называть управлением. Задание начального фазового состояния x_>0> и управления u(t) однозначно определяет дальнейшее движение объекта. Это движение заключается в том, что фазовая точка x(t)=(x¹(t),x²(t),…,xⁿ(t)), изображающая состояние объекта, с течением времени перемещается, описывая в фазовом пространстве некоторую линию, называемую фазовой траекторией рассматриваемого движение объекта (случай n=2 изображён на рис. 4). Очевидно, что эта линия исходит из точки x_>0>, поскольку x(t_>0>)= x_>0>.

Пару векторных функций (u(t), x(t)), т. е. управление u(t) и соответствующую фазовую траекторию x(t), мы будем называть в дальнейшем процессом управления или просто процессом.

Итак, резюмируем. Состояние управляемого объекта в каждый момент времени характеризуется фазовой точкой x=(x¹, x²,…,xⁿ). На движение объекта можно воздействовать при помощи управляющего параметра u=(u¹,u²,…,u^r). Изменение величин u, x с течением времени мы называем процессом; процесс (u(t), x(t)) составляется из управления u(t) и фазовой траектории x(t). Процесс полностью определяется, если задано управление u(t) (при t>t_>0>) и начальное фазовое состояние x_>0>=x(t_>0>).

Задача управления. Часто встречается следующая задача, связанная с управляемыми объектами. В начальный момент времени t_>0> объект находится в фазовом состоянии x_>0>; требуется выбрать такое управление u(t), которое переведёт объект в заранее заданное конечное фазовое состояние x_>1> (отличное от x_>0>; рис. 5). При этом нередко бывает, что начальное состояние x_>0> заранее не известно. Рассмотрим один из наиболее типичных примеров. Объект должен устойчиво работать в некотором режиме (т. е. находиться в некотором фазовом состоянии x_>1>). В результате тех или иных причин (например, под воздействием неожиданного толчка) объект может выйти из рабочего состояния x_>1> и оказаться в некотором другом состоянии x_>0>. При этом точка x_>0>, в которую может попасть объект, заранее не известна, и мы должны уметь так управлять объектом, чтобы из любой точки x_>0> (или хотя бы из точек x_>0> достаточно близких к x_>1>) вернуть его в рабочее состояние x_>1> (рис. 6).

Такое управление часто осуществляется человеком (оператором), который следит за приборами и старается выбирать управление, поддерживающее объект в требуемом рабочем режиме.

Однако в современных условиях высокого развития техники оператор зачастую не может успешно справиться с этой задачей ввиду сложности поведения объекта, большой быстроты протекания процессов и т. п. Поэтому чрезвычайно важно создать такие приборы, которые сами, без участия человека, управляли бы работой объекта (например, в случае выхода объекта из рабочего состояния возвращали бы его в это рабочее состояние). Такие приборы («регуляторы», «автоматические управляющие устройства» и т. п.) сейчас очень распространены в технике, их изучением занимается теория автоматического управления.

Первым устройством этого рода был центробежный регулятор Уатта, сконструированный для управления работой паровой машины (см. рис. 9). Схема этого регулятора показана на рис. 7. В общем случае (рис. 8) на вход регулятора подаются фазовые координаты объекта.

Обычно требуется, чтобы переходный процесс (т. е. процесс перехода из начального фазового состояния x_>0> в предписанное состояние x_>1>, рис. 5) был в определённом смысле «наилучшим», например, чтобы время перехода было наименьшим или чтобы энергия, затраченная в течение переходного процесса, была минимальной и т. п. Такой «наилучший» переходный процесс называется оптимальным процессом. Термин «оптимальный процесс» требует уточнения, т. к. необходимо разъяснить, в каком смысле понимается оптимальность. Если речь идёт о наименьшем времени перехода, то такие процессы называются оптимальными в смысле быстродействия. Иначе говоря, процесс, в результате которого объект переходит из точки x_>0> в точку x_>1> (рис. 5), называется оптимальным в смысле быстродействия, если не существует процесса, переводящего объект из x_>0> в x_>1> за меньшее время (здесь и далее предполагается, что x_>1>≠ x_>0>). Разумеется, желательно, чтобы регулятор не просто возвращал объект в рабочее состояние, а делал это наилучшим образом, например, в смысле быстродействия (т. е. возвращал объект в рабочее состояние за кратчайшее время). В связи с этим в теории автоматического управления рассматриваются весьма различные регуляторы. Рассмотрение регуляторов приводит к тому, что уменьшение времени переходного процесса связано с усложнением конструкции регулятора; поэтому, усложняя конструкцию регулятора, можно лишь приближаться к «идеальному», «оптимальному» регулятору, который во всех случаях осуществляет переходный процесс за кратчайшее время. В точности же «оптимального» регулятора, по-видимому, осуществить нельзя. Однако такой вывод является ошибочным, т. к. сейчас уже создали математический аппарат, рассчитывающий такие регуляторы. Можно предполагать, что оптимальные регуляторы будут играть важную роль в технике будущего.

Уравнения движения объекта. Начнём с рассмотрения одного простого примера. Пусть G – тело, которое может совершать прямолинейное движение (рис. 10). Массу этого тела будем предполагать постоянной и равной m, а его размерами будем пренебрегать (т. е. будем считать G материальной точкой.) Координату тела G (отсчитываемую от некоторой точки O той прямой, по которой оно движется) будем обозначать через x¹. При движении тела G его координата x¹ меняется с течением времени. Производная представляет собой скорость движения тела G. Будем предполагать, что на тело G действуют две внешние силы: сила трения ─и упругая сила ─ kx¹ и что, кроме того, тело G снабжено двигателем. Развиваемую двигателем силу воздействия на тело G обозначим через u. Таким образом, по второму закону Ньютона движение тела G с течением времени будет описываться дифференциальным уравнением

Обозначив скорость движения через x² (т. е. положив ), мы сможем записать этот закон движения в виде следующей системы дифференциальных уравнений:

(1.1)

Здесь величины x¹, x² являются фазовыми координатами тела G, а величина u – управляющим параметром, т. е. мы имеем объект, схематически изображённый на рис. 11.

Уравнения (1.1) представляют собой закон изменения фазовых координат с течением времени (с учётом воздействия управляющего параметра), т. е. представляют собой закон движения фазовой точки в фазовой плоскости.

Мы рассмотрели лишь один частный случай, но можно было бы указать целый ряд других примеров, в которых закон движения объекта описывается дифференциальными уравнениями. Чаще всего (см.(1.1)) эти уравнения дают выражения производных от фазовых координат через сами фазовые координаты и управляющие параметры, т. е. имеют вид

(1.2)

где f¹, f²,…, fⁿ – некоторые функции, определяемые внутренним устройством объекта.

В дальнейшем мы сосредоточим своё внимание именно на таких объектах (рис. 2), закон движения которых описывается системой дифференциальных уравнений вида (1.2). В векторной форме систему (1.2) можно записать в виде

(1.3)

где x ─ вектор с координатами x¹,…, xⁿ, u – вектор с координатами u¹,…, u^r и, наконец, f(x, u) – вектор, координатами которого служат правые части системы (1.2).

Разумеется, невозможно решить систему дифференциальных уравнений (1.2) (т. е. найти закон движения объекта), не зная каким образом будут меняться с течением времени управляющие параметры u¹, u²,…, u^r. Напротив, зная поведение величин u¹, u²,…,u^r, т. е. зная управляющие функции u¹(t), u²(t),…, u^r(t) для t>t_>0> мы сможем из системы уравнений

(1.4)

или, что то же самое, из векторного уравнения

(1.5)

однозначно определить движение объекта (при t>t_>0>), если нам известно начальное фазовое состояние объекта (в момент t=t_>0>). Иначе говоря, задание управления u(t) и начального фазового состояния x_>0> однозначно определяет фазовую траекторию x(t) при t>t_>0>, что согласуется со сделанными ранее (стр. 1) предположениями о свойствах объекта.

Тот факт, что задание начального фазового состояния (в момент t=t_>0>) позволяет из системы (1.4) однозначно определить фазовую траекторию x(t), t>t_>0>, вытекает из теоремы о существовании и единственности решений системы дифференциальных уравнений. Предположим, что, зная начальное фазовое состояние x_>0> и управление u(t)=(u¹(t),…, u^r(t)), мы определили фазовую траекторию x(t) (с помощью системы (1.4)). Если мы изменим управление u(t) (сохранив то же начальное состояние x_>0>), то получим некоторую другую траекторию, исходящую из той же точки x_>0>; вновь изменим управление u(t) – получим ещё одну траекторию и т. д. Таким образом, рассматривая различные управления u(t), мы получим много траекторий, исходящих из точки x_>0> (рис. 12). (Разумеется, это не противоречит теореме единственности в теории дифференциальных уравнений, так как, заменяя функции u¹(t),…,u^r(t) другими функциями, мы переходим от системы дифференциальных уравнений относительно фазовых координат x¹,…, xⁿ.)

Напомним, что задача оптимального быстродействия заключается в отыскании такого управления u(t), для которого фазовая траектория x(t), соответствующая этому управлению в силу уравнения (1.5), проходит через точку x_>1> и переход из x_>0> в x_>1> осуществляется за кратчайшее время. Такое управление u(t) будем называть оптимальным управлением (в смысле быстродействия); точно так же соответствующую траекторию x(t) буде называть оптимальной траекторией.

Допустимые управления. Обычно управляющие параметры u¹,…,u^r не могут принимать совершенно произвольные значения, а подчинены некоторым ограничениям. Так, например, в случае объекта, описанного на стр. 4, естественно предположить, что сила u, развиваемая двигателем, не может быть как угодно большой по величине, а подчинена ограничениям α≤u≤β, где α и β – некоторые постоянные, характеризующие двигатель. В частности, при α=─1, β=1 мы получаем ограничение ─1≤u≤1, которое означает, что двигатель может развивать силу, направленную вдоль оси x¹ как в положительном, так и в отрицательном направлении, но не превосходящую единицы по абсолютной величине.

Для объектов, содержащих r управляющих параметров u¹,…,u^r, в приложениях часто встречается случай, когда эти параметры могут произвольно меняться в следующих пределах:

α¹≤u¹≤ β¹, α²≤u²≤β²,…, α^r≤u^r≤β^r.

Иначе говоря, каждая из величин u¹, u²,…,u^r в уравнениях (1.2) представляет собой отдельный управляющий параметр, область изменения которого не зависит от значений остальных

управляющих параметров и задаётся неравенствами

αⁱ≤uⁱ≤βⁱ, i=1,…,r. (1.6)

Заметим, что при r=2 точки u=(u¹, u²), координаты которых подчинены неравенствам (1.6), заполняют прямоугольник; при r=3 неравенства (1.6) определяют в пространстве переменных u¹,u²,u³ прямоугольный параллелепипед; в случае произвольного r говорят, что неравенства (1.6) определяют r-мерный параллелепипед.

В общем случае будем считать, что в соответствии с конструкцией объекта и условиями его эксплуатации задано в пространстве переменных u¹,…, u^r некоторое множество U и управляющие параметры u¹, u²,…, u^r должны в каждый момент времени принимать лишь такие значения, чтобы точка u=(u¹,u²,…,u^r) принадлежала множеству U. Иначе говоря, разрешается рассматривать лишь такие управления u(t), что u(t) U для любого t. Множество U в дальнейшем будем называть областью управления. Область управления U не всегда будет параллелепипедом; она может иметь геометрически более или менее сложный характер, так как в силу конструкции объекта между управляющими параметрами u¹, u²,…,u^r могут существовать связи, выражаемые, например, уравнениями вида φ(u¹, u²,…, u^r)=0 или неравенствами ψ(u¹, u²,…, u^r)≤0. Так, если параметры u¹,u² характеризуют векторную величину на плоскости, модуль которой не превосходит единицы, а направление произвольно, то эти параметры подчинены только одному условию

(u¹)² +(u²)² ─1≤0 (1.7)

и область управления U представляет собой круг. В дальнейшем будем предполагать, что указание области управления входит в математическое определение объекта, т. е. что для математического задания управляемого объекта надо указать закон его движения (1.2) и область управления U.

Наконец, сделаем ещё одно, весьма существенное предположение о характере управлений. Именно, будем предполагать, что «рули», положения которых характеризуются управляющими параметрами u¹,u²,…,u^r, безынерционны, так что мы можем, если нужно, мгновенно переключать эти «рули» из одного положения в другое, т. е. менять скачком значения управляющих параметров u¹,u²,…,u^r. В соответствии с этим будем рассматривать не только непрерывные, но и кусочно-непрерывные управления u(t). Кроме того, будем предполагать, что каждое рассматриваемое управление u(t) непрерывно на концах отрезка t_>0>≤t≤t_>1>, на котором оно задано, т. е. что все точки разрыва, если они есть, расположены на интервале t_>0><t<t_>1>. Для удобства условимся называть допустимым управлением всякую кусочно-непрерывную функцию u(t), t_>0>≤t≤t_>1>, со значениями в области управления U, непрерывную справа в точках разрыва (для определённости нам так удобно предполагать) и непрерывную в концах отрезка [t_>0>; t_>1>], на котором она задана.

Задача об оптимальных быстродействиях уточняется теперь следующим образом:

Среди всех допустимых управлений u=u(t), под воздействием которых управляемый объект (1.3) переходит из заданного начального фазового состояния x_>0 >в предписанное конечное состояние x_>1>, найти такое, для которого этот переход осуществляется за кратчайшее время

§ 2. Об основных направлениях в теории оптимальных процессов

Метод динамического программирования. Для управляемого объекта, описанного в предыдущем параграфе, мы рассмотрим задачу об оптимальном переходе ─ в смысле быстродействия ─ из фазового состояния x в фазовое состояние x_>1>. При этом конечную фазовую точку x_>1> будем считать фиксированной, а в качестве начальной точки x будем рассматривать различные точки фазового пространства. Мы будем предполагать в этом пункте, что для рассматриваемого управляемого объекта выполняется следующая гипотеза:

Г и п о т е з а 1. Какова бы ни была отличная от x_>1> точка x фазового пространства, существует оптимальный (в смысле быстродействия) процесс перехода из точки x_>0> в точку x_>1> (рис. 6).

Время, в течение которого осуществляется оптимальный переход из точки x_>0> в точку x_>1>, обозначим через T(x). В дальнейших рассуждениях будет удобно вместо T(x) ввести функцию ω(x), отличающуюся от неё знаком

ω(x)= ─T(x). (1.8)

Так как каждая точка x фазового пространства имеет координаты x¹,…,xⁿ, то ω(x)= ─T(x) является функцией от n переменных, т. е. ω(x)= ω(x¹,…,xⁿ). Поэтому имеет смысл говорить о непрерывности этой функции (по совокупности переменных x¹,…,xⁿ) и о дифференцируемости этой функции по каждой из переменных x¹,…,xⁿ.

А также будем предполагать, что для рассматриваемого управляемого объекта выполняется следующая гипотеза:

Г и п о т е з а 2. Функция ω(x) непрерывна и всюду, кроме точки x_>1>, имеет непрерывные частные производные

Пусть теперь x_>0> ─ произвольная отличная от x_>1> точка фазового пространства, а u_>0> ─ произвольная точка области U. Предположим, что объект находится в момент t_>0> в фазовом состоянии x_>0> и движется в течение некоторого времени под воздействием постоянного управления u= u_>0>. Фазовую траекторию объекта при этом движении обозначим через y(t)=(y¹(t),…, yⁿ(t)). Таким образом, фазовая траектория y(t) при t>t_>0> удовлетворяет уравнениям

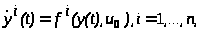(1.9)

(см. (1.2), (1.3)) и начальному условию

y(t_>0>)=x_>0>. (1.10)

Если мы будем двигаться из точки x_>0> до точки y(t) (по рассматриваемой фазовой траектории), то затратим на это движение время t ─ t_>0>. Двигаясь затем из точки y(t) оптимально, мы затратим на движение от точки y(t) до точки x_>1> время T(y(t)). В результате мы совершим переход из точки x_>0> в точку x_>1>, затратив на этот переход время (t ─ t_>0>)+T(y(t)). Но так как оптимальное время движения от точки x_>0> до точки x_>1> равно T(x_>0>), т. е. равно T(y(t_>0>)), то T(y(t_>0>))≤(t ─ t_>0>)+T(y(t)). Заменяя функцию T через ω (см. (1.8)) и разделив обе части неравенства на положительную величину t ─ t_>0>, получаем отсюда и поэтому, переходя к пределу при t→t_>0>, находим

│_>при >_> >≤1. (1.11)

Но производная, указанная в левой части этого неравенства, вычисляется по формуле полной производной Поэтому согласно (1.9) и (1.10) неравенство (1.11) принимает вид Точки x_>0>, u_>0> здесь были произвольными. Таким образом, для любой (отличной от x_>1>) точки x фазового пространства и любой точки u области управления U выполнено соотношение

(1.12)

Пусть теперь (u(t), x(t)) ─ оптимальный процесс, переводящий объект из фазового состояния x_>0> в состояние x_>1>, и t_>0>≤t≤t_>1> ─ отрезок времени, в течение которого это оптимальное движение происходит, так что x(t_>0>)= x_>0>, x(t_>1>)=x_>1> и t_>1>=t_>0 >+ T(x_>0>). Движение по рассматриваемой оптимальной траектории от точки x_>0> до точки x(t) осуществляется в течение времени t ─ t_>0>, а движение от точки x(t) до точки x_>1> ─ в течение времени T(x_>0>) ─ (t ─ t_>0>). Быстрее, чем за время T(x_>0>) ─ (t ─ t_>0>), из точки x(t) попасть в точку x_>1> невозможно. Итак, T(x_>0>) ─ (t ─ t_>0>) есть время оптимального движения из точки x(t) в точку x_>1>, т. е. T(x(t))= T(x_>0>) ─ (t ─ t_>0>). Заменив здесь T через ω, т. е. ω(x(t))= ω(x_>0>) + t ─ t_>0>) и взяв производную по t, получаем

t_>0>≤t≤t_>1>. (1.13)

Таким образом, для каждого оптимального процесса в течение всего движения выполняется равенство (1.13).

Если мы теперь введём в рассмотрение функцию

B(x, u(t))=, (1.14)

То соотношения (1.12) и (1.13) могут быть записаны следующим образом:

B(x, u)≤1 для всех точек x≠x_>1> и u; (1.15)

B(x, u)≡1 для любого оптимального процесса (u(t), x(t)). (1.16)

Итак, справедлива следующая

Т е о р е м а 1.1. Если для управляемого объекта, описываемого уравнением (1.5) и предписанного конечного состояния x_>1> выполнены гипотезы 1 и 2, то имеют место соотношения (1.15) и (1.16) (оптимальность понимается в смысле быстродействия).

Эта теорема и составляет сущность метода динамического программирования для рассматриваемой задачи. Эту теорему можно сформулировать и несколько иначе. Написав соотношение (1.16)

Для t=t_>0>, получим B(x_>0>, u(t_>0>))=1, т. е. для любой точки x_>0> (отличной от x_>1>) найдётся в U такая точка u (а именно u=u(t_>0>)), что B(x_>0>, u)=1. В сопоставлении с неравенством (1.15) получаем соотношение

для любой точки x≠x_>1>. (1.16^*)

Метод динамического программирования (1.15), (1.16) (или, что то же самое, (1.16^*), (1.16)) содержит некоторую информацию об оптимальных процессах и потому может быть использован для их разыскания. Однако он имеет ряд неудобств. Во-первых, применение этого метода требует нахождения не только оптимальных управлений, но и функции ω(x), так как эта функция входит в соотношения (1.15) ─ (1.16^*). Во-вторых, уравнение Беллмана (1.16^*) (или соотношения (1.15), (1.16)) представляет собой уравнение в частных производных относительно функции ω, осложнённое к тому же знаком максимума. Указанные обстоятельства сильно затрудняют возможность пользования методом динамического программирования для отыскания оптимальных процессов в конкретных примерах. Но самым главным недостатком этого метода является предположение о выполнении гипотез 1 и 2. Ведь оптимальные управления и функция ω нам заранее не известны, так что гипотезы 1 и 2 содержат предположение о неизвестной функции, и проверить выполнение этих гипотез по уравнениям движения объекта невозможно. Этот недостаток можно было бы считать не особенно существенным, если бы после решения оптимальной задачи этим методом оказалось, что функция ω(x) действительно является непрерывно дифференцируемой. Но дело заключается в том, что даже в простейших, линейных задачах оптимального управления функция ω(x) не является, как правило, всюду дифференцируемой. Тем не менее, методом динамического программирования можно нередко пользоваться как ценным эвристическим средством.

Принцип максимума. Продолжим теперь рассуждения предыдущего пункта, предположив функцию ω(x) уже дважды непрерывно дифференцируемой (всюду, кроме точки x_>1>). Итак, будем предполагать, что выполнена следующая

Г и п о т е з а 3. функция ω(x) имеет при x≠x_>1> вторые непрерывные производные i, j=1,2,…,n, а функции fⁱ(x, u) ─ первые непрерывные производные где i, j=1,2,…,n.

Пусть (u(t), x(t)), t_>0>≤t≤t_>1>, ─ оптимальный процесс, переводящий объект (1.2) (или (1.3)) из фазового состояния x_>0> в состояние x_>1>. Фиксируем некоторый момент времени t, t_>0>≤t≤t_>1>, и рассмотрим функцию B(x, u(t))= переменного x. В силу гипотезы 3 вытекает, что функция B(x, u(t)) всюду, кроме точки x_>1>, имеет непрерывные производные по переменным x¹,x²,…,xⁿ:

(1.17)

В частности, так как x(t)≠x_>1> (поскольку t<t_>1>), то функция B(x, u(t)) имеет вблизи точки x=x(t) непрерывные производные по переменным x¹,x²,…,xⁿ. Далее, мы имеем в силу (1.15), (1.16) B(x, u(t))≤1 для любого x≠x_>1>; B(x, u(t))=1 при x=x(t).

Эти два соотношения означают, что функция B(x,u(t)) достигает в точке x=x(t) максимума, и потому её частные производные по x¹,…,xⁿ обращаются в нуль в этой точке:

(1.18)

Кроме того, дифференцируя функцию по t, находим

Поэтому соотношение (1.18) может быть переписано в следующем виде:

(1.19)

Заметим теперь, что в формулы (1.15), (1.16), (1.17) и (1.19) сама функция ω не входит, а входят только её частные производные . Поэтому мы введём для удобства следующие обозначения:

(1.20)

Тогда функция B (см. (1.14)) записывается таким образом:

B(x(t), u(t))=

и соотношение (1.16) принимает вид

, для оптимального процесса (x(t), u(t)), t_>0>≤t<t_>1>. (1.21)

Кроме того, согласно (1.15)

для любой точки uU и всех t_>0>≤t<t_>1>. (1.22)

Наконец, соотношения (1.19) записываются следующим образом:

(1.23)

Итак, если (u(t), x(t)), t_>0>≤t<t_>1>, ─ оптимальный процесс, то существуют такие функции ψ_>1>(t), ψ_>2>(t),…, ψ_>n>(t) (они определяются равенствами (1.20)), что имеют место соотношения (1.21), (1.22), (1.23).

Рассмотрение левых частей соотношений (1.21), (1.22) подсказывает нам, что целесообразно ввести в рассмотрение следующую функцию:

(1.24)

зависящую от 2n+r аргументов ψ_>1>, ψ_>2>,…, ψ_>n>, x¹,…, xⁿ, u¹,…, u^r. С помощью этой функции соотношения (1.21), (1.22) записываются в следующем виде:

для оптимального процесса (u(t), x(t)), t_>0>≤t<t_>1>, (1.25)

где ψ(t)=(ψ_>1>(t),…,ψ_>n>(t)) определяются равенствами (1.20);

для любой точки uU и всех t_>0>≤t<t_>1>. (1.26)

Вместо неравенства (1.26) мы можем в силу (1.25) написать следующее соотношение:

t_>0>≤t<t_>1>. (1.27)

Наконец, соотношения (1.23) можно, очевидно, переписать так:

(1.28)

Итак, если (u(t), x(t)), t_>0>≤t<t_>1>, ─ оптимальный процесс, то существует такая функция ψ(t)=(ψ_>1>(t),…, ψ_>n>(t)), что выполняются соотношения (1.25), (1.27), (1.28), где функция H определяется соотношением (1.24).

Так как в соотношениях (1.24), (1.25), (1.27), (1.28) нигде не участвует явно функция ω(x), то равенства (1.20), выражающие функции ψ_>1>(t),…, ψ_>n>(t) через ω, никаких добавочных сведений не дают, и о них можно забыть, ограничившись утверждением, что какие-то функции ψ_>1>(t),…, ψ_>n>(t), удовлетворяющие перечисленным соотношениям (1.25), (1.27), (1.28), существуют. Соотношения (1.28) представляют собой систему уравнений, которым эти функции удовлетворяют. Заметим, что функции ψ_>1>(t),…, ψ_>n>(t) составляют нетривиальное решение этой системы (т. е. ни в какой момент времени t все эти функции одновременно в нуль не обращаются); действительно, если бы при некотором t было ψ_>1>(t)= ψ_>2>(t)=…=ψ_>n>(t)=0, то в силу (1.24) мы получили бы H(ψ(t), x(t), u(t))=0, что противоречит равенству (1.25). Таким образом, мы получаем следующую теорему, которая носит название принципа максимума.

Т е о р е м а 1.2. Предположим, что для рассматриваемого управляемого объекта, описываемого уравнением (в векторной форме)

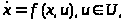(A)

и предписанного конечного состояния x_>1> выполнены гипотезы 1, 2 и 3. Пусть (u(t), x(t)), t_>0>≤t≤t_>1>, ─ некоторый процесс, переводящий объект из начального состояния x_>0 >в состояние x_>1>. Введём в рассмотрение функцию H, зависящую от переменных x¹(t),…, xⁿ(t), u¹,…,u^r и некоторых вспомогательных переменных ψ_>1>(t),…, ψ_>n>(t) (см. (1.24)):

(B)

С помощью этой функции H запишем следующую систему дифференциальных уравнений для вспомогательных переменных:

(C)

где (u(t), x(t)) ─ рассматриваемый процесс (см. (1.28)). Тогда, если процесс (u(t), x(t)), t_>0>≤t<t_>1>, является оптимальным, то существует такое нетривиальное решение ψ(t)=(ψ_>1>(t),…, ψ_>n>(t)), t_>0>≤t<t_>1>, системы (C), что для любого момента t, t_>0>≤t<t_>1>, выполнено условие максимума

(D)

(см. (1.27)) и условие (1.25) H(ψ(t),x(t),u(t))=1.

Однако в приведённой здесь форме принцип максимума страдает одним недостатком: он выведен в предположение дифференцируемости (и даже двукратной) функции ω(x), а эта функция в действительности не является (в обычно встречающихся случаях) всюду дифференцируемой.

Из-за предположения о выполнении сформулированных гипотез (о функции ω(x)) принцип максимума в том виде, в каком он сформулирован выше, не является удобным условием оптимальности. По форме он выведен как необходимое условие оптимальности: если процесс оптимален, то выполнено соотношение (1.16^*) и соответственно (D), т. е. выполнение этого условия необходимо для оптимальности. Однако это условие выведено лишь в предположении выполнения гипотез 1, 2, 3, а их выполнение отнюдь не необходимо для оптимальности. Вот почему сформулированные выше теоремы не могут считаться необходимыми условиями оптимальности.

Замечательным, однако, является тот факт, что если в теореме 1.2 решение ψ(t) и условие максимума (D) рассматривать на всём отрезке t_>0>≤t≤t_>1> (а не только при t_>0>≤t<t_>1>), а заключительное условие

H(ψ(t_>1>), x(t_>1>), u(t_>1>))≥0, (E)

то в этой форме принцип максимума будет справедлив без каких бы то ни было предположений о функции ω, т. е. принцип максимума станет весьма удобным и широко применимым необходимым условием оптимальности.

§ 3. Пример. Задача синтеза

Пример применения принципа максимума. В этом пункте мы разберём один пример вычисления оптимальных процессов. Именно, рассмотрим управляемый объект, упомянутый в п. 3 (см. уравнения (1.1)), при условии, что сила трения и упругая сила отсутствуют (т. е. b=0, k=0), масса m равна единице (m=1), а управляющий параметр подчинён ограничениям |u|≤1. Иначе говоря, мы рассматриваем материальную точку G массы m=1 (см. рис. 10), свободно и без трения движущуюся по горизонтальной прямой и снабжённую двигателем, развивающим силу u, где |u|≤1. Согласно (1.1) уравнения движения этого объекта имеют вид:

(1.29)

─1≤u≤1. (1.30)

Для этого объекта рассмотрим задачу о быстрейшем попадании в начало координат (0, 0) из заданного начального состояния x_>0>=(x_>0>¹, x_>0>²). Иначе говоря, будем рассматривать задачу об оптимальном быстродействии в случае, когда конечным положением служит точка x_>1>=(0, 0). Механически это означает, что материальную точку, имеющую заданное положение x_>0>¹ и заданную начальную скорость x_>0>², мы хотим за кратчайшее время привести в начало отсчёта с нулевой скоростью (т. е. добиться того, чтобы точка пришла в начало отсчёта и остановилась там).

Функция H в рассматриваемом случае имеет вид

H=ψ_>1>x²+ψ_>2>u (1.31)

(см. (1.29) и (B)). Далее, для вспомогательных переменных ψ_>1>, ψ_>2> мы получаем систему уравнений . Из этой системы уравнений находим: ψ_>1>=d_>1>; ψ_>2>= ─d_>1>t+d_>2>, где d1, d_>2> ─ постоянные интегрирования. Далее, в силу соотношения максимума (D) мы находим, учитывая (1.31) и (1.30):

u(t)= +1, если ψ_>2>(t)>0; u(t)= ─1, если ψ_>2>(t)<0.

Иначе говоря, u(t)=sign ψ_>2>(t)=sign (─ d_>1>t + d_>2>). Отсюда следует, что каждое оптимальное управление u(t), t_>0>≤t≤t_>1>, является кусочно-постоянной функцией, принимающей значения и имеющей не более двух интервалов постоянства (ибо линейная функция ─d_>1>t + d_>2> не более одного раза меняет знак на отрезке t_>0>≤t≤t_>1>).

Для отрезка времени, на котором u1, мы имеем (в силу системы (1.29)) , откуда находим

x¹=1/2(x²)²+c. (1.32)

Т
аким образом, кусок фазовой траектории, для которого u1, представляет собой дугу параболы (1.32). Семейство парабол (1.32) показано на рис. 13 (они получаются друг из друга сдвигом в направлении оси x¹). По этим параболам фазовые точки движутся снизу вверх (ибо = u1, т. е. ).

Аналогично для отрезка времени, на котором u ─1, мы имеем, откуда находим

x¹= ─1/2(x²)² + c’. (1.33)

Семейство парабол (1.33) (также получающихся друг из друга сдвигом в направлении оси x¹) показано на рис. 14. По параболам (1.33) фазовые точки движутся сверху вниз (ибо )

К
ак было указано выше, каждое оптимальное управление u(t) является кусочно-постоянной функцией, принимающей значения и имеющей не более двух интервалов постоянства. Если управление u(t) сначала, в течение некоторого времени, равно +1, а затем равно ─1, то фазовая траектория состоит из двух кусков парабол (рис. 15), примыкающих друг к другу, причём второй из этих кусков лежит на той из парабол (1.33), которая проходит через начало координат (ибо искомая траектория должна вести в начало координат). Если же, наоборот, сначала u= ─1, а затем u= +1, то мы получаем фазовую траекторию, изображённую на рис. 16. На рис. 15, 16 надписаны на дугах парабол соответствующие значения управляющего параметра u.

На рис. 17 изображено всё семейство полученных таким образом фазовых траекторий (здесь AO ─ дуга параболы x¹=1/2(x²)², расположенная в нижней полуплоскости; BO ─ дуга параболы x¹= ─1/2(x²)², расположенная в верхней полуплоскости).

Итак, согласно принципу максимума только изображённые на рис. 17 траектории могут быть оптимальными, причём видно, что из каждой точки фазовой плоскости исходит только одна траектория, ведущая в начало координат, которая может быть оптимальной (т. е. задание начальной точки x_>0> однозначно определяет соответствующую траекторию).

Проблема синтеза оптимальных управлений. Посмотрим на разобранный в предыдущих пунктах пример с несколько иной точки зрения. Найденное выше решение оптимальной задачи можно истолковать следующим образом. Обозначим через v(x)= +1 ниже линии AOB и на дуге AO, v(x)= ─1 выше линии AOB и на дуге BO. Тогда (см. 17) на каждой оптимальной траектории значение u(t) управляющего параметра (в произвольный момент времени t) равно v(x(t)), т. е. равно значению функции v в той точке, в которой в момент t находится движущаяся фазовая точка, пробегающая оптимальную траекторию u(t)=v(x(t)). Это означает, что, заменив в системе (1.29) величину u функцией v(x), мы получим систему

(1.34)

решение которой (при произвольном начальном состоянии x_>0>) даёт оптимальную фазовую траекторию, ведущую в начало координат. Иначе говоря, система (1.34) представляет собой систему дифференциальных уравнений (с разрывной правой частью) для нахождения оптимальных траекторий, ведущих в начало координат.

Рассмотренный пример показывает, что решение задачи об оптимальных управлениях естественно ожидать в следующей форме. Будем решать оптимальную задачу в общей постановке:

(см. п. 3), рассматривая всевозможные начальные состояния и каждый раз предписывая в качестве конечного состояния начало координат O фазового пространства. Тогда (насколько можно судить по разобранному выше примеру) существует такая функция v(x), заданная в фазовом пространстве V принимающая значения в области управления U, что уравнение

(1.35)

определяет все оптимальные траектории, ведущие в начало координат. Иначе говоря, оптимальное управление оказывается естественным искать не в форме u=u(t), а в форме u=v(x), т. е. искомое оптимальное управление в каждый момент зависит лишь от того, в какой точке пространства находится в данный момент фазовая точка.

Функцию v(x), дающую уравнение оптимальных траекторий в форме (1.35), называют синтезирующей функцией, а задачу нахождения синтезирующей функции ─ задачей синтеза оптимальных управлений. В разобранном примере синтезирующая функция была кусочно-непрерывной (даже кусочно-постоянной).

Г л а в а II

ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ

§ 4. Линейная задача оптимального управления

Формулировка задачи. Ниже будут подробно изучены управляемые объекты, движение которых описывается линейными дифференциальными уравнениями относительно величин x¹,…,xⁿ, u¹,…,u^r, т. е. уравнениями вида

i=1,2,…,n, (2.1)

где aⁱ_>α> и bⁱ_>β> ─ некоторые постоянные коэффициенты.

Одним из наиболее важных для приложений является случай, когда каждая из величин u¹,u²,…,u^r в уравнениях (2.1) представляет собой отдельный управляющий параметр, область изменения которого не зависит от значений остальных управляющих параметров и задаётся неравенствами

β=1,…,r. (2.2)

Как было указано выше (см. п. 4), эти неравенства определяют r-мерный параллелепипед.

В дальнейшем при рассмотрении объектов вида (2.1) будет предполагаться, что управляющий параметр u=(u¹, u²,…, u^r) может меняться в замкнутой области управления U, представляющей собой выпуклый многогранник (лежащий в пространстве переменных u¹, u²,…, u^r).

Для того чтобы записать уравнения (2.1) в векторной форме, мы введём в рассмотрение матрицы

(2.3)

элементами которых являются коэффициенты aⁱ_>α>, bⁱ_>β>, входящие в уравнения (2.1). Как обычно, результат применения матрицы A к вектору x=(x¹, x²,…, xⁿ) мы будем обозначать символом Ax, т. е. y=Ax есть n-мерный вектор, координаты которого определяются формулами

(2.4)

Аналогично для любого r-мерного вектора u=(u¹, u²,…, u^r) через Bu обозначается вектор, i-я координата которого равна Таким образом, матрица A определяет линейное отображение координатного n-мерного пространства снова в n-мерное пространство, а матрица B определяет отображение r-мерного пространства в n-мерное.

Пользуясь матрицами A и B, мы можем теперь записать уравнения (2.1) в векторной форме:

(2.5)

Пусть u(t)=(u¹, u²,…, u^r) ─ произвольное допустимое (в смысле п. 4) управление, заданное на некотором отрезке t_>0>≤t≤t_>1>, и x_>0>=(x¹_>0>,…, xⁿ_>0>) ─ некоторая точка фазового пространства. Обозначим θ_>1>, θ_>2>,…, θ_>k> все точки, в которых хотя бы одна из функций u¹(t), u²(t),…, u^r(t) терпит разрыв, причём занумеруем эти точки таким образом, что t_>0><θ_>1><θ_>2><…<θ_>k><t_>1>. Подставив функции u¹(t), u²(t),…, u^r(t) в правые части системы (2.1),мы придём к системе уравнений

(2.6)

или в векторной форме,

(2.7)

Систему (2.7) мы рассмотрим сначала для значений t, удовлетворяющих неравенствам t_>0>≤t≤θ_>1>. На этом отрезке изменения аргумента существуют такие функции x¹(t),…, xⁿ(t), определённые и непрерывные на всём отрезке t_>0>≤t≤θ_>1>, которые, рассматриваемые на интервале t_>0><t<θ_>1>, являются решениями системы (2.6) и, кроме того, удовлетворяют начальным условиям x¹(t_>0>)=x¹_>0>, x²(t_>0>)=x²_>0>,…, xⁿ(t_>0>)=xⁿ_>0> (согласно сведениям из дифференциальных уравнений (см. книгу Л.С. Понтрягина «Обыкновенные дифференциальные уравнения», «Наука», М., 1965 (стр. 23, 24 и 168-172))).

Теперь мы можем рассмотреть систему (2.6) на отрезке θ_>1>≤t≤θ_>2>, воспользовавшись точкой γ_>1>=(x¹(θ_>1>),…, xⁿ(θ_>1>), θ_>1>) в качестве начального значения. На отрезке θ_>1>≤t≤θ_>2> снова существует решение с начальным значением γ_>1>. Это решение мы снова обозначим через x(t)=(x¹(t),…, xⁿ(t)). Теперь функция x(t) построена на отрезке t_>0>≤t≤θ_>2> и непрерывна на всём этом отрезке (и, в частности, в «точке сопряжения» θ_>1>;). Воспользовавшись, далее, новым начальным значением γ_>2>=(x¹(θ_>2>),…, xⁿ(θ_>2>), θ_>2>), мы продолжим эту функцию x(t) на отрезок θ_>2>≤t≤θ_>3> и т. д. В конце концов мы определим x(t) на всём отрезке t_>0>≤t≤t_>1>.

Полученная функция x(t)=(x¹(t),…, xⁿ(t)) непрерывна на всём отрезке t_>0>≤t≤t_>1> и является на нём кусочно-дифференцируемой; именно, во всех точках интервала t_>0><t<t_>1>, кроме θ_>1>, θ_>2>,…, θ_>k>, функция x(t) непрерывно дифференцируема (и удовлетворяет системе (2.6)). Построенную функцию мы будем называть решением системы (2.6) (или уравнения (2.7)), соответствующим управлению u(t), при начальном условии x¹(t_>0>)=x¹_>0>, x²(t_>0>)=x²_>0>,…, xⁿ(t_>0>)=xⁿ_>0>. Наконец, мы будем говорить, что допустимое управление u(t), t_>0>≤t≤t_>1>, переводит фазовую точку из состояния x_>0> в состояние x_>1> (в силу закона движения (2.1) или (2.5)), если соответствующее ему решение x(t) системы (2.1), удовлетворяющее начальному условию x(t_>0>)=x_>0>, приходит в момент t_>1> в точку x_>1>, т. е. удовлетворяет также «конечному» условию x(t_>1>)=x_>1>.

Теперь можно уточнить постановку задачи.

Линейной задачей оптимального управления мы будем называть задачу об отыскании оптимальных быстродействий в случае, когда выполнены следующие три условия:

уравнения движения объекта линейны (см. (2.1) или (2.5));

предписанное конечное состояние x_>1> совпадает с началом координат (0, 0,…, 0) n-мерного фазового пространства переменных x¹, x²,…,xⁿ;

область управления U является r-мерным выпуклым многогранником в r-мерном пространстве (u¹, u²,…, u^r), причём начало координат этого пространства принадлежит многограннику U, но не является его вершиной.

Заметим, что начало координат xⁱ=0, i=1,…,n, является положением равновесия системы

(2.8)

получающейся из системы (2.1) отбрасыванием управлений (т. е. получающейся из (2.1) при u¹=u²=…=u^r=0). Таким образом, условие 2) означает, что ищется управление, переводящее объект из заданного начального состояния x_>0> в положение равновесия.

Принцип максимума. В пункте 6 мы сформулировали необходимое условие оптимальности, называемое принципом максимума. Данный пункт посвящён принципу максимума в случае линейной задачи оптимального управления. Вначале укажем те упрощения в формулировке принципа максимума, которые возникают в этом частном случае (т. е. в случае линейной задачи оптимального управления).

Заметим, прежде всего, что функция H (см. формулу (B) на стр. 10) принимает вид

(2.9)

(Здесь в правой части записаны скалярные произведения; например, ψAx есть скалярное произведение векторов ψ и Ax.)

Далее, рассмотрим систему дифференциальных уравнений для вспомогательных переменных ψ_>1>, ψ_>2>,…, ψ_>n> (см. формулу (C) на стр. 10). Мы имеем

Следовательно, система уравнений для вспомогательных переменных принимает вид

(2.10)

т. е. представляет собой так называемую сопряжённую систему (по отношению к линейной системе (2.8)). В векторной форме система (2.10) записывается в виде

(2.11)

где

─ матрица, получающаяся из матрицы A транспонированием (т. е. заменой строк столбцами).

Так как в правой части соотношения (2.9) первое слагаемое совсем не зависит от u, то при написании соотношения (D) (см. стр. 11) достаточно рассмотреть лишь второе слагаемое. Таким образом, соотношение (D) принимает в рассматриваемом случае вид

(2.12)

для любого момента τ, t_>0>≤τ≤t_>1>.

Наконец, соотношение (E) (стр. 11) становится просто ненужным, так как в рассматриваемом случае оно всегда выполняется. Действительно, так как x(t_>1>)=(0, 0,…, 0) (условие 2) на стр. 15), то в H(ψ(t_>1>), x(t_>1>), u(t_>1>)) первое слагаемое обращается в нуль (см. (2.9)). Второе же слагаемое, в силу (2.12), заведомо неотрицательно, ибо при u¹=…=u^r=0 (эта точка, в силу условия 3) на стр.15, принадлежит многограннику U) мы имеем ψ(τ)Bu=0, а потому максимальное значение выражения ψ(τ)Bu неотрицатнльно. Итак, соотношение H(ψ(t_>1>), x(t_>1>), u(t_>1>))0 для линейной оптимальной задачи всегда выполнено.

Сказанное можно резюмировать следующим образом. Пусть u(t), t_>0>tt_>1>,  допустимое управление, переводящее объект (2.5) из заданного начального состояния x_>0> в положение равновесия (0, 0,…, 0). Будем говорить, что управление u(t) удовлетворяет принципу максимума, если существует такое нетривиальное решение (t) уравнения (2.11), для которого выполняется условие максимума (2.12) (в каждый момент времени , t_>0>t_>1>). Для оптимальности управления u(t) необходимо, чтобы оно удовлетворяло принципу максимума. Это и есть та упрощённая формулировка принципа максимума, к которой мы приходим в случае линейной задачи оптимального управления.

Принцип максимума — необходимое и достаточное условие оптимальности. Замечательным фактом является то, что в случае линейной задачи оптимального управления принцип максимума представляет собой не только необходимое, но и достаточное условие оптимальности. Однако факт этот имеет место не для произвольной линейной задачи — имеются малосущественные исключения. Поэтому мы наложим на линейную задачу некоторое ограничение, называемое условием общности положения. Сформулируем это условие:

Условие общности положения: если  — вектор, параллельный произвольному ребру многогранника U, то вектор B не принадлежит никакому собственному инвариантному подпространству относительно преобразования A. Невыполнение условия общности положения означает, что хотя бы для одного ребра многогранника U векторы B, AB, A²B,…, A^n-1B линейно зависимы, т. е. определитель n-го порядка, составленный из координат этих векторов, обращается в нуль. Однако всюду в дальнейшем условие общности положения предполагается (если не оговорено противное) выполненным.

Теперь перейдём к теореме, упоминавшейся в начале этого пункта.

Т е о р е м а 2.1. Пусть u(t), t_>0>tt_>1>, — допустимое управление, переводящее объект из заданного начального состояния x_>0> в положение равновесия (0, 0,…, 0). Для оптимальности управления u(t) необходимо и достаточно, чтобы оно удовлетворяло принципу максимума.

Основные теоремы о линейных оптимальных быстродействиях.

Т е о р е м а 2.2. Для каждого нетривиального решения (t) уравнения (2.11) соотношение (2.12) однозначно определяет допустимое управление u(t); при этом оказывается, что функция u(t) кусочно-постоянна и её значениями являются лишь вершины многогранника U.

Каждую точку разрыва оптимального управления мы будем называть точкой переключения.

Т е о р е м а 2.3. Предположим, что многогранник U является r-мерным параллелепипедом (2.2) и что все собственные значения матрицы A=(aⁱ_>j>), составленной из коэффициентов уравнений (2.1), действительны. Тогда в оптимальном управлении u(t)=(u¹(t),…, u^r(t)) каждая из функций u^(t), =1,…,r, кусочно-постоянна, принимает только значения a^ и b^ (см. (2.2)) и имеет не более n-1 переключений (т. е. не более n интервалов постоянства), где n — порядок системы (2.1).

Т е о р е м а 2.4 (т е о р е м а е д и н с т в е н н о с т и). Пусть u_>1>(t) и u_>2>(t) — два оптимальных управления, заданных соответственно на отрезках t_>0>tt_>1> и t_>0>tt_>2> и переводящих точку x_>0> в начало координат. Тогда эти управления совпадают, т. е. t_>1>=t_>2> и u_>1>(t)u_>2>(t) на отрезке t_>0>tt_>1>.

Областью управляемости для объекта (2.5) мы будем называть множество всех точек x_>0> фазового пространства X, из которых возможно при помощи какого-либо допустимого управления попасть в начало координат. Само начало координат мы также будем причислять к области управляемости. Ясно, что вопрос о нахождении оптимальных процессов разумно ставить лишь в случае, если начальное фазовое состояние x_>0> принадлежит области управляемости (ведь из точек, не принадлежащих области управляемости, вообще нельзя попасть в начало координат).

Т е о р е м а 2.5 (т е о р е м а с у щ е с т в о в а н и я). Область управляемости является выпуклым открытым множеством фазового пространства X; для любой точки x_>0>, принадлежащей области управляемости, существует оптимальное управление, переводящее точку x_>0> в начало координат.

Т е о р е м а 2.6. Если в линейной задаче оптимального управления матрица A (см. (2.3)) устойчива, т. е. все её собственные значения имеют отрицательные действительные части, то область управляемости совпадает со всем фазовым пространством X. Следовательно, для любой точки x_>0>X существует оптимальное управление, переводящее фазовую точку x_>0> в начало координат.

§ 5. Решение задачи синтеза для линейных задач второго порядка

Упрощение уравнений линейного управляемого объекта. Нередко бывает, что в линейной задаче общая запись уравнений движения объекта в виде (2.1) неудобна и целесообразно воспользоваться некоторыми упрощениями. Мы здесь отметим стандартные упрощения, которые можно осуществить с помощью замены координат.

Прежде всего, рассмотрим вопрос о замене координат в фазовом пространстве X рассматриваемого управляемого объекта. Предположим, что в пространстве X вместо координат x¹,…, xⁿ введены новые координаты y¹,…, yⁿ, связанные с прежними координатами соотношениями

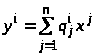(2.13)

(где матрицы P=(pⁱ_>j>) и Q=(qⁱ_>j>) взаимно обратны). Ясно, что при такой замене линейная система (2.1) превращается в новую линейную систему

коэффициенты которой легко вычисляются:

Таким образом, ,

Переходя к векторным обозначениям, можно сказать, что указанная замена координат переводит уравнение (2.5) в уравнение где матрицы C и D выражаются через матрицы A, B, P, Q по формулам C=QAP, D=QB.

Очевидно, при такой замене условия 1), 2), указанные на стр. 15, сохраняются и для уравнения получаемого после замены. Далее, каждый процесс (u(t), x(t)), удовлетворяющий уравнению переходит в процесс (u(t), y(t)), удовлетворяющий уравнению (и обратно). Так как при этом время t не меняется, то указанная замена переводит оптимальные процессы для уравнения (и наоборот). В частности, синтез оптимальных управлений для уравнения переводится с помощью преобразования координат (2.13) в синтез оптимальных управлений для уравнения .

Таким образом, если уравнение окажется проще и для него синтез оптимальных управлений можно будет построить, то из этого синтеза можно (с помощью афинного преобразования (2.13)) получит синтез и для первоначального уравнения . В этом и заключается смысл замены координат (2.13): она позволяет заменить матрицу A трансформированной матрицей C=QAP, в то же время вызывая лишь афинное искажение картины синтеза оптимальных управлений. Таким образом, преобразованием (2.13) можно воспользоваться для упрощения матрицы A, составленной из коэффициентов при фазовых координатах.

Предположим, что в уравнении матрица A уже приведена к простейшему виду (с помощью описанного выше приёма). Укажем теперь, каким образом может быть упрощена матрица B, составленная из коэффициентов при управляющих параметрах.

С этой целью положим

(2.14)

Это означает, что вместо r управляющих параметров u¹,…,u^r вводятся n других управляющих параметров v¹,…, vⁿ, благодаря чему система (2.1) заменяется следующей:

или в векторной форме,

Нужно только выяснить, в каких пределах может изменяться точка v=(v¹, v²,…, vⁿ). Удобно считать, что эта точка v=(v¹, v²,…, vⁿ) расположена в том же пространстве X, что и точка x=(x¹,…, xⁿ).

Соотношения (2.14) определяют линейное отображение r-мерного пространства переменных u¹,…,u^r в фазовое пространство X. Образом многогранника U при отображении (2.14) является некоторый выпуклый многогранник в пространстве X, который мы обозначим через V.

Таким образом, получаем два линейных уравнения:

(2.15)

(2.16)

Г л а в а III

СИНТЕЗ ОПТИМАЛЬНЫХ УПРАВЛЕНИЙ ДЛЯ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА

§ 6. Решение задачи синтеза в случае комплексных собственных значений

Задача синтеза для малых колебаний маятника. Здесь будет дано полное решение задачи синтеза оптимальных управлений для линейных объектов, описываемых уравнениями второго порядка. Фазовое пространство X в этом случае представляет собой плоскость.

Рассмотрим колебание плоского маятника. Как известно колебание маятника, подвешенного к точке опоры, описывается дифференциальным уравнением второго порядка:

(в нашем случае положим β=1)

при малых колебаниях маятника Sinφ≈φ тогда уравнение движения маятника запишется в виде:

(3.1)

Управляющий параметр u (скалярный) будем предполагать изменяющимся в пределах 1u1.

Пусть — угол отклонения, а — скорость маятника. Тогда уравнение (3.1) перепишется в виде следующей нормальной системы:

(3.2)

На плоскости x¹, x² «многогранник» U будет представляться отрезком [1, 1], расположенным на оси x². Легко видеть, что ось x² не является собственным инвариантным подпространством матрицы A, которая для системы (3.2) имеет вид:

A=,

и потому условие общности положения всегда выполнено.

Найдём собственные значения матрицы A. Для этого составим характеристическое уравнение |λE─A|=0, т. е. λ²+λ+1=0. Откуда находим, что собственные значения матрицы A такие:

т. е. собственные значения матрицы A комплексные. Введём обозначения где b≠0.

Тогда матрица A преобразуется к виду:

=.

Будем рассматривать систему, соответствующую матрице , т. е. систему вида:

(3.3)

Вначале рассмотрим соответствующую однородную систему:

(3.4)

Общее решение этой системы имеет вид:

где c, γ – произвольные постоянные интегрирования.

Запишем функцию H и применим принцип максимума.

где ψ_>1>, ψ_>2> определяются системой, сопряжённой к системе (3.3), т. е. системой вида:

(3.5)

Общее решение этой системы имеет вид:

где c’, γ’ – произвольные постоянные интегрирования. Т. е. функция H имеет вид:

Подставим в функцию H представление решений x¹, x²:

Т. к. собственный вектор матрицы A, соответствующий собственному значению  имеет вид q_>1>─iq_>2>, где q_>1>=(1;─1/2); q_>2>=(0;─).

Пусть q_>1> и q_>2> – базисные векторы новой косоугольной системы координат y¹, y². Тогда переход от системы y¹, y² к системе x¹, x² выражается формулами:

Тогда в новых координатах система уравнений (3.2) запишется в виде

или, иначе, в виде

где v=(v¹, v²) ─ управляющая точка, которая может меняться в пределах многогранника V, представляющего собой отрезок [] оси y².

Согласно теории вершинам e_>1>=(0, ), e_>2>=(0, ) многогранника V соответствуют точки h_>1>=(1, ), h_>2>=(-1, ) (координаты указаны в системе y¹, y²), а каждый из углов _>1>, _>2>, соответствующих этим вершинам, равен .

Теперь уже нетрудно построить синтез оптимальных управлений в плоскости y¹, y². Кусками фазовых траекторий будут дуги логарифмических спиралей, т. к. у нас =1, т. е. >0 (рис. 18).

При переходе от координат y¹, y² к координатам x¹, x² картина синтеза афинно искажается.

Список используемой литературы:

1. В.Г. Болтянский. «Математические методы оптимального управле­ния», М.: «Наука», 1968г.

2. Л.С. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, Е.Ф. Мищенко. «Математическая теория оптимальных процессов», 4-е издательство. М.: «Наука», 1983г.

3. Р. Габасов, Ф.М. Кириллова. «Методы оптимизации», Минск, издательство БГУ, 1981г.