Сборник Лекций по матану (работа 1)
Глава 2. Дифференциальное и интегральное исчисление функции одной переменной
§1. Основные понятия
Пусть D — некоторое множество чисел. Если задан закон, по которому каждому числу x из множества D ставится в соответствие единственное определенное число y, то будем говорить, что на множестве D задана функция, которую назовём f. Число y — это значение функции f в точке x, что обозначается формулой y = f(x).
Число x называется аргументом функции, множество D — областью определения функции, а все значения y образуют множество E, которое называется множеством значений или областью изменения функции.
Функция f называется возрастающей (убывающей) на множестве G, если для любых чисел х>1> и х>2> из множества G, таких что x>1> < x>2>, выполняется условие f(x>1>) < f(x>2>) (f(x>1>) > f(x>2>)).
Так как между множеством действительных чисел и множеством точек числовой оси можно установить взаимно-однозначное соответствие, в дальнейшем изложении понятиям “число х” и “точка х числовой оси” в некоторых случаях будет придаваться один и тот же смысл. Например, вместо “значение функции при значении аргумента, равном х>1>” будет говориться “значение функции в точке х>1>”. В нижеследующем определении можно везде заменить выражение “точка х” на выражение “число х”.
Пусть
— некоторое положительное число.
-окрестностью
точки x>0
>называется
множество всех точек x,
принадлежащих промежутку (x>0> , x>0> + ),
кроме самой точки x>0>.
Принадлежность точки x
окрестности
точки
 можно выразить с помощью двойного
неравенства
можно выразить с помощью двойного
неравенства
0 < x – x>0> < .
Число называется радиусом окрестности.
§2. Предел и непрерывность функции
Рассмотрим функцию y = x2 в точке x>0> = 2. Значение функции в этой точке равно 4.
Отметим одну особенность поведения функции в этой точке. Можно

Рассмотрим
функцию
 .
Эта
функция не определена в точке x>0> = 2.
При x>0> 2
её можно преобразовать:
.
Эта
функция не определена в точке x>0> = 2.
При x>0> 2
её можно преобразовать:
 .
.

Введем понятие предела функции. Число A называется пределом функции y = f(x) в точке x>0> (иногда говорят, при x, стремящемся к x>0>), если для любого положительного числа можно найти такое положительное число , что для всех x из -окрестности точки x>0> соответствующие значения y попадают в -окрестность точки y = A.
Можно сформулировать определение предела функции по-другому. Число A называется пределом функции y = f(x) в точке x>0>, если для любого положительного числа можно найти такое положительное число , что для всех x, удовлетворяющих условию
0 < x – x>0> < ,
выполняется условие
y – A < .
Тот факт, что A есть предел функции y = f(x) в точке x = x>0>, записывается формулой

 .
.
Как видно из второго из рассмотренных выше примеров, для того, чтобы функция имела предел в точке x = x>0>, не требуется, чтобы она была определена в этой точке.
Рассмотрим
функцию
 .
Очевидно, что если x > 0,
то y = 2x;
если x < 0,
то y = –2x;
при x = 0
функция не определена.
.
Очевидно, что если x > 0,
то y = 2x;
если x < 0,
то y = –2x;
при x = 0
функция не определена.
График функции изображен на рисунке 3. Легко убедиться в том, что, согласно приведенному выше определению предела, эта функция в точке x = 0 предела не имеет.
Функция
y = f(x)
называется непрерывной
в точке
x = x>0>,
если она определена в этой точке и ее
значение f(x>0>)
равно пределу функции в этой точке:
 .
.
Функция
y = x2
непрерывна
в точке
x = 2,
как и во всех точках числовой оси. Функция
 не является непрерывной в точке x = 2.
Функция
не является непрерывной в точке x = 2.
Функция
 не является непрерывной в точке x = 0.
не является непрерывной в точке x = 0.
 Функция,
непрерывная в каждой точке открытого
промежутка, называется непрерывной
на этом промежутке.
Функция,
непрерывная в каждой точке открытого
промежутка, называется непрерывной
на этом промежутке.
Приведем свойства предела функции.
1. Функция не может иметь в одной точке два разных предела.
2.
 ,
если C —
постоянная функция.
,
если C —
постоянная функция.
3.
Если существует и
C
— постоянная функция, то
и
C
— постоянная функция, то
 .
.
4. Если
существуют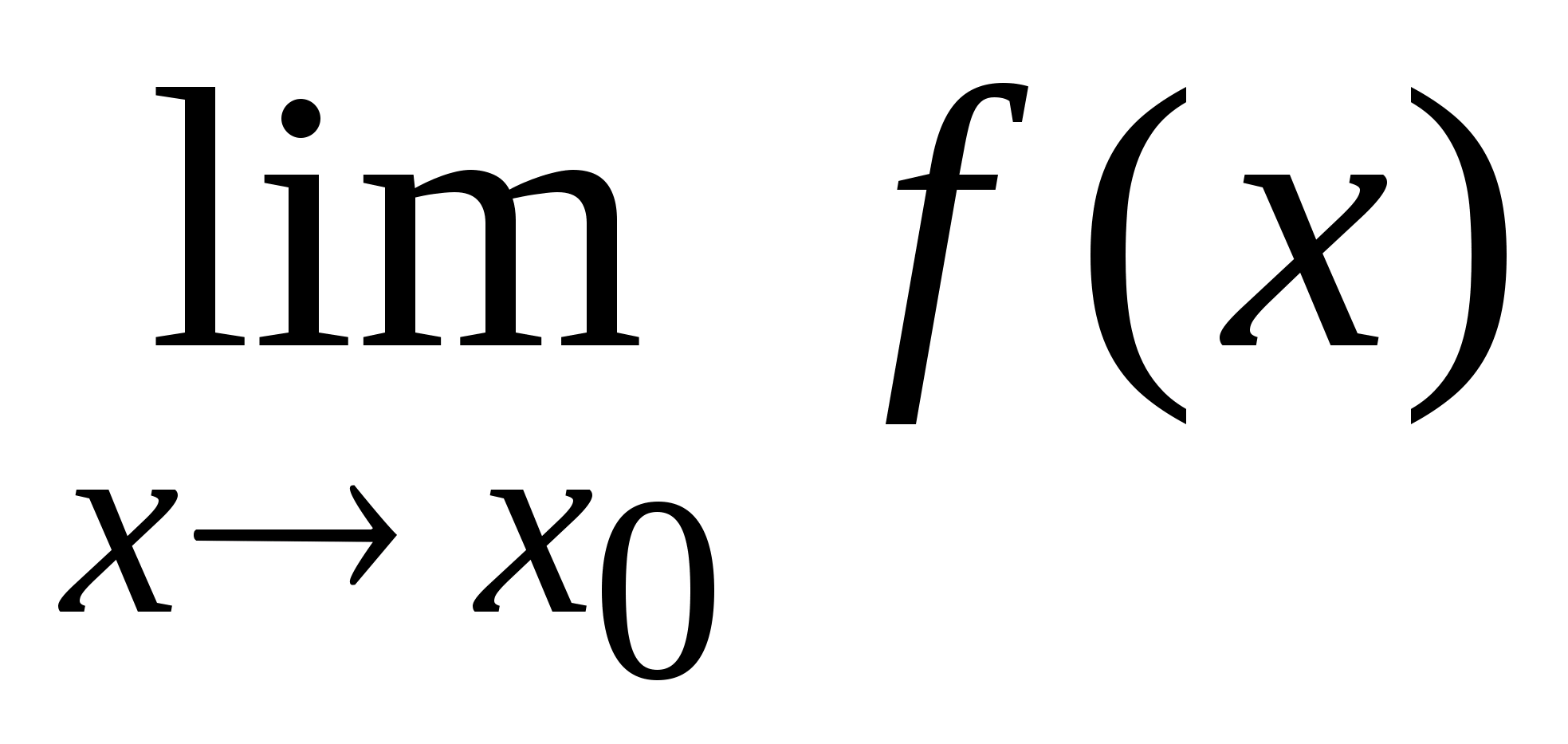 и
и
 ,
то существует
,
то существует
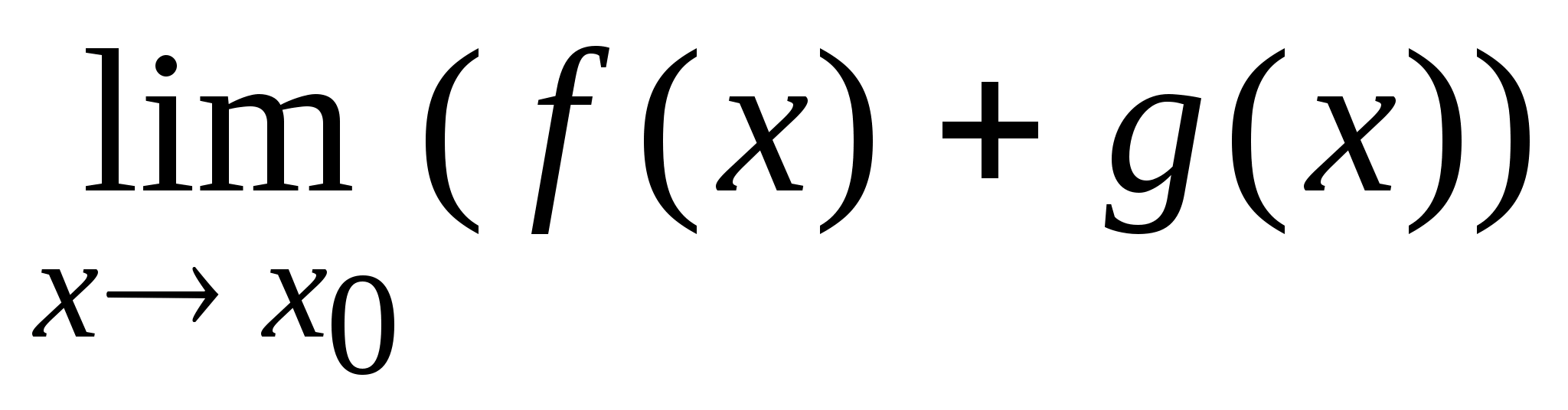 ,
равный
,
равный
 ,
а
также существует
,
а
также существует
 ,
равный
,
равный
 .
Если
при этом
.
Если
при этом
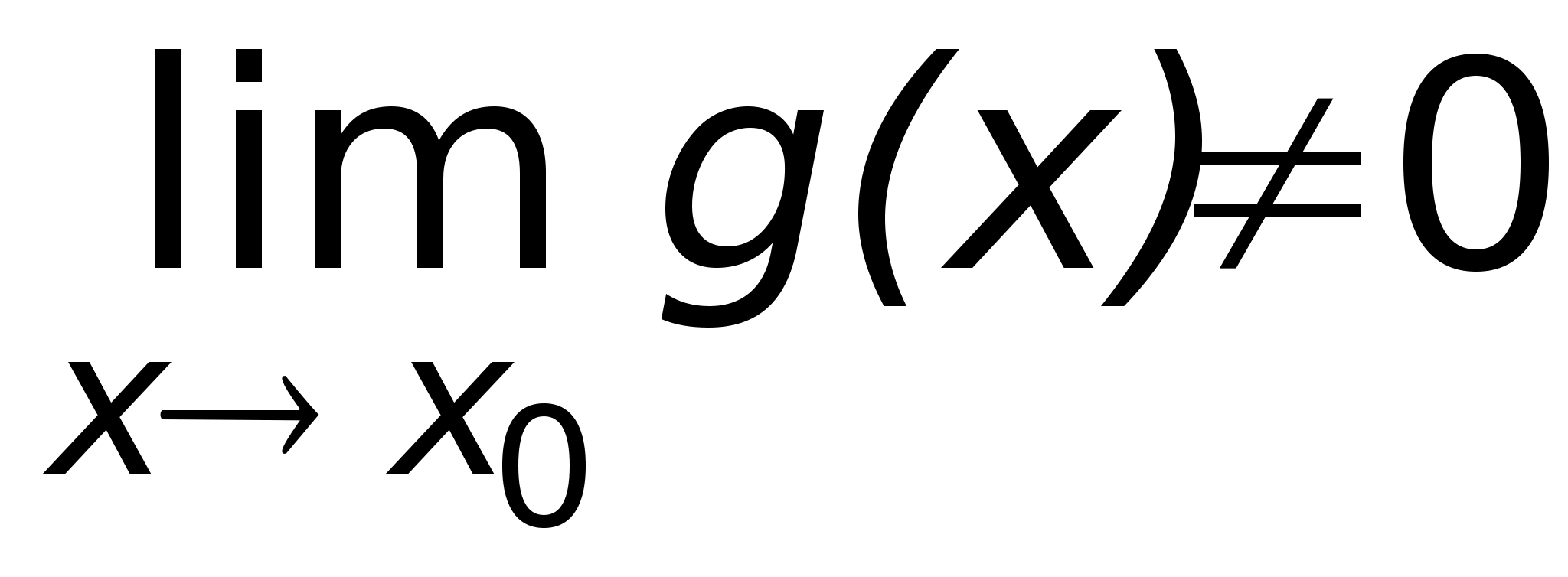 ,
то существует
,
то существует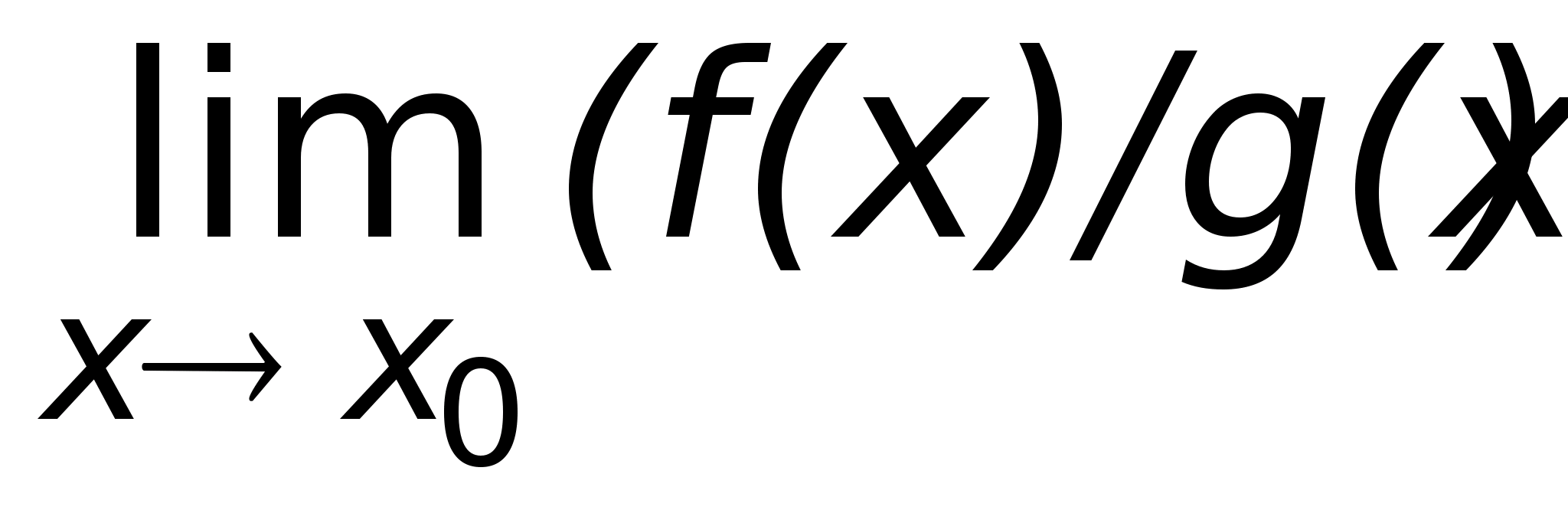 ,
равный
,
равный
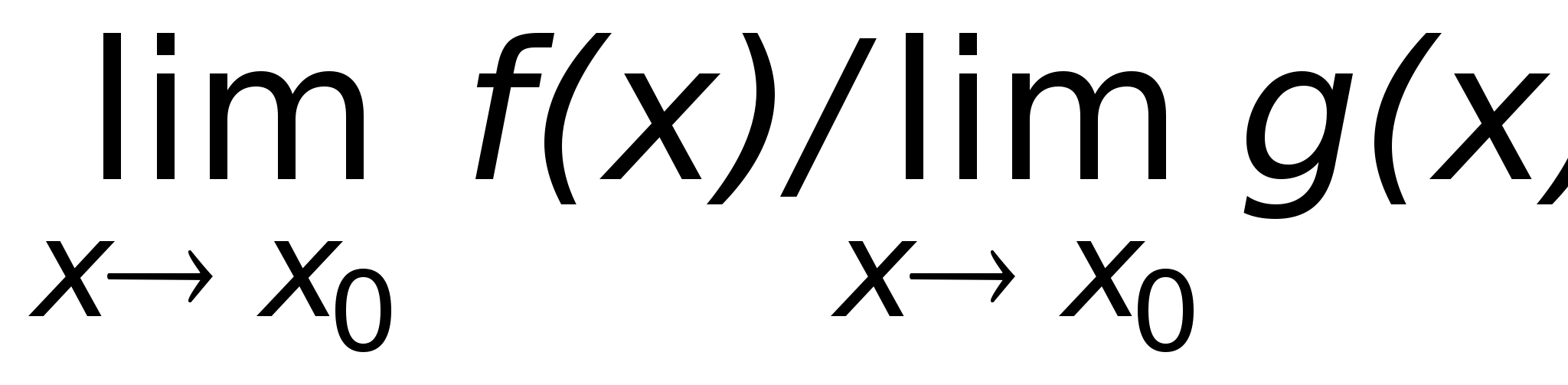 .
.
Введем определения так называемых “односторонних пределов”.
Число
B
называется пределом
функции f(x)
в точке a
справа
(это записывается в виде формулы
 ),
если для любого положительного числа
найдется положительное число ,
такое что из из условия 0 < x – a <
будет следовать B –f(x) < .
),
если для любого положительного числа
найдется положительное число ,
такое что из из условия 0 < x – a <
будет следовать B –f(x) < .
Согласно
приведенному определению
 .
Отметим, что обыкновенного предела
функция
.
Отметим, что обыкновенного предела
функция
 в точке x = 0
не имеет.
в точке x = 0
не имеет.
Число
С
называется пределом
функции f(x)
в точке b
слева
(это записывается в виде формулы
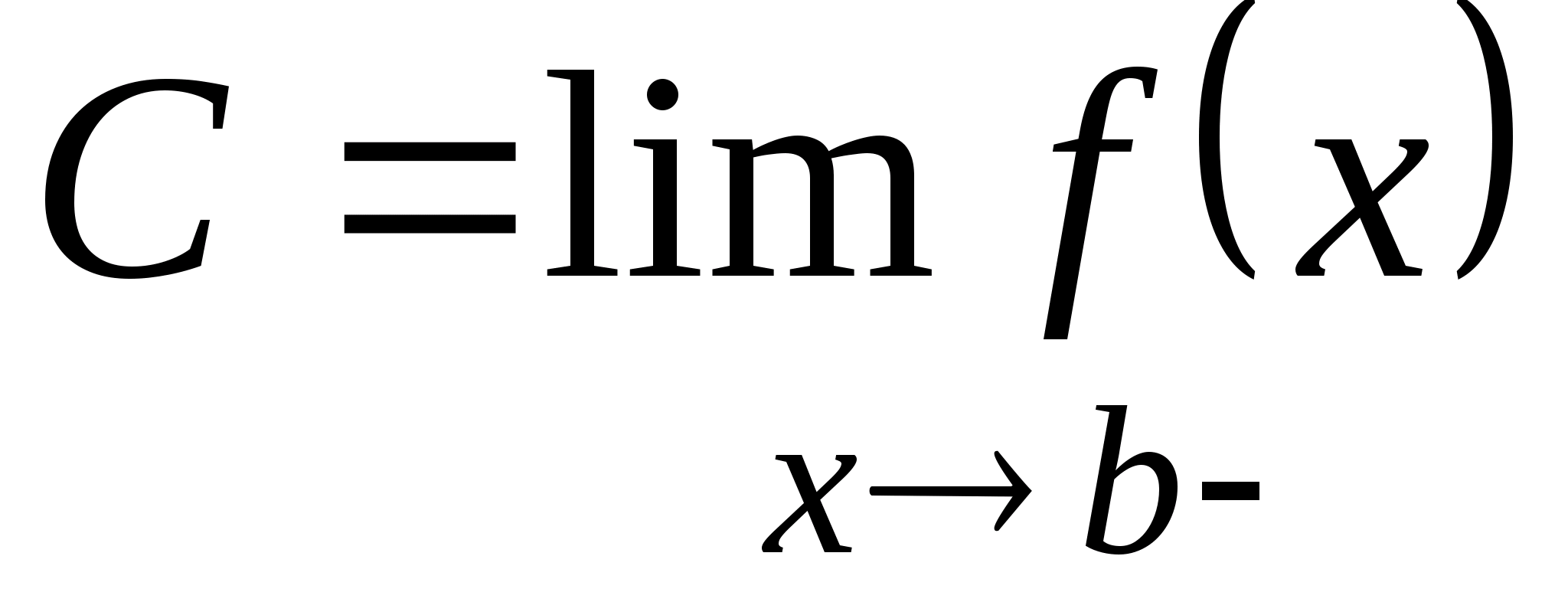 ),
если для любого положительного числа
найдется положительное число
такое, что из условия 0 < b – x <
будет следовать C – f(x) < .
),
если для любого положительного числа
найдется положительное число
такое, что из условия 0 < b – x <
будет следовать C – f(x) < .
Очевидно,
что функция
 (её график, изображен на рисунке 3) имеет
два односторонних предела в точке x = 0:
(её график, изображен на рисунке 3) имеет
два односторонних предела в точке x = 0:
 ;
;
 .
.
Функция f(x) называется непрерывной в точке a справа (непрерывной в точке b слева), если
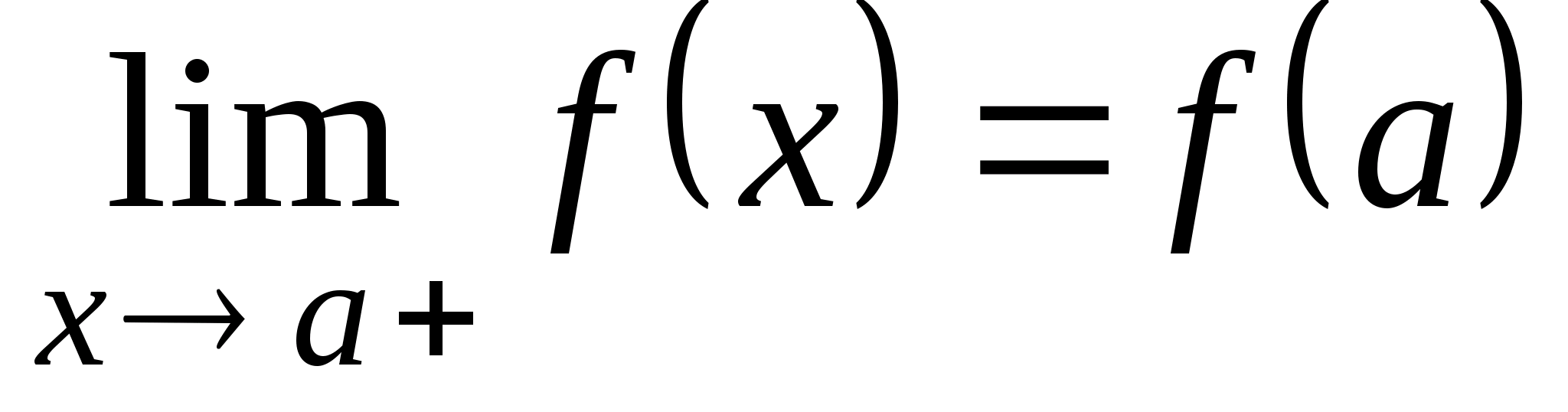 (
(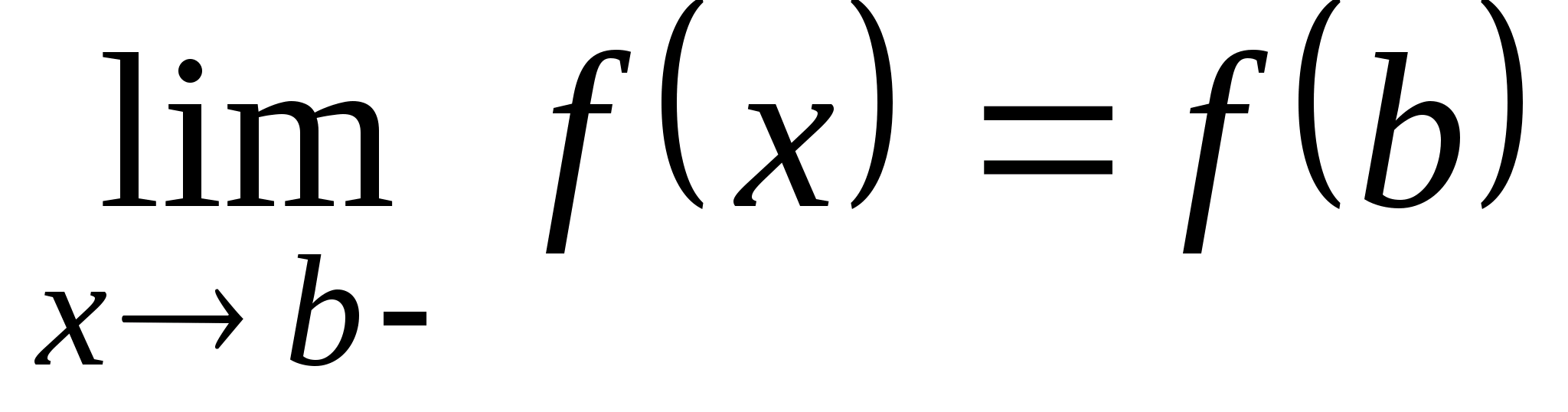 ).
).
Функция
 непрерывна справа в точке x=0.
непрерывна справа в точке x=0.
Функция называется непрерывной на замкнутом промежутке [a, b], если она непрерывна на открытом промежутке (a, b), непрерывна справа в точке a и непрерывна слева в точке b.
Достаточно просто можно доказать теорему, связывающую понятия предела функции в точке и односторонних пределов. Мы ограничимся только формулировкой теоремы.
Для
того, чтобы выполнялось равенство
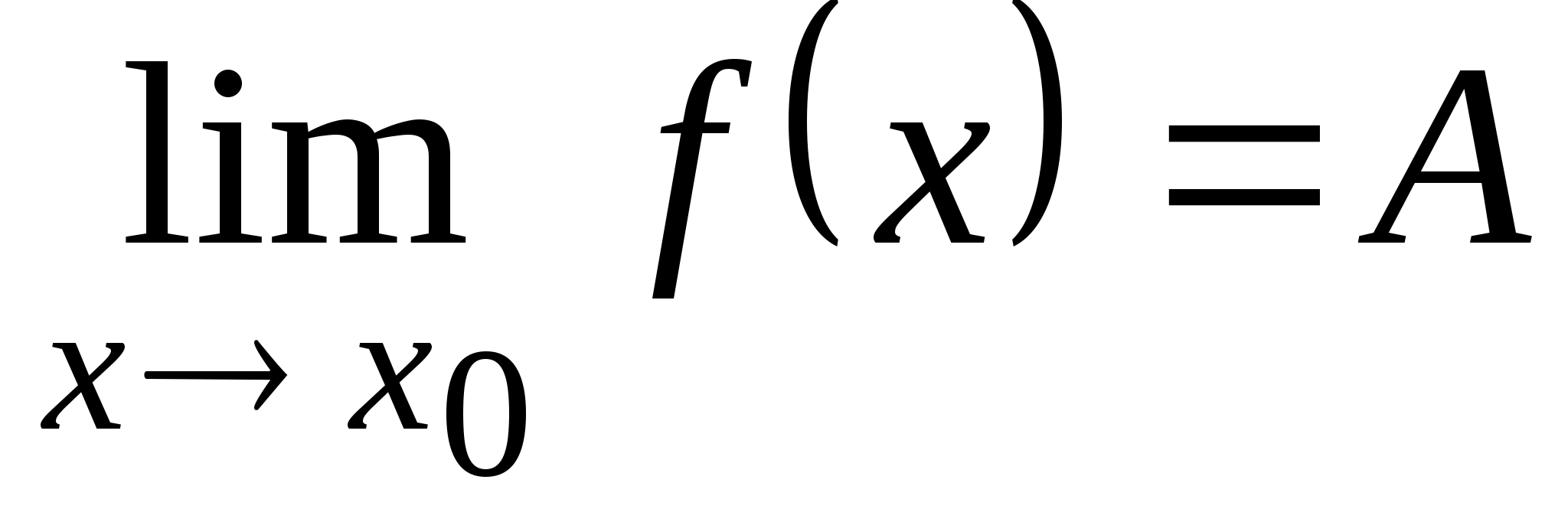 ,
необходимо
и достаточно, чтобы одновременно
выполнялись два равенства:
,
необходимо
и достаточно, чтобы одновременно
выполнялись два равенства:
 ;
;

В дальнейшем нам понадобятся понятия предела функции в бесконечно удалённых точках. Рассмотрим сначала функцию f(x), определенную на полубесконечном промежутке (х>0>; ). Число А называется пределом функции f(x) при х, стремящемся к бесконечности:
 ,
,
если для любого положительного числа можно найти такое положительное число M (зависящее от ), что для всех чисел х, превосходящих М, выполняется условие:
f(x) – A < .
Пусть
теперь функция f(x)
определена на полубесконечном промежутке
(–;
х>0>).
Число
А
называется
пределом функции
f(x)
при
х,
стремящемся
к минус бесконечности:
 ,
,
если для любого положительного числа можно найти такое положительное число M (зависящее от ), что для всех чисел х, меньших, чем – М, выполняется условие:
f(x) – A < .
Отметим два, так называемых, "замечательных предела".
1. 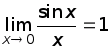 .
Геометрический смысл этой формулы
заключается в том, что прямая
.
Геометрический смысл этой формулы
заключается в том, что прямая
 является касательной к графику функции
является касательной к графику функции
 в точке
в точке
 .
.
2. 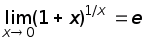 .
Здесь e
— иррациональное число, приблизительно
равное 2,72.
.
Здесь e
— иррациональное число, приблизительно
равное 2,72.
Приведем пример применения понятия предела функции в экономических расчетах. Рассмотрим обыкновенную финансовую сделку: предоставление в долг суммы S>0> с условием, что через период времени T будет возвращена сумма S>T>. Определим величину r относительного роста формулой
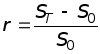 . (1)
. (1)
Относительный рост можно выразить в процентах, умножив полученное значение r на 100.
Из формулы (1) легко определить величину S>T>:
S>T> = S>0>(1 + r)
При расчете по долгосрочным кредитам, охватывающим несколько полных лет, используют схему сложных процентов. Она состоит в том, что если за 1-й год сумма S>0> возрастает в (1 + r) раз, то за второй год в (1 + r) раз возрастает сумма S>1> = S>0>(1 + r), то есть S>2> = S>0>(1 + r)2. Аналогично получается S>3> = S>0>(1 + r)3. Из приведенных примеров можно вывести общую формулу для вычисления роста суммы за n лет при расчете по схеме сложных процентов:
S>n> = S>0>(1 + r)n.
В
финансовых расчетах применяются схемы,
где начисление сложных процентов
производится несколько раз в году. При
этом оговариваются годовая
ставка
r
и количество
начислений за год
k.
Как правило, начисления производятся
через равные промежутки времени, то
есть длина каждого промежутка T>k>
составляет
 часть года. Тогда для срока в T
лет (здесь T
не обязательно является целым числом)
сумма S>T>
рассчитывается по формуле
часть года. Тогда для срока в T
лет (здесь T
не обязательно является целым числом)
сумма S>T>
рассчитывается по формуле
 (2)
(2)
Здесь
 — целая часть числа
— целая часть числа
 ,
которая совпадает с самим числом, если,
например, T
целое число.
,
которая совпадает с самим числом, если,
например, T
целое число.
Пусть годовая ставка равна r и производится n начислений в год через равные промежутки времени. Тогда за год сумма S>0> наращивается до величины, определяемой формулой
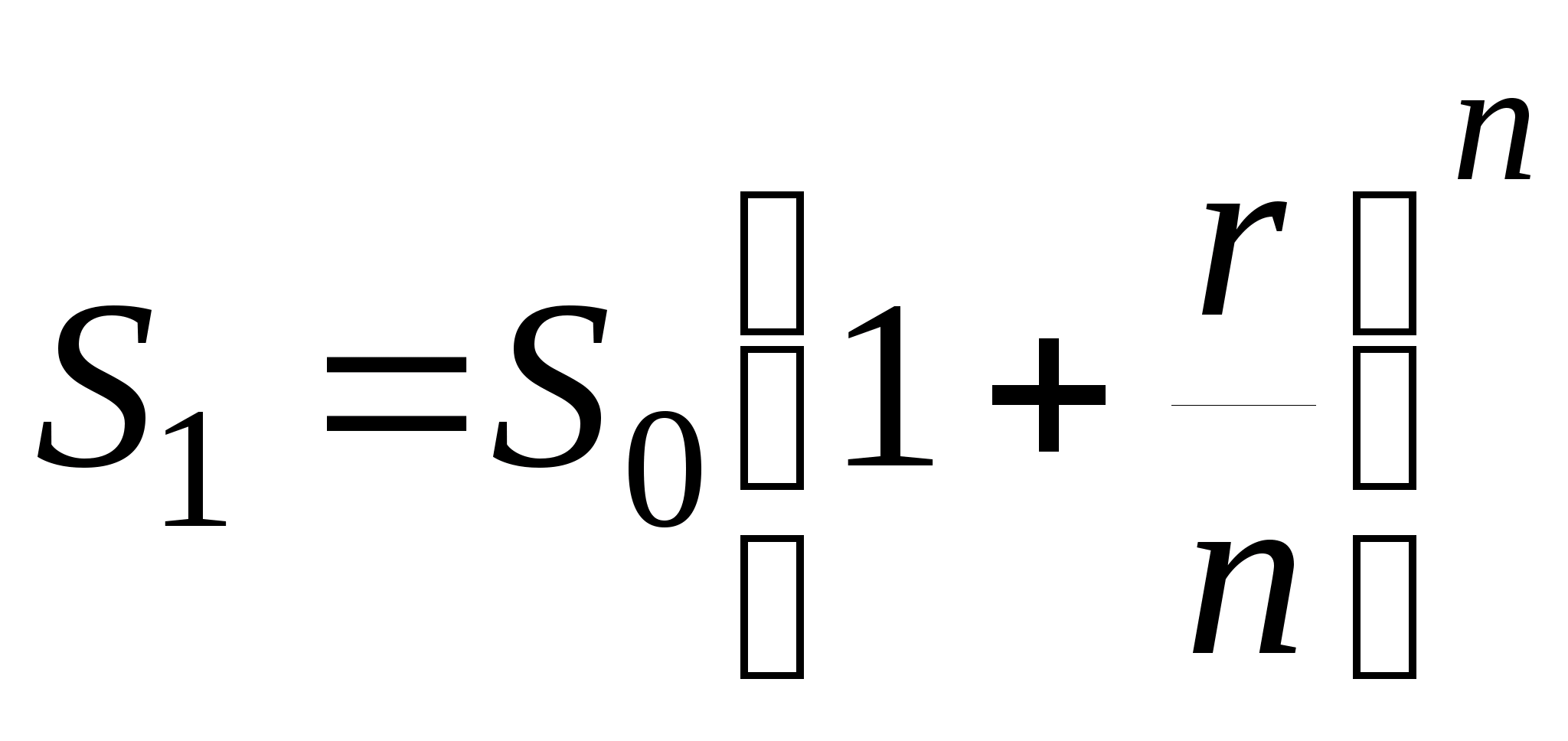 (3)
(3)
В теоретическом анализе и в практике финансовой деятельности часто встречается понятие “непрерывно начисляемый процент”. Чтобы перейти к непрерывно начисляемому проценту, нужно в формулах (2) и (3) неограниченно увеличивать соответственно, числа k и n (то есть устремить k и n к бесконечности) и вычислить, к какому пределу будут стремиться функции S>T> и S>1>. Применим эту процедуру к формуле (3):
 .
.
Заметим, что предел в фигурных скобках совпадает со вторым замечательным пределом. Отсюда следует, что при годовой ставке r при непрерывно начисляемом проценте сумма S>0> за 1 год наращивается до величины S>1>*, которая определяется из формулы
S>1>* = S>0>er. (4)
Пусть теперь сумма S>0> предоставляется в долг с начислением процента n раз в год через равные промежутки времени. Обозначим r>e> годовую ставку, при которой в конце года сумма S>0> наращивается до величины S>1>* из формулы (4). В этом случае будем говорить, что r>e> — это годовая ставка при начислении процента n раз в год, эквивалентная годовому проценту r при непрерывном начислении. Из формулы (3) получаем
 .
.
Приравнивая правые части последней формулы и формулы (4), полагая в последней T = 1, можно вывести соотношения между величинами r и r>e>:
 ,
,
 .
.
Эти формулы широко используются в финансовых расчётах.
§3. Производная
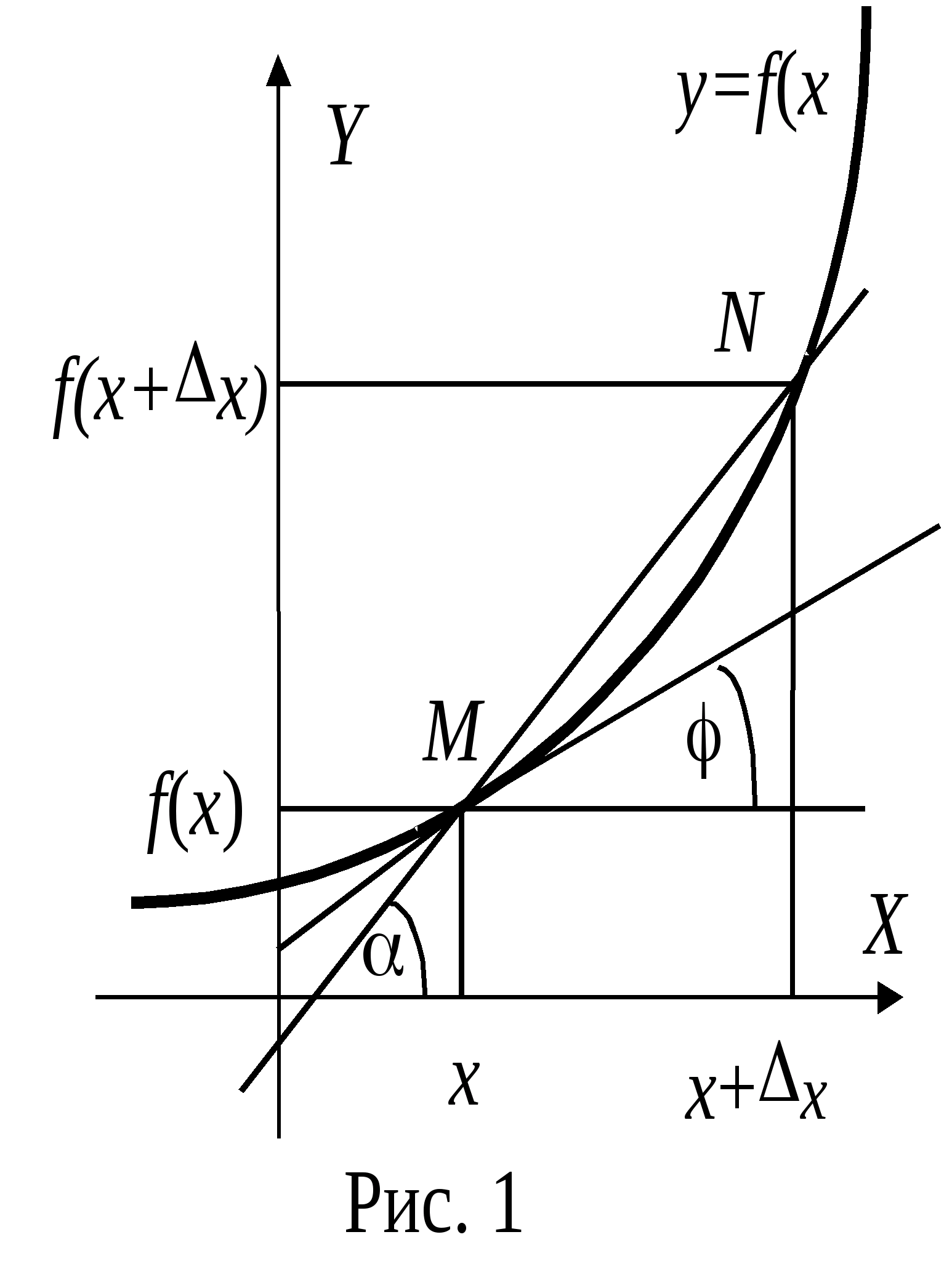
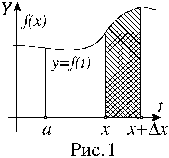
Отношение f /x, как видно из рисунка 1, равно тангенсу угла , который составляет секущая MN кривой y = f(x) c положительным направлением горизонтальной оси координат.
Представим себе процесс, в котором величина x, неограниченно уменьшаясь, стремится к нулю. При этом точка N будет двигаться вдоль кривой y = f(x), приближаясь к точке M, а секущая MN будет вращаться около точки M так, что при очень малых величинах x её угол наклона будет сколь угодно близок к углу наклона касательной к кривой в точке x. Следует отметить, что все сказанное относится к случаю, когда график функции y = f(x) не имеет излома или разрыва в точке x, то есть в этой точке можно провести касательную к графику функции.
Отношение y / x или, что то же самое (f(x + x) f(x)) / x, можно рассматривать при заданном x как функцию аргумента x. Эта функция не определена в точке x = 0. Однако её предел в этой точке может существовать.
Если существует предел отношения (f(x + x) – f(x)) / x в точке x = 0, то он называется производной функции y = f(x) в точке x и обозначается y или f(x):

 .
.
Нахождение производной функции y = f(x) называется дифференцированием.
Если для любого числа x из открытого промежутка (a, b) можно вычислить f(x), то функция f(x) называется дифференцируемой на промежутке (a, b).
Геометрический смысл производной заключается в том, что производная функции f(x) в точке x равна тангенсу угла наклона касательной к графику функции в этой точке.
Производная это скорость изменения функции в точке x. Из определения производной следует, что f (x) f / x, причем точность этого приближенного равенства тем выше, чем меньше x. Производная f (x) является приближенным коэффициентом пропорциональности между f и x.
Производная функции f(x) не существует в тех точках, в которых функция не является непрерывной. В то же время функция может быть непрерывной в точке x>0>, но не иметь в этой точке производной. Такую точку назовём угловой точкой графика функции или точкой излома. Графические примеры приведены на рисунке 2.

Так функция y = x не имеет производной в точке x = 0, хотя является непрерывной в этой точке.
Ниже приводится таблица производных элементарных функций.
|
f(x) |
|
f(x) |
|
f(x) |
|
|
C |
0 |
|
|
cosx |
-sinx |
|
x |
1 |
lnx |
1/x |
tgx |
1/cos2x |
|
xn |
nxn-1 |
ax |
axlna |
arcsina |
|
|
|
1/(2 |
|
|
arccosa |
- |
|
1/x |
-1 / x2 |
sinx |
cosx |
arctgx |
1/(1+x2) |
Приведем теперь основные свойства производной.
1. Если функция имеет производную в точке, то она непрерывна в этой точке.
2.
Если существует f (x)
, и С
произвольное число, то функция
 имеет производную: (Cf(x)) = Cf (x).
имеет производную: (Cf(x)) = Cf (x).
3. Если существуют f (x) и g (x), то функция S(x) = f(x) + g(x) имеет производную: S (x) = f (x) + g (x).
4. Если существуют f (x) и g (x), то функция P(x) = f(x)g(x) имеет производную: P (x) = f (x)g(x) + f(x)g (x).
5. Если существуют f (x) и g (x) и при этом g(x) 0, то функция D(x) = f(x) / g(x) имеет производную: D (x) = (f (x) g(x) f(x) g (x)) / g2(x).
В любом курсе математического анализа доказывается теорема о производной сложной функции. Мы ограничимся лишь ее формулировкой.
Пусть функция g(x) имеет производную в точке x, а функция f(z) имеет производную в точке z = g(x). Тогда сложная функция F(x) = f(g(x)) имеет в точке x производную F (x) = f (z) g (x).
Приведем примеры вычисления производной сложной функции.
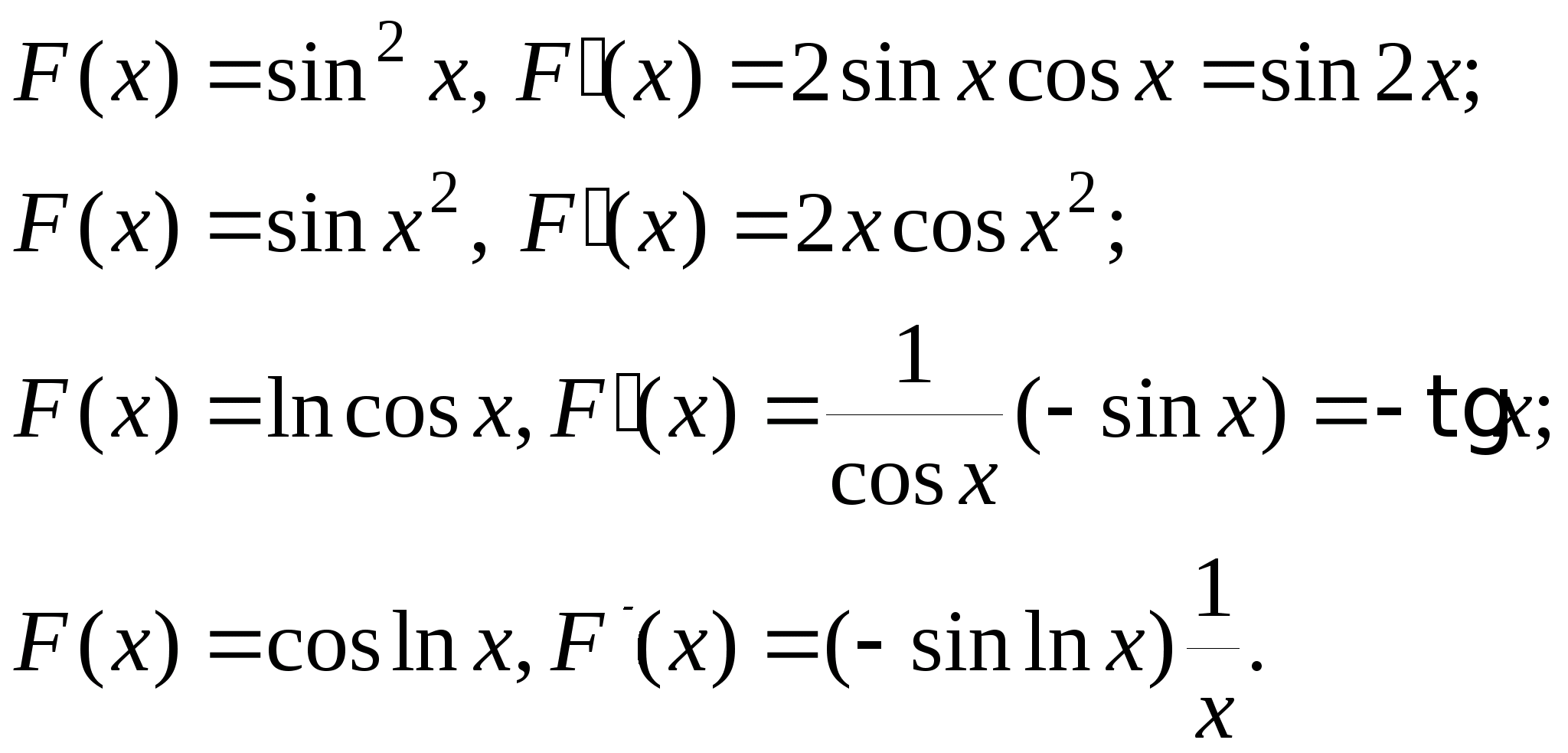
§4. Дифференциал функции
Рассмотрим две функции: y>1> = f>1>(x) и y>2> = f>2>(x), которые имеют производные f>1> (x) и f>2> (x) в каждой точке некоторой области D. Возьмем какую-либо точку x из области D и дадим аргументу приращение x. Тогда функции получат соответственно приращения y>1> = f>1>(x + x) f>1>(x) и y>2> = f>2>(x + x) f>2>(x). Из графиков, изображенных на рисунке 3, видно, что в обоих случаях приращения y>1> и y>2> можно представить в виде сумм двух слагаемых:
y>1> = (C>1> - A>1>) + (B>1> - C>1>); y>2> = (C>2> - A>2>) + (B>2> - C>2>) (1)
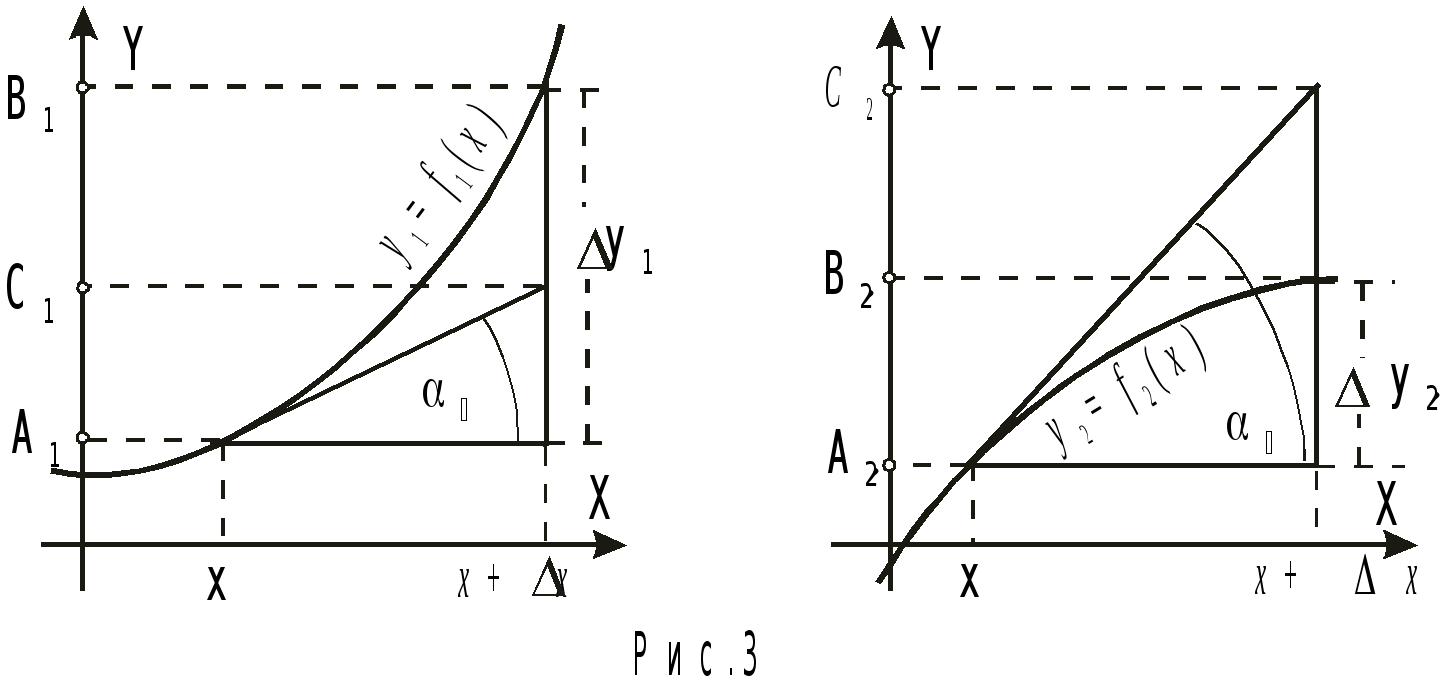
Первые слагаемые в правых частях обоих выражений (1)> >легко вычисляются из сходных формул: C>1> – A>1> = tg>1> x = f>1> (x)x; C>2> – A>2> = tg>2> x = f>2> (x)x.
 Величина
f (x) x
называется главной частью приращения
функции y = f(x)
в точке x.
(Здесь мы говорим только о функции,
имеющей в точке x
производную). Главная
часть приращения функции линейна
относительно приращения аргумента x
(можно сказать –
пропорциональна приращению x).
Это означает, что если приращение
аргумента x
уменьшить в k
раз, то и главная часть приращения
функции уменьшится в k
раз.
Величина
f (x) x
называется главной частью приращения
функции y = f(x)
в точке x.
(Здесь мы говорим только о функции,
имеющей в точке x
производную). Главная
часть приращения функции линейна
относительно приращения аргумента x
(можно сказать –
пропорциональна приращению x).
Это означает, что если приращение
аргумента x
уменьшить в k
раз, то и главная часть приращения
функции уменьшится в k
раз.
Формулы (1) можно переписать в виде:
y>1> = f>1> x + r>1>; y>2> = f>2> x + r>2>. (2)
Здесь r>1> = B>1> – C>1>; r>2>= B>2>– C>2>.
Величины r>1> и r>2> в формулах (2) при уменьшении x в k раз уменьшаются более чем в k раз, что можно видеть, сравнивая рисунки 3 и 4, и говорят, что r>1> и r>2> стремятся к нулю быстрее, чем x .

Назовем функцию (z) бесконечно малой в точке z = z>0>, если
 .
.
Пусть
функции (z)
и (z)
являются бесконечно
малыми в точке z = z>0>..
Функция (z)
называется бесконечно
малой более высокого порядка,
чем функция (z),
если
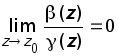 .
.
Величины
r>1>
и r>2>
в формулах (2) являются функциями аргумента
x,
бесконечно малыми в точке x = 0.
Можно показать, что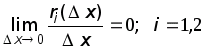 .
Это означает, что функции
r>1>(x)
и r>2>(x)
являются бесконечно
малыми функциями более высокого порядка,
чем x,
в точке x = 0.
.
Это означает, что функции
r>1>(x)
и r>2>(x)
являются бесконечно
малыми функциями более высокого порядка,
чем x,
в точке x = 0.
Таким образом приращение функции y = f(x) в точке, в которой существует её производная, может быть представлено в виде
y = f(x) x + (x),
где (x) бесконечно малая функция более высокого порядка, чем x, в точке x = 0.
Главная, линейная относительно x, часть приращения функции y = f(x), равная f (x) x, называется дифференциалом и обозначается dy:
dy = f (x) x. (3)
Если сюда подставить функцию f(x) = x, то, так как x = 1, формула (3) примет вид: dx = x. Эта формула легко истолковывается с помощью графика функции y = x, из которого видно, что приращение этой функции содержит лишь главную часть. Таким образом, для функции y = x приращение совпадает с дифференциалом. Теперь формулу дифференциала (3) можно переписать так
dy = f (x) dx.
Отсюда следует, что
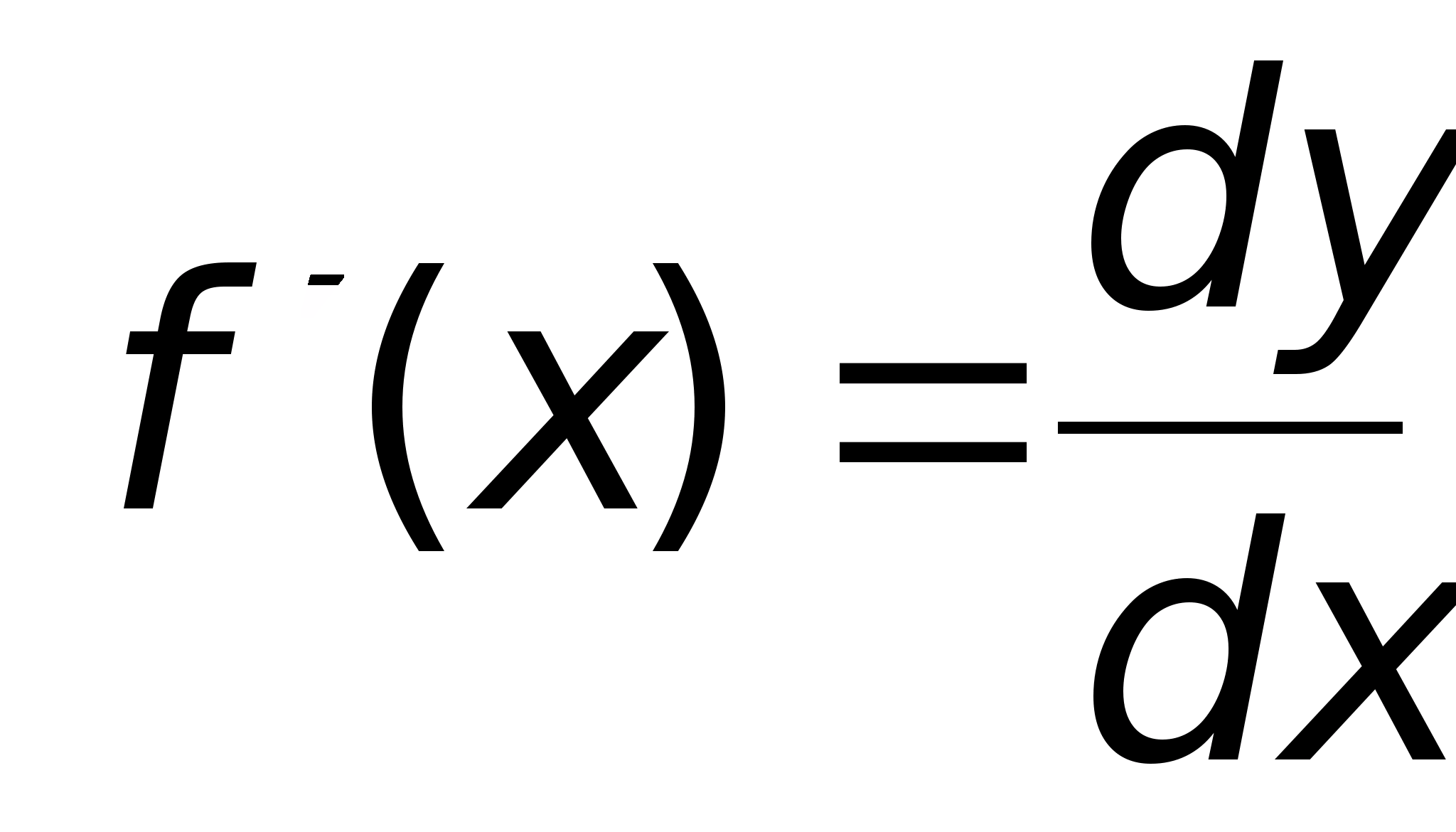 ,
,
то есть производная функции f(x) равна отношению дифференциала функции к дифференциалу аргумента x.
Очевидны следующие свойства дифференциала.
1. dC = 0 ( здесь и в следующей формуле C постоянная );
2. d(Cf(x)) = Cdf(x);
3.
Если существуют df(x)
и dg(x),
то d(f(x) + g(x)) = df(x) + dg(x),
d(f(x)g(x)) = g(x)df(x) + f(x)dg(x).
Если при этом g(x) 0,
то
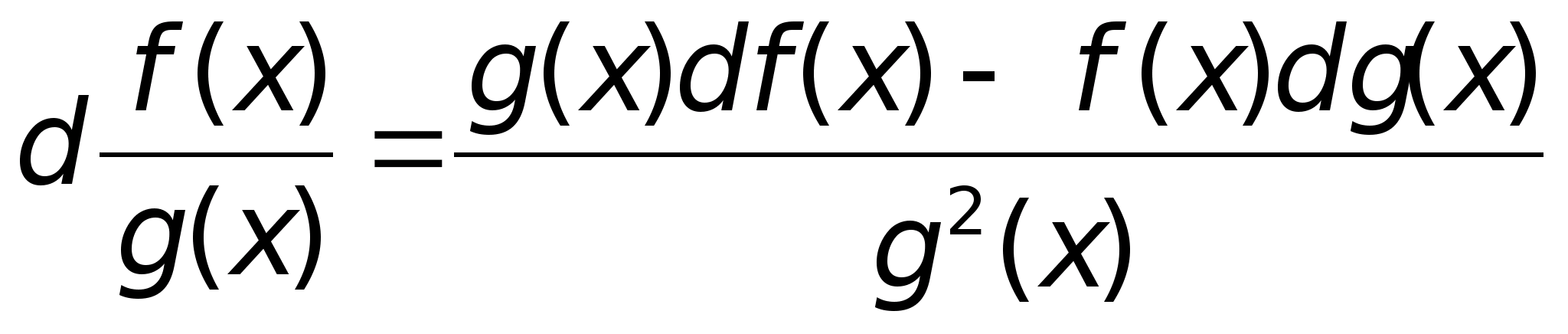
Пусть y = f(x) функция, имеющая производную в точке x, тогда dy = df(x) = f (x)dx. Если аргумент x является функцией x(t) некоторой независимой переменной t, то y = F(t) = f(x(t)) сложная функция от t, и её дифференциал вычисляется по формуле dy = F(t)dt = f (x)x (t)dt. Однако по определению дифференциала x (t)dt = dx и последняя формула преобразуется к виду: dy = f (x)dx.
Таким образом если аргумент функции y=f(x) рассматривать как функцию другого аргумента так, что равенство x = dx не выполняется, формула дифференциала функции f(x) остается неизменной. Это свойство принято называть свойством инвариантности дифференциала.
§5. Производные высших порядков.
Может оказаться что функция f(x), называемая первой производной, тоже имеет производную (f(x)). Эта производная называется второй производной функции f(x) и обозначается f(x). Если f есть координата движущейся точки и является функцией времени, то мгновенная скорость точки в момент времени t равна f(t), а ускорение равно f(t).
Вторая производная также может быть функцией, определенной на некотором множестве. Если эта функция имеет производную, то эта производная называется третьей производной функции f(x) и обозначается f(x).
Если определена n-я производная f (n)(x) и существует её производная, то она называется (n+1)-й производной функции f(x): f (n + 1)(x) = (f(n)(x)).
Все производные, начиная со второй, называются производными высших порядков.
§6. Формула Лагранжа
Если функция непрерывна на замкнутом промежутке [a, b] и дифференцируема на открытом промежутке (a, b), то можно найти такую точку c, принадлежащую промежутку (a, b), для которой справедливо равенство:
f(b) - f(a) = f(c)(b - a). (1)
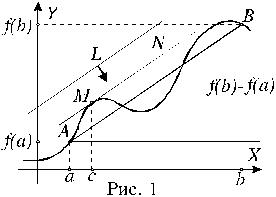




 .
.
Отсюда
сразу получается формула (1). На приведенном
рисунке видно, что могут существовать
другие точки, принадлежащие промежутку
(a, b),
в которых касательные к графику функции
f(x)
параллельны прямой MN.
Производную функции f(x),
вычисленную в любой из этих точек, можно
подставить в правую часть формулы (1)
вместо множителя
 .
.
Сформулируем теорему о монотонности функции. Если f(x) > 0 на промежутке (a;b), то на (a;b) функция f(x) возрастает. Если f(x) < 0 на промежутке (a;b), то на (a;b) функция f(x) убывает.
Докажем эту теорему. Пусть t>1 >и t>2> — любые числа из промежутка (a;b), причем t>2>>t>1>. Тогда по теореме Лагранжа можно указать такое число c из промежутка (t>1>;t>2>), для которого справедливо равенство f(t>2>) – f(t>1>) = f(c)(t>2> – t>1>). Если f(x) > 0 для всех x из промежутка (a;b), то f(c) > 0, и из условия t>2> > t>1> следует, что f(t>2>) – f(t>1>) > 0. Таким образом, возрастание функции f(x) на промежутке (a;b) доказано. Аналогично доказывается вторая часть теоремы.
§7. Необходимые и достаточные условия экстремума функции
Точка x>0> называется точкой минимума функции f(x), если можно найти такую окрестность этой точки, что для любой точки x из этой окрестности выполняется условие:
f(x) > f(x>0>).
Точка x>0> называется точкой максимума функции f(x), если можно найти такую окрестность этой точки, что для любой точки x из этой окрестности выполняется условие:
f(x) < f(x>0>).
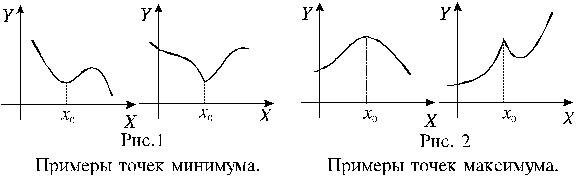
Точки максимума и минимума функции называются точками экстремума.
Сформулируем теорему о необходимом условии экстремума функции: если в точке экстремума функция f(x) имеет производную, то производная равна нулю.
Отсюда следует, что точки экстремума функции следует искать среди тех точек её области определения, где производная функции равна нулю или не существует.

Точка, в которой производная равна нулю, называется стационарной.
Точки области определения функции, в которых производная либо равна нулю, либо не существует, называются критическими.
Как было показано выше, с помощью необходимого условия нельзя определить, является ли данная точка точкой экстремума, тем более указать, какой экстремум реализуется – максимум или минимум. Для того, чтобы ответить на эти вопросы, сформулируем и докажем теорему, которая называется достаточным условием экстремума.
Пусть функция f(x) непрерывна в точке x>0>. Тогда:
1) если f(x) < 0 на (a;x>0>) и f(x) > 0 на (x>0>;b), то точка x>0> – точка минимума функции f(x);
2) если f(x) > 0 на (a;x>0>) и f(x) < 0 на (x>0>;b), то точка x>0> – точка максимума функции f(x);
Докажем первое утверждение теоремы.
Так как f(x) < 0 на (a;x>0>) и f(x) непрерывна в точке x>0>, то f(x) убывает на (a;x>0>], и для любого x(a;x>0>) выполняется условие f(x)>f(x>0>).
Так как f(x) > 0 на (x>0>;b) и f(x) непрерывна в точке x>0>, то f(x) возрастает на (x>0>;b], и для любого x(x>0>;b) выполняется условие f(x)>f(x>0>).
В результате получается, что при любом xx>0> из (a;b) выполняется неравенство f(x)>f(x>0>), то есть точка x>0> – точка минимума f(x).
Второе утверждение теоремы доказывается аналогично.
§8. Выпуклость и вогнутость функции
Пусть функция f(x) имеет производную в каждой точке промежутка (a;b). Если на промежутке (a;b) график функции f(x) расположен выше любой своей касательной, проведенной в точке этого промежутка, то функция называется вогнутой на этом промежутке (иногда говорят "выпуклой вниз").
Если на промежутке (a;b) график функции f(x) расположен ниже любой своей касательной, проведенной в точке этого промежутка, то функция называется выпуклой на этом промежутке (иногда говорят "выпуклой вверх").

Точка x>0 >называется точкой перегиба функции f(x), если в этой точке функция имеет производную и существуют два промежутка: (a;x>0>) и (x>0>;b), на одном из которых функция выпукла, а на другом вогнута.

Будем называть функцию возрастающей в точке x>0>, если она непрерывна в этой точке и возрастает в некоторой ее окрестности. Подобным образом можно определить функцию, убывающую в точке.
Приведем без доказательства важную для исследования функций теорему.
Если
 f(x) > 0
на
промежутке
(a;b),
то
на этом промежутке
функция
f(x)
вогнута.
Если
f(x) < 0
на
промежутке
(a;b),
то
на этом
промежутке
функция
f(x)
выпукла.
f(x) > 0
на
промежутке
(a;b),
то
на этом промежутке
функция
f(x)
вогнута.
Если
f(x) < 0
на
промежутке
(a;b),
то
на этом
промежутке
функция
f(x)
выпукла.
Из положительности второй производной функции на промежутке следует возрастание первой производной на этом промежутке, а это, как показано на рисунке 5, – признак вогнутой функции. Аналогичным образом иллюстрируется второе утверждение теоремы.

Если x>0> – точка перегиба функции f(x), то f(x>0>) = 0.
Приведем другую формулировку достаточных условий экстремума функции.
Если в точке x>0 >выполняются условия:
1) f(x>0>) = 0; f(x>0>) < 0, тогда x>0 > – точка максимума;
2) f(x>0>) = 0; f(x>0>) > 0, тогда x>0 > – точка минимума;
3) f(x>0>) = 0; f(x>0>) = 0, тогда вопрос о поведении функции в точке остается открытым. Здесь может быть экстремум, например в точке x>0 >= 0 у функции y = x4, но может его не быть, например в точке x>0 >= 0 у функции y = x5. В этом случае для решения вопроса о наличии экстремума в стационарной точке можно использовать достаточные условия экстремума, приведенные выше.
Рассмотрим пример из микроэкономики.
В количественной теории полезности предполагается, что потребитель может дать количественную оценку (в некоторых единицах измерения) полезности любого количества потребляемого им товара.
Это означает существование функции полезности TU аргумента Q –количества купленного товара. Введём понятие предельной полезности, как добавочной полезности, прибавляемой каждой последней порцией товара. Далее построим двумерную систему координат, откладывая по горизонтальной оси
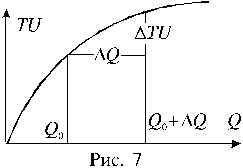
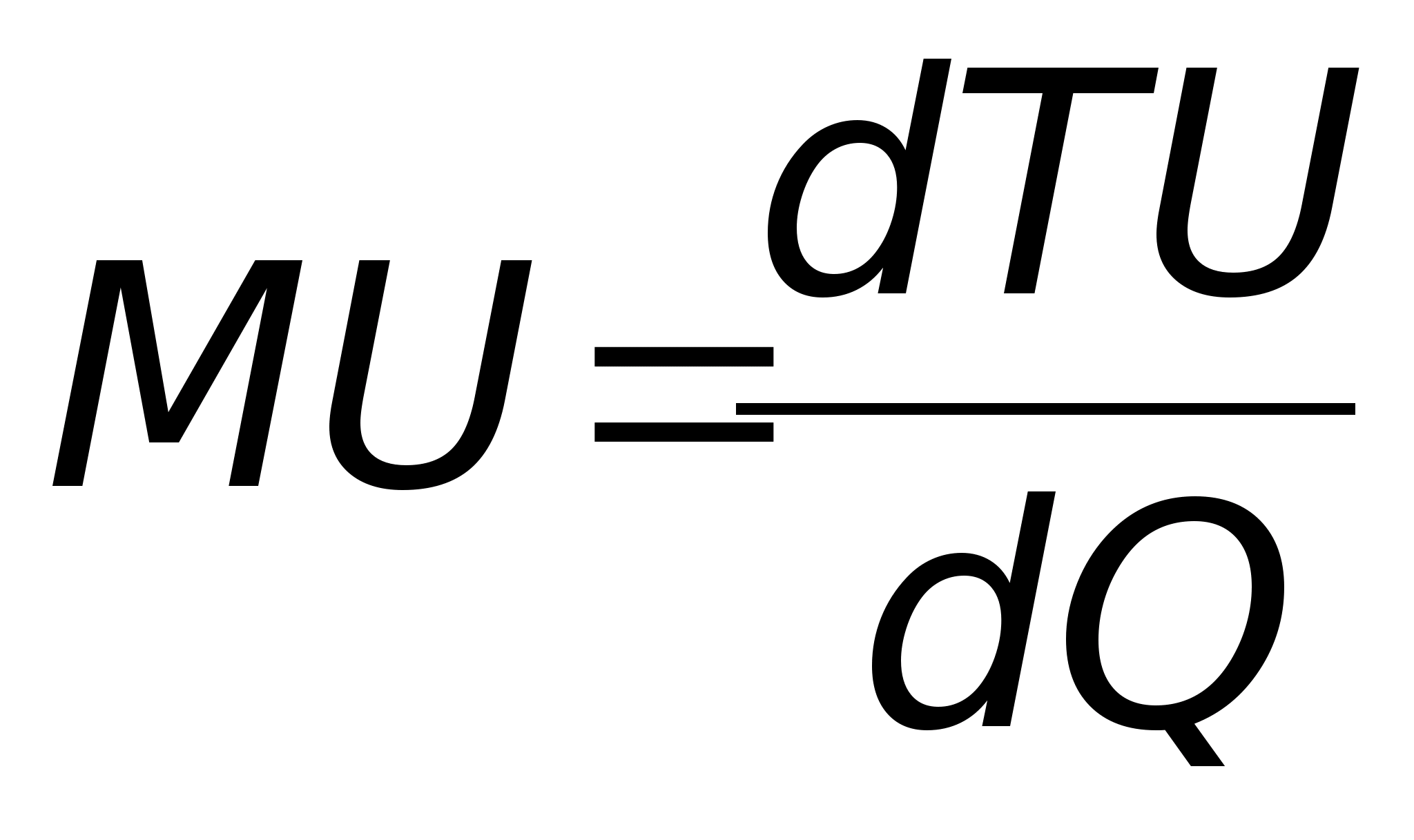 .
.
Это означает, что предельная полезность равна производной функции полезности TU(Q). Закон убывающей предельной полезности сводится к уменьшению этой производной с ростом величины Q. Отсюда следует выпуклость графика функции TU(Q). Понятие функции полезности и представление предельной полезности в виде производной этой функции широко используется в математической экономике.
§9. Неопределенный интеграл.
Функция F(x) называется первообразной для функции f(x) на промежутке (a;b), если для всех x(a;b) выполняется равенство F(x) = f(x).
Например, для функции x2 первообразной будет функция x3/3.
Если
для F(x)
установлено равенство dF(x) = f(x)dx,
то F(x)
первообразная для f(x),
так как
 .
.
Рассмотрим две теоремы, которые называются теоремами об общем виде всех первообразных данной функции.
Теорема 1. Если F(x) – первообразная для f(x) на (a;b), то F(x) + C, где C – число, тоже первообразная для f(x) на (a;b).
Доказательство.
(F + C) = F + C = f + 0 = f
По определению F + C первообразная для f.
Прежде чем рассмотреть теорему 2, докажем две вспомогательные теоремы.
Если функция g(x) постоянна на (a;b), то g(x) = 0.
Доказательство.
Так как g(x) = C, справедливы равенства: g(x) = C = 0 (здесь, как и ниже, через C обозначено произвольно выбранное число).
Если g(x) = 0 при всех x(a;b), то g(x) = C на (a;b).
Доказательство.
Пусть g(x) = 0 во всех точках (a;b). Зафиксируем точку x>1>(a;b). Тогда для любой точки x(a;b) по формуле Лагранжа имеем
g(x) – g(x>1>) = g()(x – x>1>)
Так как (x; x>1>), а точки x и x>1> принадлежат промежутку (a;b), то g() = 0, откуда следует, что g(x) – g(x>1>)=0, то есть g(x) = g(x>1>)=const.
Теорема 2. Если F(x) есть первообразная для f(x) на промежутке (a;b), а G(x) – другая первообразная для f(x) на (a;b), то G = F + C, где C – число.
Доказательство.
Возьмем
производную от разности G – F:
(G – F) = G – F =
= f – f = 0.
Отсюда следует: G – F = C,
где C
число, то есть G = F + C.
Множество всех первообразных для функции f(x) на промежутке (a;b) называется неопределенным интегралом и обозначается >>f(x)dx. Если F(x) – первообразная для f(x), то >>f(x)dx = F(x) + C, где C – произвольное число.
Вычисление неопределенного интеграла от заданной функции называется интегрированием.
Из определения неопределенного интеграла следует, что каждой формуле дифференциального исчисления F(x) = f(x) соответствует формула >>f(x) dx = F(x) + C интегрального исчисления. Отсюда получается таблица неопределенных интегралов:
|
1) >> dx = x + C; |
7) >>> >cosx dx = sinx + C; |
|
2)
>> xdx= |
8)
|
|
3)
|
9)
|
|
4) exdx =ex+C; |
10)
|
|
5) >> axdx =axlog>a>e+C (1) ; |
11)
|
|
6) >>> >sinx dx=-cosx + C; |
12)
|
Неопределенный интеграл обладает следующими свойствами:
|
1) ( >>f(x) dx )=f(x); |
4) >>d f(x)=f(x)+C ; |
|
2) >>f (x) dx= f(x)+C ; |
5) kf(x)dx=kf(x) dx; |
|
3) d >>f(x) dx= f(x)dx; |
6) >>(f(x)+g(x))dx=>> f(x) dx+>>g(x) dx ; |
(a 0). |
Все эти свойства непосредственно следуют из определения.
§10. Замена переменной в неопределенном интеграле
Если функция f(x) непрерывна, а функция (t) имеет непрерывную производную (t), то имеет место формула
>> f((t))(t) dt = >>> >f(x) dx, где x = (t).
Можно привести примеры вычисления интеграла с помощью перехода от левой части к правой в этой формуле, а можно привести примеры обратного перехода.
Примеры. 1. I = >>> >cos(t3) t2 dt. Пусть t3 = x, тогда dx = 3t2dt или t2dt = dx/3.
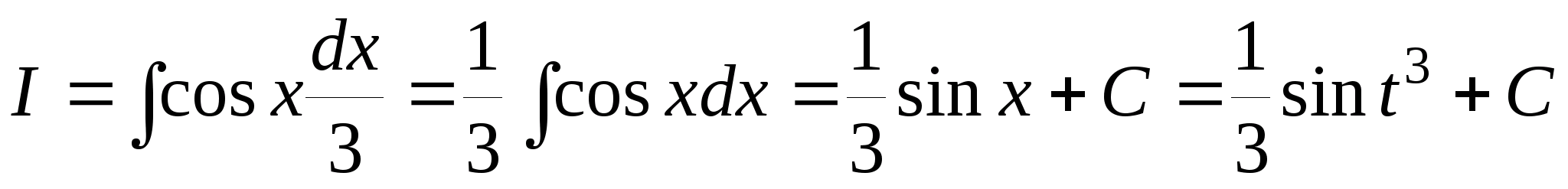 .
.
2.
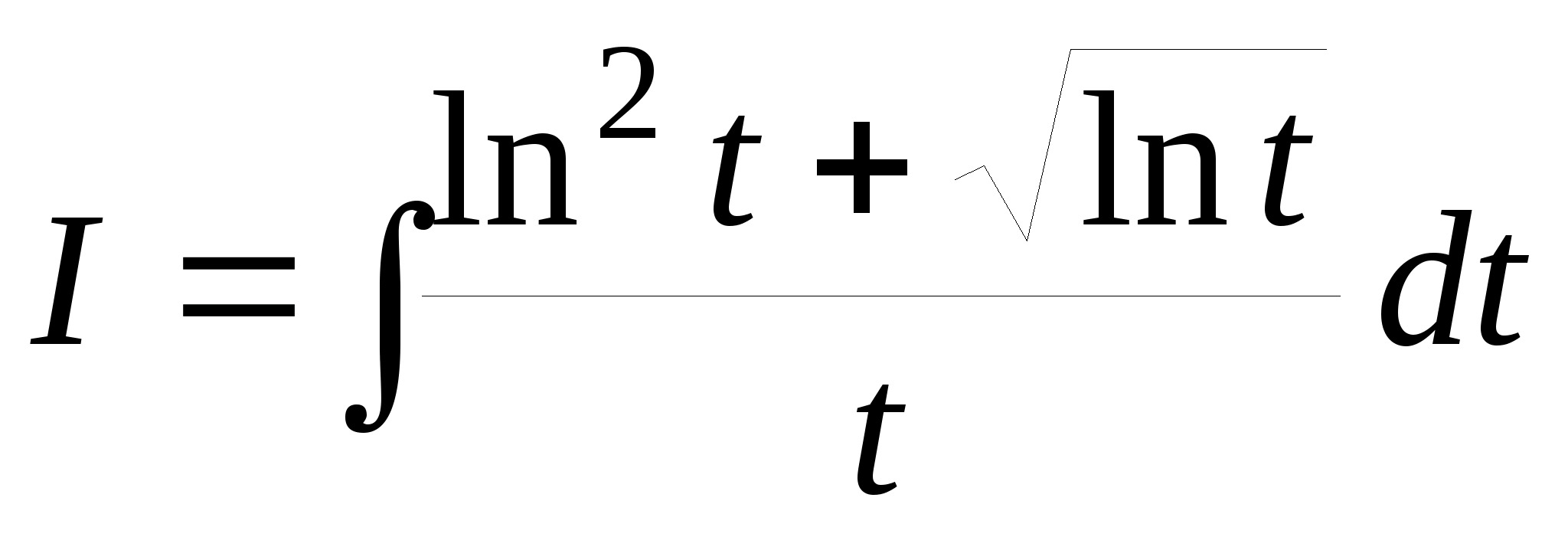 .
Пусть ln
t = x,
тогда dx = dt/t.
.
Пусть ln
t = x,
тогда dx = dt/t.

3.
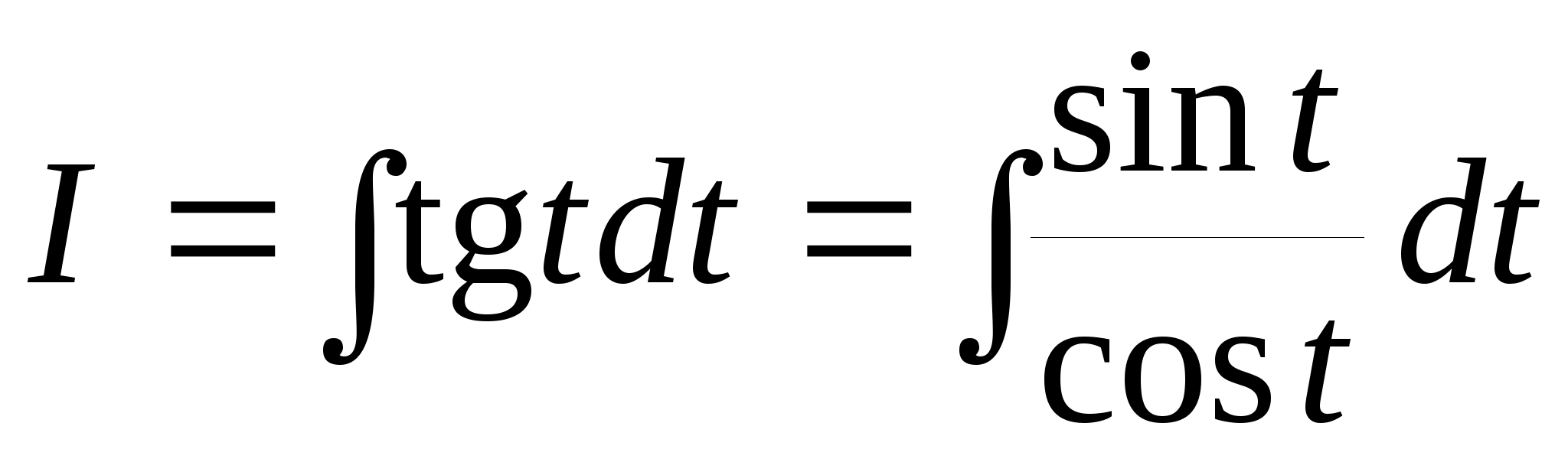 .
Пусть x = cos
t,
тогда dx = - sint dt,
и
.
Пусть x = cos
t,
тогда dx = - sint dt,
и
 .
.
4.
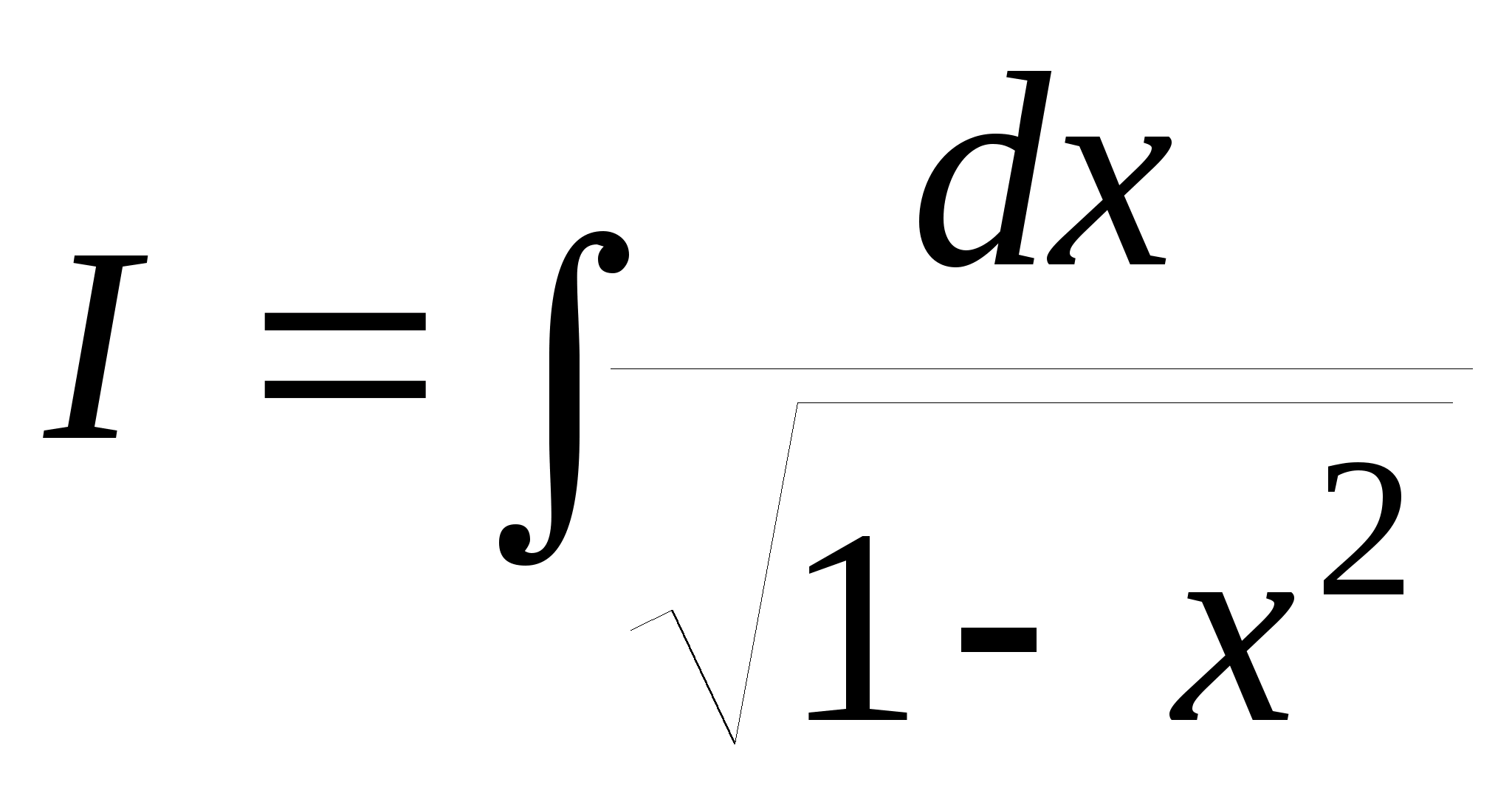 .
Пусть x = sin t,
тогда dx = cos
dt,
и
.
Пусть x = sin t,
тогда dx = cos
dt,
и
 .
.
§11. Формула интегрирования по частям
Пусть u(x) и v(x) — дифференцируемые на некотором промежутке функции. Тогда
(uv) = uv + vu
Отсюда следует
>>> >(uv)dx => >>>> >(uv + vu> >)dx = >>> >uv dx + >>> >vu dx
или
>> uv> >dx = uv – >> uv dx .
Отсюда следует формула, которая называется формулой интегрирования по частям:
>>> >u(x)dv(x) = u(x) v(x) – >>> >v(x)du(x)
Приведем примеры применения формулы интегрирования по частям.
Примеры. 1. I = >>> >x cosx dx. Пусть u = x; dv = cosx dx, тогда du = dx; v = sinx. Отсюда по формуле интегрирования по частям получается:
I = x sinx – >>> >sinx dx = x sinx + cosx + C.
2.
I = >>> >(x2 – 3x + 2) e5xdx.
Пусть
x2 – 3x + 2 = u;
e5xdx = dv.
Тогда
du = (2x – 3) dx;
 .
.
 .
.
К
последнему интегралу применим метод
интегрирования по частям, полагая
2x - 3 = u;
e5xdx = dv.
Отсюда следует: du = 2dx;
 ,
и окончательно получаем:
,
и окончательно получаем:
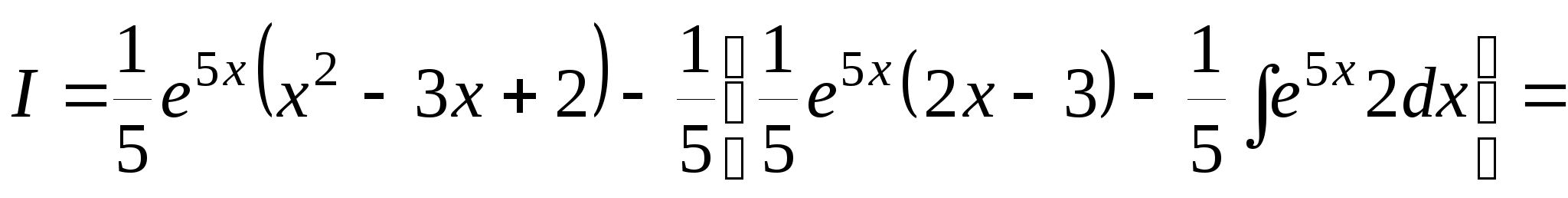
 .
.
3.
 ;
;
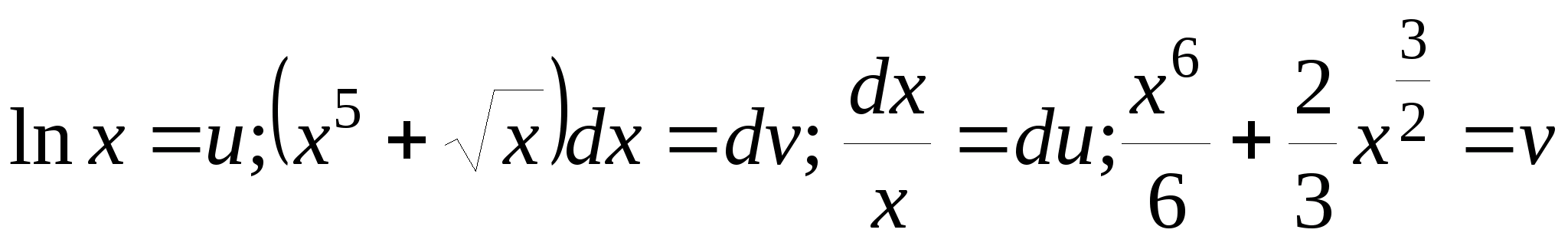 ;
;


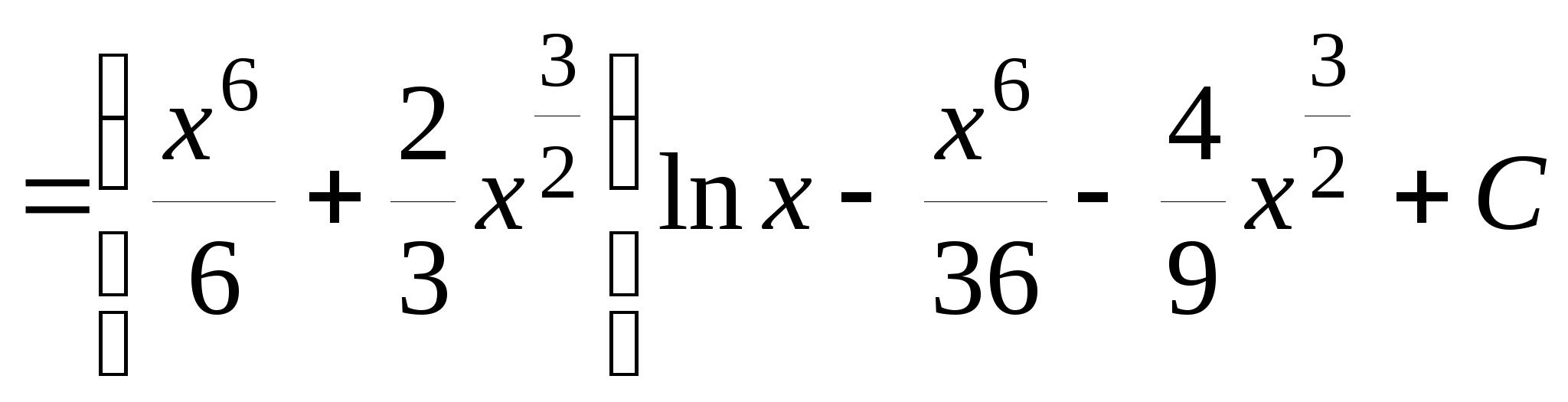 .
.
В заключение покажем метод вычисления неопределенного интеграла, стоящего в приведенной выше таблице под номером 12:
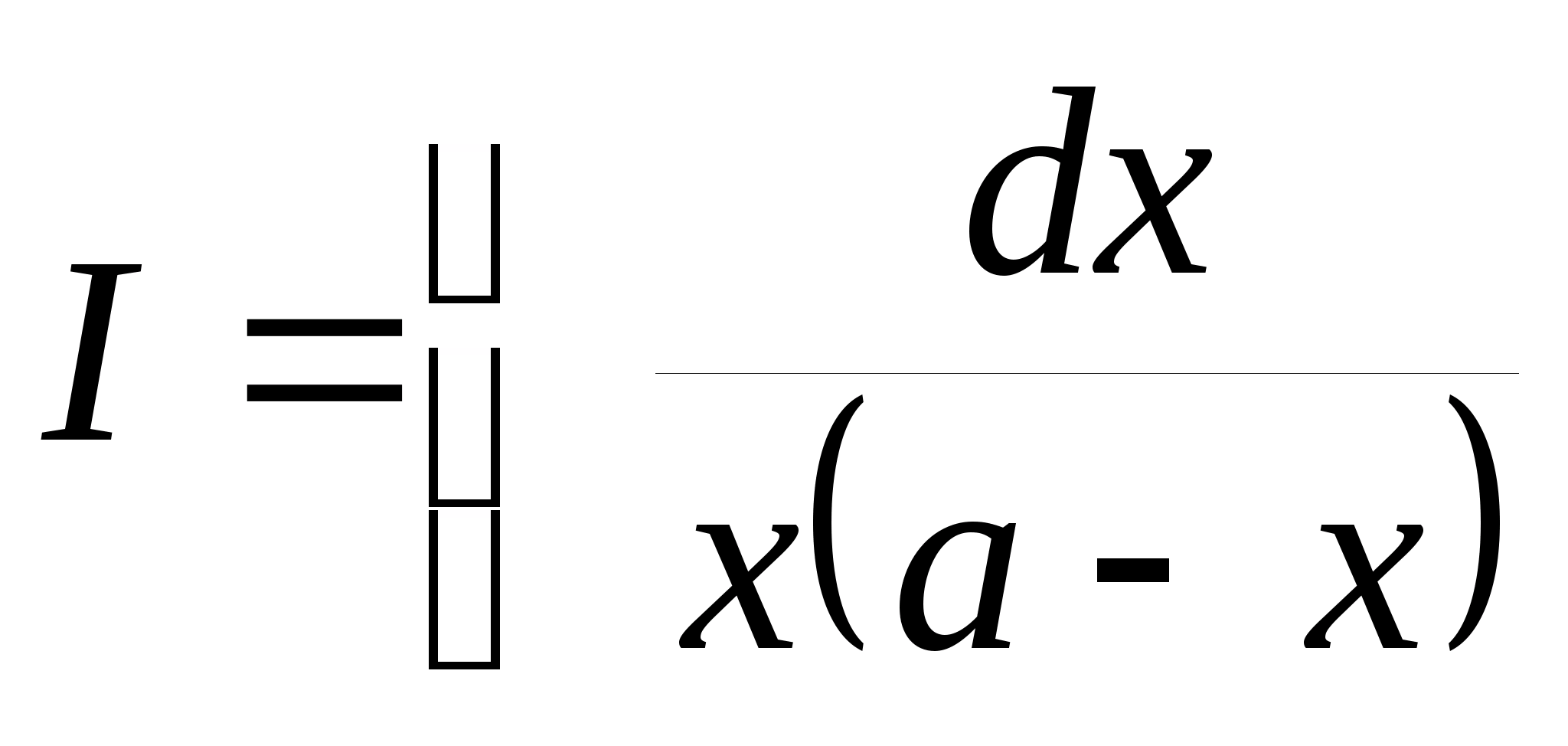 .
.
Представим
дробь
 в виде суммы двух дробей:
в виде суммы двух дробей:
 и
и
 ,
и попытаемся найти неизвестные величины
параметров A
и
B.
Из равенства
,
и попытаемся найти неизвестные величины
параметров A
и
B.
Из равенства
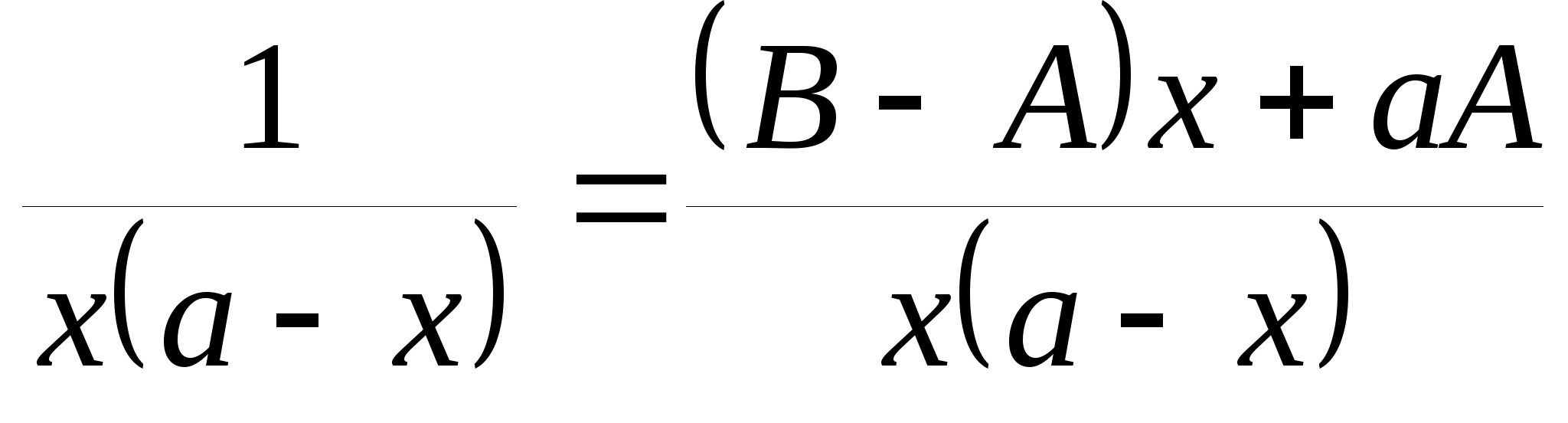 получим систему уравнений
получим систему уравнений

с
решением
 .
Отсюда следует:
.
Отсюда следует:
 .
.
Полученный интеграл в обиходе обычно называют “высоким логарифмом”. Метод, которым он был найден, называется методом “неопределенных коэффициентов”. Этот метод применяется при вычислении интегралов от дробей с числителем и знаменателем в виде многочленов.
§12. Определенный интеграл
Пусть
на промежутке [a;b]
задана функция f(x).
Будем считать функцию непрерывной, хотя
это не обязательно. Выберем на промежутке
[a;b]
произвольные числа x>1>, x>2>, x>3>, , x>n>>-1>,
удовлетворяющие условию:
a<
x>1>,<
x>2><<
x>n>>-1>,<b.
Эти числа разбивают промежуток [a;b]
на n
более мелких промежутков:
[a;x>1>], [x>1>;x>2>], [x>n>>-1>;b].
На каждом из этих промежутков выберем
произвольно по одной точке:
c>1>[a;x>1>], c>2>[x>1>;x>2>], c>n>[x>n>>-1>;b].
Введем обозначения: x>1> = x>1 >– a; x>2> = x>2 >– x>1>; x>n> = b – x>n->>1>.
Составим сумму:
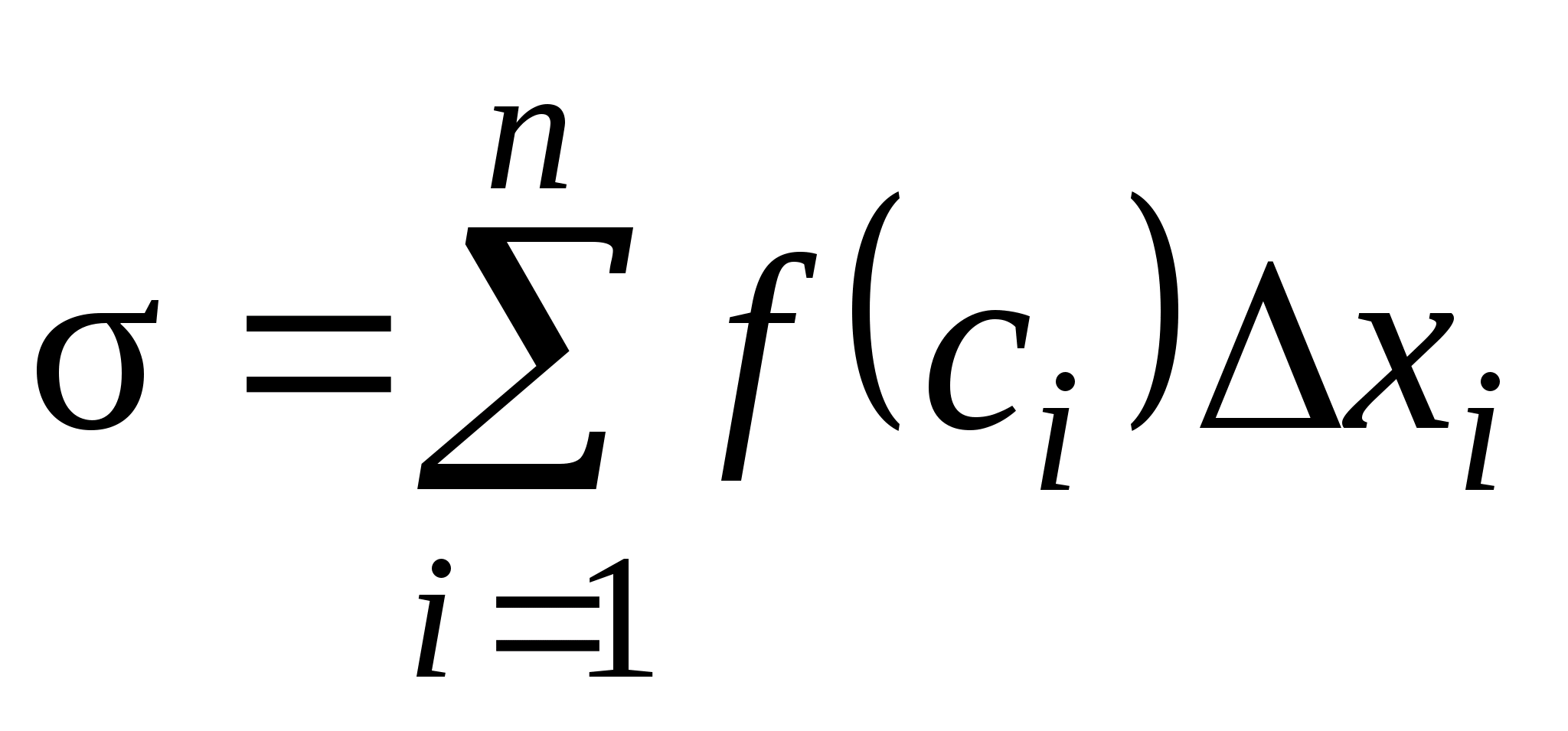 .
.

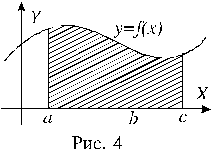
Каждое слагаемое интегральной суммы представляет собой площадь прямоугольника, покрытого штриховкой на рисунке 1.
Введем обозначение: = max(x>i>), i = 1, 2, n.. Величину иногда называют параметром разбиения.
Рассмотрим процесс, при котором число точек разбиения неограниченно возрастает таким образом, что величина стремится к нулю. Определенным интегралом

от
функции
 по промежутку [a;b]
называется предел, к которому стремится
интегральная сумма при этом процессе,
если предел существует:
по промежутку [a;b]
называется предел, к которому стремится
интегральная сумма при этом процессе,
если предел существует:
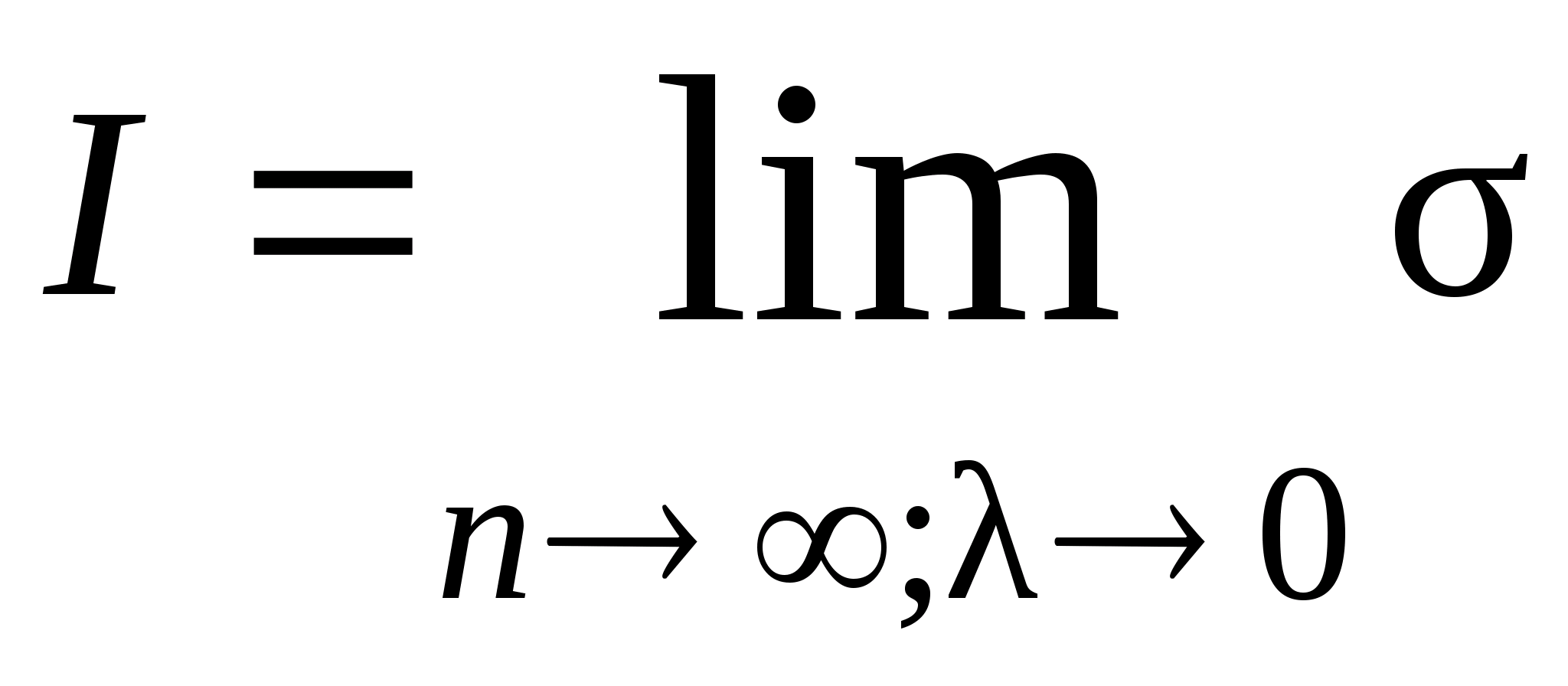 .
.
Если такой предел существует, то он не зависит от первоначального разбиения промежутка [a;b] и выбора точек c>i>.

Рассмотрим фигуру, ограниченную графиком непрерывной, неотрицательной на промежутке [a;b] функции f(x), отрезком [a;b] оси X, и прямыми x = a; x = b. Такую фигуру называют криволинейной трапецией. На рисунке 2 криволинейная трапеция выделена штриховкой. Площадь S этой трапеции определяется формулой
 .
.

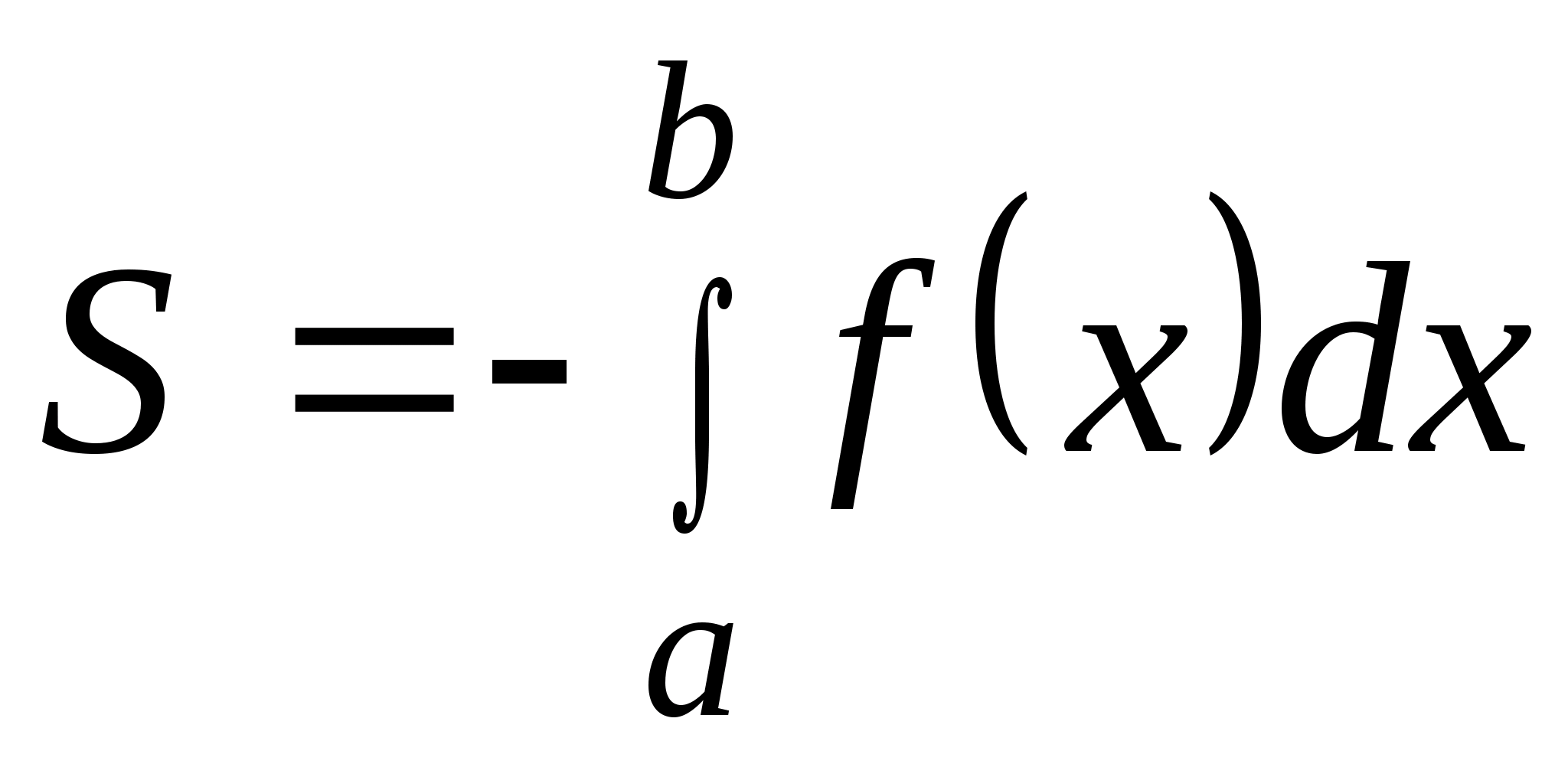 .
.
Перечислим свойства определенного интеграла:
1)
 (здесь k
произвольное число);
(здесь k
произвольное число);
2)
 ;
;
3)
 ;
;
4)
Если c[a;b],
то
 .
.
Из
этих
свойств следует, например,
что
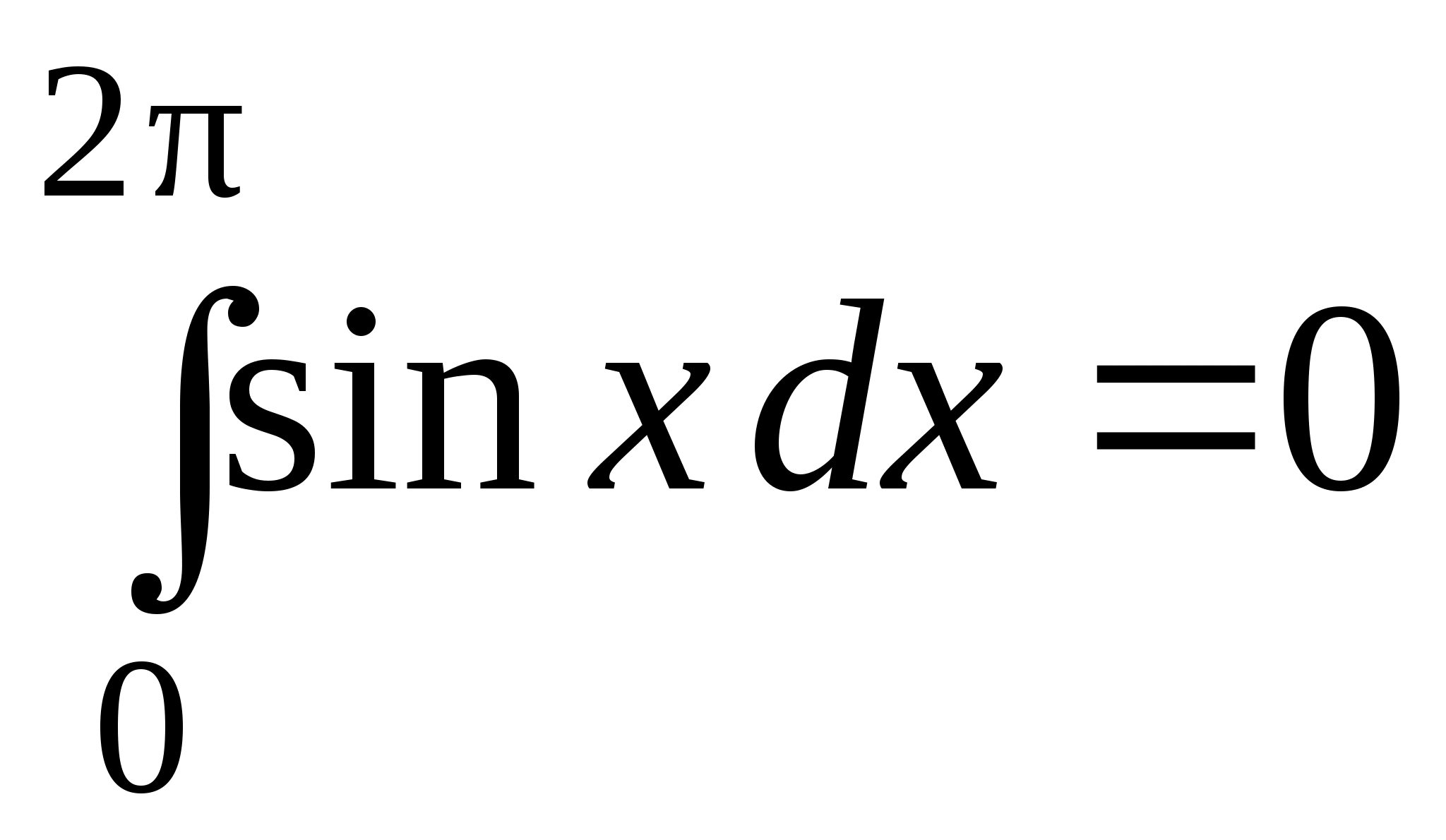 .
.
Все приведенные выше свойства непосредственно следуют из определения определенного интеграла.
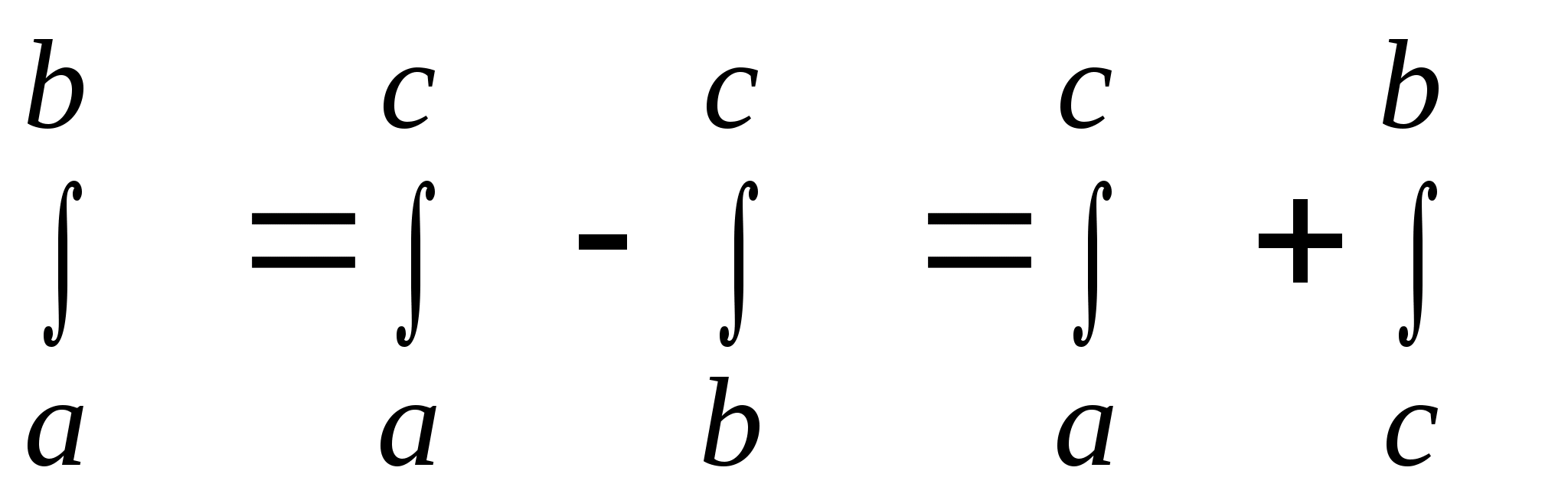 .
.
§13. Определенный интеграл как функция верхнего предела
Пусть функция f(t) определена и непрерывна на некотором промежутке, содержащем точку a. Тогда каждому числу x из этого промежутка можно поставить в соответствие число
 ,
,
I(x) = I(x + x) – I(x) =

 .
.
Как показано на рисунке 1, величина последнего интеграла в формуле для приращения I(x) равна площади криволинейной трапеции, отмеченной штриховкой. При малых величинах x (здесь, так же как и везде в этом курсе, говоря о малых величинах приращений аргумента или функции, имеем в виду абсолютные величины приращений, так как сами приращения могут быть и положительными и отрицательными) эта площадь оказывается приблизительно равной площади прямоугольника, отмеченного на рисунке двойной штриховкой. Площадь прямоугольника определяется формулой f(x)x. Отсюда получаем соотношение
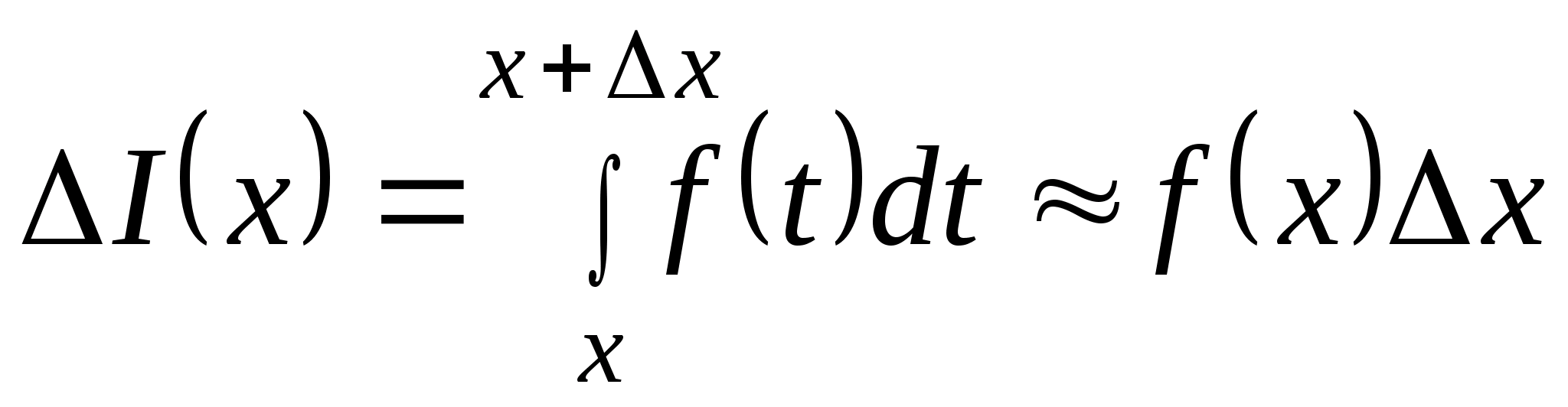 .
.
В последнем приближенном равенстве точность приближения тем выше, чем меньше величина x.
Из сказанного следует формула для производной функции I(x):
 .
.
Производная
определенного интеграла по верхнему
пределу в точке x
равна значению
подынтегральной функции в точке x.
Отсюда следует, что функция
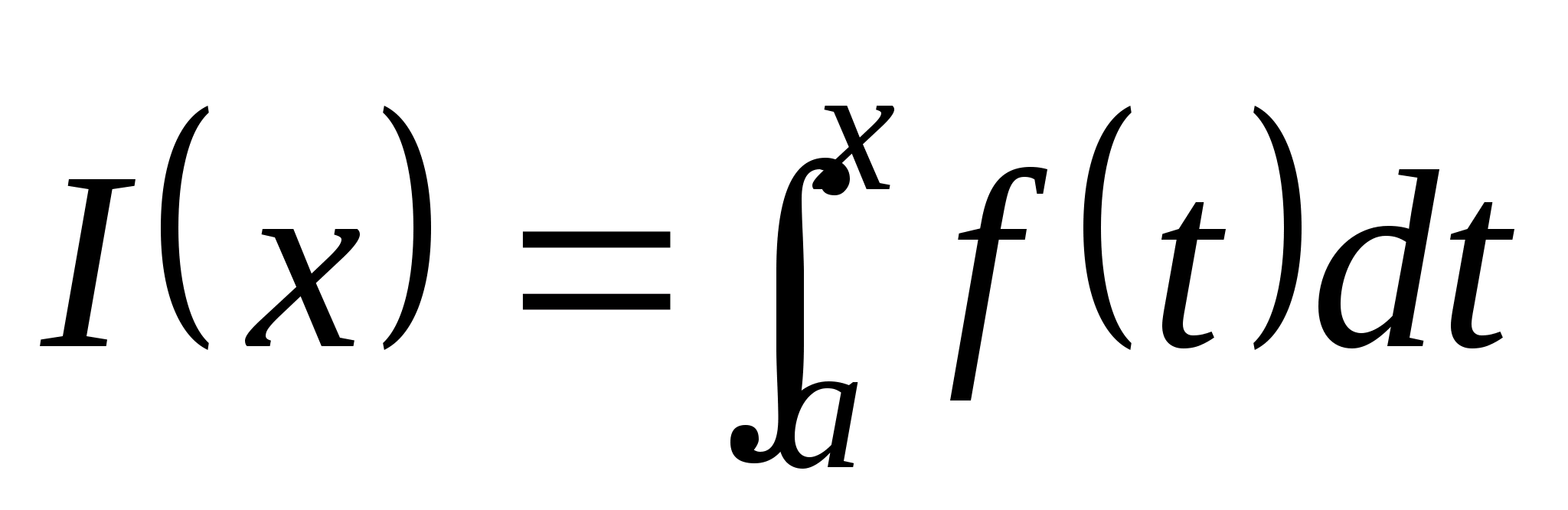 является первообразной для функции
f(x),
причем такой первообразной, которая
принимает в точке x = a
значение, равное нулю. Этот факт дает
возможность представить определенный
интеграл в виде
является первообразной для функции
f(x),
причем такой первообразной, которая
принимает в точке x = a
значение, равное нулю. Этот факт дает
возможность представить определенный
интеграл в виде
 . (1)
. (1)
Пусть F(x) тоже является первообразной для функции f(x), тогда по теореме об общем виде всех первообразных функции I(x) = F(x) + C, где C — некоторое число. При этом правая часть формулы (1) принимает вид
I(x) – I(a) = F(x) + C – (F(a) +C) = F(x) – F(a). (2)
Из формул (1) и (2) после замены x на b следует формула для вычисления определенного интеграла от функции f(t) по промежутку [a;b]:
 ,
,
которая называется формулой Ньютона-Лейбница. Здесь F(x) — любая первообразная функции f(x).
Для
того, чтобы вычислить определенный
интеграл от функции f(x)
по промежутку [a;b],
нужно найти какую-либо первообразную
F(x)
функции f(x)
и подсчитать разность значений
первообразной в точках b
и a.
Разность этих значений первообразной
принято обозначать символом  .
.
Приведем примеры вычисления определенных интегралов с помощью формулы Ньютона-Лейбница.
Примеры.
1.
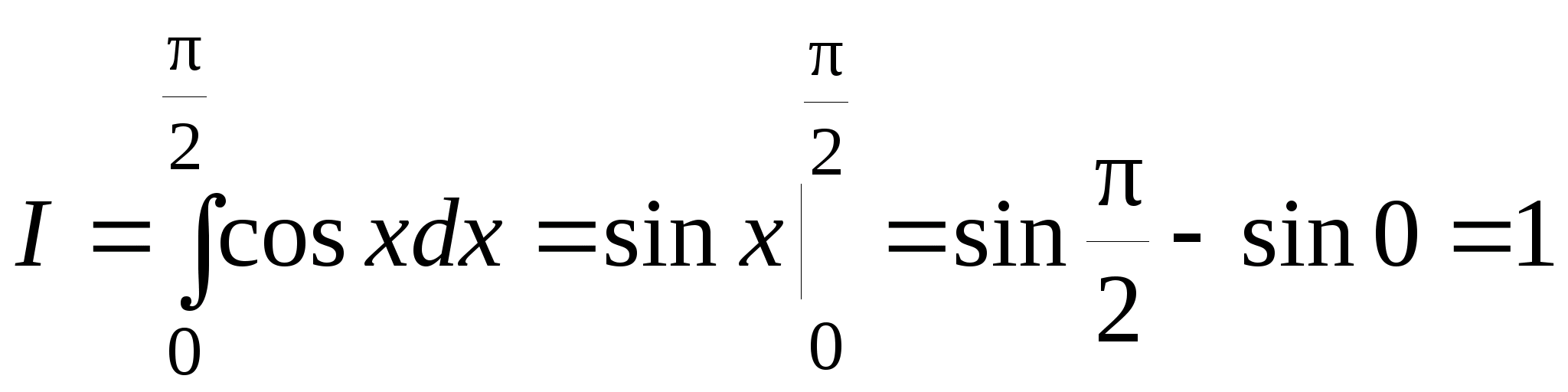 .
.
2.
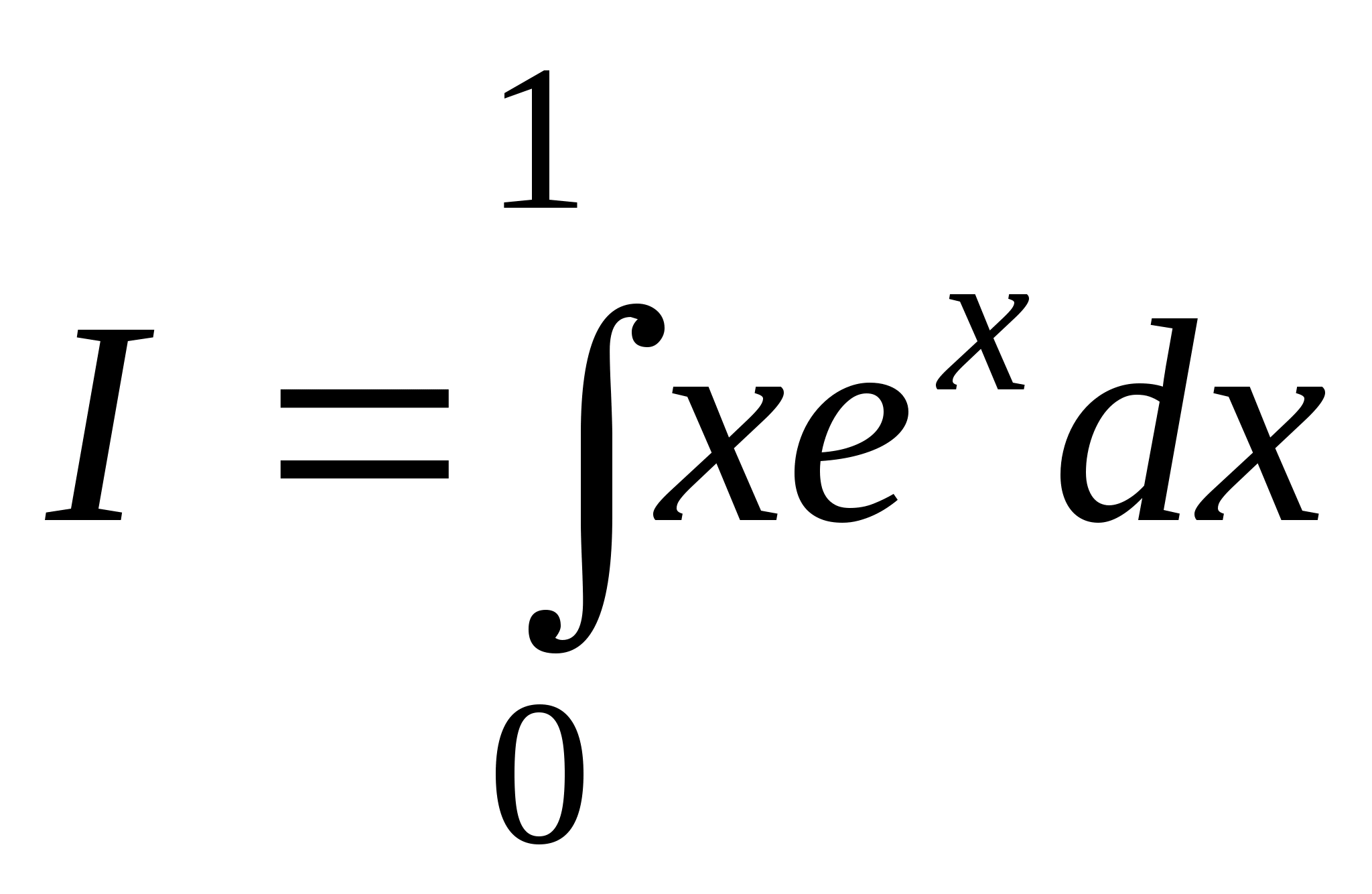 .
.
Сначала
вычислим неопределенный интеграл от
функции f(x) = xex.
Используя метод интегрирования по
частям, получаем:
 .
В качестве первообразной функции f(x)
выберем функцию ex(x – 1)
и применим формулу Ньютона-Лейбница:
.
В качестве первообразной функции f(x)
выберем функцию ex(x – 1)
и применим формулу Ньютона-Лейбница:
I = ex(x – 1) = 1.
= 1.
При вычислении определенных интегралов можно применять формулу замены переменной в определенном интеграле:
 .
.
Здесь и определяются, соответственно, из уравнений () = a; () = b, а функции f, , должны быть непрерывны на соответствующих промежутках.
Пример: .
.
Сделаем замену: ln x = t или x = et, тогда если x = 1, то t = 0, а если x = e, то t = 1. В результате получим:
 .
.
При замене переменной в определенном интеграле не нужно возвращаться к исходной переменной интегрирования.
§14. Несобственные интегралы с бесконечными пределами
Если положить промежуток интегрирования бесконечным, то приведенное выше определение определенного интеграла теряет смысл, например, потому что невозможно осуществить условия n; 0 для бесконечного промежутка. Для такого интеграла требуется специальное определение.
Пусть
функция y = f(x)
определена и непрерывна
на полубесконечном промежутке [a;),
тогда несобственным
интегралом с бесконечным пределом
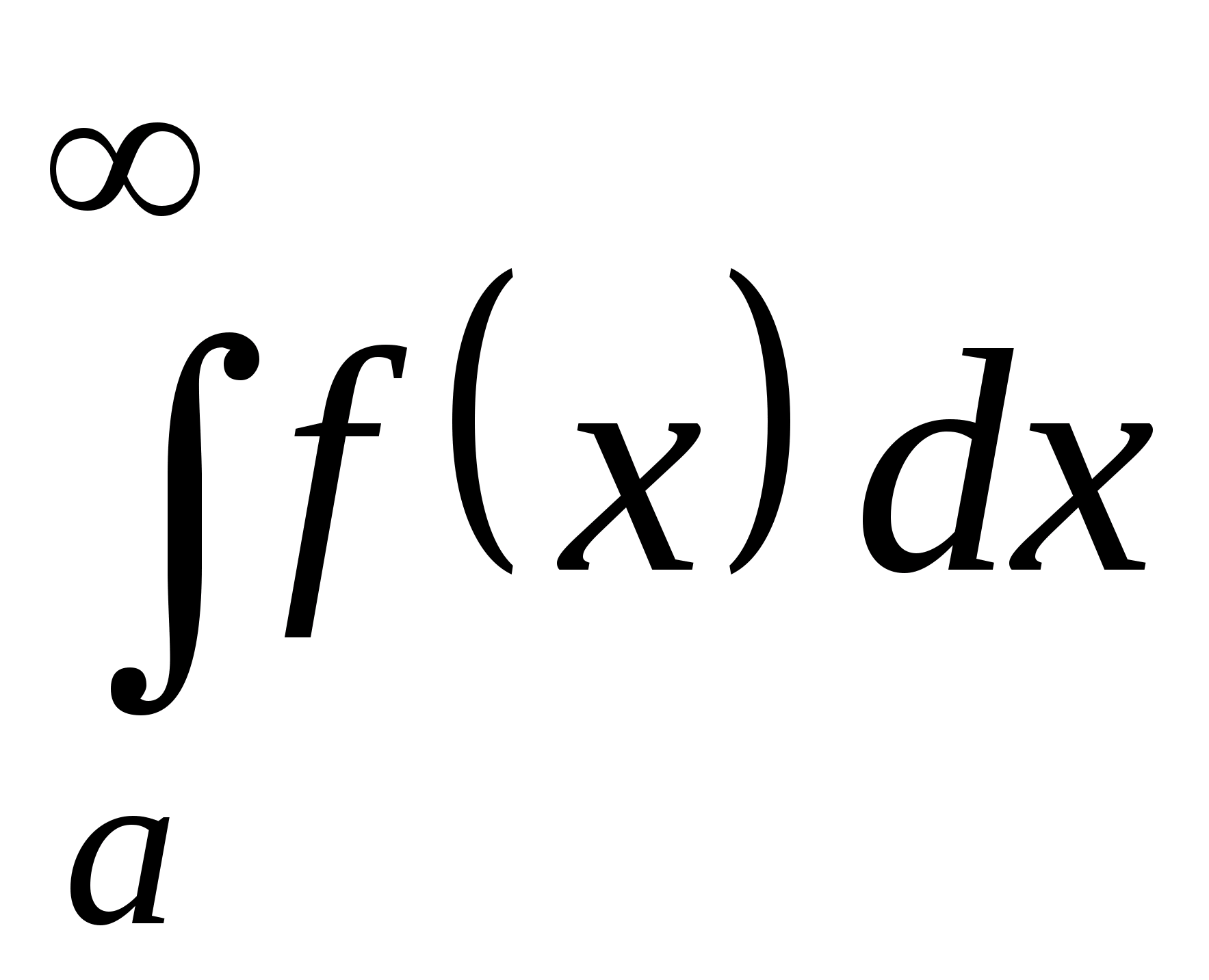 называется
называется
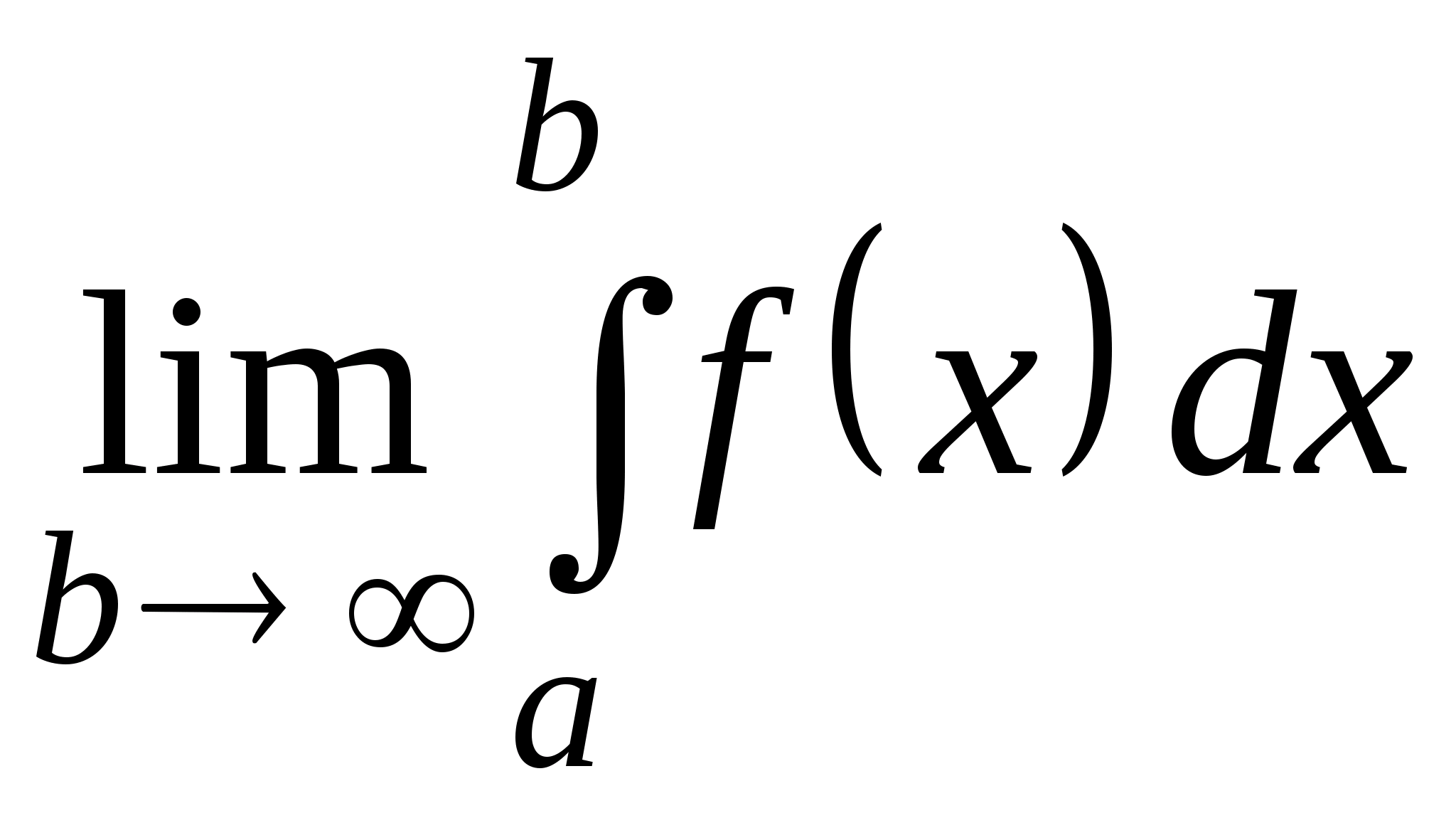 ,
если предел существует. Если этот предел
не существует, то не существует и
несобственный интеграл. В этом случае
принято говорить, что несобственный
интеграл расходится.
При существовании предела говорят, что
несобственный интеграл сходится.
,
если предел существует. Если этот предел
не существует, то не существует и
несобственный интеграл. В этом случае
принято говорить, что несобственный
интеграл расходится.
При существовании предела говорят, что
несобственный интеграл сходится.
Аналогично
 и
и
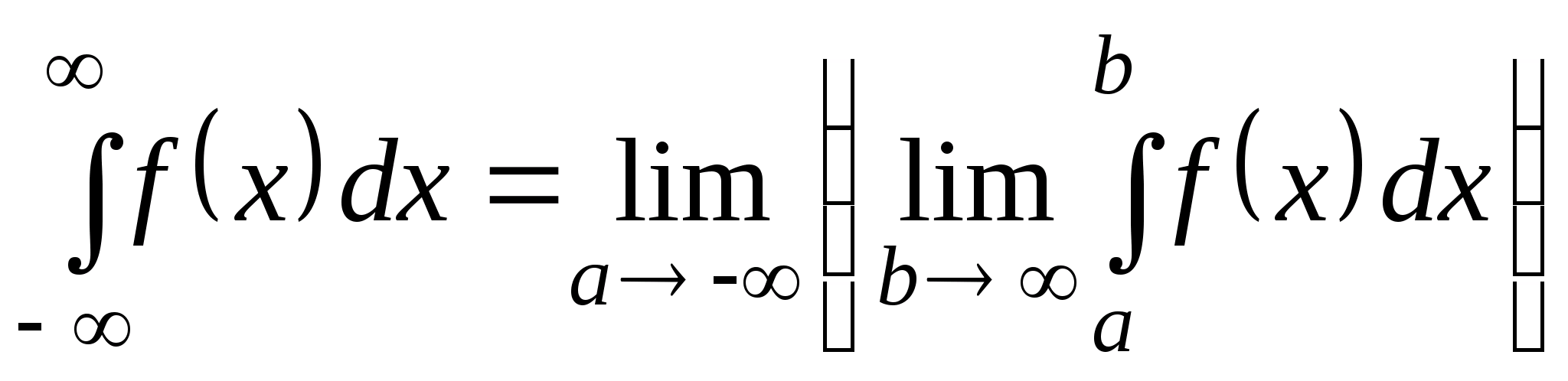 .
.
Примеры:
1.
 .
Очевидно:
.
Очевидно:
 ,
откуда следует
,
откуда следует
 .
.
2.
 ;
этот предел не существует, следовательно,
не существует или расходится интеграл
I.
;
этот предел не существует, следовательно,
не существует или расходится интеграл
I.
3.
 ;
здесь предел также не существует, и
интеграл расходится.
;
здесь предел также не существует, и
интеграл расходится.
Упражнения
1. Найти производные от следующих функций:
|
1) |
|
2) |
|
|
3) |
|
3) |
|
|
5) |
|
6) |
|
|
7) |
|
8) |
|
|
9) |
|
10) |
|
|
11) |
|
12) |
|
|
13) |
|
14) |
|
|
15) |
|
16) |
|


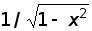
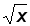


 (1);
(1); ;
; ;
;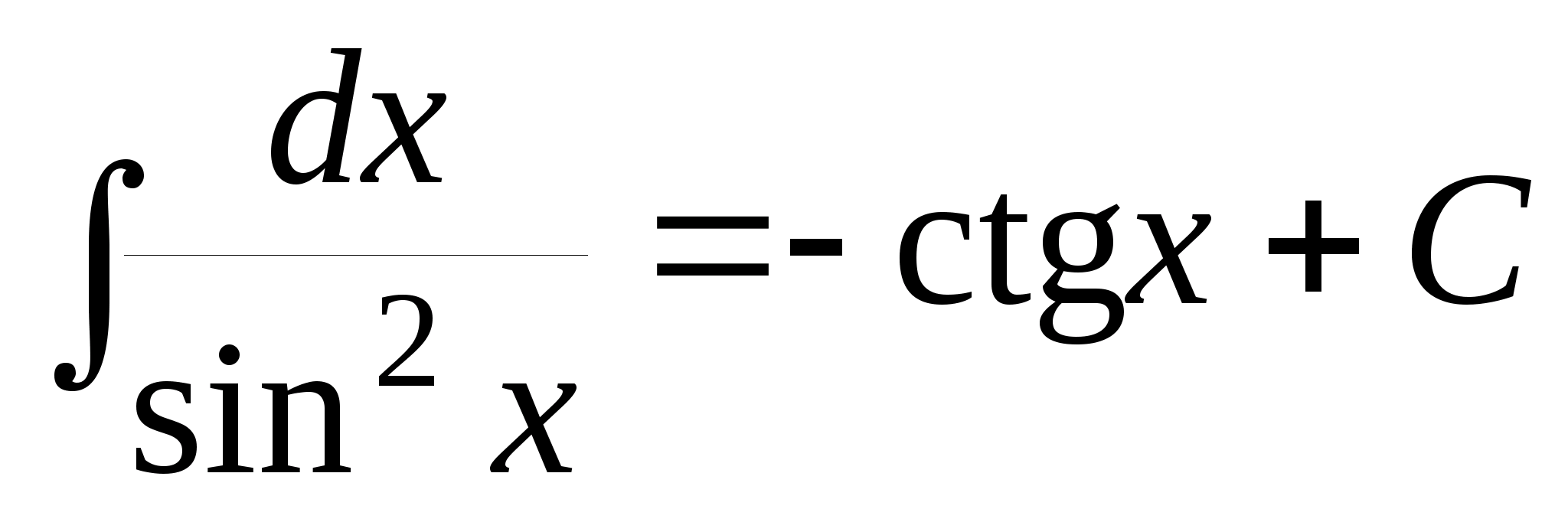 ;
;
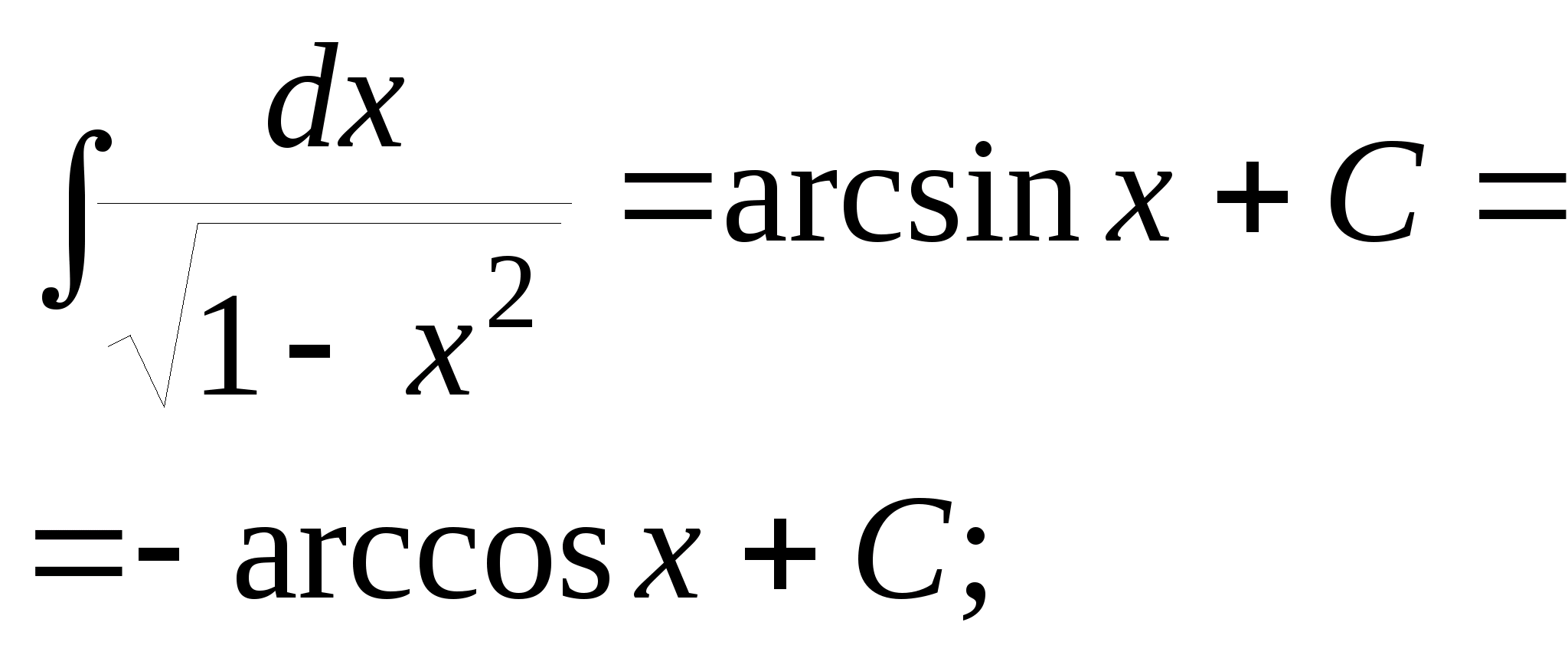
 .
.
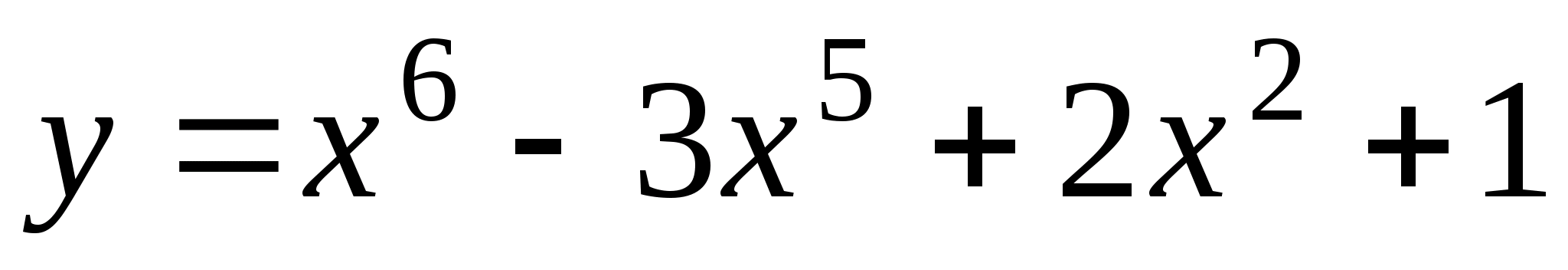 ;
;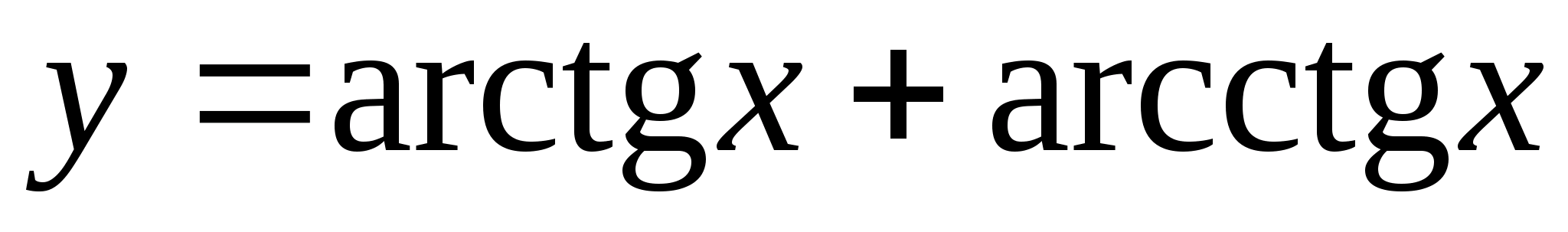 ;
; ;
; ;
; ;
; ;
; ;
; ;
;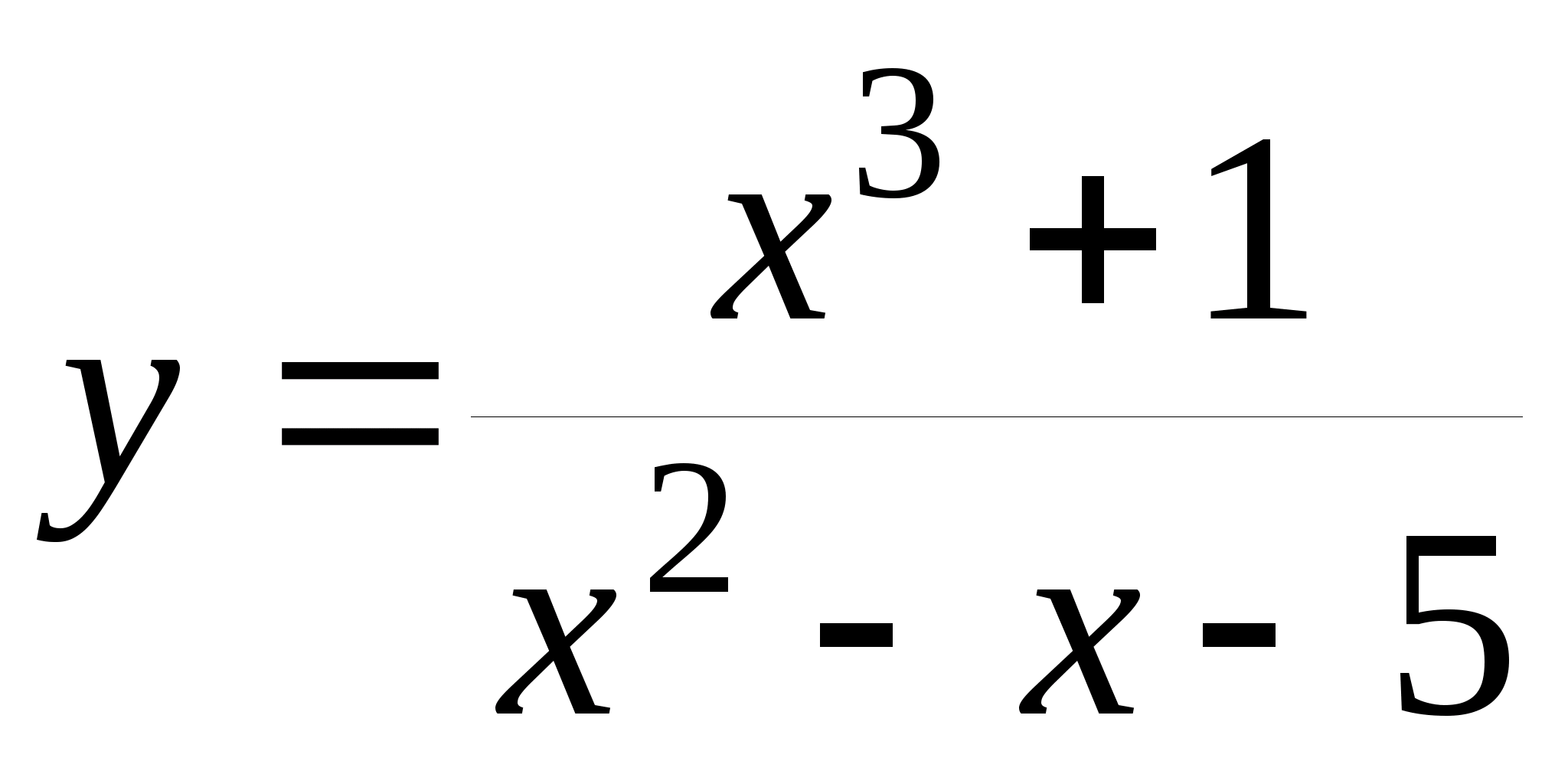 ;
;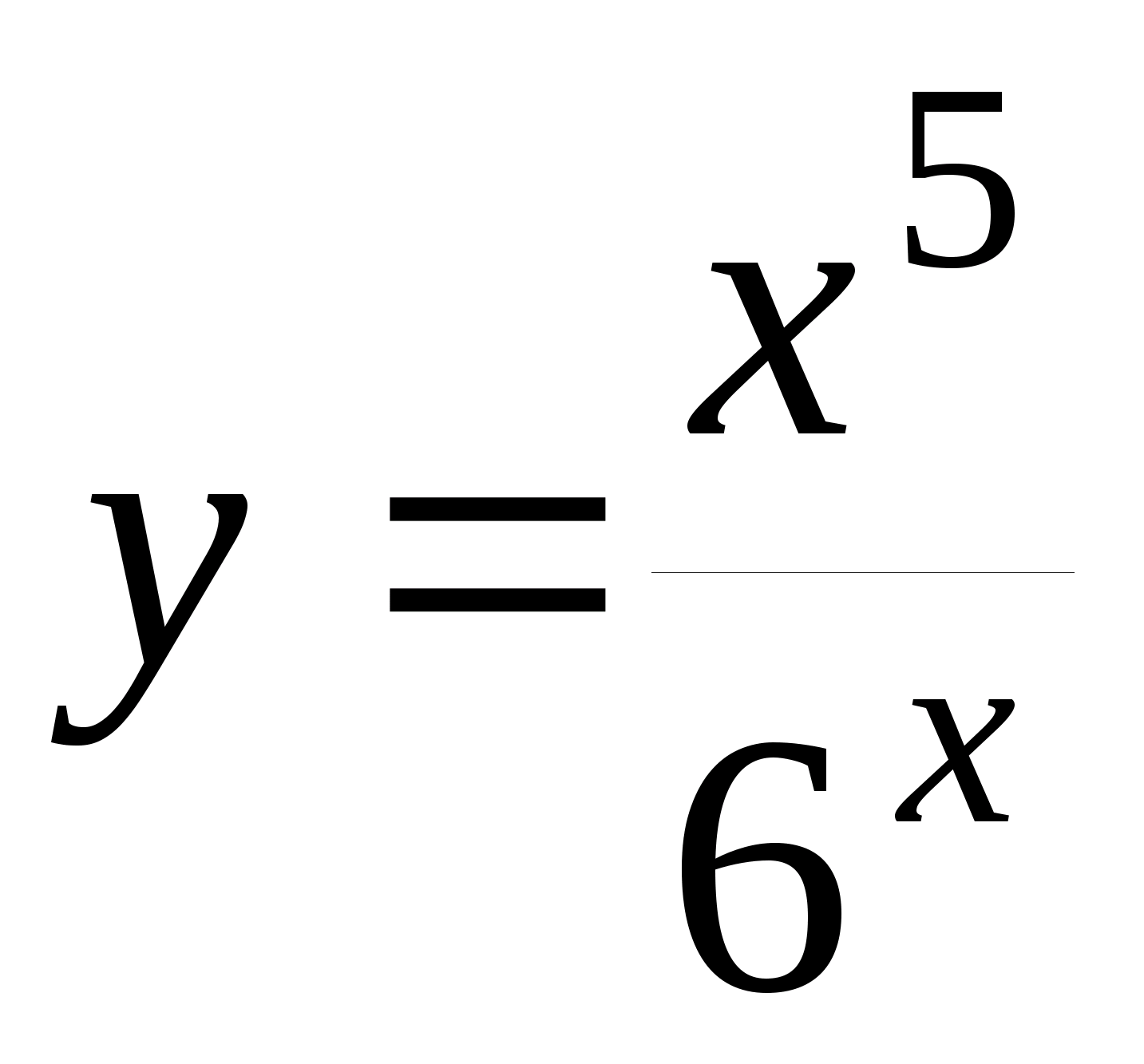 ;
; где
x = 1;
где
x = 1; ;
;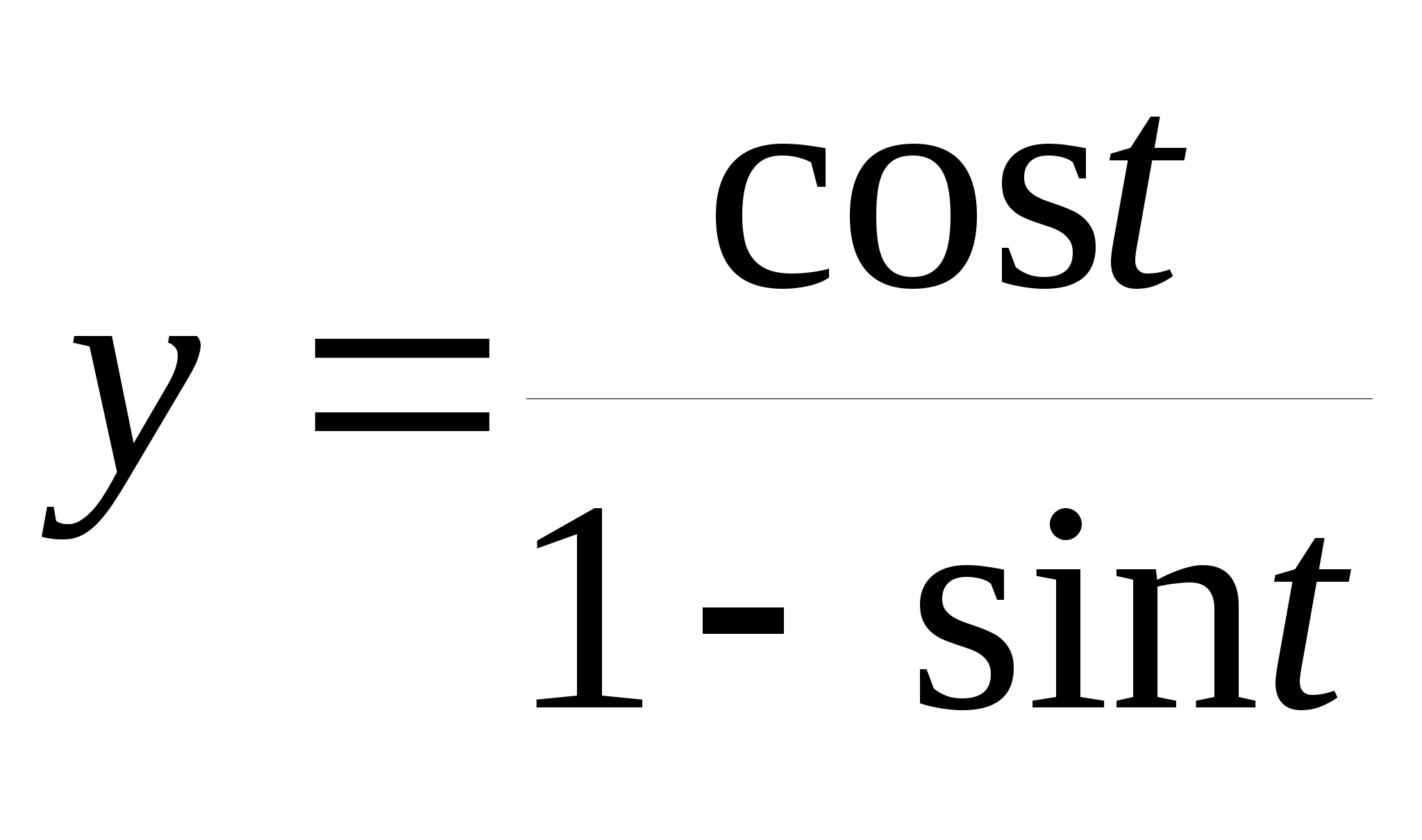 где t = / 6;
где t = / 6;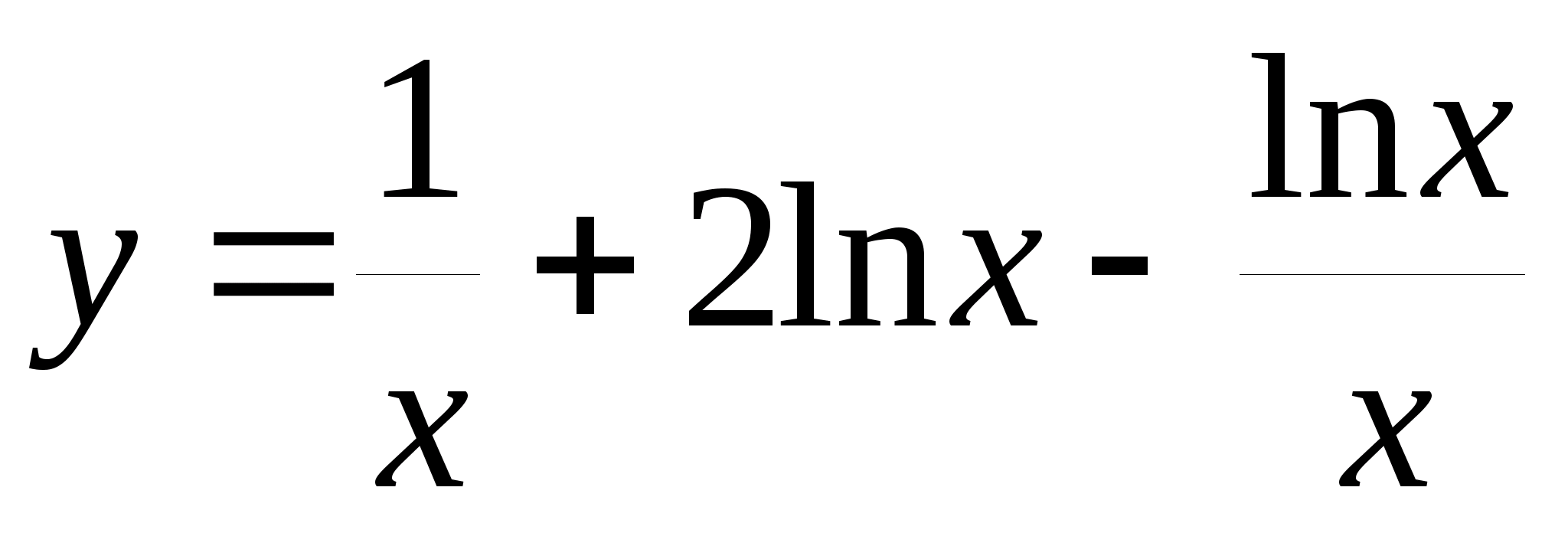
 ;
;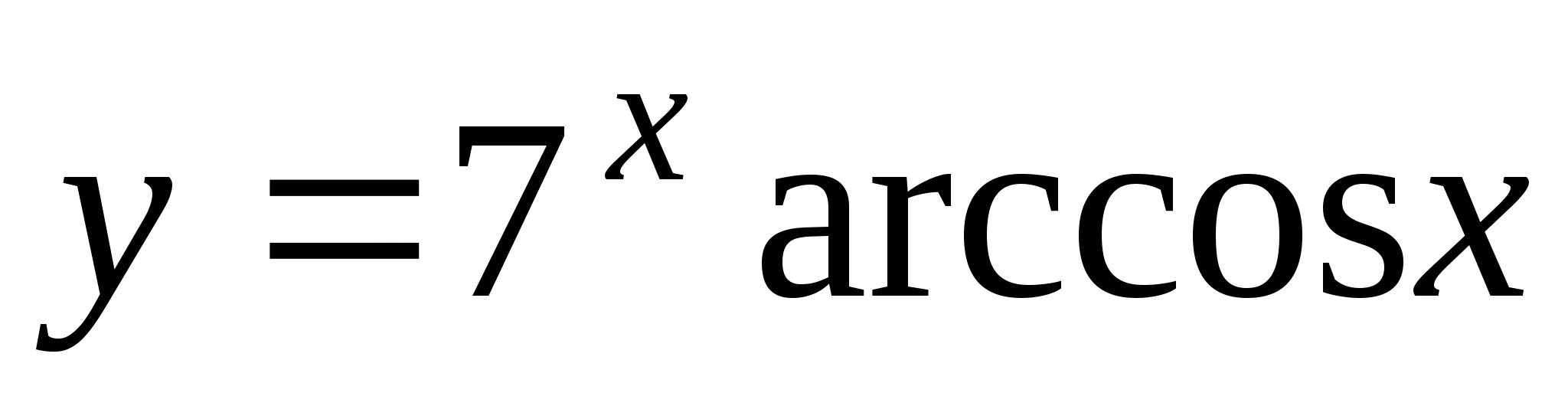 .
.