Сборник Лекций 2 по Мат.Анализу (работа 1)
Глава 3. Функция нескольких переменных
§1. Основные понятия
Пусть имеется n+1 переменная x>1>, x>2>, ..., x>n>, y, которые связаны между собой так, что каждому набору числовых значений переменных x>1>, x>2>, ..., x>n>> >соответствует единственное значение переменной y. Тогда говорят, что задана функция f от n переменных. Число y, поставленное в соответствие набору x>1>, x>2>, ..., x>n> называется значением функции f в точке (x>1>, x>2>, ..., x>n>), что записывается в виде формулы y = f(x>1>,x>2>,..., x>n>) или y =y(x>1>,x>2>,..., x>n>).
Переменные x>1>, x>2>, ..., x>n> являются аргументами этой функции, а переменная y функцией от n переменных.
Далее будем говорить лишь о функции двух переменных. Для функций большего числа переменных все факты, о которых будет идти речь, или аналогичны или сохраняются без всякого изменения. Аргументы функции двух переменных будем обозначать как правило x и y, а значение функции z.
Множество D называется областью определения функции.
Поскольку любую пару чисел x,y можно рассматривать как пару координат точки M на плоскости, вместо z=f(x,y) можно писать z=f(M).При этом аргументами функции будут координаты x,y точки M.
Числа
x,y
можно рассматривать как координаты
вектора
,
исходящего из начала координат и с
концом в точке M(x,y).
Тогда функция двух переменных будет
функцией вектора,
что записывается в виде формулы z = f(),
причем аргументами функции являются
координаты вектора .
График функции двух переменных есть множество точек (x,y,f(x,y)), где (x,y)D. График представляет собой некоторую поверхность. Пример такой
поверхности приводится на рисунке 1.
Одним из подходов к исследованию функций двух переменных является изучение поведения функции в точке, то есть определение направлений, в которых функция убывает или возрастает, и определение скорости возрастания или убывания.
Можно использовать другой подход. Пусть имеется функция z = f(x,y) c графиком, представляющим собой некоторую поверхность.
В микроэкономике, в предположении что потребитель приобретает лишь два вида товаров: A и B, вводится понятие общей полезности TU, как функции двух аргументов: Q>1> и Q>2> – количеств потребленных товаров A и B, соответственно:
TU = TU(Q>1>,Q>2>). (1)
Очевидно, что все линии уровня функции TU(Q>1>,Q>2>) составляют семейство кривых безразличия (Курс экономической теории. Под общей редакцией проф. Чепурина М.Н. 1995, стр. 125).
Пусть в плоскости XOY заданы две точки: M>0>(x>0>,y>0>) и M>1>(x>1>,y>1>). Расстояние между этими точками рассчитывается по формуле
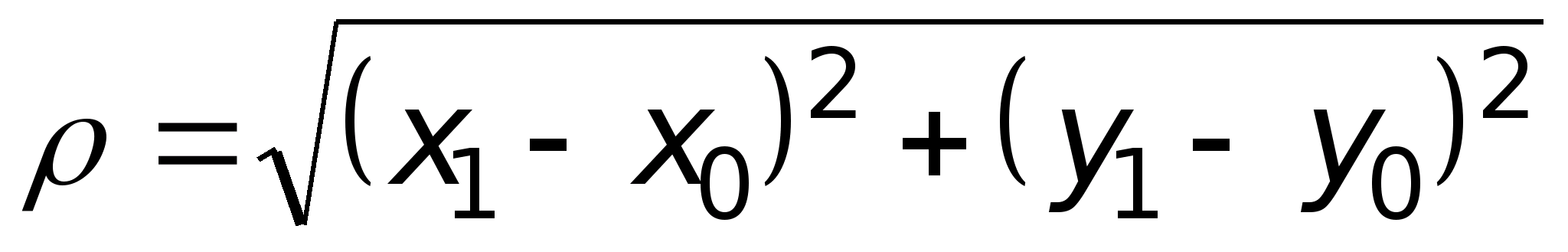. (2)
Пусть некоторое положительное число. -окрестностью V>> точки M>0>(x>0>,y>0>) называется множество всех точек, координаты x,y которых удовлетворяют неравенствам
.
Очевидно, что -окрестность точки M>0>(x>0>,y>0>) представляет собой круг радиуса с выколотым центром.
Точка M>0>(x>0>,y>0>) называется точкой минимума функции z = f(x,y), если существует такое положительное число , что из условия M(x,y) V>> (x>0>,y>0>) следует f(x,y) > f(x>0>,y>0>).
Точка M>0>(x>0>,y>0>) называется точкой максимума функции z = f(x,y), если существует такое положительное число , что из условия M(x,y) V>> (x>0>,y>0>) следует: f(x,y) < f(x>0>,y>0>).
Точки минимума и максимума называются точками экстремума.
Число A называется пределом функции z = f(x,y) в точке M>0>(x>0>,y>0>):
,
если для произвольного числа > 0 найдется такое число > 0, что для всех точек M(x,y) из -окрестности точки M>0>(x>0>,y>0>) выполняется неравенство
|f(x,y) - A|< .
Функция z = f(x,y) называется непрерывной в точке M>0>(x>0>,y>0>), если
.
Два последних определения фактически повторяют определения предела и непрерывности в точке для функции одной переменной.
§2. Частные производные
Частной производной по x функции z = f(x,y) в точке M>0>(x>0>,y>0>) называется предел
,
если этот предел существует. Обозначается эта частная производная любым из следующих символов:
;
;
.
Частная производная по x есть обычная производная от функции z = f(x,y), рассматриваемой как функция только от переменной x при фиксированном значении переменной y.
Совершенно аналогично можно определить частную производную по y функции z = f(x,y) в точке M>0>(x>0>,y>0>):
=
.
Аналогичное заключение можно сделать относительно частной производной по y.
Приведем примеры вычисления частных производных. Как говорилось выше, для вычисления частной производной по x функции z = f(x,y) нужно положить переменную y равной константе, а при нахождении частной производной по y нужно считать константой переменную x.
Примеры.
1.
.
2.
Если частные производные функции z = f(x,y) существуют на некотором множестве, а точка, в которой вычисляются частные производные несущественна, то пользуются более короткими обозначениями:
.
Сами
частные производные могут являться
функциями от нескольких переменных на
некотором множестве. У этих функций
тоже могут существовать частные
производные по x
и по y.
Они называются вторыми
частными производными
или частными производными
второго порядка и
обозначаются z>xx>, z>yy>, z>xy>
или
.
Согласно определению
;
.
Последняя частная производная второго
порядка называется смешанной. Смешанная
частная производная второго порядка,
вообще говоря, зависит от того, в какой
последовательности берутся переменные,
по которым вычисляется производная.
Так,
производная z>xy> = (z>x>
)>y>
может не быть равной z>yx> = (z>y>
)>x>.
Однако существует теорема, утверждающая,
что если смешанные
частные производные второго порядка
непрерывны, то они не зависят от того,
в какой последовательности вычислялись
частные производные по x
и по y.
(Рекомендуем читателю самому убедиться
в справедливости этой теоремы для
функций, рассмотренных в приведенных
выше примерах 1 и 2.)
Отметим очень важное отличие функции двух переменных от функции одной переменной. Из существования первых частных производных в точке не следует непрерывность функции в этой точке. Рассмотрим, например, функцию
.
График этой функции во всех точках, не принадлежащих осям координат OX и OY, представляет собой плоскость, параллельную плоскости XOY, поднятую на 1. Сами эти оси координат также принадлежат графику рассматриваемой функции. Очевидно, что в точке (0,0) функция имеет частные производные по обоим аргументам, обе равные нулю. Очевидно также, что в любой окрестности точки (0,0) можно найти точку M такую, что f(M) = 1, в то время как f(0, 0) = 0. Это означает существование разрыва функции в точке (0,0). (Пример взят из книги О.С.Ивашева-Мусатова “Начала математического анализа”).
§3. Дифференциал функции двух переменных
Рассмотрим функцию z = f(x,y), имеющую в точке Р>0>(х>0>,у>0>) частные производные f>x>(х>0>,у>0>) и f>у>(х>0>,у>0>). Перейдём от точки Р>0 >к точке R>0>(x>0>+x,y>0>+у), придавая переменным х и у в точке Р>0> произвольные приращения x и у, соответственно. При этом функция в точке Р>0> получит приращение
f(х>0>,у>0>) = f(x>0>+x,y>0>+y) – f(x>0>,y>0>) = f(R>0>) – f(P>0>).
Если приращение функции f(x,y) можно представить в виде
f(х>0>,у>0>) = f>x>(х>0>,у>0>)x + f>у>(х>0>,у>0>)у + (x;у) x + (x;у)у, (1)
где
,
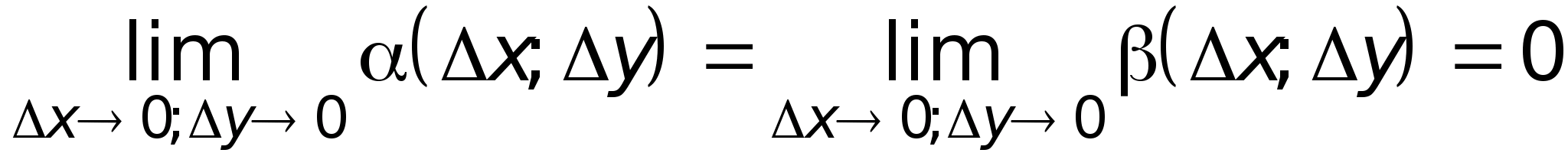то функция называется дифференцируемой
в
точке Р>0>(х>0>,у>0>).
Сумма первых двух слагаемых в правой
части равенства (1) называется дифференциалом
функции f(x,y)
в точке Р>0>
и обозначается df(x>0>,y>0>):
df(x>0>,y>0>) = f>x>(х>0>,у>0>)x + f>у>(х>0>,у>0>)у. (2)
Если точка, в которой вычисляется дифференциал не существенна, его принято обозначать просто df. Из определения следует, что дифференциал представляет собой главную часть приращения функции, линейную относительно приращений её аргументов. Полагая поочерёдно f(x,y) = х и f(x,y) = у, получим, что дифференциалы dх и dy независимых аргументов функции х и у равны соответственно x и у . Таким образом
df = f>x> dх + f>у> dу.
Раньше говорилось о том, что из существования частных производных в точке не следует непрерывности функции в этой точке. Однако, из справедливости равенства (1) следует
,
а это означает непрерывность функции в точке (х>0>,у>0>). Следовательно, дифференцируемая в точке функция обязательно непрерывна в этой точке.
Из сказанного следует, что существование обеих частных производных функции в точке не означает, что функция дифференцируема в этой точке. В курсе математического анализа доказывается теорема, что функция дифференцируема в точке, если обе частные производные этой функции непрерывны в этой точке.
На рисунке 1 график функции z = f(x,y) представляет собой поверхность F. Длина отрезка Р>0>Р равна значению функции z в точке P>0>,
то есть Р>0>Р = f(x>0>,y>0>) (на рисунке для наглядности поверхность F выбрана так, что все рассматриваемые значения функции и приращения в точке P>0> положительны, но это не ограничивает справедливости приведенных выше выводов и формул в общем случае). Координатами точек Q>0>, S>0> и R>0> являются пары чисел соответственно (x>0>,y>0>+у); (x>0>+x,y>0>) и (x>0>+x,y>0>+у), причём Q>0>Q = f(Q>0>), S>0>S = f(S>0>) и R>0>R = f(R>0>). Приращение f(х>0>,у>0>) функции в точке Р>0> равно RR>2>.
Параллелограмм PQ>1>R>1>S>1> лежит в плоскости, которая касается поверхности F в точке Р. Прямоугольник PQ>2>R>2>S>2> расположен в горизонтальной плоскости. Очевидно: Q>2>Q>1> = f>y>(x>0>,y>0>)y и S>2>S>1> = f>x>(x>0>,y>0>)x.
Из легко доказываемого равенства
R>2>R>1> = S>2>S>1> + Q>2>Q>1>
и формулы (2) следует, что дифференциал функции в точке Р>0> равен R>2>R>1>.
Так как df(x>0>,y>0>) f(x>0>,y>0>), дифференциал df даёт приближенное значение приращения функции при малых значениях приращений аргументов.
§4. Производная по направлению.
Пусть в плоскости XOY расположена точка M>0>(x>0>,y>0>). Зададим произвольный угол и рассмотрим множество точек на той же плоскости, координаты которых определяются из формул
x = x>0> + t cos, y = y>0> + t sin. (1)
Здесь t параметр, который может быть равен любому числу. Из формул (1) следует:
(y - y>0>)/(x - x>0>) = tg
Это означает, что все точки M(x,y), координаты которых удовлетворяют равенствам (1), лежат на прямой, проходящей через точку M>0>(x>0>,y>0>) и составляющей угол с осью OX. Каждому значению t соответствует единственная точка M(x,y), лежащая на этой прямой, причем согласно формуле (1) из §1 расстояние между точками M>0>(x>0>,y>0>) и M(x,y) равно t. Можно считать эту прямую числовой осью с положительным направлением, определяемым возрастанием параметра t. Обозначим положительное направление этой оси символом l.
Производной функции z = f(x,y) в точке M>0>(x>0>,y>0>) по направлению l называется число
. (2)
Производной функции по направлению можно дать геометрическую интерпретацию. Если через прямую l, определяемую формулами (1), провести вертикальную плоскость P (на самом деле в трехмерном пространстве уравнения (1) определяют эту самую плоскость), то эта плоскость пересечет поверхность-график функции z = f(x,y) вдоль
В
любом курсе математического анализа
доказывается, что производная по
направлению, определяемая формулой
(2), может быть представлена в виде
. (3)
Заметим, что частная производная по x тоже является производной по направлению. Это направление определяется равенствами: cos = 1; sin = 0. Аналогично частная производная по y — это производная по направлению, которое можно задать условиями cos = 0; sin = 1.
Прежде,
чем анализировать формулу (3), приведем
некоторые понятия и факты из курса
векторной алгебры. Пусть в плоскости с
системой координат XOY
задан направленный отрезок
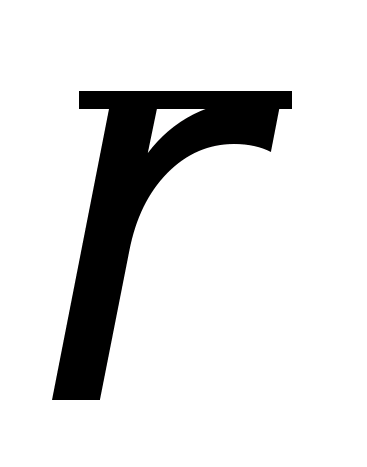или (что то же самое) вектор, причем точка
M>0>(x>0>,y>0>)
является
его начальной точкой, а M>1>(x>1>,y>1>)
конечной точкой. Определим координату
вектора по оси OX
как число, равное x>1> x>0>,
а координату по оси
,
как число, равное y>1> y>0>.
Если задать упорядоченную пару любых
чисел a
и b,
то эти числа можно рассматривать как
координаты некоторого вектора
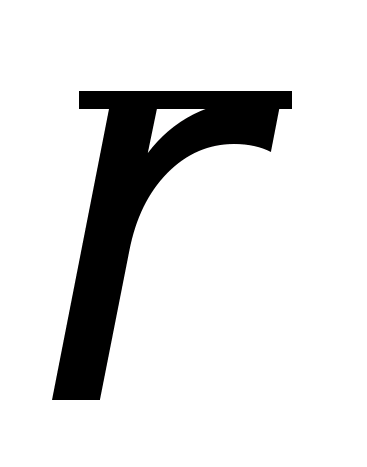в плоскости XOY,
причем длина этого вектора определена
формулой
,
а тангенс угла наклона вектора к оси OX определяется из формулы tg = b/a (отметим, что зная величину tg , а также знак любого из чисел a и b, мы можем определить угол с точностью до 2 ).
Представление
вектора в виде пары его координат будем
записывать в виде
или
.
Такое представление имеет одну характерную
особенность: оно не
определяет местоположение вектора на
плоскости
XOY.
Чтобы его определить, нужно наряду с
координатами вектора задавать, например,
координаты его начальной точки или, как
её можно назвать, точки приложения
вектора.
Если
заданы два вектора:
и
,
то скалярным
произведением
этих векторов называется число
(
угол между векторами).
В
любом курсе векторной алгебры доказывается,
что скалярное произведение векторов
и
равно сумме произведений одноименных
координат этих векторов:
= a>1>b>1> + a>2>b>2>. (4)
Пусть
в некоторой области G
плоскости XOY
задана
функция z = f(x,y),
имеющая непрерывные частные производные
по обоим аргументам. Градиентом или
вектором-градиентом
функции f(x,y)
в точке (x,y) G
называется вектор, который задается
формулой
.
Функция f определяет для каждой точки области G вектор-градиент, исходящий из этой точки.
Возвратимся теперь к формуле (3). Ее правую часть мы можем рассматривать, как скалярное произведение векторов. Первый из них вектор-градиент функции z = f(x,y) в точке M>0>(x>0>,y>0>):
.
Второй
– вектор
.
Это вектор, имеющий длину 1 и угол наклона
к оси
,
равный .
Теперь можно сделать вывод, что производная функции z = f(x,y) по направлению, определяемому углом наклона к оси OX, в точке M>0>(x>0>,y>0>) может быть вычислена по формуле
. (5)
Здесь
угол между вектором
и вектором
,
задающим направление, по которому
берется производная. Здесь также учтено,
что
.
Из формулы (5) можно сделать очень важное заключение: производная по направлению от функции z = f(x,y) в точке M>0>(x>0>,y>0>) достигает наибольшего значения, если это направление совпадает с направлением вектора-градиента функции в рассматриваемой точке, так как cos 1, и равенство достигается только если = 0 (очевидно, что другие решения уравнения cos = 1 нас в данном случае не интересуют). Иначе можно сказать, что вектор-градиент функции в точке направлен в сторону наискорейшего возрастания функции в этой точке.
Кроме того из формулы (5) следует, что наибольшее значение производной по направлению в точке или наибольшее значение скорости возрастания функции в точке равно длине вектора-градиента функции в этой точке.
Пример.
Требуется найти производную функции
по направлению, составляющему угол в
60
с осью OX,
в точке (1;3).
Найдем
частные производные функции:
Теперь можно определить градиент функции
в точке (1;3):
.
Принимая во внимание равенство
,
воспользуемся формулой (4):
.
§5. Экстремум функции двух переменных.
Точка M>0>(x>0>,y>0>) является точкой максимума (минимума) функции z = f(x,y), если найдется такая окрестность точки M>0>, что для всех точек M(x,y) из этой окрестности выполняется неравенство f(x,y)< f(x>0>,y>0>) ( f(x,y)> f(x>0>,y>0>)).
Точки максимума и минимума называются точками экстремума.
Сформулируем необходимое условие экстремума. Если в точке экстремума существует первая частная производная (по какому-либо аргументу), то она равна нулю.
Точки экстремума дифференцируемой функции (то есть функции, имеющей непрерывные частные производные во всех точках некоторой области) надо искать только среди тех точек, в которых все первые частные производные равны нулю.
Там, где выполняется необходимое условие, экстремума может и не быть (здесь полная аналогия с функцией одной переменной).
Пример:
z = xy; z>x> = y; z>y> = x; z>x>(0,0) = 0; z>y>(0,0) = 0.
Обе частные производные в точке (0,0) обращаются в 0. Однако точка (0,0) не является точкой экстремума, так как в ней самой z = 0, а в любой её окрестности есть точки, где z(x,y) > 0 (это точки, лежащие внутри первого и третьего координатных углов), и есть точки, где z(x,y) < 0 (это точки, лежащие внутри второго и четвертого координатных углов).
Для ответа на вопрос, является ли точка области определения функции точкой экстремума, нужно использовать достаточное условие экстремума. Ниже приводится его формулировка.
Пусть z>x>(x>0>,y>0>) = 0 и z>y>(x>0>,y>0>) = 0, а вторые частные производные функции z непрерывны в некоторой окрестности точки (x>0>,y>0>). Введем обозначения: A = z>xx>(x>0>,y>0>); B = z>xy>(x>0>,y>0>); C = z>yy>(x>0>,y>0>); D = AC - B2.
Тогда, если D < 0, то в точке (x>0>,y>0>) экстремума нет.
Если D > 0, то в точке (x>0>,y>0>) экстремум функции z, причем если A > 0, то минимум, а если A < 0, то максимум.
Если D = 0, то экстремум может быть, а может и не быть. В данном случае требуются дополнительные исследования.
Исследование функции двух переменных на экстремум сводится к следующему: сначала выписываются необходимые условия экстремума:
z>x>(x,y) = 0;
z>y>(x,y) = 0
которые рассматриваются как система уравнений. Ее решением является некоторое множество точек. В каждой из этих точек вычисляются значения D и проверяется выполнение достаточных условий экстремума.
§6. Метод наименьших квадратов
Пусть проводится n однородных испытаний или экспериментов, и результатом каждого испытания является пара чисел – значений некоторых переменных x и y. Испытание с номером i приводит к числам x>i>, y>i>. В качестве испытания можно, например, рассматривать выбор определенного предприятия в данной отрасли промышленности, величиной x считать объем производства продукции (например в миллионах рублей), величиной y – объем экспорта этого вида продукции (в миллионах рублей), и обследовать n предприятий отрасли.
Итогом этих испытаний является таблица:
|
|
|
|
. . . |
|
|
|
|
|
. . . |
|
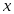рассматриваем как независимый показатель
или фактор) поставлено в соответствие
число
(величину
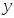рассматриваем как зависимый показатель
–
результат).
В
качестве значений
часто рассматриваются моменты времени:
t>1>, t>2>, ..., t>n>,
взятые через равные промежутки. Тогда
таблица
|
|
|
|
. . . |
|
|
|
|
|
. . . |
|
Нас интересует вопрос, как найти приближенную формулу для функции y = f(x), которая “наилучшим образом” описывала бы данные таблицы.
Пусть точки с координатами (x>i>,y>i>) группируются на плоскости вдоль некоторой прямой. Задача заключается в том, чтобы найти параметры a>0> и a>1> этой прямой:
y = a>0> + a>1>x, (1)
причем это нужно сделать так, чтобы она лучше любой другой прямой соответствовала расположению на плоскости экспериментальных точек (x>i>, y>i>).
Признаком наилучшей прямой считается минимум суммы квадратов отклонений фактических значений y, полученных из таблицы, от вычисленных по формуле (1). Эта сумма квадратов рассчитывается по формуле
S2 = (y>1> – (a>0> + a>1>x>1>))2 + (y>2> – (a>0> + a>1>x>2>))2 +...+ (y>n> – (a>0> + a>1>x>n>))2 =
.
Обратим внимание на то, что все x>i> и y>i> — известные из таблицы числа, а S2 есть функция двух переменных a>0> и a>1>.
S2 = S2(a>0>,a>1>)
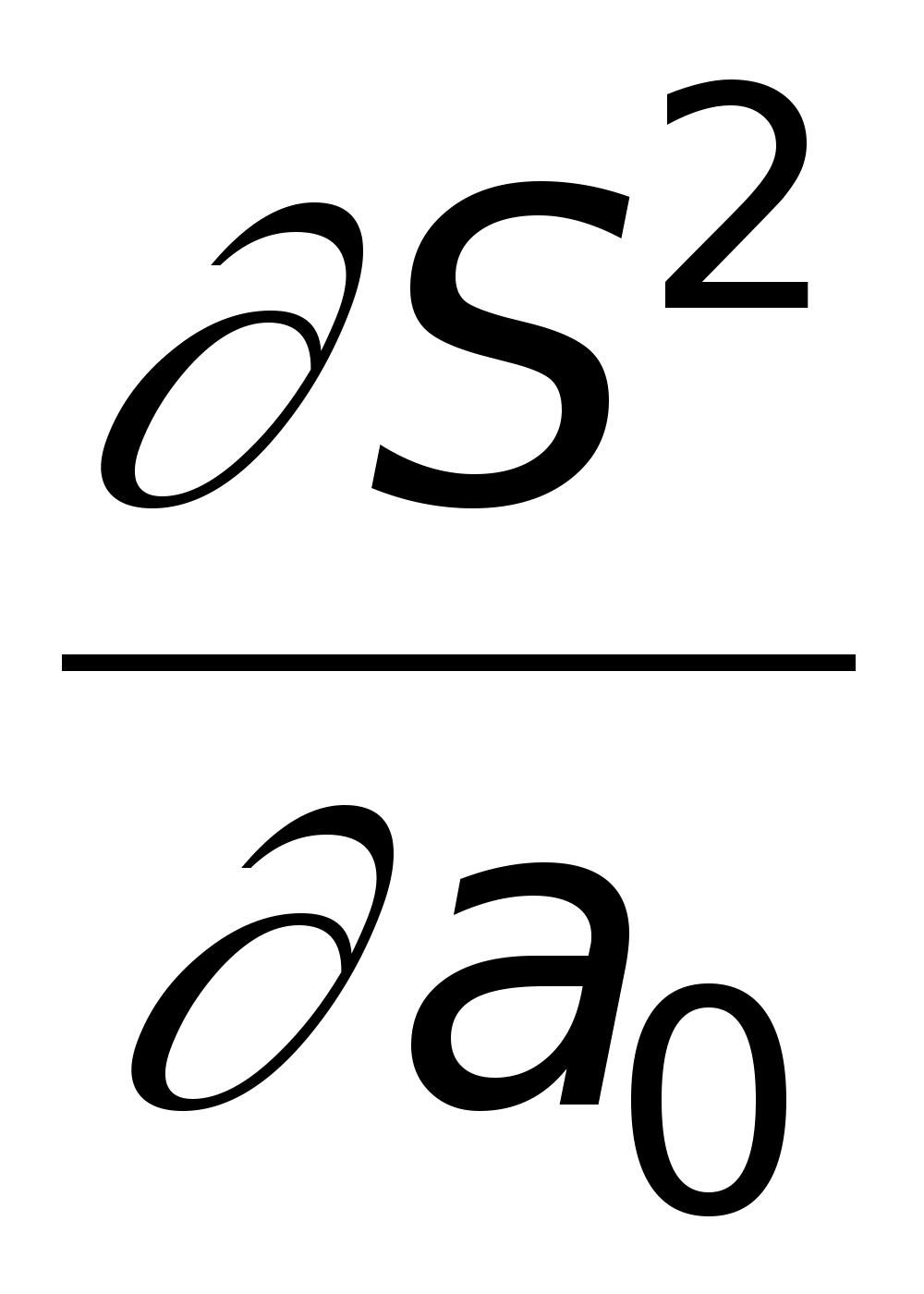и
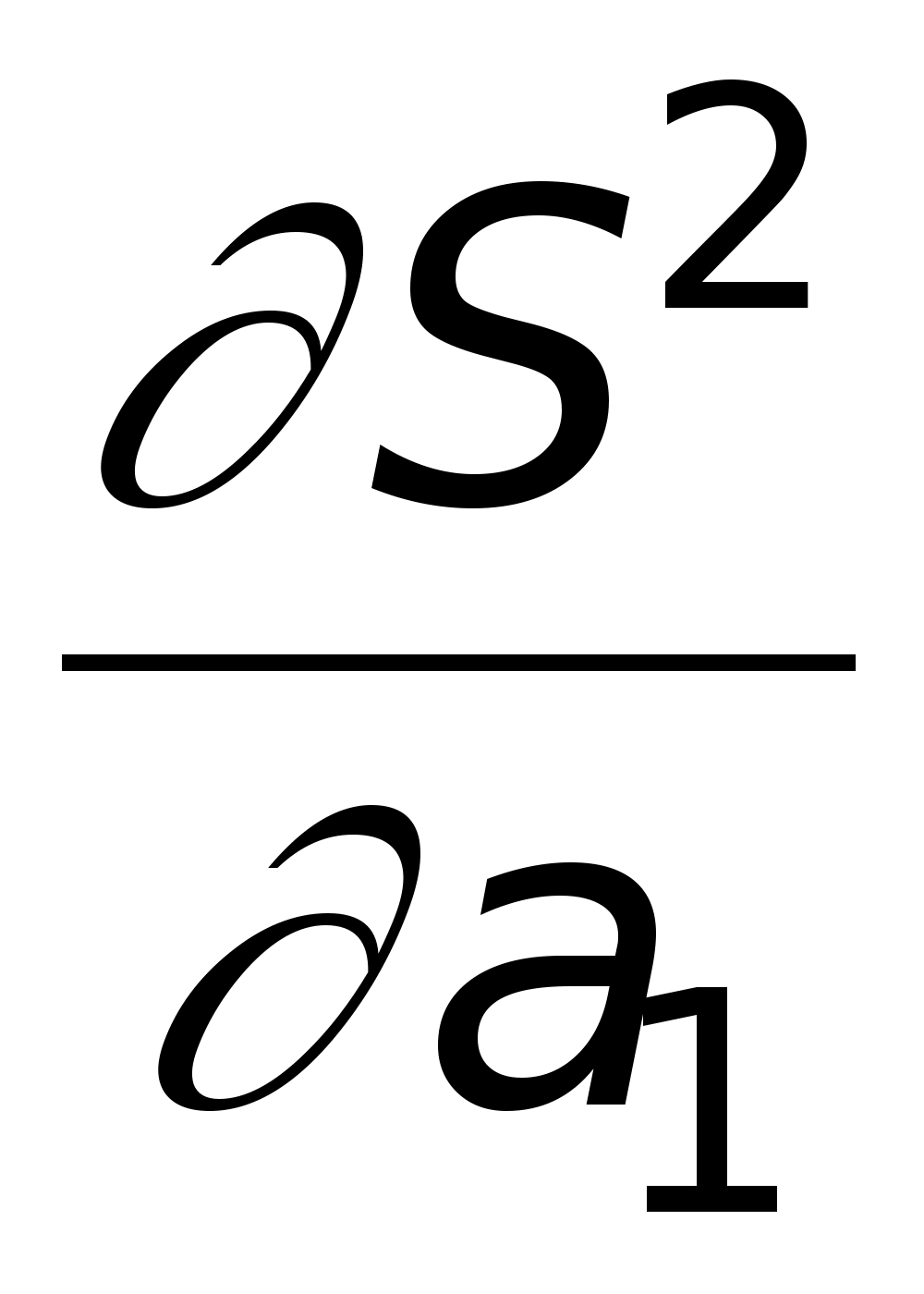равны нулю, является точкой минимума.
Отсюда следует, что точку минимума можно искать, используя лишь необходимые условия экстремума:
, (2)
. (3)
На самом деле для фунуции S2 = S2(a>0>,a>1>) достаточно легко проверить выполнение достаточных условия экстремума, тогда не нужно обращаться к графику функции. Проверку выполнения достаточных условий предоставляем читателю сделать самому.
Уравнения (2) и (3) можно преобразовать:
. (4)
Получилась так называемая система нормальных уравнений относительно неизвестных величин a>0> и a>1>.
Формула (1) с параметрами a>0>, a>1> определенными из системы (4), называется уравнением регрессии. Прямая линия, описываемая этим уравнением, называется линией регрессии. Для временных рядов обычно вместо слова “регрессия” употребляется слово тренд.
Если
экспериментальные точки в плоскости
группируются вдоль некоторой кривой
линии, то можно подобрать вместо формулы
(1) другую подходящую формулу, например,
y = a>0> + a>1>x + a>2>x2
или y = a>0 >exp(a>1>x)
с параметрами соответственно a>0>, a>1>, a>2>
и a>0>, a>1>,
подставить ее в выражение
и искать минимум получившейся функции
S2
при помощи частных производных по
параметрам.
Упражнения
1. Найти
частные производные первого порядка
от следующих функций:
|
1) |
|
2) |
|
|
3) |
|
4) |
|
|
5) |
|
6) |
|
;
;
;
;
;
;