Решение уравнений в целых числах
СОДЕРЖАНИЕ:
|
|
|
|
|
|
|
|
|
Р А З Р А Б О Т К А П Р О Г Р А М М |
|
|
|
ВВЕДЕНИЕ
Мой курсовой проект посвящен одному из наиболее интересных разделов теории чисел - решению уравнений в целых числах.
Решение в целых числах алгебраических уравнений с целыми коэффициентами более чем с одним неизвестным представляет собой одну из труднейших проблем теории чисел.
Проблема решения уравнений в целых числах решена до конца только для уравнений второй степени с двумя неизвестными. Отметим, что для уравнений любой степени с одним неизвестным она не представляет сколько-нибудь существенного интереса, так как эта задача может быть решена с помощью конечного числа проб. Для уравнений выше второй степени с двумя или более неизвестными весьма трудна не только задача нахождения всех решений в целых числах, но даже и более простая задача установления существования конечного или бесконечного множества таких решений.
В своем проекте я постаралась изложить некоторые основные результаты, полученные в теории; решения уравнений в целых числах. Теоремы, формулируемые в нем, снабжены доказательствами в тех случаях, когда эти доказательства достаточно просты.
1. УРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ
Рассмотрим уравнение первой степени с одним неизвестным
-

(1)
Пусть коэффициенты уравнения
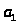 и
и
 - целые числа. Ясно, что решение этого
уравнения
- целые числа. Ясно, что решение этого
уравнения
будет целым числом только
в том случае, когда
 нацело делится на
нацело делится на
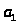 .
Таким образом, уравнение
(1) не всегда разрешимо в целых числах;
так, например, из двух уравнений
.
Таким образом, уравнение
(1) не всегда разрешимо в целых числах;
так, например, из двух уравнений
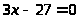 и
и
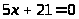 первое имеет целое решение
первое имеет целое решение
 ,
а второе в целых числах неразрешимо.
,
а второе в целых числах неразрешимо.
С тем же обстоятельством
мы встречаемся и в случае уравнений,
степень которых выше первой: квадратное
уравнение
 имеет целые решения
имеет целые решения
 ,
,
 ;
уравнение
;
уравнение
 в целых числах неразрешимо, так как его
корни
в целых числах неразрешимо, так как его
корни
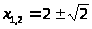 ,иррациональны.
,иррациональны.
Вопрос о нахождении целых корней уравнения n-ой степени с целыми коэффициентами
-


(2)
решается легко. Действительно,
пусть
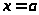 - целый корень этого уравнения. Тогда
- целый корень этого уравнения. Тогда
-
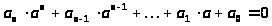 ,
, .
.
Из последнего равенства
видно, что
 делится
делится
 без остатка; следовательно, каждый целый
корень уравнения (2) является делителем
свободного члена уравнения. Для нахождения
целых решений уравнения надо выбрать
те из делителей
без остатка; следовательно, каждый целый
корень уравнения (2) является делителем
свободного члена уравнения. Для нахождения
целых решений уравнения надо выбрать
те из делителей
 ,
которые при подстановке в уравнение
обращают его в тождество. Так, например,
из чисел 1, -1, 2 и -2, представляющих собой
все делители свободного члена уравнения
,
которые при подстановке в уравнение
обращают его в тождество. Так, например,
из чисел 1, -1, 2 и -2, представляющих собой
все делители свободного члена уравнения
-
 ,
,
только -1 является корнем.
Следовательно это уравнение, имеет
единственный целый корень
 .
Тем же методом легко показать, что
уравнение
.
Тем же методом легко показать, что
уравнение
в целых числах неразрешимо.
Значительно больший интерес представляет решение в целых числах уравнении с многими неизвестными.
2. УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ДВУМЯ НЕИЗВЕСТНЫМИ
Рассмотрим уравнение первой степени с двумя неизвестными
-
 ,
,(3)
где
 и
и
 - целые числа, отличные от нуля, а
- целые числа, отличные от нуля, а
 - произвольное целое. Будем считать, что
коэффициенты
- произвольное целое. Будем считать, что
коэффициенты
 и
и
 не имеют общих делителей, кроме единицы.
Действительно, если общий наибольший
делитель этих коэффициентов
не имеют общих делителей, кроме единицы.
Действительно, если общий наибольший
делитель этих коэффициентов
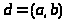 отличен от единицы, то справедливы
равенства
отличен от единицы, то справедливы
равенства
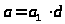 ,
,
 ;
уравнение (3) принимает вид
;
уравнение (3) принимает вид
и может иметь целые решения
только в том случае, когда
 делится на
делится на
 .
Таким образом, в случае
.
Таким образом, в случае
 - все коэффициенты уравнения (3) должны
делиться нацело на
- все коэффициенты уравнения (3) должны
делиться нацело на
 ,
и, сокращая (3) на
,
и, сокращая (3) на
 ,
придем к уравнению
,
придем к уравнению
-
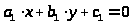
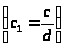 ,
,
коэффициенты которого
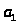 и
и
 взаимно просты.
взаимно просты.
Рассмотрим сначала случай,
когда
 .
Уравнение (3) перепишется так:
.
Уравнение (3) перепишется так:
-
 .
.(3')
Решая это уравнение
относительно ,
получим
,
получим
-
 .
.
Ясно, что
 будет принимать целые значения в том и
только в том случае, когда
будет принимать целые значения в том и
только в том случае, когда
 делится на
делится на
 без остатка. Но всякое целое
без остатка. Но всякое целое
 ,
кратное
,
кратное
 ,
можно записать в виде
,
можно записать в виде
-
 ,
,
где
 принимает произвольные целые значения
принимает произвольные целые значения
 .
Подставим это значение
.
Подставим это значение
 в предыдущее уравнение,
тогда
в предыдущее уравнение,
тогда
-
 ,
,
и мы получаем формулы, содержащие все целые решения уравнения (3'):
-
 ,
,

 .
.
Перейдем теперь к случаю
 .
.
Покажем, прежде всего, что
для нахождения всех целых решений
уравнения (3) достаточно найти какое-нибудь
одно его решение, т. е. найти такие целые
числа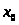 ,
,
 ,
для которых
,
для которых
-
 ,
,
Т е о р е м а I.
Пусть а и b
взаимно просты и
 -
какое-нибудь решение уравнения
-
какое-нибудь решение уравнения
-
 ,
,(3)
Тогда формулы
-
 ,
,
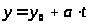
(4)
при
 дают все решения уравнения (3).
дают все решения уравнения (3).
Д о к а з а т е л ь с т в о.
Пусть
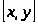 - произвольное решение уравнения (3).
Тогда из равенств
- произвольное решение уравнения (3).
Тогда из равенств
-
 и
и

получаем
-
 ;
;
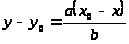 .
.
Так как
 -
целое число и числа
-
целое число и числа
 и
и
 взаимно просты, то
взаимно просты, то
 должно нацело делиться на
должно нацело делиться на
 ,
т. е.
,
т. е.
 имеет вид
имеет вид
-
 ,
,
где
 - целое. Но тогда
- целое. Но тогда
-
 ,
,
и получаем
-
 ,
,
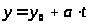 .
.
Таким образом доказано, что
всякое решение
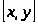 имеет вид (4). Остается еще проверить,
что всякая пара чисел
имеет вид (4). Остается еще проверить,
что всякая пара чисел
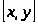 ,
получаемая по формулам
(4) при целом
,
получаемая по формулам
(4) при целом
 ,
будет решением
уравнения (3).
Чтобы провести та кую
проверку, подставим величины
,
будет решением
уравнения (3).
Чтобы провести та кую
проверку, подставим величины
 ,
,
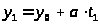 в левую часть уравнения (3):
в левую часть уравнения (3):
-
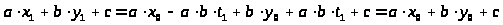 ,
,
но так как
 -решение,
то
-решение,
то
 и, следовательно,
и, следовательно,
 ,
т.е.
,
т.е.
 - решение уравнения (3), чем теорема
полностью доказана.
- решение уравнения (3), чем теорема
полностью доказана.
Итак, если известно одно
решение уравнения
 ,
то все остальные решения найдутся из
арифметических прогрессий, общие члены
которых имеют вид:
,
то все остальные решения найдутся из
арифметических прогрессий, общие члены
которых имеют вид:
 ,
,
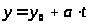
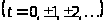 .
.
3аметим, что в случае, когда
 ,
найденные раньше формулы решений
,
найденные раньше формулы решений
-
 ,
,

могут быть получены из
только что выведенных формул
 ,
,
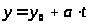 ,
если выбрать
,
если выбрать
 ,
что можно сделать, так как значения
,
что можно сделать, так как значения
 ,
,
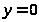 являются, очевидно, решением уравнения
являются, очевидно, решением уравнения
-
 ,
,
Как же найти какое-нибудь
одно решение
 уравнения (3) в общем случае, когда
уравнения (3) в общем случае, когда
 .
Начнем с примера.
.
Начнем с примера.
Пусть дано уравнение
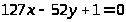
Преобразуем отношение коэффициентов при неизвестных.
Прежде всего, выделим целую
часть неправильной дроби
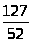 ;
;

Правильную дробь
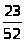 заменим равной ей дробью
заменим равной ей дробью
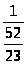 .
.
Тогда получим
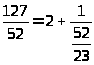 .
Проделаем такие же
преобразования с полученной в знаменателе
неправильной дробью
.
Проделаем такие же
преобразования с полученной в знаменателе
неправильной дробью
 .
.
Теперь исходная дробь примет
вид:

Повторяя те же рассуждения
для дроби
 получим
получим
 .
.
Выделяя целую часть
неправильной дроби ,
придем к окончательному результату:
,
придем к окончательному результату:
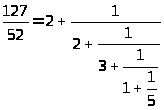
Мы получили выражение,
которое называется конечной
цепной или непрерывной
дробью. Отбросив
последнее звено этой
цепной дроби - одну пятую, превратим
получающуюся при этом новую цепную
дробь в простую и вычтем ее из исходной
дроби
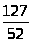 :
:
 ,
,
 .
.
Приведем полученное выражение к общему знаменателю и отбросим его, тогда
 .
.
Из сопоставления полученного
равенства с уравнением
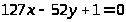 следует, что
следует, что
 ,
,
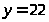 будет решением этого уравнения и согласно
теореме все его решения будут содержаться
в прогрессиях
будет решением этого уравнения и согласно
теореме все его решения будут содержаться
в прогрессиях
 ,
,

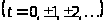 .
.
Полученный результат наводит
на мысль о том, что и в общем случае для
нахождения решения уравнения
 надо разложить отношение коэффициентов
при неизвестных в цепкую дробь, отбросить
ее последнее звено и проделать выкладки,
подобные тем, которые были проведены
выше.
надо разложить отношение коэффициентов
при неизвестных в цепкую дробь, отбросить
ее последнее звено и проделать выкладки,
подобные тем, которые были проведены
выше.
Для доказательства этого предположения будут нужны некоторые свойства цепных дробей.
Рассмотрим несократимую
дробь
 .
Обозначим через
.
Обозначим через
 частное и через
частное и через
 остаток от деления а
на b.
Тогда получим:
остаток от деления а
на b.
Тогда получим:
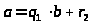 ,
,
 .
.
Пусть, далее,
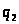 -
частное и
-
частное и
 - остаток от деления
- остаток от деления
 на
на
 Тогда
Тогда
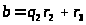 ,
,
 ;
точно так же
;
точно так же
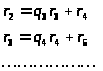


Величины
 ,
,
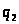 ,…
называются неполными
частными.
Приведенный выше процесс
образования неполных частных называется
алгоритмом Евклида.
Остатки от деления
,…
называются неполными
частными.
Приведенный выше процесс
образования неполных частных называется
алгоритмом Евклида.
Остатки от деления
 ,
,
 ,…удовлетворяют
неравенствам
,…удовлетворяют
неравенствам
-
 ,
,(5)
т. е. образуют ряд убывающих неотрицательных чисел.
Так как количество
неотрицательных целых чисел, не
превосходящих b,
не может быть
бесконечным, то на некотором шаге процесс
образования неполных частных оборвется
из-за обращения в ноль очередного остатка
r.
Пусть
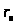 - последний отличный от нуля остаток в
ряде (5); тогда
- последний отличный от нуля остаток в
ряде (5); тогда
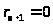 и алгоритм Евклида для чисел a
и b
примет вид
и алгоритм Евклида для чисел a
и b
примет вид
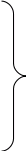
 (6)
(6)
Перепишем полученные равенства в виде

Заменяя значение
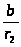 в первой строке этих равенств
соответствующим значением из второй
строки значение
в первой строке этих равенств
соответствующим значением из второй
строки значение
 - выражением из третьей, строки и т. д.,
получим разложение
- выражением из третьей, строки и т. д.,
получим разложение
 в цепную дробь:
в цепную дробь:



Выражения, получающиеся из
цепной дроби при отбрасывании всех ее
звеньев, начиная с некоторого звена,
назовем подходящими
дробями. Первая:
подходящая дробь
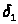 получится при отбрасывании всех звеньев,
начиная с
получится при отбрасывании всех звеньев,
начиная с
 :
:
 .
.
Вторая подходящая дробь
 получается
отбрасыванием всех звеньев, начиная с
получается
отбрасыванием всех звеньев, начиная с
 :
:
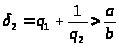 .
Точно так же
.
Точно так же

и т. д.
В силу способа образования подходящих дробей возникают очевидные неравенства:
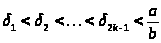 ;
;
 .
.
Запишем k-ю
подходящую дробь
 в виде
в виде

 ,
,
и найдем закон образования
числителей и знаменателей подходящих
дробей, Преобразуем первые подходящие
дроби
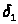 ,
,
 ,
,
 :
:
 ;
;
 ,
,
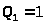 ;
;
 ;
;
 ;
;
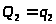 ;
;
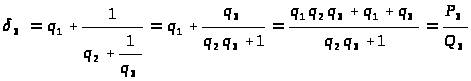 ;
;
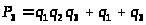 ;
;
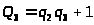
Отсюда получаем:
 ;
;
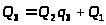 .
.
Применяя индукцию, докажем, что соотношения того же вида
 ,
,
 (7).
(7).
выполняются для всех
 .
.
Действительно, пусть
равенства (7) выполняются для некоторого
 .
Из определения подходящих дробей
непосредственно следует, что при замене
в выражении
.
Из определения подходящих дробей
непосредственно следует, что при замене
в выражении
 величины
величины
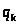 на
на
 перейдет в
перейдет в
 .
Согласно индукционному предположению
.
Согласно индукционному предположению
 .
.
Заменяя здесь
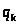 на
на
 ,
получим:
,
получим:
 .
.
Отсюда, так как
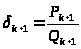 ,
следует, что
,
следует, что
 ,
,
 .
.
Таким образом, из выполнения
равенств (7) для некоторого
 следует выполнение их для
следует выполнение их для
 Но для
Но для
 равенства (7) - выполняется и, следовательно,
их справедливость установлена для всех
равенства (7) - выполняется и, следовательно,
их справедливость установлена для всех
 .
.
Покажем теперь, что разность
соседних подходящих дробей
 удовлетворяет соотношению
удовлетворяет соотношению

 .
(8)
.
(8)
Действительно,
 .
.
Пользуясь формулами (7), преобразуем числитель полученной дроби:
 .
.
Выражение, стоящее в скобках,
получается из исходного заменой
 на
на
 .
Повторяя такие же преобразования для
получающихся выражений, получим,
очевидно, цепь равенств:
.
Повторяя такие же преобразования для
получающихся выражений, получим,
очевидно, цепь равенств:



Отсюда следует, что
Если разложение
 в цепную дробь имеет
в цепную дробь имеет
 звеньев, то п-я подходящая
дробь
звеньев, то п-я подходящая
дробь
 совпадает с
совпадает с
 .
Применяя равенство (8), при
.
Применяя равенство (8), при
 получим
получим
 (9)
(9)
Вернемся теперь к решению уравнения
 ,
,
 (10)
(10)
Перепишем соотношение (9) в
виде
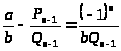 .
.
Приводя к общему знаменателю и отбрасывая его, получим

Умножим это соотношение на
 .
Тогда
.
Тогда

Отсюда следует, что пара
чисел
 ,
,
 ,
,
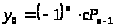 ,
(11)
,
(11)
является решением уравнения (10) и согласно теореме все решения этого уравнения имеют вид
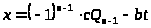 ,
,


Полученный результат полностью решает вопрос о нахождении всех целочисленных решений уравнения первой степени с двумя неизвестными. Перейдем теперь к рассмотрению некоторых уравнений второй степени.
3. ПРИМЕРЫ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ С ТРЕМЯ НЕИЗВЕСТНЫМИ
П р и м е р I. Рассмотрим уравнение второй степени с тремя неизвестными:
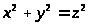 (12)
(12)
Геометрически решение этого
уравнения в целых числах можно истолковать
как нахождение всех пифагоровых
треугольников, т. е. прямоугольных
треугольников, у которых и катеты
 ,
,
 и
гипотенуза
и
гипотенуза
 выражаются целыми числами.
выражаются целыми числами.
Обозначим через
 общий наибольший делитель чисел
общий наибольший делитель чисел
 и
и
 :
:
 .
Тогда
.
Тогда
 ,
,
 ,
,
и уравнение (12) примет вид
 .
.
Отсюда следует, что
 делится на
делится на
 и, значит,
и, значит,
 кратно
кратно
 :
:
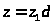 .
.
Теперь уравнение (12) можно записать в виде
 ;
;
сокращая на
 ,
получим
,
получим
 .
.
Мы пришли к уравнению того
же вида, что и исходное, причем теперь
величины
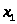 и
и
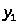 не имеют общих делителей, кроме 1. Таким
образом, при решении уравнения (12) можно
ограничиться случаем, когда
не имеют общих делителей, кроме 1. Таким
образом, при решении уравнения (12) можно
ограничиться случаем, когда
 и
и
 взаимно просты. Итак, пусть
взаимно просты. Итак, пусть
 .
Тогда хотя бы одна из величин
.
Тогда хотя бы одна из величин
 и
и
 (например,
(например,
 )
будет нечетной.
Перенося
)
будет нечетной.
Перенося
 в правую часть уравнения (12), получим
в правую часть уравнения (12), получим
 ;
;
 .
(13)
.
(13)
Обозначим через
 общий наибольший делитель выражений
общий наибольший делитель выражений
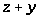 и
и
 .
Тогда
.
Тогда
 ,
,
 ,
(14)
,
(14)
где
 и
и
 взаимно просты.
взаимно просты.
Подставляя в (13) значения
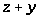 и
и
 ,
получим
,
получим
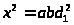 .
.
Так как числа
 и
и
 не имеют общих делителей, то полученное
равенство возможно только в том случае,
когда
не имеют общих делителей, то полученное
равенство возможно только в том случае,
когда
 и
и
 будут полными квадратами:
будут полными квадратами:
 ,
,
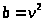 .
.
Но тогда

и
 (15)
(15)
Найдем теперь
 и
и
 из равенств (14). Сложение этих равенств
дает:
из равенств (14). Сложение этих равенств
дает:
 ;
;
 .
(16)
.
(16)
Вычитая второе из равенств (14) из первого, получим
 ;
;
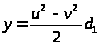 (17)
(17)
В силу нечетности
 из (15) получаем, что
из (15) получаем, что
 ,
,
 и
и
 также нечетны. Более того,
также нечетны. Более того,
 ,
так как иначе из равенств
,
так как иначе из равенств
 и
и
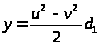
следовало бы, что величины
 и
и
 имеют общий делитель
имеют общий делитель
 ,
что противоречит предположению об их
взаимной простоте. Числа
,
что противоречит предположению об их
взаимной простоте. Числа
 и
и
 связаны с взаимно простыми числами
связаны с взаимно простыми числами
 и
и
 равенствами
равенствами
 ,
,
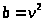
и в силу этого сами взаимно
просты;
 ,
так как
,
так как
 ,
что ясно из равенств (14).
,
что ясно из равенств (14).
Подставляя в равенства (15)
- (17)
 ,
получим формулы:
,
получим формулы:
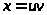 ,
,
 ,
,
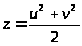 ,
(18)
,
(18)
дающие при нечетных взаимно
простых
 и
и

 все свободные
от общих делителей тройки целых
положительных чисел
все свободные
от общих делителей тройки целых
положительных чисел
 ,
,
 ,
,
 ,
удовлетворяющие уравнению (12).
Простой подстановкой
,
удовлетворяющие уравнению (12).
Простой подстановкой
 ,
,
 и
и
 в уравнение (12) легко проверить, что при
любых
в уравнение (12) легко проверить, что при
любых
 и
и
 числа (18) удовлетворяют этому уравнению.
числа (18) удовлетворяют этому уравнению.
Для начальных значений
 и
и
 формулы (18) приводят к следующим часто
встречающимся равенствам:
формулы (18) приводят к следующим часто
встречающимся равенствам:
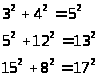


Как уже было сказано, формулы (18) дают только те решения уравнения
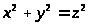 ,
,
в которых числа
 ,
,
 и
и
 не имеют общих делителей. Все остальные
целые положительные решения-этого
уравнения получаются умножением решений,
содержащихся в формулах (18), на произвольный
общий множитель
не имеют общих делителей. Все остальные
целые положительные решения-этого
уравнения получаются умножением решений,
содержащихся в формулах (18), на произвольный
общий множитель
 .
.
Тем же путем, каким мы получили все решения уравнения (12), могут быть получены и все решения других уравнений того же типа.
П р и м е р II. Найдем все решения уравнения
 (19)
(19)
в целых положительных
попарно взаимно простых числах
 ,
,
 ,
,
 .
.
Заметим, что если
 ,
,
 ,
,
 есть решение уравнения (19) и
есть решение уравнения (19) и
 ,
,
 ,
,
 не имеют общего делителя, отличного от
1, то они и попарно взаимно просты.
Действительно, если
не имеют общего делителя, отличного от
1, то они и попарно взаимно просты.
Действительно, если
 и
и
 кратны простому числу
кратны простому числу
 ,
то из равенства
,
то из равенства

следует, так как его левая
часть - целое число, что
 кратно
кратно
 .
То же самое будет,
если
.
То же самое будет,
если
 и
и
 или
или
 и
и
 делятся на
делятся на
 .
.
Заметим, что
 должно быть числом нечетным для того,
чтобы общий наибольший делитель
должно быть числом нечетным для того,
чтобы общий наибольший делитель
 ,
,
 ,
,
 был равен 1. Действительно, если
был равен 1. Действительно, если
 четно, то левая часть уравнения (19) будет
четным числом и, значит, z
также будет четным. Но
четно, то левая часть уравнения (19) будет
четным числом и, значит, z
также будет четным. Но
 и
и
 будут тогда кратны 4. Отсюда следует,
что
будут тогда кратны 4. Отсюда следует,
что
 должно делиться на 4, другими словами,
что
должно делиться на 4, другими словами,
что
 тоже должно быть четным числом. Значит,
если
тоже должно быть четным числом. Значит,
если
 четно, то все числа
четно, то все числа
 ,
,
 ,
,
 должны быть четными. Итак, в решении без
общего отличного от 1 делителя
должны быть четными. Итак, в решении без
общего отличного от 1 делителя
 должно быть нечетным. Отсюда уже следует,
что и
должно быть нечетным. Отсюда уже следует,
что и
 должно быть тоже нечетным. Перенося
должно быть тоже нечетным. Перенося
 в правую часть, мы получаем:
в правую часть, мы получаем:
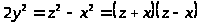 .
.
Но
 и
и
 имеют общим наибольшим делителем 2.
Действительно, пусть их общий наибольший
делитель будет
имеют общим наибольшим делителем 2.
Действительно, пусть их общий наибольший
делитель будет
 .
Тогда
.
Тогда
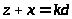 ,
,
 ,
,
где
 и
и
 - целые числа. Складывая и вычитая эти
равенства, мы будем иметь:
- целые числа. Складывая и вычитая эти
равенства, мы будем иметь:
 ,
, .
.
Но
 и
и
 нечетны и взаимно просты. Поэтому общий
наибольший делитель
нечетны и взаимно просты. Поэтому общий
наибольший делитель
 и
и
 будет 2. Отсюда следует, что
будет 2. Отсюда следует, что
 .
.
Итак, или
 ,
или
,
или
 нечетно. Поэтому или
нечетно. Поэтому или
числа
 и
и

взаимно просты, или взаимно просты числа
 и
и
 .
.
В первом случае из равенства

следует, что
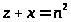 ,
,
 ,
,
а во втором случае из равенства

следует
 ,
,
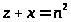 ,
,
где
 и
и
 целые,
целые,
 - нечетное число и
- нечетное число и
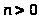 ,
,
 .
Решая эти две системы уравнений
относительно
.
Решая эти две системы уравнений
относительно
 и
и
 и находя
и находя
 ,
мы получаем или
,
мы получаем или
 ,
,
 ,
,
 или
или
 ,
,
 ,
,
 ,
,
где
 нечетно. Объединяя эти две формы
представления решения
нечетно. Объединяя эти две формы
представления решения
 ,
,
 ,
,
 мы получаем общую формулу
мы получаем общую формулу
 ,
,
 ,
,
 ,
,
где
 нечетно. Но для того чтобы
нечетно. Но для того чтобы
 и
и
 были целыми числами, необходимо, чтобы
были целыми числами, необходимо, чтобы
 было четным. Полагая
было четным. Полагая
 и
и
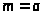 ,
мы получим окончательно общие
формулы, дающие все решения уравнения
(19) в
целых положительных без общего делителя,
большего 1, числах
,
мы получим окончательно общие
формулы, дающие все решения уравнения
(19) в
целых положительных без общего делителя,
большего 1, числах ,
,
 ,
,
 :
:
 ,
,
 ,
,
 ,
(19')
,
(19')
где
 и
и
 положительны, взаимно просты и
положительны, взаимно просты и
 нечетно. При этих
условиях величины
нечетно. При этих
условиях величины
 и
и
 выбираются произвольно,
но так, чтобы
выбираются произвольно,
но так, чтобы
 было положительно.
Формулы (19') действительно дают все
решения в целых положительных и взаимно
простых числах
было положительно.
Формулы (19') действительно дают все
решения в целых положительных и взаимно
простых числах
 ,
,
 ,
,
 ,
так как, с одной
стороны, мы доказали, что
,
так как, с одной
стороны, мы доказали, что
 ,
,
 ,
,
 в этом случае должны представляться по
формулам (19'), а с другой стороны, если
мы зададим числа
в этом случае должны представляться по
формулам (19'), а с другой стороны, если
мы зададим числа
 и
и
 ,
удовлетворяющие нашим
условиям, то
,
удовлетворяющие нашим
условиям, то
 ,
,
 ,
,
 будут действительно взаимно просты и
будут решением уравнения (19).
будут действительно взаимно просты и
будут решением уравнения (19).
4. ОБЩИЙ СЛУЧАЙ УРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ С ДВУМЯ НЕИЗВЕСТНЫМИ
В этом пункте мы докажем,
что при любом целом положительном
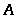 и иррациональном
и иррациональном
 уравнение
уравнение
 (20)
(20)
всегда имеет нетривиальное
решение, другими словами существует
пара целых чисел
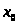 и
и
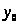 ;
;
 ,
которая ему удовлетворяет. Прежде всего,
укажем прием, позволяющий разложить в
цепную дробь произвольное положительное
число. Пусть
,
которая ему удовлетворяет. Прежде всего,
укажем прием, позволяющий разложить в
цепную дробь произвольное положительное
число. Пусть
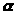 - любое положительное число. Тогда всегда
существует целое число, которое будет
меньше или равно
- любое положительное число. Тогда всегда
существует целое число, которое будет
меньше или равно
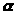 и больше
и больше
 .
Такое целое число носит название целой
части
.
Такое целое число носит название целой
части
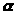 и обозначается
и обозначается
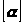 .
Разность между
.
Разность между
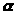 и его целой частью называется дробной
частью числа
и его целой частью называется дробной
частью числа
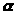 и обозначается
и обозначается
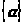 .
Из определений целой части и дробной
части числа
.
Из определений целой части и дробной
части числа
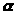 непосредственно следует соотношение
между ними, именно:
непосредственно следует соотношение
между ними, именно:
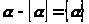
или
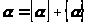 .
(21)
.
(21)
Так как дробная часть числа
есть разность между положительным
числом и наибольшим целым числом, его
не превосходящим, то дробная часть числа
всегда меньше единицы и неотрицательна.
Например, целая часть
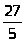 есть 5, а дробная его часть есть
есть 5, а дробная его часть есть
 ,
целая часть
,
целая часть
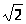 есть 1, а дробная часть равна
есть 1, а дробная часть равна
 ;
целая часть
;
целая часть
 равна 3, а дробная часть равна
равна 3, а дробная часть равна
 ,
и т. д.
,
и т. д.
Введенное нами определение
целой части и дробной части положительного
числа
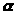 может быть использовано для разложения
этого числа в цепную дробь. Положим:
может быть использовано для разложения
этого числа в цепную дробь. Положим:
 ,
,
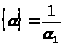 .
.
Тогда
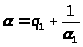 .
.
Так как
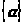 всегда меньше единицы, то
всегда меньше единицы, то
 всегда больше единицы. Если бы
всегда больше единицы. Если бы
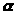 было само целым числом, то его дробная
часть равнялась бы нулю,
было само целым числом, то его дробная
часть равнялась бы нулю,
 было бы равно бесконечности и мы имели
бы равенство
было бы равно бесконечности и мы имели
бы равенство
 .
Отвлекаясь от этого
частного случая, который исключается
тем, что мы разлагаем в непрерывную
дробь иррациональное число, мы можем
утверждать, что
.
Отвлекаясь от этого
частного случая, который исключается
тем, что мы разлагаем в непрерывную
дробь иррациональное число, мы можем
утверждать, что
 - положительное число, большее единицы.
С этим числом
- положительное число, большее единицы.
С этим числом
 мы поступаем так же, как и с
мы поступаем так же, как и с
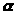 ,
и пишем равенство
,
и пишем равенство
 ,
,
 ,
,

Продолжая этот процесс, мы получаем ряд равенств:

 (24)
(24)
Этот процесс последовательного
образования целых чисел
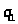 ,
,
 ,
,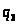 ,
, ,
, ,
, в случае, когда
в случае, когда
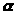 ,
- рациональное число,
- другими словами, когда
,
- рациональное число,
- другими словами, когда
 ,
где
,
где
 и
и
 - целые положительные числа, - как нетрудно
заметить, ничем не отличается по своим
результатам от получения неполных
частных с помощью алгоритма Евклида
(см. формулу (6)). Он должен поэтому
оборваться при
- целые положительные числа, - как нетрудно
заметить, ничем не отличается по своим
результатам от получения неполных
частных с помощью алгоритма Евклида
(см. формулу (6)). Он должен поэтому
оборваться при
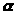 рациональном. При
рациональном. При
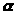 иррациональном этот процесс должен
быть бесконечным. Действительно, если
бы при каком-нибудь
иррациональном этот процесс должен
быть бесконечным. Действительно, если
бы при каком-нибудь
 было целым числом, то- отсюда следовало
бы, что
было целым числом, то- отсюда следовало
бы, что
 было
бы рациональным, что в свою очередь
влекло бы за собой рациональность
было
бы рациональным, что в свою очередь
влекло бы за собой рациональность
 >
>и т. д. и, наконец,
рациональность
>
>и т. д. и, наконец,
рациональность
 .
Из формул (23), делая
последовательные замены, исключая
.
Из формул (23), делая
последовательные замены, исключая
 ,
, ,
, ,
, мы получим цепную дробь
мы получим цепную дробь

(24)
к оторую,
так как
оторую,
так как
 можно взять сколь угодно большим, можно
записывать и в форме бесконечной цепной
дроби
можно взять сколь угодно большим, можно
записывать и в форме бесконечной цепной
дроби
Т е о р е м а III.
При любом целом
положительном
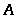 и иррациональном
и иррациональном
 уравнение (20)
уравнение (20)

имеет нетривиальное
решение ,
,
 ,
,
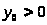 .
.
Рассмотрим уравнение общего вида,
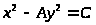 (25)
(25)
где
 - целое,
- целое,
 - целое число,
- целое число,
 - иррациональное число. При
- иррациональное число. При
 это уравнение всегда имеет бесчисленное
множество решений в целых числах
это уравнение всегда имеет бесчисленное
множество решений в целых числах
 и
и
 .
При произвольных
.
При произвольных
 и
и
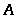 такое уравнение может вообще не иметь
решений.
такое уравнение может вообще не иметь
решений.
П р и м е р. Покажем, что уравнение
 (26)
(26)
вообще не разрешимо в
целых числах
 и
и
 .
Заметим, прежде всего,
что квадрат нечетного числа при Делений
на 8 всегда дает в остатке 1. Действительно,
так как всякое нечетное число а может
быть записано в форме
.
Заметим, прежде всего,
что квадрат нечетного числа при Делений
на 8 всегда дает в остатке 1. Действительно,
так как всякое нечетное число а может
быть записано в форме
 ,
где
,
где
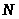 - целое число, то
- целое число, то
 ,
(27)
,
(27)
где
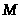 - целое число в силу того, что или
- целое число в силу того, что или
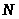 ,
или
,
или
 должно быть четным числом. Далее, если
должно быть четным числом. Далее, если
 -
решение уравнения (27),.
то
-
решение уравнения (27),.
то
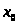 и
и
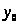 не могут быть числами одинаковой
четности. Если бы
не могут быть числами одинаковой
четности. Если бы
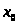 и
и
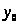 были одновременно четными или нечетными,
то
были одновременно четными или нечетными,
то
 было бы четным числом и не могло быть
равно 1. Если же
было бы четным числом и не могло быть
равно 1. Если же
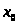 нечетно, а
нечетно, а
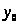 четно, то при делении на
четно, то при делении на
 давало бы в остатке 1,
давало бы в остатке 1,
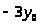 делилось бы на 4 и
делилось бы на 4 и
 при делении на 4 давало бы в остатке 1.
Это невозможно, так как при делении на
4 правая часть тривиально дает в остатке
при делении на 4 давало бы в остатке 1.
Это невозможно, так как при делении на
4 правая часть тривиально дает в остатке
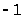 или
или
 .
Наконец, если
.
Наконец, если
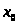 четно, а
четно, а
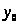 нечетно, то
нечетно, то
 делится на 4,
делится на 4,
 на основании (26) может быть записано в
форме
на основании (26) может быть записано в
форме
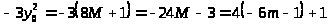
и, значит, при делении на 4
дает в остатке 1. Поэтому
 при делении на 4 должно опять давать в
остатке 1, что, как мы уже видели,
невозможно. Поэтому не существует целых
чисел
при делении на 4 должно опять давать в
остатке 1, что, как мы уже видели,
невозможно. Поэтому не существует целых
чисел
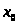 и
и
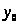 ,
которые могли бы удовлетворять уравнению
(26).
,
которые могли бы удовлетворять уравнению
(26).
Не останавливаясь на вопросе,
при каких условиях, наложенных на
 и
и
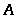 ,
уравнение (25) будет иметь
решение, - вопросе трудном и разрешимом
с помощью общей теории квадратических
иррациональностей в алгебраической
теории чисел, - мы остановимся на случае,
когда уравнение (25) имеет нетривиальные
решения. По-прежнему нетривиальным
решением мы будем называть решение
,
уравнение (25) будет иметь
решение, - вопросе трудном и разрешимом
с помощью общей теории квадратических
иррациональностей в алгебраической
теории чисел, - мы остановимся на случае,
когда уравнение (25) имеет нетривиальные
решения. По-прежнему нетривиальным
решением мы будем называть решение
 ,
если
,
если
 .
Итак, пусть уравнение (25) имеет нетривиальное
решение
.
Итак, пусть уравнение (25) имеет нетривиальное
решение
 ;
другими словами, пусть
;
другими словами, пусть
 (28)
(28)
Рассмотрим при том же
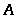 уравнение
уравнение
 (29)
(29)
Это уравнение имеет
бесчисленное множество решений в целых
числах при
 и иррациональном
и иррациональном
 ,
и любое такое его решение
,
и любое такое его решение
 будет:
будет:
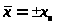 ,
,
 ,
,
Так как
 решение уравнения (29)
решение уравнения (29)
 .
.
Равенство (28) в свою очередь может быть переписано в форме
 .
.
Перемножая почленно эти два последних равенства, мы получаем
 (30)
(30)
Но

и совершенно так же
 .
.
Воспользовавшись этими двумя равенствами, мы можем переписать равенство (30) в форме

или в форме
 .
.
Этим мы доказали, что если
 - решение уравнения (25), то этому уравнению
будет удовлетворять и пара чисел
- решение уравнения (25), то этому уравнению
будет удовлетворять и пара чисел
 :
:
 ,
,
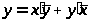 ,
(31)
,
(31)
где
 - любое решение уравнения (29). Таким
образом, мы доказали, что если
уравнение (25) имеет
хотя бы одно решение, то оно имеет их
бесчисленное множество.
- любое решение уравнения (29). Таким
образом, мы доказали, что если
уравнение (25) имеет
хотя бы одно решение, то оно имеет их
бесчисленное множество.
Нельзя, конечно, утверждать,
что формулами (31) даются
все решения уравнения (25). В теории
алгебраических чисел доказывается, что
все решения уравнения (25) в целых числах
можно получить, взяв некоторое конечное
и определенное зависящее от
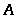 и
и
 число решений этого уравнения и размножив
их с помощью формул (31). Уравнение (25) при
А отрицательном
или равном квадрату целого числа может
иметь не более конечного числа решений.
Решение самых общих уравнений второй
степени с двумя неизвестными в целых
числах, уравнений вида
число решений этого уравнения и размножив
их с помощью формул (31). Уравнение (25) при
А отрицательном
или равном квадрату целого числа может
иметь не более конечного числа решений.
Решение самых общих уравнений второй
степени с двумя неизвестными в целых
числах, уравнений вида
 (32)
(32)
где числа А, В, С, D, Е и F - целые, сводится с помощью замен переменных к решению уравнений вида (25) с положительным или отрицательным А. Поэтому характер поведения решений, если они существуют, такой же, как и у уравнения типа (25). Подводя итог всему изложенному, мы можем теперь сказать, что уравнение второй степени с двумя неизвестными типа (32) может не иметь решений в целых числах, может иметь их только в конечном числе и, наконец, может иметь бесконечное множество таких решений, причем эти решения берутся тогда из конечного числа обобщенных геометрических прогрессий, даваемых формулами (31).
ПРОГРАММА №1 (УРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ)

n – степень многочлена;
a – коэффициент при x;
c – свободный член уравнения;
d – делитель свободного члена;
w – вспомогательная переменная
для возведения d в степень
аргумента;
x – сумма возведенных d
в степень аргумента
умноженных на a
program matan_1;
uses crt;
var i,n,c,j,k,x,w,q,p:integer; a,d:array[1..100] of integer;
BEGIN
writeln ('введите степень многочлена');
readln (n);
for i:=1 to n+1 do begin
if i=n+1 then begin writeln ('введите свободный коэффициент');
read (c);end;
if i<>n+1 then begin Writeln ('введите коэффициент при x^',n-i+1);
readln (a[i]); end;end;
w:=1;
for j:=1 to c do begin
if c/j= (c div j) then begin d[j]:=-j;
k:=n;
for i:=1 to n do begin
for q:=1 to k do
w:=w*d[j];
x:=x+w*a[i];
k:=k-1;w:=1;end;
if x+c=0 then begin p:=p+1;
writeln('целый корень уравнения =',d[j]);end;
end; x:=0;end;
for j:=1 to c do begin
if c/j= (c div j) then begin d[j]:=j;
k:=n;
for i:=1 to n do begin
for q:=1 to k do
w:=w*d[j];
x:=x+w*a[i];
k:=k-1;w:=1;end;
if x+c=0 then begin p:=p+1;
writeln('целый корень уравнения =',d[j]);end;
end; x:=0;end;
if p=0 then writeln ('данное уравнение в целых числах неразрешимо');
readln;readln;
END.
ПРОГРАММА №2 (Уравнения первой степени с двумя неизвестными)
program matan_2;
var p,q,t,n,i,k,x,y,w,r,s,d:integer; a,b,c:array[1..1000]of integer;
BEGIN
writeln('вв. при х'); readln(p);
writeln('вв. при y'); readln(q);
writeln('вв. c'); readln(t);
if p<0 then x:=-p else x:=p; if q<0 then y:=-q else y:=q;
n:=0;n:=0;k:=1;
for i:=1 to 10 do begin
if k<>0 then begin n:=n+1;
for i:=n to n do begin
a[i]:=x; b[i]:=y;
c[i]:=x div y;
x:=x-c[i]*y;
k:=k+1;n:=0;r:=r+1;
if (x<y) and (x<>1) then begin w:=y; y:=x; x:=w;end else k:=0;
end;
end;end;
x:=p;y:=q;
for i:=1 to r do begin
a[i]:=x; b[i]:=y;
c[i]:=x div y;
x:=x-c[i]*y;a[i]:=1;b[i]:=1;
if (x<y) and (x<>1) then begin w:=y; y:=x; x:=w;end;
end;
for i:=r downto 1 do begin
b[r]:=0;
b[i]:=c[i]*b[i]+a[i];
if i>1 then b[i-1]:=b[i];
if i>2 then a[i-2]:=b[i-1];
end;
if (p*b[1]+q*a[1]+t)=0 then begin
writeln('корни уравнения x=',b[1],'y=',a[1]);
writeln ('все его решения будут содержаться в прогрессиях');
writeln('x=',b[1],'+',q,'*','t');
writeln('y=',a[1],'+',p,'*','t');end;
readln;
END.
ЗАКЛЮЧЕНИЕ
Сравнивая поведение и характер решений уравнений второй степени с двумя неизвестными в целых числах с поведением решений уравнений первой степени, мы можем установить одно весьма существенное обстоятельство. Именно, если решения уравнения первой степени, когда они существуют, образуют арифметические прогрессии, то решения уравнения второй степени, когда их имеется бесконечно много, берутся из конечного числа обобщенных геометрических прогрессий. Другими словами, в случае второй степени пары целых чисел, которые могут быть решениями уравнения, встречаются значительно реже, чем пары целых чисел, которые могут быть решениями уравнения первой степени. Это обстоятельство не случайно. Оказывается, что уравнения с двумя неизвестными степени выше второй, вообще говоря, могут иметь только конечное число решений. Исключения из этого правила крайне редки.
СПИСОК ЛИТЕРАТУРЫ:
1. Гельфонд А.О. Решение уравнений в целых числах. -4-е изд. –
М.: Наука, 1983. – 64 с. – (Популярные лекции по математике).
3


