Решение задачи линейного программирования
Решение задачи линейного программирования.
Рассмотрим задачу линейного программирования
 (1)
(1)
Теорема. Если
множество
 планов задачи (1) не пусто и целевая
функция
планов задачи (1) не пусто и целевая
функция
 сверху ограничена на этом множестве,
то задача (1) имеет решение.
сверху ограничена на этом множестве,
то задача (1) имеет решение.
Теорема. Если
множество
 допустимых планов имеет крайние точки
и задача (1) имеет решение, то среди
крайних точек найдется оптимальная.
допустимых планов имеет крайние точки
и задача (1) имеет решение, то среди
крайних точек найдется оптимальная.
Метод исключения Жордана-Гаусса для системы линейных уравнений.
Большинство из существующих численных методов решения задач линейного программирования использует идею приведения системы линейных уравнений

которая в матричной форме
записывается в виде
 ,
к более удобному виду с помощью так
называемого метода Жордада-Гаусса.
,
к более удобному виду с помощью так
называемого метода Жордада-Гаусса.
В первом уравнении системы
отыскивается коэффициент
 ,
отличный от нуля. С помощью этого
коэффициента обращаются в нуль
коэффициенты при переменной
,
отличный от нуля. С помощью этого
коэффициента обращаются в нуль
коэффициенты при переменной
 в остальных уравнениях системы. Для
этого первое уравнение умножается на
число
в остальных уравнениях системы. Для
этого первое уравнение умножается на
число
 и прибавляется к уравнению с номером
и прибавляется к уравнению с номером
 ,
,
 .
Затем первое уравнение делится на число
.
Затем первое уравнение делится на число
 .
Это преобразование называется элементарным
преобразованием. Полученная эквивалентная
система обладает тем свойством, что
переменная
.
Это преобразование называется элементарным
преобразованием. Полученная эквивалентная
система обладает тем свойством, что
переменная
 присутствует только в первом уравнении,
и притом с коэффициентом 1. Переменная
присутствует только в первом уравнении,
и притом с коэффициентом 1. Переменная
 называется базисной переменной.
называется базисной переменной.
Аналогичная операция совершается поочередно с каждым уравнением системы; при этом всякий раз преобразуются все уравнения и выполняется список базисных переменных.
Результатом применения метода Жордада-Гаусса является следующее: либо устанавливается, что система несовместна, либо выявляются и отбрасываются все «лишние» уравнения; при этом итоговая система уравнений имеет вид
 ,
,
 ,
,
где
 — список номеров базисных переменных,
— список номеров базисных переменных,
 — множество номеров небазисных
переменных. Здесь
— множество номеров небазисных
переменных. Здесь
 — ранг матрицы
— ранг матрицы
 коэффициентов исходной системы уравнений.
коэффициентов исходной системы уравнений.
Полученную системы уравнений
называют приведенной системой,
соответствующей множеству
 номеров базисных переменных.
номеров базисных переменных.
Симплекс-метод.
Симплекс –метод, метод последовательного улучшения плана, является в настоящее время основным методом решения задач ЛП.
Рассмотрим каноническую задачу ЛП
 (2)
(2)
где векторы
 ,
матрица
,
матрица
 и
и
 .
Множество планов в задаче (2) будем
обозначать через
.
Множество планов в задаче (2) будем
обозначать через
 и будем предполагать, что все угловые
точки
и будем предполагать, что все угловые
точки
 являются невырожденными.
являются невырожденными.
 ,
где вектор
,
где вектор
 определяется формулой
определяется формулой
 .
.
Теорема. Если в
угловой точке
 выполняется условие
выполняется условие
 ,
то
,
то
 — решение задачи (2).
— решение задачи (2).
Теорема. Для того,
чтобы угловая точка
 являлась решением задачи (2), необходимо
и достаточно, чтобы в ней выполнялось
условие
являлась решением задачи (2), необходимо
и достаточно, чтобы в ней выполнялось
условие
 .
.
Алгоритм симплекс-метода.
Переход из старой угловой точки
 в новую угловую точку
в новую угловую точку
 состоит, в сущности, лишь в изменении
базисной матрицы
состоит, в сущности, лишь в изменении
базисной матрицы
 ,
в которую вместо вектора
,
в которую вместо вектора
 вводится вектор
вводится вектор
 .
Новая базисная матрица может быть теперь
использована для вычисления базисных
компонентов вектора
.
Новая базисная матрица может быть теперь
использована для вычисления базисных
компонентов вектора
 .
Таким образом, алгоритм симплекс-метода
может быть представлен в следующей
форме.
.
Таким образом, алгоритм симплекс-метода
может быть представлен в следующей
форме.
Шаг 0. Задать
целевой вектор
 ,
матрицу условий
,
матрицу условий
 ,
вектор ограничений
,
вектор ограничений
 и множество базисных индексов
и множество базисных индексов
 .
Сформировать базисную матрицу
.
Сформировать базисную матрицу
 и вектор
и вектор
 .
.
Шаг 1.
Вычислить матрицу
 и вектор
и вектор
 .
.
Шаг 2.
Вычислить вектор потенциалов
 и оценки
и оценки
 .
.
Шаг 3. Если
 для всех
для всех
 ,
то остановиться: вектор
,
то остановиться: вектор
 — базисный вектор оптимального плана;
иначе перейти на шаг 4.
— базисный вектор оптимального плана;
иначе перейти на шаг 4.
Шаг 4.
Выбрать произвольный индекс
 и вычислить вектор
и вычислить вектор
 .
.
Шаг 5. Если
 ,
то остановиться:
,
то остановиться:
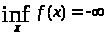 ;
иначе перейти на шаг 6.
;
иначе перейти на шаг 6.
Шаг 6.
Сформировать множество индексов
 и вычислить
и вычислить
 .
.
Шаг 7. В
множестве
 индекс
индекс
 заменить на индекс
заменить на индекс
 ,
в матрице
,
в матрице
 — вектор
— вектор
 — на вектор
— на вектор
 ,
в векторе
,
в векторе
 — компоненту
— компоненту
 на
на
 .
Перейти на шаг 1.
.
Перейти на шаг 1.
1