Программа государственного экзамена по математике для студентов математического факультета Московского городского педагогического университета
Программа государственного экзамена по математике
для студентов математического факультета
Московского городского педагогического университета
Алгебра и теория чисел
1. Группы; примеры и простейшие свойства элементов группы.
2. Кольца и поля; примеры и простейшие свойства элементов.
3. Арифметические функции: (n), (n), (n).
4. Алгоритм Евклида и его применения.
5. Сравнения и их свойства. Теоремы Эйлера и Ферма.
6. Базис и размерность векторного пространства.
7. Основные теоремы о системах линейных уравнений.
8. Корни многочлена, теорема Безу, схема Горнера.
9. Разложение многочлена над полем в произведение
неприводимых множителей и его единственность.
10. Теорема о строении простого алгебраического расширения.
1. Группы; примеры и простейшие свойства элементов группы
10. Определение группы.
Всюду в дальнейшем запись (G, ) означает, что на непустом множестве G задана операция “”.
Определение. Множество (G, ) называется группой, если выполнены следующие условия:
(1) операция “” ассоциативна, т.е. (x, y, zG) (xy)z = x(yz);
(2) множество G обладает нейтральным элементом относительно операции :
(eG)(xG) xe = ex = x;
(3) каждый элемент множества G обладает симметричным элементом:
(xG) (yG) xy = yx = e.
20. Примеры групп: числовые группы, группы симметрий геометрических фигур, группы подстановок, матричные группы.
Примеры групп весьма разнообразны. Перечислим некоторые из них.
1. Числовые группы (группы, элементы которых являются комплексными числами).
а) Аддитивные группы целых чисел Z, рациональных чисел Q, действительных чисел R, комплексных чисел C.
б) Мультипликативные группы ненулевых рациональных чисел Q*, ненулевых действительных чисел R*, ненулевых комплексных чисел C*, положительных рациональных чисел Q>+>, положительных действительных чисел R>+>.
2. Группы подстановок S(X) и S>n>, действующих на множестве X, в частности, на множестве {1, 2, . . . , n}.
3. Группы движений геометрических фигур. Пусть Ф - какая-нибудь геометрическая фигура на плоскости, O(Ф) - множество движений плоскости, переводящих фигуру Ф на себя. Множество O(Ф) относительно операции композиции (последовательного выполнения) движений является группой. Элементы множества O(Ф) часто называются симметриями фигуры Ф.
Рассмотрим, например, группу симметрий правильного треугольника.

 ;
их удобно обозначить ,
,
.
Для описания умножения элементов группы
(G, )
можно использовать так называемую
таблицу Кэли (таблицу умножения группы).
;
их удобно обозначить ,
,
.
Для описания умножения элементов группы
(G, )
можно использовать так называемую
таблицу Кэли (таблицу умножения группы).
Для группы симметрий правильного треугольника таблица Кэли имеет вид:
-
Заметим, что вращения перемножаются по правилу 2 = , 3 = . Далее, квадрат любого отражения равен .
Легко проверить, что = , = . Кроме того, = .
Остальные произведения в таблице легко восстановить, используя, например, групповую структуру операции. В частности, имеем:
=() = 2 = = ;
=() = () = 2 = .
4. Группы геометрических преобразований. Группы вращений, подобий, гомотетий с заданным общим центром, параллельных переносов.
5. Матричные группы. Укажем на две важнейшие матричные группы:
GL>n>(R) - полная линейная группа (группа обратимых матриц),
SL>n>(R) - специальная линейная группа
(группа матриц с единичным определителем),
30. Арифметика группы: обратные элементы, степени с целым показателем.
При описании таблицы Кэли группы симметрий правильного треугольника мы использовали так называемые арифметические свойства элементов группы. Отметим важнейшие из них в следующей теореме.
Теорема. Пусть (G,) - группа. Тогда для ее элементов справедливы равенства:
(а) (xy)(zt) = x(y(zt) = ((xy)z)t;
(б) (xy)-1 = y-1x-1;
(в) (xp)q = xpq; xpxq = xp+q для любых целых p, q.
Доказательство. Проверим только пункт (б). Имеем:
(xy)(y-1x-1) = x(yy-1)x-1 = x(1)x-1 = 1,
(y-1x-1)(xy) = y-1(x-1x)y = y-1(1)y = 1;
откуда и получаем требуемое утверждение.
40. Решение в группах линейных уравнений. В качестве применения простейших свойств приведем следующий простой результат.
Теорема. В произвольной мультипликативной группе G однозначно разрешимо каждое из уравнений:
ax = b, ya = b, где a, b - фиксированные элементы группы.
Доказательство. Допустим, что элемент g удовлетворяет равенству ag = b. Тогда умножая обе части равенства слева на элемент обратный к g, получим
a-1(ag) = a-1b, откуда находим g = a-1b. Легко проверить, что элемент a-1b является решением уравнения ax = b, т.е. справедливо равенство a(a-1b) = b.
Аналогично доказывается разрешимость второго уравнения.
Примеры. 1. Решить уравнение (12)x = (13) в группе подстановок S>3>.
Имеем: x = (12)(13) = (123).
2. Решить уравнение x = в группе симметрий правильного треугольника.
Имеем: x = -1 = , поскольку является отражением и
C() = (C) = B = C.
3. Решить уравнение
X
 =
=
 в
группе GL>2>(R).
в
группе GL>2>(R).
Имеем:
X
=

 =
=
 =
= .
.
2. Кольца и поля; примеры и простейшие свойства элементов
10. Определение кольца и поля.
Определение. Непустое множество A, на котором заданы операции сложения и умножения, называется кольцом, если выполнены следующие два условия:
а) (A, +) - абелева группа;
б) умножение дистрибутивно относительно сложения, т.е. для любых элементов x, y, z из A выполнены равенства: (x + y)z = xz + yz; x(y + z) = xy + xz.
Определение. Кольцо называется коммутативным, если операция умножения в нем коммутативна; кольцо называется ассоциативным, если операция умножения в нем ассоциативна. Кольцо называется кольцом с единицей, если оно обладает нейтральным элементом относительно умножения.
Определение. Пусть A - ассоциативное кольцо с единицей 1. Элемент aA называется обратимым, если существует элемент bA такой, что ab = ba = 1.
Легко проверить, что элемент b, о котором идет речь находится однозначно, поэтому он обозначается a-1 и называется элементом обратным к a.
Важнейшим типом колец являются поля.
Определение. Ассоциативно-коммутативное кольцо с единицей называется полем, если в нем всякий ненулевой элемент обратим.
20. Примеры колец: числовые кольца, кольца многочленов, кольца последовательностей и функций, кольца матриц, кольца вычетов.
Если группы появляются, прежде всего, как группы обратимых отображений, то возникновение понятия кольца связано с изучением важнейших числовых систем и многочленов.
1. Числовые кольца (кольца, элементы которых являются комплексными числами):
а) (классические числовые кольца) кольцо целых чисел Z, кольцо рациональных чисел Q, кольцо действительных чисел R, кольцо комплексных чисел C.
б) кольцо Z[i] целых гауссовых чисел вида a + bi, где a, b - целые числа;
г) кольцо Z[ ]
действительных чисел вида a
+ b
]
действительных чисел вида a
+ b с целыми a,
b.
с целыми a,
b.
2. Кольца многочленов R[x], Q[x], Z[x], C[x] от одной переменной x с действительными, рациональными, целыми и комплексными коэффициентами.
3. Кольца последовательностей и функций. Среди этих колец выделим особо:
а) кольцо последовательностей действительных чисел с обычными операциями сложения и умножения последовательностей;
б) кольцо ограниченных последовательностей действительных чисел;
в) кольцо фундаментальных последовательностей;
г) кольцо непрерывных действительно-значных функций на отрезке [0 , 1].
4. Кольца матриц. Среди разнообразных матричных колец выделим следующие:
а) полное матричное кольцо M>n>(A) над кольцом A или кольцо квадратных матриц порядка n с элементами из кольца A, в качестве кольца коэффициентов A можно рассматривать, в частности, любое числовое кольцо;
б) кольцо D>n>(A) диагональных матриц, т.е. матриц, у которых вне главной диагонали находятся только нулевые элементы;
в) кольцо TN>n>(A) нильтреугольных матриц, т.е. треугольных матриц с нулями на главной диагонали.
Кольца M>n> и TN>n> являются некоммутативными, в кольце TN>n> нет единицы.
30. Примеры полей.
1. Числовые поля.
Q,
R,
C,
Q[i],
Q[ ]
.
]
.
2. Поля
дробно-рациональных функций:
Q(x),
R(x),
C(x).
Так, элементами множества R(x)
являются всевозможные функции вида
 ,
где f(x),
g(x)
- многочлены с действительными
коэффициентами, причем многочлен g(x)
ненулевой. Операции сложения и умножения
дробей обычные.
,
где f(x),
g(x)
- многочлены с действительными
коэффициентами, причем многочлен g(x)
ненулевой. Операции сложения и умножения
дробей обычные.
3. Поле вычетов Z>p >по простому модулю p. Например, для p=7 утверждение получается из следующих равенств в кольце Z>7>: 24 = 35 = 66 = 1.
40. Арифметика колец и полей. Важнейшие арифметические свойства элементов колец и полей приведены в теоремах.
Теорема. Для любых элементов кольца справедливы равенства:
(а) 0x = x0 = 0;
(б) правило знаков: x(- y) = (-x)y = -(xy);
(в) (дистрибутивность умножения относительно разности)
(x - y)z = xz - yz, x(y - z) = xy - xz;
где разность определяется обычным образом x - y := x + (- y).
Доказательство. (а) Имеем: 0x = (0 + 0)x = 0x +0x, откуда 0x = 0. Аналогично проверяется и второе равенство x0 = 0.
(б) Имеем: 0 = x0 = x(y + (-y)) = xy +x(-y), откуда x(-y) = -(xy).
(в) Имеем: (x - y)z =(x + (- y))z = xz + (-y)z = xz - yz.
Обозначение.
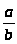 := ab-1,
если a, b
- элементы поля, причем b
0.
:= ab-1,
если a, b
- элементы поля, причем b
0.
Теорема. В поле справедливы обычные правила работы с дробями:
(а) основное свойство
дроби: (c0)
 ;
;
(б) правила сложения
дробей:
 ,
,
 ;
;
(в) правило умножения
дробей:
 ;
;
(г) ,
если ab
0;
,
если ab
0;
в частности, справедливо известное правило деления дробей.
Доказательство. (а) Действительно,
 =
(ac)(bc)-1
= acc-1b =
ab-1
=
=
(ac)(bc)-1
= acc-1b =
ab-1
=
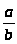 .
.
(б)
Имеем:
 = (a + c)b-1
= ab-1
+ cb-1
=
= (a + c)b-1
= ab-1
+ cb-1
=
 .
И далее на основании уже
доказанных свойств получаем
.
И далее на основании уже
доказанных свойств получаем
 .
.
Аналогично проверяются и два оставшихся пункта.
3. Арифметические функции: (n), (n), (n).
10. Полная мультипликативность.
Определение. Числовой (арифметической) функцией называется функция, определенная на множестве Z>+> целых положительных чисел и принимающая комплексные значения.
Числовая функция называется вполне мультипликативной, если выполнены условия:
(1) (x) (x)0,
(2) для любых взаимно простых чисел x и y
(xy)= (x) (y).
Заметим, что непосредственно из определения вытекает равенство
(1)=1.
В самом деле, (1)0, так как иначе данная функция была бы нулевой; (1)= (11)= (1) (1), следовательно, (1)=1.
Легко проверить, что каждая из следующих функций
(x)=1, (x)= x, (x)= x-1,
вполне мультипликативна.
Следующая теорема позволяет существенно расширить запас вполне мультипликативных функций.
Теорема. Произведение вполне мультипликативных функций является вполне мультипликативной функцией.
Доказательство. Пусть числа x и y взаимно просты, а функции f и g вполне мультипликативны. Тогда, обозначив через h произведение функций f и g, имеем:
h(xy)=f(xy)g(xy)=f(x)f(y)g(x)g(y)=[f(x)g(x)][f(y)g(y)]=
=h(x)h(y).
Следствие. Для любого целого k функция (x)= xk вполне мультипликативна.
20. Сумма значений функции по всем делителям аргумента.
Введем в рассмотрение, наряду с функцией (x), функцию
 ,
,
равную сумме всех значений функции (d) при условии, что переменная d пробегает все делители числа x.
Теорема (основное тождество).
Если x= ,
то
,
то

 .
.
В частности,
если функция
вполне мультипликативна,
то и функция
 также вполне мультипликативна.
также вполне мультипликативна.
Доказательство. Рассмотрим произведение сумм, находящееся в правой части требуемого равенства:

 =
=
= =
= .
.
Осталось заметить, что для каждого набора (>1>, >2>,..., >k>> >) целых неотрицательных чисел >i>, не превосходящих a>i>, в сумме

каждое
слагаемое встречается ровно один раз.
Учитывая теперь, что каждый делитель
числа
 имеет
вид
имеет
вид
 ,
получаем
,
получаем
 =
= .
.
Свойство полной мультипликативности рассматриваемой функции немедленно вытекает из того, что взаимно простые числа содержат различные простые сомножители.
30. Число делителей (x) и сумма делителей (x).
Рассмотрим следующие вполне мультипликативные функции:
(x)=
 ,
где (x)=1,
- число делителей числа x,
,
где (x)=1,
- число делителей числа x,
(x)=
 ,
где (x)
= x, - сумма
делителей числа x.
,
где (x)
= x, - сумма
делителей числа x.
Теорема. Справедливы тождества:
( )=(a>1>
+ 1)( a>2
>+ 1)...(
a>k>
+ 1),
)=(a>1>
+ 1)( a>2
>+ 1)...(
a>k>
+ 1),
( )=
)= .
.
Доказательство. а) Из определения функции (x) немедленно следует указанное тождество, поскольку в силу основного тождества легко подсчитать число слагаемых, каждое из которых равно 1, в каждой из скобок соответствующего произведения.
б) Это тождество получается из основного тождества и формулы суммы членов геометрической прогрессии:

 .
.
40. Функция Эйлера. Одной из важнейших числовых функций является следующая функция, впервые введенная в рассмотрение Эйлером.
Определение. Через (x) обозначается количество чисел ряда
1, 2, ..., x, (*)
взаимно простых с числом x.
Справедлива следующая теорема, которую приведем без доказательства.
Теорема. Если
x= ,
то
,
то
(x)=
x
 .
.
Следствие. Функция Эйлера вполне мультипликативна и
 .
.
Теорема (тождество Гаусса).
 .
.
Доказательство. Применяя основное
тождество и последнее следствие,
получаем, считая
 ,
,

 .
.
4. Алгоритм Евклида и его применения
10. Алгоритм Евклида. Наибольший общий делитель чисел a, b можно найти с помощью алгоритма Евклида, который состоит в следующем.
Пусть b>0. Разделим a на b, тогда по теореме о делении с остатком:
a = bq>1> + r>1>.
Если r>1> = 0, то НОД(a, b) = b.
Если r>1 > 0, то разделим b с остатком на r>1>:
b = r>1>q>2> + r>2>.
Если r>2> = 0, то процесс деления закончим, а если r>2 > 0, то разделим r>1 >с остатком на r>2>> >:
r>1 > = r>2>q>3 > + r>3>.
Продолжая далее таким же образом, мы закончим процесс деления как только получится остаток равный 0.
Заметим, что такой остаток обязательно получится. В самом деле, остаток всегда меньше делителя,> >поэтому b > r>1 >> r>2 >> >> r>3 >> . . . и число получаемых остатков не превосходит b.
Итак, в результате указанного алгоритма получим, что:
|
|
a > >= > >bq>1 > + r>1> , |
|
|
b> > = r>1 >q>2 > + r>2> , |
||
|
r>1 > = r>2 >q>3 > + r>3> , |
(1) |
|
|
. . . . . . . . . . . . . |
||
|
r>n>>-2 > = r>n-1>> >q>n-1>> >+ r>n> , |
||
|
r>n-1>> > = r>n>> >q>n> . |
Тогда на основании свойств 20 и 10 :
НОД(a, b) = НОД(b, r>1>) = НОД(r>1>, r>2>) = . . . = НОД(r>n-1>,> >r>n>) = r>n>.
Следовательно, наибольший общий делитель чисел a и b совпадает с последним ненулевым остатком r>n>> >в алгоритме Евклида для > >чисел a и b.
Пример. Найти НОД(160, 72).
Применим к данным числам алгоритм Евклида:
160 = 722 + 16, 72 = 164 + 8, 16 = 82. (2)
Следовательно, НОД(160, 72) = 8.
20. Теорема (о линейном представлении НОД). Если d - наибольший общий делитель чисел a и b, то существуют такие целые числа x и y, что выполняется равенство: d = xa + yb.
Допустим, что числа a и b связаны следующими соотношениями:
|
a > >= > >bq>1 > + r>1> , |
|
|
b> > = r>1 >q>2 > + r>2> , |
|
|
r>1 > = r>2 >q>3 > + r>3> , |
|
|
. . . . . . . . . . . . . |
|
|
r>n>>-2 > = r>n-1>> >q>n-1>> >+ r>n> . |
Докажем, что каждое из чисел r>k> линейно выражается через a и b с целыми коэффициентами. Для r>1> утверждение тривиально: r>1> = a - bq>1 >. Считая, что каждое из чисел r>1> , r>2> , . . . , r>n-1> является целочисленной линейной комбинацией чисел a и b (r>k> = >k> a + >k>> >b), имеем
r>n> = >n-2> a + >n-2 >b - (>n-1> a + >n-1 >b) q>n-1> = (>n-2> - >n-1>) a + (>n-2 >- >n-1 >q>n-1>)b.
Пример. Найти линейное представление НОД(160, 72).
Решение. Из второго равенства системы (2) следует, что 8 = 72 - 164, а из первого равенства получим, что 16 = 160 - 722. Из двух полученных равенств находим: 8 = 72 - 16 4 = 72 - (160 - 72 2) 4 = (-4) 160 + 9 72.
Таким образом, искомое представление НОД имеет вид:
8 = (-4) 160 + 9 72.
30.
Связь алгоритма Евклида с непрерывными
дробями. Пусть
- рациональная несократимая дробь
 .
Для разложения числа
в непрерывную цепную дробь можно
воспользоваться алгоритмом Евклида:
.
Для разложения числа
в непрерывную цепную дробь можно
воспользоваться алгоритмом Евклида:


Следовательно,
 , откуда
, откуда
Непрерывные дроби можно использовать для решения различных теоретико-числовых задач.
1. Линейное представление наибольшего общего делителя
Пример 1. Найти линейное представление наибольшего общего делителя чисел (59, 163).
Решение.
Разложим в непрерывную дробь число :
:
 =
[2; 1, 3, 4, 1, 2].
=
[2; 1, 3, 4, 1, 2].
Cледовательно, можно теперь заполнить таблицу:
-
q>s>
2
1
3
4
1
2
P>s>
1
2
3
11
47
58
163
Q>s>
0
1
1
4
17
21
59
>s>
+1
-1
+1
-1
+1
-1
Отсюда получаем 59 58 - 163 21 = -1 или 59 (-58) + 163 21 = 1.
2. Решение линейных диофантовых уравнений
Как практически находить какое-нибудь решение линейного неопределенного уравнения
ax + by = c при (a, b)=1, c=1 ?
Можно воспользоваться алгоритмом
Евклида, из которого легко получить
линейное представление НОД чисел a,
b, или
представить дробь
 в виде последней подходящей
в виде последней подходящей
 ,
откуда aQ>n>
- bP>n >=
(-1)n
.
,
откуда aQ>n>
- bP>n >=
(-1)n
.
Пример. Решить диофантово уравнение 163x + 59y = 1.
Решение. Мы проверили раньше, что 163 21 + 59 (-58) = 1, следовательно, общее решение имеет вид:

6. Базис и размерность векторного пространства
10.
Линейные комбинации и линейные оболочки
векторов. Выражение вида
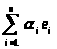 =
>1>e>1>
+ . . . + >n>e>n>,
где >i
>- числа, e>i>
- векторы из пространства V, называется
линейной комбинацией векторов
e>i>;
числа >i>
называются коэффициентами линейной
комбинации.
=
>1>e>1>
+ . . . + >n>e>n>,
где >i
>- числа, e>i>
- векторы из пространства V, называется
линейной комбинацией векторов
e>i>;
числа >i>
называются коэффициентами линейной
комбинации.
Определение. Линейной оболочкой системы векторов E = (e>1>, . . . , e>n>) называется множество всевозможных линейных комбинаций векторов данной системы; обозначение L(E). Таким образом,
L(E)
=
 .
.
Заметим, что линейная оболочка системы векторов является линейным подпространством.
Говорят, что вектор v линейно выражается через систему E, если v L(E).
Отметим простейшие свойства линейных оболочек:
(а) Если W - подпространство в V, E W, то L(E) W;
(б) Линейная оболочка L(E) совпадает с пересечением всех линейных подпространств, содержащих систему E;
(в) L(E G) = L(E) + L(G), где сумма подпространств U и W определяется равенством U + W := { u + w u U, w W }.
20. Линейно независимые системы.
Линейная комбинация векторов называется тривиальной, если все ее коэффициенты равны 0. Значение тривиальной линейной комбинации равно 0.
Определение. Система векторов называется линейно независимой, если всякая ее нетривиальная линейная комбинация отлична от нуля.
Заметим, что для доказательства линейной независимости системы достаточно приравнять к нулю произвольную ее линейную комбинацию и вывести из этого равенство нулю всех ее коэффициентов.
Кроме того, система векторов является линейно зависимой, если некоторая ее нетривиальная линейная комбинация равна 0.
Нам потребуются в дальнейшем следующие две леммы, которые мы приведем без доказательства.
Лемма 1. Если система E линейно независима, а система Es (полученная присоединением вектора s к системе E) линейно зависима, то s линейно выражается через E.
Лемма 2 (основная лемма о линейной зависимости).
“Большая“ система линейно зависима, если она линейно выражается через “маленькую“.
30. Базис линейного пространства.
Определение 1. Система E называется базисом линейного пространства V (обозначение B(V)), если выполнены условия:
(а) E линейно независима;
(б) V = L(E), т.е. всякий вектор пространства V линейно выражается через E.
Наряду с данным определением можно привести и другие эквивалентные определения.
Определение 2. Максимальная линейно независимая система E называется базисом линейного пространства V.
Определение 3. Система E называется базисом линейного пространства V, если всякий вектор пространства V однозначно записывается в виде линейной комбинации векторов системы E.
Заметим, что указанные определения равносильны.
40. Размерность линейного пространства.
Определение. Линейное пространство называется конечномерным, если оно обладает конечным базисом.
Определение. Число элементов в каком-нибудь базисе линейного пространства V называется его размерностью; обозначение dimV. Нулевое пространство имеет по определению пустой базис и нулевую размерность.
Отметим прежде всего теорему о корректности определения размерности.
Теорема. Всякие два базиса одного конечномерного пространства содержат одинаковое число векторов.
Доказательство. Пусть E и G - два базиса пространства V. Эти системы векторов линейно эквивалентны, т.е. они линейно выражаются друг через друга. Если бы одна система была “большой”, а другая “маленькой”, то “большая” система оказалась бы линейно зависимой в силу основной леммы о линейной зависимости, значит, обе они содержат одинаковое число векторов.
Следствие.
(а) Размерность линейной оболочки L(E) равна рангу системы E (ранг системы - максимальное число ее линейно независимых векторов): dim L(E) = r(E).
(б) Всякая система векторов n-мерного линейного пространства, содержащая более n элементов линейно зависима.
50. Примеры.
1. Координатное пространство kn имеет стандартный базис из единичных векторов e>i> := (0, . . . , 0, 1, 0, . . . , 0) ( единица находится на месте с номером i), следовательно, dim kn = n. Можно доказать, что система из n векторов-строк образует базис пространства kn определитель этой системы отличен от нуля.
2. Базис пространства решений однородной системы линейных уравнений - это фундаментальная система решений.
3. Пространство матриц
 имеет стандартный
базис из матричных единиц E>ij>
(единица находится на месте с номером
(i, j),
следовательно,
имеет стандартный
базис из матричных единиц E>ij>
(единица находится на месте с номером
(i, j),
следовательно,
dim
 = nm.
= nm.
4. Пространства многочленов Q>n>[x] с рациональными коэффициентами степени не превосходящей n имеет следующие базисы:
а) стандартный базис вида 1, x, x2, . . . , xn;
б) базис Тейлора “в точке c”:
1, (x - c), (x - c)2, . . . , (x - c)n , где c - некоторое число;
в) [базис Лагранжа “в точке (c>1>, . . . , c>n+1>)”:
g>i>(x) = {(x - c>1>) . . . (x - c>i>)^ . . . (x - c>n+1>)}/ {(c>i> - c>1>) . . . (c>i> - c>i>)^ . . . (c>i> - c>n+1>)},
где c>1>, . . . , c>n+1> - попарно различные скаляры, а знак ^ означает отсутствие указанного множителя.]
Координаты многочлена f(x)
относительно стандартного базиса - это его коэффициенты;
относительно базиса Тейлора -
это строка
 ;
;
[относительно базиса Лагранжа - это строка (f(c>1>), . . . , f(c>n+1>)).]
5. Вещественное линейное пространство C имеет стандартный базис (1, i).
7. Основные теоремы о системах линейных уравнений
10. Исследование системы линейных уравнений.
Пусть задана система линейных уравнений: Ax = b, где A- основная матрица, x- столбец переменных, b - столбец свободных членов. С помощью элементарных преобразований строк в основной матрице можно построить максимальную систему единичных столбцов. Кроме того, удалим из расширенной матрицы нулевые строки. Тогда можно считать, что расширенная матрица системы уравнений имеет вид:
 ,
,
где в последней строке ведущий элемент обозначен через .
Для ненулевого числа возможны два случая:
(а) находится до черты, т.е. лежит в основной матрице. Следовательно, в этом случае мы можем написать общее решение совместной системы. Заметим, что все переменные будут связаны ранг основной матрицы равен числу переменных системы.
(б) находится после черты; тогда система несовместна и ранг основной матрицы меньше ранга расширенной матрицы на единицу.
Тем самым, мы доказали теорему.
Теорема. Пусть - ведущий элемент последней строки приведенной ступенчатой матрицы. Тогда
(а) система совместна находится до черты;
(б) система несовместна находится после черты;
(в) система является определенной находится до черты и все переменные связанные;
(г) система является неопределенной находится до черты и имеется хотя бы одна свободная переменная.
20. Критерии совместности и определенности.
Из приведенной теоремы немедленно вытекают следующие два критерия.
Критерий совместности (теорема Кронеккера-Капелли). Система Ax = b линейных уравнений является совместной ранг основной матрицы равен рангу расширенной матрицы, т.е. r(A) = r(Ab).
Критерий определенности. Система Ax = b линейных уравнений от n переменных является определенной ранг основной матрицы равен рангу расширенной матрицы и равен числу переменных в системе, т.е. r(A) = r(Ab) = n.
30. Связь между решениями совместной неоднородной и связанной с ней однородной системами линейных уравнений.
Допустим, что дана совместная система линейных уравнений:
-
Ax = b.
(1)
Пусть >0>, >1>, >2> - частные решения системы (1), - ее общее решение. Тогда справедливы равенства A>1>t = b, A>2>t = b. Вычитая почленно из первого второе, на основании известных свойств, получаем: 0 = A>1>t - A>2>t = A(>1>t - >2>t) = A(>1> - >2>)t, т.е. разность между двумя частными решения системы (1) является решением связанной с ней однородной системы
-
Ax = 0.
(2)
Если теперь - общее решение системы (2), то имеем A t = 0, следовательно,
b = b + 0 = A>0>t + A t = A(>0>t + t) = A(>0> + )t,
т.е. сумма частного решения системы (1) и общего решения системы (2) является решением системы (1).
Таким образом, справедлива
Теорема. Общее решение совместной неоднородной системы (1) является суммой частного решения системы (1) и общего решения системы (2).
Поскольку общее решение однородной системы может быть записано в виде линейной комбинации ФСР, то получаем, что общее решение системы (1) можно записать в следующей параметрической форме:
= >0 >+ >1>>1> + >2>>2> + . . . + >m>>m>,
где >0 > - какое-нибудь частное решение системы (1); >1>, >2>, . . . , >m> - ФСР системы (2),
>1>, >2>, . . . , >m> - действительные параметры; m = n - r(A).
8. Корни многочлена; схема Горнера; теорема Безу
10. Корни многочлена.
Определение. Число c называется корнем многочлена f, если f(c)=0.
Другими словами, число c является корнем многочлена f, если
a>0>cn > >+ a>1>cn-1 + ... + a>n> >- >>1>c + a>n> = 0.
Это равенство означает, что число c является корнем уравнения
a>0 >xn> >+ a>1>xn-1 + ... + a>n> >- >>1> x + a>n> = 0,
при подстановке вместо x числа c получается верное равенство. Поэтому корень многочлена f и корень соответствующего уравнения f(x) = 0 - это одно и то же.
Схема Горнера позволяет проверять, является ли данное число c корнем данного многочлена или нет: с ее помощью мы как раз и вычисляем значение f(c).
Если требуется проверить несколько значений c, то для экономии выкладок строят не три отдельные схемы, а одну - объединенную. Например, для многочлена
f = 3x5 - 5x4 - 7x2 + 12
и чисел c = 1,-1,2 составляется таблица
|
3 |
-5 |
0 |
-7 |
0 |
12 |
|
|
1 |
3 |
-2 |
-2 |
-9 |
-9 |
3 |
|
-1 |
3 |
-8 |
8 |
-15 |
15 |
-3 |
|
2 |
3 |
1 |
2 |
-3 |
-6 |
0 |
Конечно, при заполнении третьей и четвертой строки таблицы работает" только первая строка - строка коэффициентов многочлена f.
Мы видим, в частности, что из трех рассмотренных чисел только c = 2 является корнем данного многочлена.
20. Теорема Безу.
Теорема Безу. Пусть f - многочлен, c - некоторое число.
1. f делится на двучлен x - c тогда и только тогда, когда число c является его корнем.
2. Остаток от деления f на x - c равен f(c).
Доказательство. Сначала мы докажем второе утверждение. Для этого разделим f c остатком на x - c:
f = (x - c)q + r;
по определению остатка, многочлен r либо равен 0, либо имеет степень, меньшую степени x - c, т.е. меньшую 1.
Но степень многочлена меньше 1 только в случае, когда она равна 0, и поэтому в обоих случаях r на самом деле является числом - нулем или отличным от нуля.
Подставив теперь в равенство f = (x - c)q + r значение x = c, мы получим
f(с) = (с - c)q(с) + r = 0,
так что действительно r = f(c), и первое утверждение доказано.
Теперь первое утверждение почти очевидно. В самом деле, утверждение "f делится на x - c" означает, что остаток от деления равен 0. Но остаток, по доказанному, равен f(c), так что "f делится на x - c" означает то же самое, что и f(c) = 0.
Теорема Безу дает возможность, найдя один корень многочлена, искать далее корни многочлена, степень которого на 1 меньше: если f(c) = 0, то f = (x - c)q, и остается решить уравнение q(x) = 0. Иногда этим приемом - он называется понижением степени - можно найти все корни многочлена. В частности, подобрав один корень кубического уравнения, можно его полностью решить - после понижения степени достаточно решить полученное квадратное уравнение.
Решим в качестве примера уравнение
x4 - x3 - 6x2 - x + 3 = 0.
Целые корни многочлена f = x4 - x3 - 6x2 - x + 3 должны быть делителями свободного члена, так что это могут быть только числа ±1 и ±3. При этом 1 не является корнем многочлена f, поскольку сумма его коэффициентов, очевидно, не равна 0.
При x = -1: имеем схему
|
1 |
-1 |
-6 |
-1 |
3 |
|
|
-1 |
1 |
-2 |
-4 |
3 |
0 |
Мы видим, что -1 - корень f , и в частном получается многочлен
g = x3 - 2x2 - 4x +3.
Значение x = 1 второй раз проверять незачем: если бы число 1 было корнем g, то оно было бы и корнем f, что неверно. А -1 проверить обязательно - ничто не мешает ей быть также и корнем частного g:
|
1 |
-2 |
-4 |
3 |
|
|
-1 |
1 |
-3 |
-1 |
4 |
Следовательно, g(-1) 0.
Составим схему Горнера для x = 3:
|
1 |
-2 |
-4 |
3 |
|
|
3 |
1 |
1 |
-1 |
0 |
Следовательно, g(3)
= 0, и при делении g
на x - 3 получается
многочлен x2-
x - 1, корни
которого (1± )/2.
)/2.
Таким образом, многочлен f,
а значит, и исходное уравнение имеет 4
корня: -1, 3 и (1± )/2.
)/2.
30. Следствия из теоремы Безу. Теорема Безу позволяет частично ответить и на важный теоретический вопрос - Сколько корней может иметь многочлен?
Теорема. Многочлен степени n имеет в любом поле не более n корней.
Доказательство. Пусть многочлен f степени n имеет k корней, и c -один из его корней. Предположим противное - пусть k>n.
По теореме Безу, f = (x - c)g, и частное g имеет степень n - 1. Всякий корень f, отличный от c, является одновременно и корнем g: если f(a) = 0, то (a - c)g(a) = 0, откуда g(a) = 0, так как a c. Другими словами, многочлен g имеет, по меньшей мере k - 1>n - 1 корень, т.е. число его корней также больше его степени.
Но с многочленом g можно провести те же рассуждения, и на втором шагу получить новый многочлен h, число корней которого также больше его степени. Продолжая таким же образом, мы придем к многочлену степени 2, имеющему больше 2 корней, чего не может быть.
Полученное противоречие показывает, что предположение k>n неверно, и следовательно, k не больше n, что и требовалось доказать.
Из теоремы о числе корней вытекают два исключительно важных и для теории, и для практики утверждения.
Следствие 1. Два многочлена степени, не большей n, принимают одинаковые значения при n + 1 значении x тогда и только тогда, когда при каждой степени x они имеют одинаковые коэффициенты.
Следствие 2. Два многочлена принимают одинаковые значения при всех значениях x тогда и только тогда, когда при каждой степени x они имеют одинаковые коэффициенты.
9. Разложение многочлена в произведение неприводимых
множителей и его единственность
10. Основная теорема арифметики кольца k[x]. Любой многочлен положительной степени можно разложить в произведение неприводимых сомножителей, и такое представление единственно с точностью до ассоциированности и порядка сомножителей.
Доказательство. 1. Существование. Индукцией по n докажем, что каждый многочлен f степени n 1 можно разложить в произведение неприводимых сомножителей. Основанием индукции при n = 1 служит тривиальное разложение f = f. Сделав индуктивное предположение, рассмотрим многочлен f степени n. Если f - неприводим, то разложение имеет вид: f = f; если же f - приводим, то его можно записать в виде f = gh, где степени g, h меньше степени f. По предположению индукции многочлены g и h можно разложить на неприводимые сомножители:
g = p>1>p>2 >. . . p>s>, h = q>1>q>2 >. . . q>t>,
поэтому
f = p>1>p>2 >. . . p>s>q>1>q>2 >. . . q>t>.
2. Единственность. Предположим, что некоторый многочлен f имеет два разложения на неприводимые сомножители:
f = p>1>p>2 >. . . p>s> , f = q>1>q>2 >. . . q>t>,
тогда
p>1>p>2 >. . . p>s >= q>1>q>2 >. . . q>t>.
Левая часть последнего равенства делится на p>1>, значит, правая часть также делится на p>1>. По основному свойству неприводимого многочлена на p>1> делится либо q>1>, либо q>2>, . . . , либо q>t>. Изменяя, если надо нумерацию сомножителей, можно считать, что p>1> делит q>1>, и поскольку q>1 >неприводим, то они ассоциированы, т.е. для некоторого числа c верно p>1 >= cq>1>. Значит, сокращая на p>1> обе части равенства
p>1>p>2 >. . . p>s >= p>1>q>2 >. . . q>t>,
получаем:
p>2 >. . . p>s >= (cq>2 >) . . . q>t>.
Обозначим данное произведение через m, и заметим, что deg m < deg f. По предположению индукции можно считать, что для m выполнено утверждение теоремы, т.е. левая часть последнего равенства отличается от правой либо перестановкой сомножителей, либо их ассоциированностью, значит, и в исходном равенстве
p>1>p>2 >. . . p>s >= q>1>q>2 >. . . q>t>
s = t и одна часть отличается от другой только порядком сомножителей и их ассоциированностью.
Пример. Разложить x6 - 1 на неприводимые множители над Q.
Решение. x6 - 1 = (x3 - 1)(x3 + 1) = (x - 1)( x2 + x + 1)(x + 1)( x2 - x + 1).
20. Каноническое разложение числа.
Обозначим через (k) - множество неприводимых нормированных многочленов над полем k.
Тогда произвольный многочлен f представим в виде произведения
c ,
где a>i >
0, p>i>
(k),
ck.
,
где a>i >
0, p>i>
(k),
ck.
Указанное разложение однозначно определяется многочленом f и называется его каноническим разложением; число a>i> называется показателем p>i >в каноническом разложении.
Канонические разложения удобны для доказательства различных свойств делимости и вычисления НОД и НОК. Приведем важнейшие из них.
10.
f :=
c делит
g :=
d
делит
g :=
d
a>1>
b>1>,
a>2>
b>2>,
. . . , a>n>
b>n>.
a>1>
b>1>,
a>2>
b>2>,
. . . , a>n>
b>n>.
Доказательство. Пусть g
= fh,
a>1>
> b>1>,
h := e .
Тогда b>1 >=
a>1>
+ c>1 >>
b>1>,
что невозможно. Обратное утверждение
очевидно.
.
Тогда b>1 >=
a>1>
+ c>1 >>
b>1>,
что невозможно. Обратное утверждение
очевидно.
20. Пусть имеются канонические разложения многочленов f и g:
f = c ,
g = d
,
g = d .
.
Тогда
НОД(f,
g) =
 ,
НОК(f, g)
=
,
НОК(f, g)
=
 ,
,
где c>i >= min (a>i>, b>i>), d>i >= max (a>i>, b>i>).
Доказательство. Пусть
=
 , где c>i >=
min (a>i>,
b>i>).
Тогда по свойству 10
многочлен
является делителем
многочленов f
и g и всякий
общий делитель f
и g делит
многочлен .
Следовательно,
= НОД(f,
g).
, где c>i >=
min (a>i>,
b>i>).
Тогда по свойству 10
многочлен
является делителем
многочленов f
и g и всякий
общий делитель f
и g делит
многочлен .
Следовательно,
= НОД(f,
g).
Аналогично доказывается и второе утверждение.
Из свойства 20 немедленно вытекает свойство
30. (Связь между НОД и НОК).
НОД(f, g) НОК(f, g) = f g.
10. Теорема о строении простого алгебраического расширения
10. Понятие минимального многочлена.
Пусть - алгебраическое число над полем k, т.е. корень ненулевого многочлена с коэффициентами из поля k.
Определение. Нормированный многочлен (, k, x) над полем k называется минимальным многочленом числа , если выполнены условия:
а) (x) - неприводим над полем k, т.е. не разлагается в произведение многочленов положительной степени с коэффициентами из k;
б) () = 0, т.е. - корень многочлена (x).
Примеры.
|
|
i |
|
|
i
+
|
|
(, Q, x) |
x2 + 1 |
x2 - 5 |
x2 + 2x - 1 |
x4 - 4x2 + 16 |
20. Основные свойства минимальных многочленов.
1. Если f(x) k[x] и f() = 0, то f(x) делится на минимальный многочлен (х) числа .
Доказательство. В самом деле, предположив, что f не делится на , запишем
f = g + r, deg r < deg
на основании теоремы о делении с остатком. Откуда r()=0. Поскольку многочлены r и взаимно просты, то у них не может быть общих корней - противоречие.
2. Допустим, что - алгебраическое число, а g(x) - нормированный многочлен наименьшей положительной степени такой, что g(x) k[x] и g() = 0. Тогда g(x) - минимальный многочлен числа .
Доказательство немедленно вытекает из свойства 1.
3. Минимальный многочлен алгебраического числа над данным полем определен однозначно.
Для доказательства достаточно применить свойство 2.
Определение. Степень минимального многочлена числа называется степенью числа ; обозначение deg >k> .
4. k deg> k> = 1.
Доказательство немедленно получается из определений.
5. Если - алгебраическое число степени n, то 1, , 2, ..., n-1 линейно независимы над полем k, т.е. (c>0>, c>1>, ..., c>n-1>> >k) c>0> + c>1> + ... + c>n-1>n-1 = 0 возможно только в случае c>0> = c>1> = . . . = c>n-1> = 0.
Доказательство. Действительно, если указанные степени числа линейно зависимы, то это число является корнем некоторого многочлена над k, степени меньшей чем .
6. Пусть
- алгебраическое число, f(x)
k[x]
и f()
0. Тогда дробь
 представима в виде
представима в виде
 =
g()
для некоторого g(x)
k[x].
=
g()
для некоторого g(x)
k[x].
Доказательство. В самом деле, многочлены f и взаимно просты (иначе f делился бы на ), значит, по теореме о линейном представлении НОД: для некоторых многочленов g и h над k верно равнство
fg + h = 1.
Откуда f() g() = 1, что и требовалось.
30. Строение простых алгебраических расширений.
Определение. Пусть k - подполе в L; L. Наименьшее подполе в L, содержащее число и подполе k, обозначаемое k(), называется простым расширением поля k (говорят также, что k() получено присоединением к полю k числа ).
Из приведенных свойств легко вывести теорему.
Теорема (о строении простого алгебраического расширения).
Для любого алгебраического числа над полем k линейное пространство k() обладает базисом из элементов вида
1, , 2, . . . , n-1, где n = deg>k >.
Доказательство. Легко понять, что k() состоит из дробей f()/g(), где f(x), g(x) - многочлены над полем k и g() 0. Обозначим через k[] - кольцо значений многочленов в точке , т.е. k[] = { f()f(x) k[x]}.
Из свойства 6 вытекает равенство k() = k[]. Из теоремы о делении с остатком следует, что значение произвольного многочлена над полем k в точке является линейной комбинацией над полем k указанных в теореме степеней элемента . Наконец, из свойства 5 следует линейная независимочть над полем k этих степеней.
40. Освобождение от иррациональности в знаменателе дроби.
Разберем различные способы решения задачи об освобождении от иррациональности в знаменателе дроби. Принципиальная возможность ее решения вытекает из теоремы о строении простого алгебраического расширения.
Пример 1. Освободиться от иррациональности в знаменателе дроби:
 .
.
Решение. Обозначим через c
число
 ,
и воспользуемся известной формулой
суммы членов геометрической прогрессии:
,
и воспользуемся известной формулой
суммы членов геометрической прогрессии:
1+ c + c2+ c3+ c4 = (c5 - 1)/(c - 1) = 1/(c - 1),
следовательно,
 .
.
Пример 2. Освободиться от иррациональности в знаменателе дроби:
 .
.
Решение. Обозначим через c
число
 ,
и запишем сначала дробь
,
и запишем сначала дробь

в виде суммы простейших:
 .
.
Теперь, используя схему Горнера, каждую из указанных дробей можно заменить на многочлен относительно c. Сначала разделим c5 - 2 на c + 1:
-
1
0
0
0
0
-2
-1
1
-1
1
-1
1
-3
следовательно,
 = c4
- c3
+ c2
- c + 1.
= c4
- c3
+ c2
- c + 1.
Теперь разделим c5 - 2 на c + 2:
-
1
0
0
0
0
-2
-2
1
-2
4
-8
16
-34
следовательно,
 =
c4
- 2c3
+ 4c2
- 8c + 16.
=
c4
- 2c3
+ 4c2
- 8c + 16.
Тогда получаем
 =
34(c4
- c3
+ c2
- c + 1) - 3(c4
- 2c3
+ 4c2
- 8c + 16) =
=
34(c4
- c3
+ c2
- c + 1) - 3(c4
- 2c3
+ 4c2
- 8c + 16) =
= 31c4 - 40c3 + 22c2 - 10c - 14,
т.е.
 .
.
Пример 3. Освободиться от иррациональности в знаменателе дроби:
 .
.
Решение. Обозначим через c
число
 .
Найдем линейное представление НОД
многочленов f(x)
= x3
- 2 и g(x)
= 1 + 2x - x2:
.
Найдем линейное представление НОД
многочленов f(x)
= x3
- 2 и g(x)
= 1 + 2x - x2:
f(x) = - g(x)(x + 2) + r(x), где r(x) = 5x
-5g(x) = r(x)(x - 2) - 5.
Из этих равенств, получаем линейное представление НОД f(x) и g(x):
f(x)(x - 2) + g(x)(x2 + 1) = 5.
Подставляя в последнее равенство вместо x число c, получим
 =
c2
+ 1,
=
c2
+ 1,
следовательно,
 =
= .
.
Пример 4. Освободиться от иррациональности в знаменателе дроби:
 .
.
Решение. Обозначим через c
число
 и
применим метод неопределенных
коэффициентов. По теореме о строении
простого алгебраического расширения
существуют рациональные числа x,
y, z
такие, что
и
применим метод неопределенных
коэффициентов. По теореме о строении
простого алгебраического расширения
существуют рациональные числа x,
y, z
такие, что
 = xc2
+ yc + z или 89 = (c2
+ 16c
- 11)(xc2
+ yc + z).
= xc2
+ yc + z или 89 = (c2
+ 16c
- 11)(xc2
+ yc + z).
Раскрывая скобки и используя равенство c3 = 2, получаем:
89 = (32x + 2y - 11z) + (2x - 11y + 16z)c + (-11x + 16y + z)c2.
Так как числа 1, c, c2 линейно независимы над Q имеем
32x + 2y - 11z = 89, 2x - 11y + 16z = 0,
-11x + 16y + z = 0.
Решением
последней системы является набор чисел
(3, 2, 1). Значит, получаем ответ:
 .
.

 -
1
-
1