История тригонометрии в формулах и аксиомах

Тригонометрические функции

Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников ( - треугольник, а - измеряю).

В данном случае измерение треугольников следует понимать как решение треугольников, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них. Большое количество практических задач, а также задач планиметрии, стереометрии, астрономии и других приводятся к задаче решения треугольников.

Возникновение тригонометрии связано с землемерением, астрономией и строительным делом.

Впервые способы решения треугольников, основанные на изависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н .э.) и Клавдием Птолемеем (2 в. н. э.). Пожднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями.

Значительный вклад в развитие тригонометрии внесли арабские ученые аль-Батани (850-929) и Абу-ль-Вефа Мухамед-бен Мухамед (940-998), который составил таблицы синусов и тангенсов через 10’ с точностью до 1/604. Теорему синусов уже знали индийский ученый Бхаскара (р. 1114, год смерти неизвестен) и азербайджанский астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Насиреддин Туси в своей работе «Трактат о полном четырехстороннике» изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину.

Теорему тангенсов доказал Региомонтан (латинизированное имя немецкого астронома и математика Иоганна Мюллера (1436-1476)). Региомонтан составил также плдробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе.

Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543) – творца гелиоцентрической системы мира, Тихо Браге (1546-1601) и Иогана Кеплера (1571-1630), а также в работах математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трем данным.

Долгое время тригонометрия носила чисто геометрический характер. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Постепенно тригонометрия органически вошла в математический анализ, механику, физику и технические дисциплины.

Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались и приобрели важное значение для всей математики.

Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII в. Леонардом Эйлером (1707-1783) членом Петербургской Академии наук.

Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.

Позднее часть тригонометрии, которая изучает свойства тригонометрических функций и зависимости между ними, начали называть гониометрией (в переводе – наука об измерении углов, от греч.  - угол, - измеряю). Термин гониометрия в последнее время практически не употребляется.

Изучение свойств тригонометрических функций и зависимостей между ними отнесено к школьному курсу алгебры, а решение треугольников – к курсу геометрии.

Тригонометрические функции острого угла

В



прямоугольном треугольнике, имеющем данный угол , отношения сторон не зависят от размеров треугольника. Рассмотрим два прямоугольных треугольника АВС и А>1>В>1>С>1> (рис.1), имеющих равные углы А=А>1> =. Из подобия этих треугольников имеем:

Если величину угла  измерить, то написанные равенства остаются справедливыми, а измениться

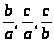
лишь числовое значение отношений и т.д. Поэтому отношения

м

В>1>

ожно рассматривать как функции угла .

В


а>1>

c>1>

c


С



а

90

90


С>1>

А

А>1>



b>1>

b


Рис.1.

Синусом острого угла называется отношение противоположного этому углукатета к гипотенузе. Обозначают это так:


sin=

Значения тригонометрических функций (отношений отрезков) являются отвлеченными числами.

Приближенные значения тригонометрических функций острого угла можно найти непосредственно согласно их определениям. Построив прямоугольный треугольник с острым углом a и измерив его стороны, согласно определениям мы можемвычислить значение, например, sina.

Пользуясь тем, что значения тригонометрических функций не зависят от размеров треугольника, для вычисления значений sin углов a=30; 45; 60 рассмотрим прямоугольный треугольник с углом a=30°; и катетом ВС=a=1, тогда гипотенуза этого треугольника с=2, а второй катет b=3; рассмотрим также треугольник с углом a=45 и катетом a=1, тогда для этого треугольника c=2 и b=1.

Полученные результаты запишем в таблицу.

30°

45°

60°

sina




Р
ис.2.

Приближенные значения тригонометрических функций для углов от 0 до 90 можно получить построив четверть круга, радиус которогопримем за 1, и его дугу разделимна 45 равных частей. Тогда градусная мера каждой части будет равна 2.

90 N

B 52


0,79

а

А b С 0,62 0 M Рис.3.

Радиусы АМ и АN разделим на 100 равных частей. Построим прямоугольный треугольник с вершиной в центре круга и катетом совпадающим с радиусом АМ и гипотенузой АВ=1. Если угол ВАС=, то по определению тригонометрических функций мы имеем:

sin=а

Для угла 52 на шкале радиуса АN находим, что а=0,79, а на шкале радиуса АМ находим, что b=0,62., то есть sin52=0,79.

Построив прямоугольные треугольники для углов =2, 4, 6, 8,…, 88, согласно рис.3., найдем значения (при аккуратных измерениях и вычислениях) с точностью до 0,01. Для углов 0 и 90 прямоугольных треугольников не существует. Однако, если гипотенуза АВ будет стремиться по положению к радиусу АМ, то угол 0, а катеты а0 и b1. В таком случае для полноты значений тригонометрических функций принимают, что

sin0=а=0; cos0=b=1.

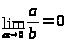
Что касается значений tg и ctg, то при 0 отношение ®0, т.е. , а отношение при a®0 неограниченно возрастает. Этот результат записывают как ®, где символ  указывает, что величина неограниченно возрастает и не может быть выражена никаким числом, так как знак ¥ не является каким-либо числом. Таким образом, принимают, что tg0=0, а ctg0 не существует, что чаще записывают как ctg0=¥.

Рассуждая аналогично при a®90 приходим к целесообразности принять что

sin90=1; cos90=0, tg90 не существует (tg90°®¥) и ctg90°=0.

Приведем таблицу значений синусов для углов от 0° до 90° с шагом 2°, которую можно получить указанным выше способом.

градусы

0

2

4

6

8

10

12

14

16

18

20

22

sin

0,00

0,03

0,07

0,10

0,14

0,17

0,21

0,24

0,28

0,31

0,34

0,37

градусы

24

26

28

30

32

34

36

38

40

42

44

46

sin

0,41

0,44

0,47

0,50

0,53

0,56

0,59

0,62

0,64

0,67

0,69

0,72

градусы

48

50

52

54

56

68

60

62

64

66

68

70

sin

0,74

0,77

0,79

0,81

0,83

0,93

0,87

0,88

0,90

0,91

0,93

0,94

градусы

72

74

76

78

80

82

84

86

88

90

sin

0,95

0,96

0,97

0,98

0,98

0,99

0,99

1,00

1,00

1,00

Пользуясь значениями тригонометрической функции y=sinx из таблицы, построим график.

y

y=sinx


1

0 30 60 90 x

Рис.4.

Основные соотношения между тригонометрическими функциями острого угла

Для прямоугольного треугольника в соответствии с теоремой Пифагора

a2+b2=c2

или

По определению тогда

(1)

Легко также найти следующие зависимости

(2)

(3)

(4)

(5)

Из соотношений (1)-(5), которые называют основными, можно вывести и другие вспомогательные соотношения, например:

(6)

(7)

(8)

Соотношения (1)-(8) связывают все тригонометрические ф
ункции так, что по значению одной из них для данного острого угла можно найти значения всех остальных функций для этого же угла.

Тригонометрические функции произвольного угла

Пусть в прямоугольной системе координат x0y задан радиус-вектор образующий с положительным направлением оси 0x угол . Будем считать, что ось 0x – начальная сторона, а вектор - конечная сторона угла . Проекция вектора на координатные оси соответственно обозначим a>x> и a>y>.

Можно показать, что отношения где а – длина вектора , зависят только от

величины угла  и не зависят от длины вектора . Поэтому эти отношения можно рассматривать как функции произвольного угла .

Синусом угла ,образованного осью 0x и произвольным радиусом-вектором , называется отношение проекции этого вектора на ось 0y к его длине:

y

A

a>y>


a>x> 0

x

Рис. 6.

Если не указано сколько оборотов совершил вектор вокруг точки 0, то положение вектора определяет угол с точностью до целого оборота, т.е углу с начальной стороной 0x и конечной стороной соответствует бесчисленное множество углов, которые выражаются формулой

360n+, где n=0; 1; 2; 3; 4; …

и sin(+360 n)=sin

Длина радиуса-вектора всегда число положительное. Проекция его на координатные оси величины алгебраические и в зависимости от координатных четвертей имеют следующие знаки:

В I четверти a>x>>0; a>y>>0;

Во II четверти a>x><0; a>y>>0;

В III четверти a>x><0; a>y> <0;

В IV четверти a>x>>0; a>y><0/

График функции y=sinx

До сих пор аргументами тригонометрических функций рассматривались именованные величины – углы (дуги), измеренные в градусах или радианах. Значения тригонометрических функций, как отношения отрезков, являются абстрактными величинами (числами). При изучении свойств тригонометрических функций приходится сравнивать изменения функции в связи с изменениями аргумента, а сравнивать можно только однородные или, что еще лучше, абстрактные величины.

Кроме того, введение тригонометрических функций от абстрактного аргумента дает возможность применять эти функции в различных вопросах математики, физики, техники и т.д.

В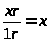место именованного значения аргумента тригонометрических функций в x (радианов) будем рассматривать абстрактное число где r обозначает радианы, ии по определению принять что

sinx, где x – абстрактное число, равен sinx, где x измерен в радианах.

Тригонометрические функции являются периодическими, то есть существует число а, отличное от 0, такое, что при любом целом nтождественно выполняется равенство:

f(x+na)=f(x), n=0; 1; 2 ...

Число а называется периодом функции. Период функции sinx равен 2. Для нее имеет место формула:

sin(x+2n)= sinx, где n=0; 1; 2 ...

График функции y=sinx называют синусоидой. Для построения графика можно взять значения аргумента x с определенным интервалом и составить таблицу значений y=sinx, соответствующих выбранным значениям x, а затем по точкам, как это часто делается в алгебре, построить график.

Строим в системе координат x>1>0>1>y>1> единичную окружность R=1 с центром 0>1> на оси абсцисс x>1>. Дугу этой окружности начиная от точки начиная от точки оси абсцисс x>1 >=+1, делим на n равных частей:

Затем строим вторую систему координат x0y, ось которой 0x совпадает с осью 0>1>> >x>1>> >, но сначало координат 0>1>(x>1 >=0) и 0(x=0) у етих систем различные. В новой системе координат отрезок оси абсцисс от x=0 до x=2 делим на n равных частей: Из точек деления окружности проводим прямые параллельные оси 0x, а из точек деления отрезка [0, 2] проводим прямые, перпендикулярные этой осм. Точки пересечения соответствующих прямых будут точками графика y=sinx, так как ординаты этихточек равны значениям синуса, соответствующим значениям аргумента в точках деления отрезка [0, 2].

Рис.8.

Некоторые свойства функции y=sinx

1. Непрерывность.

Функция y=sinx существует при всех действительных значения x, причем, график ее является сплошной кривой линией (без разрывов), т.е. функция sinx непрерывна.

2. Четность, нечетность.

Функция y=sinx нечетная и ее график симметричный относительно начала координат.

3. Наибольшие и наименьшие значения.

Все возможные значения функции sinx ограничены неравенствами

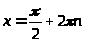-1 sinx +1,

причем sinx=+1, если

и sinx=-1, если

4.Нулевые значения (точки пересечения графика функции с осью абсцисс).

sinx=0, если x=n (n=0; 1; 2;…).

5. Интервалы возрастания и убывания.

Функция возрастает, т.е. большему значению аргумента соответствует большее значение функции на интервалах

(n=0; 1; 2;…).

И убывает, т.е. большему значению аргумента соответствует меньшее значение функции на интервалах

(n=0; 1; 2;…).