Дифференцированные уравнения

1.ВВЕДЕНИЕ

2.ОСНОВНЫЕ ПОНЯТИЯ

2.1.ЗАПИСЬ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

В СТАНДАРТНОЙ И ОПЕРАТОРНОЙ ФОРМЕ

В теории автоматического регулирования в настоящее время принято записывать дифференциальные уравнения в двух формах.

Первая форма записи. Дифференциальные уравнения записываются так, чтобы выходная величина и ее производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы, сама выходная величина находилась в уравнении с коэффициентом единица. Такое уравнение имеет вид:

= (1)

При такой записи коэффициенты k,k_>1>,...,k_>n> называют коэффициентами передачи, а T_>1>,...,T_>n> - постоянными времени данного звена.

Коэффициент передачи показывает отношение выходной величины звена к входной в установившемся режиме, т.е. определяет собой наклон линейной статической характеристики звена.

Размерности коэффициентов передачи определяются как

размерность k = размерность y(t) : размерность g(t)

размерность k1 = размерность y(t) : размерность g(t) (?)

Постоянными времени T_>1>,...,T_>n> имеют размерность времени.

Вторая форма записи. Считая условно оператор дифференцирования p= алгебраической величиной, произведем замену в уравнении (1):

= (2)

2.2. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЗВЕНА

Решим уравнение (2) относительно выходной величины y(t):

y(t)==

=W_>1>(s)+W_>2>(s)+...+W_>n>(s)

Здесь W_>1>(s),W_>2>(s),...,W_>n>(s) - передаточные функции.

При записи уравнений с изображениями выходной и входной величин по Лапласу передаточные функции сливаются в одну.

2.3. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ЗВЕНА

Динамические свойства звена могут быть определены по его переходной функции и функции веса.

Переходная функция h(t) представляет собой переходный процесс на выходе из звена, возникающий при подаче на его вход единичного ступенчатого воздействия - скачкообразного воздействия со скачком, равной единице.

Функция веса w(t) представляет собой реакцию на единичную импульсную функцию. Она может быть получена дифференцированием по времени переходной функции:

w(t)=

2.4.ЧАСТОТНАЯ ПЕРЕДАТОЧНАЯ ФУНКЦИЯ И ЧАСТОТНЫЕ

ХАРАКТЕРИСТИКИ

Важнейшей характкристикой динамического звена является его частотная передаточная функция. Ее можно получить с помощью передаточной фкнкции, заменив линейный оператор s на комплексный jw.

Так как передаточная функция есть отношение изображения по Лапласу выходной величины к входной, то при переходе от изображения Лапласа к изображению Фурье, мы получим, что частотная передаточная функция является изображением Фурье функции веса, то есть имеет место интегральное преобразование

W(j)=.

Частотная передаточная функция может быть представлена в следующем виде:

W(jw)=U(w)+jV(w)

где U(w) и V(w) - вещественная и мнимая части.

W(jw)=A(w),

где A(w) - модуль частотной передаточной функции, равный отношению амплитуде выходнгой величины к амплитуде входной,j(w) - аргументчастотной передаточной функции, равный сдвигу фаз выходной величины по отношению к входной.

Для наглядного представления частотных свойств звена используются так называемые частотные характеристики.

Амплитудная частотная характеристика (АЧХ) показывает, как пропускает звено сигнал различой частоты. Оценка пропускания делается по отношению амплитуд выходной и входной величин. То есть АЧХ - это модуль частотной передаточной функции:

A(w)=½W(jw)½

АЧХ строят для всео диапазона частот -¥<w<+¥, т.к. модуль частотной передаточной функции представляет собой четную функцию частоты.

Другой важной характеристикой является фазовая частотная характеристика (ФЧХ), которая находится как аргумент частотной передаточной функции:

j(w)=argW(jw)

4. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ

4.1. ПОЗИЦИОННЫЕ ЗВЕНЬЯ

Позиционные звенья - это такие звенья , в которых выходная и входная величины в установившемся режиме связаны линейной зависимостью y(t)=kg(t).Соответственно, переходная функция будет иметь вид W(s)=k, где N(s), L(s) - многочлены.

4.1.1.ИДЕАЛЬНОЕ УСИЛИТЕЛЬНОЕ ( БЕЗЫНЕРЦИОННОЕ ) ЗВЕНО

1. Данное звено описывается следующим уравнением:

a_>o>y(t)=b_>o>g(t) (1)

Коэффициенты имеют следующие значения:

a_>o>=2

b_>o>=4

Запишем это уравнение в стандартной форме. Для этого разделим (1) на a_>o>:

y(t)=g(t)

y(t)=kg(t) (2),

где k=-коэффициент передачи.

Запишем исходное уравнение в операторной форме, используя подстановку p= .Получим:

y(t)=kg(t) (3)

2. Получим передаточную функцию для идеального звена. Воспользуемся преобразованиями Лапласа:

y(t)=Y(s)

g(t)=G(s)

По определению передаточная функция находится как отношение выходного сигнала к входному. Тогда уравнение (2) будет иметь вид:

Y(s)=kG(s)

W(s)=k (4)

3. Найдем выражения для переходной функции и функции веса. По определению аналитическим выражением переходной функции является решение уравнения (2) при нулевых начальных условиях, т.е. g(t)=1. Тогда

h(t)=k1(t) (5)

Функцию веса можно получить дифференцированием переходной функции:

w(t)==kd(t) (6)

4. Построим графики переходной функции и функции веса. Подставляя исходные данные, вычислим коэффициент передачи и временные характеристики:

k=2

h(t)=2×1(t)

w(t)=2×d(t)

Переходная функция представляет собой ступенчатую функцию с шагом k=2, а функция веса - импульсную функцию, площадь которой равна k=2.

5. Получим частотную передаточную функцию, заменив в передаточной функции (4) s на jw:

W(s)=k

W(jw)=k (7)

W(jw)=U(w)+jV(w)

U(w)=k

V(w)=0

6. Получим аналитические выражения для частотных характеристик. По определению амплитудная частотная характеристика (АЧХ) - это модуль частотной передаточной функции, т.е.

A(w)=½W(jw)½

A(w)=k (8)

Фазовая частотная характеристика (ФЧХ) - это аргумент частотной передаточной функции, т.е.

j(w)=argW(jw)

j(w)=0 (9)

Для построения логарифмических частотных характеристик вычислим

L(w)=20lg A(w)

L(w)=20lgk

7. Построим графики частотных характеристик. Для этого сначала получим их численные значения.

k=2

A(w)=2

j(w)=0

L(w)=20lg2

U(w)=2

V(w)=0

Вывод: Примером рассмотренного звена может являться механический редуктор, делитель напряжения, индукционные датчики и т.д. Но беэынерционное звено является некоторой идеализацией реальных звеньев. В действительности ни одно звено не может равномерно пропускать все частоты от нуля до бесконечности. Обычно к такому виду сводится одно из реальных звеньев , рассмотренных ниже , если можно пренебречь влиянием динамических процессов.

4.1.2. УСИЛИТЕЛЬНОЕ ЗВЕНО С ЗАПАЗДЫВАНИЕМ

1. Данное звено описывается следующим уравнением:

a_>o>y(t)=b_>o>g(t-t) (1)

Коэффициенты имеют следующие значения:

a_>o>=2

b_>o>=4

t=0,1с

Запишем это уравнение в стандартной форме. Для этого разделим (1) на a_>o>:

y(t)= g(t-t)

y(t)=kg(t-t) (2),

где k=-коэффициент передачи.

Запишем исходное уравнение в операторной форме, используя подстановку p= .Получим:

y(t)=kg(t-t) (3)

2. Получим передаточную функцию для идеального звена. Воспользуемся преобразованиями Лапласа:

y(t)=Y(s)

g(t-t)=G(s)e^-^t^s

Y(s)=kG(s)e^-^t^s

W(s)= ke^-^t^s (4)

3. Найдем выражения для переходной функции и функции веса. ПО определению аналитическим выражением переходной функции является решение уравнения (2) при нулевых начальных условиях, т.е. g(t)=1.Тогда

h(t)=y(t)=k g(t-t)=k1(t) (5)

Функцию веса можно получить дифференцированием переходной функции:

w(t)==kd(t-t) (6)

k=2

h(t)=2×1(t-t)

w(t)=2×d(t-t)

Переходная функция представляет собой ступенчатую функцию с шагом k=2 и запаздыванием на t=0,1с, а функция веса - импульсную функцию с таким же запаздыванием, площадь которой равна k=2.

5. Получим частотную передаточную функцию, заменив в передаточной функции (4) s на jw:

W(s)=k e^-^t^s

W(jw)=k e^-j^wt =k(costw-jsintw) (7)

W(jw)=U(w)+jV(w)

U(w)=k costw

V(w)=-ksintw

A(w)=½W(jw)½

A(w)=k (8)

Фазовая частотная характеристика (ФЧХ) - это аргумент частотной передаточной функции, т.е.

j(w)=argW(jw)

j(w)= tw (9)

Для построения логарифмических частотных характеристик вычислим

L(w)=20lg A(w)

L(w)=20lgk

7. Построим графики частотных характеристик. Для этого сначала получим их численные значения.

k=2

A(w)=2

j(w)=0,1w

L(w)=20lg2

U(w)=2cos0,1w

V(w)=-2sin0,1w

Вывод:

4.1.3. УСТОЙЧИВОЕ АПЕРИОДИЧЕСКОЕ ЗВЕНО 1-го ПОРЯДКА

1. Данное звено описывается следующим уравнением:

a_>1> +_>>a_>o>y(t) =b_>o>g(t) (1)

Коэффициенты имеют следующие значения:

a_>1>=1,24_>>

a_>o>=2

b_>o>=4

Запишем это уравнение в стандартной форме. Для этого разделим (1) на ao:

+y(t)=g(t)

T_>1> +y(t)=kg(t) (2),

где k=-коэффициент передачи,

T_>1>=-постоянная времени.

Запишем исходное уравнение в операторной форме, используя подстановку p= .Получим:

(T_>1>p+1)y(t)=kg(t) (3)

2. Получим передаточную функцию для апериодического звена. Воспользуемся преобразованиями Лапласа:

y(t)=Y(s)

=sY(s)

g(t)=G(s)

T_>1>sY(s)+Y(s)=kG(s)

W(s)= (4)

h(t)=H(s)

H(s)=W(s)==

Переходя к оригиналу, получим

h(t)=k×1(t) (5)

Функцию веса можно получить дифференцированием переходной функции

w(t)=

или из преобразований Лапласа

w(t)=w(s)

w(s)=W(s)×1

W(s)==

Переходя к оригиналу, получим

w(t)= e ×1(t) (6)

4. Построим графики переходной функции и функции веса. Подставляя исходные данные, вычислим коэффициент передачи, постоянные времени и временные характеристики:

k=2

T_>1>=0.62

h(t)=2 ×1(t)

w(t)=3.2e×1(t)

Переходная функция представляет собой экспоненту. Множитель 1(t) указывает ,что экспонента рассматривается только для положительного времени t>0. Функция веса - также экспонента, но со скачком в точке t=0 на величину.

5. Получим частотную передаточную функцию, заменив в передаточной функции (4) s на jw:

W(s)=

W(jw)= (7)

W(jw)=U(w)+jV(w)==-j

U(w)=

V(w)=

A(w)=½W(jw)½

A(w)== (8)

Фазовая частотная характеристика (ФЧХ) - это аргумент частотной передаточной функции, т.е.

j(w)=argW(jw)

j(w)=arctgk - arctg

j(w)=-arctgT_>1> (9)

Для построения логарифмических частотных характеристик вычислим

L(w)=20lg A(w)

L(w)=20lg

7. Построим графики частотных характеристик. Для этого сначала получим их численные значения.

k=2

T_>1>=0.62

A(w)=

j(w)=arctg0.62w

L(w)=20lg

U(w)=

V(w)=

4.1.4. НЕУСТОЙЧИВОЕ АПЕРИОДИЧЕСКОЕ ЗВЕНО

1-го ПОРЯДКА

1. Данное звено описывается следующим уравнением:

a_>1> -_>>a_>o>y(t) =b_>o>g(t) (1)

Коэффициенты имеют следующие значения:

a_>1>=1,24_>>

a_>o>=2

b_>o>=4

Запишем это уравнение в стандартной форме. Для этого разделим (1) на ao:

-y(t)=g(t)

T_>> -y(t)=kg(t) (2),

где k=-коэффициент передачи,

T=-постоянная времени.

Запишем исходное уравнение в операторной форме, используя подстановку p= .Получим:

(T_>>p-1)y(t)=kg(t) (3)

2. Получим передаточную функцию для апериодического звена. Воспользуемся преобразованиями Лапласа:

y(t) = Y(s)

=sY(s)

g(t)=G(s)

T_>>sY(s)-Y(s)=kG(s)

W(s)= (4)

h(t)=H(s)

H(s)=W(s)==

Переходя к оригиналу, получим

h(t)=k×1(t) (5)

Функцию веса можно получить дифференцированием переходной функции

w(t)=

или из преобразований Лапласа

w(t)=w(s)

w(s)=W(s)×1

W(s)==

Переходя к оригиналу, получим

w(t)= e ×1(t) (6)

k=2

T_>>=0.62

h(t)=2 ×1(t)

w(t)=3.2e×1(t)

5. Получим частотную передаточную функцию, заменив в передаточной функции (4) s на jw:

W(s)=

W(jw)= (7)

W(jw)==j=U(w)+jV(w)

U(w)=

V(w)=

A(w)=½W(jw)½

A(w)== (8)

Фазовая частотная характеристика (ФЧХ) - это аргумент частотной передаточной функции, т.е.

j(w)=argW(jw)

j(w)=arctgk - arctg

j(w)=-arctg(-Tw) (9)

Для построения логарифмических частотных характеристик вычислим

L(w)=20lg A(w)

L(w)=20lg

7. Построим графики частотных характеристик. Для этого сначала получим их численные значения.

k=2

T_>>=0.62

A(w)=

j(w)=-arctg(-0.62w)

L(w)=20lg

U(w)=

V(w)=

4.1.5. АПЕРИОДИЧЕСКОЕ ЗВЕНО 2-го ПОРЯДКА

1. Данное звено описывается следующим уравнением:

a_>2>+a_>1> +_>>a_>o>y(t) =b_>o>g(t) (1)

Коэффициенты имеют следующие значения:

a_>2>=0,588

a_>1>=50,4

a_>o>=120

b_>o>=312

Запишем это уравнение в стандартной форме. Для этого разделим (1) на ao:

++y(t)=g(t)

+T_>1> +y(t)=kg(t) (2),

где k=-коэффициент передачи,

T_>1>=,T_>2>²=-постоянные времени.

Если корни характеристического уравнения для дифференциального уравнения 2-го порядка вещественны (это выполняется при T_>1>>2T_>2>), то оно является апериодическим 2-го порядка. Проверим это для нашего уравнения:

T_>1>=0,42

2T_>2>=0,14

0,42>014, следовательно, данное уравнение - апериодическое.

Запишем исходное уравнение в операторной форме, используя подстановку p= .Получим:

(p²+T_>1>p+1)y(t)=kg(t) (3)

2. Получим передаточную функцию для колебательного звена. Воспользуемся преобразованиями Лапласа:

y(t) = Y(s)

=sY(s)

=s²Y(s)

g(t)=G(s)

s²Y(s)+T_>1>sY(s)+Y(s)=kG(s)

W(s)= (4)

h(t)=H(s)

H(s)=W(s)== , где

T_>3,4>=

Разложив на элементарные дроби правую часть этого выражения, получим

H(s)=

Переходя к оригиналу, получим

h(t)=k×1(t) =

=k ×1(t)(5)

Функцию веса можно получить дифференцированием переходной функции

w(t)=

или из преобразований Лапласа

w(t)=w(s)

w(s)=W(s)×1==

Разложив на элементарные дроби правую часть этого выражения, получим

w(s)=

Переходя к оригиналу, получим

w(t)= =

= (6)

5. Получим частотную передаточную функцию, заменив в передаточной функции (4) s на jw:

W(s)=

W(jw)= (7)

Выделим вещественную и мнимую части :

W(jw) ==

U(w)=

V(w)=

A(w)=½W(jw)½

A(w)==..............(8)

Фазовая частотная характеристика (ФЧХ) - это аргумент частотной передаточной функции, т.е.

j(w)=argW(jw)

j(w)=................

j(w)=............... (9)

Для построения логарифмических частотных характеристик вычислим

L(w)=20lg A(w)

L(w)=...................

7. Построим графики частотных характеристик. Для этого сначала получим их численные значения.

4.1.6. КОЛЕБАТЕЛЬНОЕ (УСТОЙЧИВОЕ) ЗВЕНО

1. Данное звено описывается следующим уравнением:

a_>2>+a_>1> +_>>a_>o>y(t) =b_>o>g(t) (1)

Коэффициенты имеют следующие значения:

a_>2>=0,588

a_>1>=0,504

a_>o>=12

b_>o>=31,20

Запишем это уравнение в стандартной форме. Для этого разделим (1) на ao:

++y(t)=g(t)

+T_>1> +y(t)=kg(t) (2),

где k=-коэффициент передачи,

T_>1>=,T_>2>²=-постоянные времени.

Если корни характеристического уравнения для дифференциального уравнения 2-го порядка комплексные (это выполняется при T_>1><2T_>2>), то оно является колебательным. Проверим это для нашего уравнения:

T_>1>=0,042

2T_>2>=0,14

0,042<014, следовательно, данное уравнение - колебательное.

Представим данное уравнение в следующем виде:

пусть T_>2>=T, .

Тогда уравнение (2):

Здесь T - постоянная времени, x - декремент затухания (0<x<1).

Запишем исходное уравнение в операторной форме, используя подстановку p= .Получим:

(p²+2xTp+1)y(t)=kg(t) (3)

2. Получим передаточную функцию для колебательного звена. Воспользуемся преобразованиями Лапласа:

y(t) = Y(s)

=sY(s)

=s²Y(s)

g(t)=G(s)

s²Y(s)+2xT_>>sY(s)+Y(s)=kG(s)

W(s)= (4)

h(t)=H(s)

H(s)=W(s)=

Разложив на элементарные дроби правую часть этого выражения, получим

H(s)==

Заменим в этом выражении ,.Тогда

H(s)==

Переходя к оригиналу, получим

h(t)=k =

=k ×1(t) (5)

Функцию веса можно получить дифференцированием переходной функции

w(t)=

или из преобразований Лапласа

w(t)=w(s)

w(s)=W(s)×1===

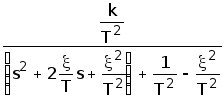Переходя к оригиналу, получим

w(t)= (6)

5. Получим частотную передаточную функцию, заменив в передаточной функции (4) s на jw:

W(s)=

W(jw)= (7)

Выделим вещественную и мнимую части :

W(jw)=

U(w)=

V(w)

A(w)=½W(jw)½

A(w)== (8)

Фазовая частотная характеристика (ФЧХ) - это аргумент частотной передаточной функции, т.е.

j(w)=argW(jw)

j(w)=argk - arg(2xTjw - T²w²+1)= - arctg

j(w)= - arctg (9)

Для построения логарифмических частотных характеристик вычислим

L(w)=20lg A(w)

L(w)=20lg

7. Построим графики частотных характеристик. Для этого сначала получим их численные значения.

4.1.6. КОЛЕБАТЕЛЬНОЕ (НЕУСТОЙЧИВОЕ) ЗВЕНО

1. Данное звено описывается следующим уравнением:

a_>2>- a_>1> +_>>a_>o>y(t) =b_>o>g(t) (1)

Коэффициенты имеют следующие значения:

a_>2>=0,588

a_>1>=0,504

a_>o>=12

b_>o>=31,20

Запишем это уравнение в стандартной форме. Для этого разделим (1) на ao:

- +y(t)=g(t)

-T_>1> +y(t)=kg(t) (2),

где k=-коэффициент передачи,

T_>1>=,T_>2>²=-постоянные времени.

T_>1>=0,042

2T_>2>=0,14

0,042<014, следовательно, данное уравнение - колебательное.

Представим данное уравнение в следующем виде:

пусть T_>2>=T, .

Тогда уравнение (2):

Здесь T - постоянная времени, x - декремент затухания (0<x<1).

Запишем исходное уравнение в операторной форме, используя подстановку p= .Получим:

(p²- 2xTp+1)y(t)=kg(t) (3)

2. Получим передаточную функцию для колебательного звена. Воспользуемся преобразованиями Лапласа:

y(t) = Y(s)

=sY(s)

=s²Y(s)

g(t)=G(s)

s²Y(s) - 2xT_>>sY(s)+Y(s)=kG(s)

W(s)= (4)

h(t)=H(s)

H(s)=W(s)=

Разложив на элементарные дроби правую часть этого выражения, получим

H(s)==

Заменим в этом выражении ,.Тогда

H(s)==

Переходя к оригиналу, получим

h(t)=k =

=k ×1(t) (5)

Функцию веса можно получить дифференцированием переходной функции

w(t)=

или из преобразований Лапласа

w(t)=w(s)

w(s)=W(s)×1===

Переходя к оригиналу, получим

w(t)= (6)

5. Получим частотную передаточную функцию, заменив в передаточной функции (4) s на jw:

W(s)=

W(jw)= (7)

Выделим вещественную и мнимую части :

W(jw)=

U(w)=

V(w)

A(w)=½W(jw)½

A(w)== (8)

Фазовая частотная характеристика (ФЧХ) - это аргумент частотной передаточной функции, т.е.

j(w)=argW(jw)

j(w)=argk - arg(1 - 2xTjw - T²w²)= - arctg

j(w)= - arctg (9)

Для построения логарифмических частотных характеристик вычислим

L(w)=20lg A(w)

L(w)=20lg

7. Построим графики частотных характеристик. Для этого сначала получим их численные значения.

4.1.5. КОЛЕБАТЕЛЬНОЕ КОНСЕРВАТИВНОЕ ЗВЕНО

1. Данное звено описывается следующим уравнением:

a_>2>+_>>a_>o>y(t) =b_>o>g(t) (1)

Коэффициенты имеют следующие значения:

a_>2>=0,0588

a_>o>=12

b_>o>=31,20

Запишем это уравнение в стандартной форме. Для этого разделим (1) на ao:

+y(t)=g(t)

+ y(t)=kg(t) (2),

где k=-коэффициент передачи,

T²=-постоянная времени.

Это уравнение является частным случаем колебательного уравнения при x=0.

Запишем исходное уравнение в операторной форме, используя подстановку p= .Получим:

(T²p²+1)y(t)=kg(t) (3)

2. Получим передаточную функцию для колебательного звена. Воспользуемся преобразованиями Лапласа:

y(t) = Y(s)

=s²Y(s)

g(t)=G(s)

T²s²Y(s)+Y(s)=kG(s)

W(s)= (4)

h(t)=H(s)

H(s)=W(s)=

Разложив на элементарные дроби правую часть этого выражения, получим

H(s)=

Заменим .Тогда

H(s)=

Переходя к оригиналу, получим

h(t)=k×1(t) (5)

Функцию веса можно получить из преобразований Лапласа

w(t)=w(s)

w(s)=W(s)×1===

Переходя к оригиналу, получим

w(t)= kw_>0>sinw_>0>t×1(t) (6)

5. Получим частотную передаточную функцию, заменив в передаточной функции (4) s на jw:

W(s)=

W(jw)= (7)

U(w)=

V(w)=0

A(w)=½W(jw)½

A(w)==(8)

Фазовая частотная характеристика (ФЧХ) - это аргумент частотной передаточной функции, т.е.

j(w)=argW(jw)

j(w)=argk - arg(1-T²w²)=0 (9)

Для построения логарифмических частотных характеристик вычислим

L(w)=20lg A(w)

L(w)=20lg (10)

7. Построим графики частотных характеристик. Для этого сначала получим их численные значения.

4.2. ИНТЕГРИРУЮЩИЕ ЗВЕНЬЯ

4.2.1. ИНТЕГРИРУЮЩЕЕ ИДЕАЛЬНОЕ ЗВЕНО

1. Данное звено описывается следующим уравнением:

a_>1> =b_>o>g(t) (1)

Коэффициенты имеют следующие значения:

a_>1>=1,24_>>

b_>o>=4

Запишем это уравнение в стандартной форме. Для этого разделим (1) на a_>1>:

=g(t)

_>> =kg(t) (2),

где k=-коэффициент передачи.

Запишем исходное уравнение в операторной форме, используя подстановку p= .Получим:

py(t)=kg(t) (3)

2. Получим передаточную функцию для данного звена. Воспользуемся преобразованиями Лапласа:

y(t)=Y(s)

=sY(s)

g(t)=G(s)

_>>sY(s)=kG(s)

W(s)= (4)

h(t)=H(s)

H(s)=W(s)=

Переходя к оригиналу, получим

h(t)=kt×1(t) (5)

Функцию веса можно получить дифференцированием переходной функции

w(t)=

w(t)==k×1(t) (6)

5. Получим частотную передаточную функцию, заменив в передаточной функции (4) s на jw:

W(s)=

W(jw)= (7)

W(jw)=

U(w)=0

V(w)=

A(w)=½W(jw)½

A(w)== (8)

Фазовая частотная характеристика (ФЧХ) - это аргумент частотной передаточной функции, т.е.

j(w)=argW(jw)

j(w)=argk - argjw

j(w)= - arctgw (9)

Для построения логарифмических частотных характеристик вычислим

L(w)=20lg A(w)

L(w)=20lg

7. Построим графики частотных характеристик.Для этого сначала получим их численные значения.

4.2.2. ИНТЕГРИРУЮЩЕЕ ИНЕРЦИОННОЕ ЗВЕНО

1. Данное звено описывается следующим уравнением:

+_>>a_>1> =b_>o>g(t) (1)

Коэффициенты имеют следующие значения:

a_>2>=0,0588_>>

a_>1>=0,504

b_>o>=31,20

Запишем это уравнение в стандартной форме. Для этого разделим (1) на a_>1>:

+ =g(t)

T+=kg(t) (2),

где k=-коэффициент передачи,

T=-постоянная времени.

Запишем исходное уравнение в операторной форме, используя подстановку p= .Получим:

(Tp²+p)y(t)=kg(t) (3)

2. Получим передаточную функцию для апериодического звена. Воспользуемся преобразованиями Лапласа:

y(t)=Y(s)

=sY(s)

=s²Y(s)

g(t)=G(s)

Ts²Y(s)+sY(s)=kG(s)

W(s)= (4)

h(t)=H(s)

H(s)=W(s)=

Разложив на элементарные дроби правую часть этого выражения, получим

H(s)=

Переходя к оригиналу, получим

h(t)= - kT×1(t)+kt×1(t)+kT×1(t)=

= (5)

Функцию веса можно получить из преобразований Лапласа

w(t)=w(s)

w(s)=W(s)×1=

Разложив на элементарные дроби правую часть этого выражения, получим

w(s)=

Переходя к оригиналу, получим

w(t)=k×1(t) (6)

5. Получим частотную передаточную функцию, заменив в передаточной функции (4) s на jw:

W(s)=

W(jw)= (7)

W(jw)

U(w)=

V(w)=

A(w)=½W(jw)½

A(w)== (8)

Фазовая частотная характеристика (ФЧХ) - это аргумент частотной передаточной функции, т.е.

j(w)=argW(jw)

j(w)=argk - argjw - arg

j(w)= - arctgw - arctgTw (9)

Для построения логарифмических частотных характеристик вычислим

L(w)=20lg A(w)

L(w)=20lg

7. Построим графики частотных характеристик.Для этого сначала получим их численные значения.

4.2.3. ИЗОДРОМНОЕ ЗВЕНО

1. Данное звено описывается следующим уравнением:

a_>1> =b_>1>+b_>o>g(t) (1)

Коэффициенты имеют следующие значения:

a_>1>=1,24_>>

b_>o>=4

b_>1>=4

Запишем это уравнение в стандартной форме. Для этого разделим (1) на a_>1>:

=+g(t)

=k_>1>+kg(t) (2),

где k_>1>=, k=-коэффициент передачи.

Запишем исходное уравнение в операторной форме, используя подстановку p= .Получим:

py(t)=(k_>1>p+k)g(t) (3)

2. Получим передаточную функцию для апериодического звена. Воспользуемся преобразованиями Лапласа:

y(t)=Y(s)

=sY(s)

g(t)=G(s)

=sG(t)

sY(s)=k_>1>sG(s)+kG(s)

W(s)= (4)

h(t)=H(s)

H(s)=W(s) =

Переходя к оригиналу, получим

h(t)= × 1(t) (5)

Функцию веса можно получить из преобразований Лапласа

w(t)=w(s)

w(s)=W(s)×1

W(s)=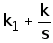

Переходя к оригиналу, получим

w(t)= k_>1>×d(t)+k×1(t) (6)

5. Получим частотную передаточную функцию, заменив в передаточной функции (4) s на jw:

W(s)=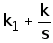

W(jw)= (7)

U(w)=k_>1>

V(w)=

A(w)=½W(jw)½

A(w)=............(8)

Фазовая частотная характеристика (ФЧХ) - это аргумент частотной передаточной функции, т.е.

j(w)=argW(jw)

j(w)=............

j(w)=............ (9)

Для построения логарифмических частотных характеристик вычислим

L(w)=20lg A(w)

L(w)=20lg........

7. Построим графики частотных характеристик.Для этого сначала получим их численные значения.

4.3.1.ДИФФЕРЕНЦИРУЮЩЕЕ ИДЕАЛЬНОЕ ЗВЕНО

1. Данное звено описывается следующим уравнением:

a_>o>y(t)=b_>1> (1)

Коэффициенты имеют следующие значения:

a_>o>=2

b_>1>=4

Запишем это уравнение в стандартной форме. Для этого разделим (1) на a_>o>:

y(t)=

y(t)=k (2),

где k=-коэффициент передачи.

Запишем исходное уравнение в операторной форме, используя подстановку p= .Получим:

y(t)=kpg(t) (3)

2. Получим передаточную функцию для идеального звена. Воспользуемся преобразованиями Лапласа:

y(t)=Y(s)

g(t)=G(s)

=sG(s)

Y(s)=ksG(s)

W(s)=ks (4)

3. Найдем выражения для переходной функции и функции веса из преобразлваний Лапласа,т.е.

h(t)=H(s)

H(s)=W(s)=k

Переходя к оригиналу, получим

h(t)=k×d(t) (5)

Функцию веса можно получить по преобразованию Лапласа из передаточной функции:

w(t)=w(s)

w(s)=W(s)×1=ks

Переходя к оригиналу, получим

w(t)=k (6)

5. Получим частотную передаточную функцию, заменив в передаточной функции (4) s на jw:

W(s)=ks

W(jw)=jkw (7)

W(jw)=U(w)+jV(w)

U(w)=0

V(w)=kw

A(w)=½W(jw)½

A(w)=k½w½ (8)

Фазовая частотная характеристика (ФЧХ) - это аргумент частотной передаточной функции, т.е.

j(w)=argW(jw)

j(w)=arctgkw (9)

Для построения логарифмических частотных характеристик вычислим

L(w)=20lg A(w)

L(w)=20lgk½w½

7. Построим графики частотных характеристик. Для этого сначала получим их численные выражения.

4.3.2.ДИФФЕРЕНЦИРУЮЩЕЕ РЕАЛЬНОЕ ЗВЕНО

1. Данное звено описывается следующим уравнением:

a_>1> +_>>a_>o>y(t) =b_>1> (1)

Коэффициенты имеют следующие значения:

a_>1>=1,24_>>

a_>o>=2

b_>1>=4

Запишем это уравнение в стандартной форме. Для этого разделим (1) на a_>1>:

+y(t)=

T+y(t)=k (2),

где k=-коэффициент передачи,

T_>1>=-постоянная времени.

Запишем исходное уравнение в операторной форме, используя подстановку p= .Получим:

(Tp+1)y(t)=kpg(t) (3)

2. Получим передаточную функцию для апериодического звена. Воспользуемся преобразованиями Лапласа:

y(t)=Y(s)

=sY(s)

g(t)=G(s)

=sG(s)

TsY(s)+Y(s)=ksG(s)

W(s)= (4)

h(t)=H(s)

H(s)=W(s)==

Переходя к оригиналу, получим

h(t)=×1(t) (5)

Функцию веса можно получить из преобразований Лапласа

w(t)=w(s)

w(s)=W(s)×1

W(s)= =

Переходя к оригиналу, получим

w(t)=×d(t) e ×1(t) (6)

5. Получим частотную передаточную функцию, заменив в передаточной функции (4) s на jw:

W(s)=

W(jw)=

W(jw)==

6.Найдем АЧХ:

A(w)=½W(jw)½

A(w)==

Найдем ФЧХ:

j(w)=argW(jw)

j(w)=arctgkw-arctgTw

L(w)=20lgA(w)

L(w)=20lg

4.3.3.ФОРСИРУЮЩЕЕ ЗВЕНО 1-го ПОРЯДКА

Данное звено описывается следующим уравнением:

a0y(t)=b1+b0g(t)

y(t)=+g(t)

k1=

y(t)=k1pg(t)+kg(t)

y(t)=Y(s)

g(t)=G(s)

Y(s)=k1sG(s)+kG(s)

W(s)=k1s+k

H(s)==k1+

h(t)=k1d(t)+k1(t)

W(jw)=k1jw+k

U(w)=k

V(w)=k1w

A(w)=½W(jw)½

A(w)=

j(w)=argW(jw)

j(w)=arctg

L(w)=20lgA(w)

L(w)=20lg

4.3.4.ФОРСИРУЮЩЕЕ ЗВЕНО 2-го ПОРЯДКА

a0y(t)=b2+b1+b0g(t)

y(t)=++g(t)

y(t)=k2+k1+kg(t)

y(t)=k2p2g(t)+k1pg(t)+kg(t)

Y(s)=(k2s2+k1s+k)G(s)

W(s)=k2s2+k1s+k

H(s)=k2s+k1+

h(t)=k2+k1d(t)+k11(t)

w(s)=W(s)=k2s2+k1s+k

w(t)=k2+k1+kd(t)

W(jw)=k1jw+k - k2w2

U(w)=k - k2w2

V(w)=k1jw

A(w)=

j(w)=arctg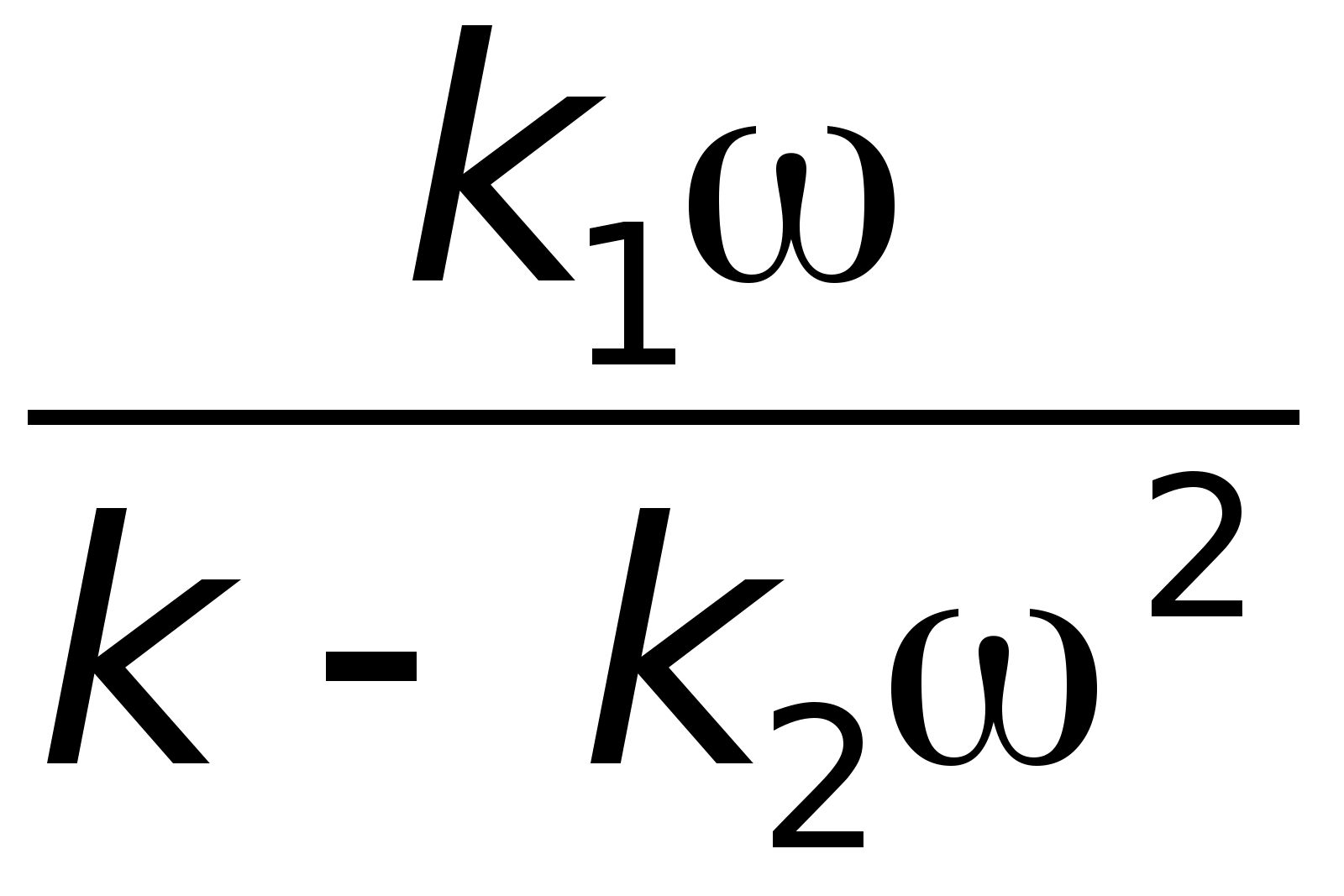

L(w)=20lg