Атомические разложения функций в пространстве Харди
Міністерство Освіти України
Одеський державний університет
ім. І.І.Мечнікова
Інститут математики, економіки та механіки
Атомічні розкладення функцій
у просторі Харді
Дипломна робота
студентки V курсу
факультету математики
Семенцовой В.А.
Науковий керівник
Вартанян Г.М.
Одеса - 2000
Содержание
Введение.................................................................................... 3
Глава I. Основные сведения об интеграле Пуассона и
пространствах
,
и
.................................
8
§I.1. Интеграл Пуассона..................................................... 8
§I.2.
Пространства
.......................................................
12
§I.3.
Пространства
и
.........................................
17
§I.4. Произведение Бляшке, нетангенциальная
максимальная функция............................................... 22
Глава II. Атомические разложения функции в пространстве
,
пространство ВМО........................................
26
§II.1.
Пространство
,
критерий принадлежности
функции из
пространству
.......................
26
§II.2.
Линейные ограниченные функционалы
на
,
двойственность
и ВМО.................................. 32
Литература.................................................................................. 37
Введение.
Целью настоящей работы является
изучение основных понятий и результатов,
полученных в области пространств Харди,
которая не изучалась в рамках
университетского курса. В работе
прослежена взаимосвязь между следующими
понятиями : интеграл Пуассона, пространства
,
,
и
,
раскрыта суть и структура этих объектов.
Описание указанных понятий вводится
именно в такой последовательности , так
как определение каждого последующего
объекта дается на основе понятий,
расположенных левее в выше перечисленном
ряду объектов.
Работа состоит из двух глав,
каждая из которых делится на параграфы.
В первой главе изучены свойства
пространств
,
,
,
а во второй мы доказываем коитерий
принадлежности функции из
пространству
и двойственность пространств
и
.
В работе мы рассматриваем случай
периодических
функций. Используемые обозначения имеют
следующий смысл:
- пространство
периодических,
непрерывных на
функций;
-
пространство
периодических,
бесконечно дифференцируемых на
функций;
- пространство
периодических,
суммируемых в степени р на
функций,
т.е.для которых
,
;
-
пространство
периодических
ограниченных на
функций;
-
носитель функции
.
В §I.1.вводится
понятие интеграла Пуассона: интегралом
Пуассона суммируемой на [-,]
2-периодической
комплекснозначной функции
называется функция
>r>
( x ) =
,
где
, t
-
ядро Пуассона.
Здесь мы доказываем следующие свойства ядра Пуассона, которые мы неоднократно будем использовать в ряде доказательств:
а)
;
б)
;
в) для любого >0
Основной целью данного
параграфа являются две теоремы о
поведении интеграла Пуассона
при
:
Теорема 1.
Для
произвольной (комплекснозначной) функции
(
-,
) , 1
p <
, имеет место равенство
;
если же (x) непрерывна на [ -, ] и (-) = () , то
.
Теорема 2 (Фату).
Пусть
-
комплекснозначная функция из
. Тогда
для п.в.
.
В этом параграфе мы обращались к следующим понятиям:
Определение1. Функция
называется
аналитической в точке
,
если она дифференцируема в этой точке
и в некоторой ее окрестности. Говорят,
что функция
аналитична
на некотором множестве,если она аналитична
в каждой точке этого множества.
Определение2.
Действительная функция двух действительных
переменных
называется гармонической в области
,
если
и удовлетворяет уравнению Лапласа:
.
Определение3. Две гармонические
функции
и
,
связанные условиями
Коши-Римана :
,
, называются гармонически сопряженными
функциями.
Определение4. Под нормой
пространства
понимается
,
.
Определение5. Под нормой
пространства
понимается
,
.
Определение6. Пусть
( или
,).
Модуль непрерывности ( соответственно
интегральный модуль непрерывности)
функции
определяется равенством
,
.
(
,
).
Определение7. Последовательность
функций,
определенных на множестве Х с заданной
на нем мерой, называется сходящейся
почти всюду к функции
,
если
для почти всех
,
т.е. множество тех точек
,
в которых данное соотношение не
выполняется, имеет меру нуль.
В §I.2
мы рассматриваем пространства
- это совокупность аналитических в
единичном круге функций F
(z) , для которых конечна
норма
.
Основным
результатом этого параграфа является
теорема о том, что любую функцию
(
)
можно предсавить в виде
,
,
,
где
для п.в.
, при этом
;
.
Использованные в данном параграфе понятия мы принимаем в следующих определениях:
Определение8. Говорят, что
действительная функция
,
заданная на отрезке [a,b],
имеет ограниченную вариацию, если
существует такая постоянная
,
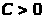что каково бы ни было разбиение отрезка
[a,b]
точками
выполнено неравенство
.
Определение9. Действительная
функция
,
заданная на отрезке [a,b],
называется абсолютно непрерывной на
[a,b], если для любого
найдется число
такое,
что какова бы ни была система попарно
непересекающихся интервалов
,
с суммой длин, меньшей
:
,
выполняется неравенство
.
В третьем параграфе первой главы
мы переходим к рассмотрению пространств
и
.
Пространство
()
представляет собой совокупность тех
функций
,
,
которые являются граничными значениями
функций (действительных частей функций)
из,
т.е. представимы в виде
(
).
Здесь мы получаем следующие результаты:
при
пространство
совпадает с
,
а при р=1
уже, чем
,
и состоит из функций
,
для которых и
.
В §I.4
мы вводим понятие произведения Бляшке
функции
,
аналитической в круге
с нулями
,
(
)
с учетом их кратности:
,
где
- кратность нуля функции
при
.
Здесь доказывается, что каждая
функция
представима в виде
,
где
не имеет нулей в круге
и
,
,а
- произведение Бляшке функции
.
Затем мы рассматриваем понятие
нетангенциальной максимальной функции
. Пусть
,
,
- произвольное число. Обозначим через
,
,
область, ограниченную двумя касательными,
проведенными из точки
к окружности
,
и наибольшей из дуг окружности, заключенных
между точками касания ( при
вырождается в радиус единичного круга).
Для
положим
,
,
где
- интеграл Пуассона функции
.
Функция
называется нетангенциальной максимальной
функцией для
.
Тут же мы доказываем теорему об
оценке
:
если
(),
,
то
и
.
Первые результаты о максимальных функциях были получены в 1930 году Харди и Литтлвудом.
Во второй главе два параграфа.
В
§II.1
рассматривается пространство
.
Как ранее отмечалось, оно уже, чем
.
Поэтому в данном параграфе большой
интерес представляет теорема - критерий
принадлежности функции пространству
.
Здесь вводится понятие атома:
действительная функция
называется атомом, если существует
обобщенный интервал
такой, что
а)
;
б)
;
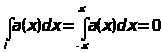в)
.
Атомом
назовем также функцию
,
.
Под обобщенным интервалом понимается
либо интервал из
,
либо множество вида
(
).
Данный параграф посвящен аналогу
теоремы, доказанной в 1974 году Р.Койфманом
о том, что функция
тогда
и только тогда, когда функция
допускает представление в виде
,
,
где
,
,
- атомы. (*)
При
этом
,
где inf
берется по всем разложениям вида (*)
функции
,
а с и С
- абсолютные константы.
Роль атомических разложений заключается в том, что они в ряде случаев позволяют свести вывод глубоких фактов к относительно простым действиям с атомами.
В
частночти, из атомического разложения
функций, принадлежащих пространству
,
легко вытекает полученный в 1971 году
Ч.Фефферманом результат о двойственности
пространств
и
.
Доказательству этого факта и посвящен
второй параграф данной главы. Сперва
мы вводим определение
:
пространство ВМО есть совокупность
всех функций
,
удовлетворяющих условию
, (91)
где
, а sup берется по
всем обобщенным интервалам
. А затем доказываем теорему о том, что
.
Глава I.
Основные сведения об интеграле Пуассона и
пространствах
,
и
§I.1.Интеграл Пуассона.
Пусть x , g(x) , xR1 –суммируемые на -, , 2- периодические, комплекснозначные функции. Через fg(x) будем обозначать свертку
fg(x)
=
dt
Из теоремы Фубини следует, что свертка суммируемых функций также суммируема на -, и
c>n >( fg ) = c>n> ( f ) c>-n> ( g ) , n = 0, 1 , 2 , ... ( 1 )
где c>n> ( f ) - коэффициенты Фурье функции f ( x ) :
c>n>
(f)=
-i
n tdt
, n = 0,
Пусть L1 (-) . Рассмотрим при r функцию
>r>
( x ) =
>n>
( f ) rn
ei n x
, x
. ( 2 )
Так как
для любых x ,
n = 0, ,
а ряд
сходится (так как согласно теореме
Мерсера [4] коэффициенты Фурье любой
суммируемой функции по ортогональной
системе ограниченных в совокупности
функций
стремятся к нулю при
),
то по признаку Вейерштрасса
ряд в правой части равенства (2) сходится
равномерно по х для любого фиксированного
r ,
r
. Коэффициенты
Фурье функции
>r>
х
равны c>n>
( f>r>
) = c>n>
(f)
r
n
, n = 0 , ,
а это значит, что >r
>
x
можно представить в виде свертки :
>r>
( x ) =
, ( 3 )
где
, t
( 4 )
Функция двух переменных Р>r> (t) , 0 r , t , называется ядром Пуассона , а интеграл (3) - интегралом Пуассона .
Следовательно,
P>r>
( t ) =
, 0r
, t
. ( 5 )
Если L ( - ) действительная функция , то , учитывая , что
c>-n
>( f ) =
,
n = 0
из соотношения (2) мы
получим :
f>r>
( x ) =
=
,
( 6 )
где
F ( z ) = c>0>
( f ) + 2
( z = reix
)
( 7 )
аналитическая в единичном круге функция как сумма равномерно сходящегося по х ряда [5]. Равенство (6) показывает, что для любой действительной функции L1( -, ) интегралом Пуассона (3) определяется гармоническая в единичном круге функция
u ( z ) = >r> (eix ) , z = reix , 0 r 1 , x [ -, ] .
При этом гармонически сопряженная с u (z) функция v (z) c v (0) = 0 задается формулой
v (z) = Im F (z) =
. ( 8 )
Утверждение1.
Пусть u (z) - гармоническая ( или аналитическая ) в круге z функция и (x) = u (eix) , x, . Тогда
u (z) =
( z = reix
,
z
) ( 10 )
Так как ядро Пуассона P>r> (t) - действительная функция, то равенство (10) достаточно проверить в случае, когда u (z) - аналитическая функция:
=
,
z
+
.
Но
тогда коэффициенты Фурье функции
связаны
с коэффициентами Фурье
функции
следующим образом :
и равенство (10) сразу следует из (2) и (3).
Прежде чем перейти к изучению поведения функции >r >(x) при r , отметим некоторые свойства ядра Пуассона:
а)
;
б)
;
(11)
в) для любого >0
Соотношения
а) и в) сразу следуют из формулы (5), а для
доказательства б) достаточно положить
в (2) и (3)
х
.
Теорема 1.
Для
произвольной (комплекснозначной) функции
(
-,
) , 1
p <
, имеет место равенство
;
если же (x) непрерывна на [ -, ] и (-) = () , то
.
Доказательство.
В силу (3) и свойства б) ядра Пуассона
.
( 12 )
Для
любой функции
, пользуясь неравенством Гельдера и
положительностью ядра Пуассона , находим
.
Следовательно,
.
Для
данного
найдем
=
()
такое, что
.
Тогда для r
, достаточно близких к единице, из
свойств а)-в) мы получим оценку
.
Аналогично, второе утверждение теоремы 1 вытекает из неравенства
.
Теорема 1 доказана.
Дадим определения понятий "максимальная функция" и "оператор слабого типа", которые понадобятся нам в ходе доказательства следующей теоремы.
ОпределениеI.1.
Пусть
функция
,
суммируема на любом интервале (a,b),
a<b,
.
Максимальной функцией
для функции
называется функция
,
где супремум берется по всем интервалам I , содержащим точку х.
Определение I.2.
Оператор
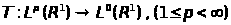называется оператором
слабого типа (р,р) , если
для любого y > 0
,
.
Теорема 2 (Фату).
Пусть
-
комплекснозначная функция из
. Тогда
для п.в.
.
Доказательство.
Покажем,
что для
и
, ( 13 )
где С - абсолютная константа , а M ( f, x ) - максимальная функция для f (x)*). Для этой цели используем легко выводимую из (5) оценку
(К - абсолютная константа).
Пусть
-
такое число, что
.
Тогда
для
.
Неравенство
(13) доказано. Возьмем
слабый тип (1,1) оператора
.
Используя его, найдем такую последовательность
функций
,что
,
( 14 )
для п.в.
.
Согласно (13) при x (-)
Учитывая
, что по теореме 1
для каждого x
[-
]
и (14)
из последней оценки получим
при r1.
Теорема 2 доказана.
Замечание1.
Используя
вместо (13) более сильное неравенство
(59), которое мы докажем позже, можно
показать, что для п.в. x
[-
]
,
когда точка reit
стремится к eix
по
некасательному к окружности
пути.
§I.2.Пространства
Hp.
Определение I.3.
Пространство
-
совокупность аналитических в единичном
круге функций F
(z) , для которых конечна
норма
. (15)
Пусть
комплекснозначная функция
удовлетворяет условиям
(16)
тогда функция F (z) , определенная равенством
(17)
принадлежит
пространству
,
причем
. (18)
Действительно,
аналитичность функции F
(z) следует из (16) и равенства
(2). Кроме того, в силу неравенства
мы имеем
()
С другой стороны , по теореме 1 ( а при р= в силу теоремы 2)
. Отсюда
()
Учитывая () и () , получим (18).
Ниже
мы докажем, что любую функцию
можно представить в виде (17). Для этого
нам потребуется
Теорема 3.
Пусть комплекснозначная функция (t) имеет ограниченную вариацию на [ -] и
(19)
Тогда (t) абсолютно непрерывна на [-].
Замечание2.
В (19) и ниже рассматривается интеграл Лебега-Стилтьеса, построенный по комплекснозначной функции ограниченной вариации (t) . Мы говорим, что
(t)= u (t)+ i v (t) имеет ограниченную вариацию (абсолютно непрерывна), если обе действительные функции u (t) и v (t) имеют ограниченную вариацию (соответственно абсолютно непрерывны). При этом интеграл
определен для каждой непрерывной на [-] функции f (t) , а также если
- характеристическая функция
замкнутого множества
.
Доказательство теоремы 3.
Нам
достаточно проверить, что для любого
замкнутого множества
,
,
(20)
Для этой цели убедимся, что справедлива
Лемма 1.
Пусть
F -
замкнутое, а V
- открытое множества , причем
и
.
Тогда для всякого
, существует функция
вида
, (21)
обладающая свойствами:
а)
;
б)
; (22)
в)
.
Выведем из леммы 1 оценку (20), а затем докажем саму лемму 1.
Пусть
, где
- конечная или бесконечная последовательность
дополнительных интервалов множества
F,
и для
.
Очевидно,
что
-
открытое множество и
.
Рассмотрим
для данных
функцию
,
построенную в лемме 1 для числа
и множества
.
Тогда нетрудно проверить[3],
что если
,
а
, то разность
.
(23)
Но в силу (19) и равномерной сходимости ряда (21) (так как ряд Фурье бесконечно дифференцируемой функции сходится равномерно)
,
и мы получаем равенство (20).
Перейдем к доказательству леммы 1. Нам понадобится
ОпределениеI.4.
Средние Фейера - это средние вида
,
где
,
,
- ядро Дирихле,
,
-
ядро Фейера.
Отметим,
что при
ядро Фейера обладает следующими
свойствами: а)
,
;
б)
,
Мз
которых вытекает, что для
и
,
Также
известно [3],
что средние Фейера
равномерно сходятся к
.
Пусть f(t) - непрерывная на [-, ] функция, для которой
и
Так
как средние Фейера
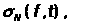равномерно
сходятся к
и
, то существует тригонометрический
полином
(24)
такой, что
(25)
Пусть
.
Рассмотрим для каждого
такую функцию
,
что
,
(функцию
можно построить следующим образом:
взять замкнутое множество
с мерой
, достаточно близкой к 2,
и положить
).
Так
как
(здесь число m
то же, что в (24)), то для достаточно
малых
функция
удовлетворяет соотношениям
(26)
При
этом
,
если
.
Тогда средние Фейера
функции h(t)
имеют вид
и при достаточно большом N
(27)
Положим
,
(28)
Так
как h(t) -
действительная функция, то
, n=.
Поэтому
и
.
(29)
Определим искомую функцию g(t) :
Ясно,
что
,
а из (24) и (28) следует, что
при n<0,
т.е.
(30)
В
силу соотношений (25), (27) и (29) для
,
а
для
.
Наконец,
для любого
.
Таким образом, функция g(t) обладает всеми нужными свойствами (22). Лемма1 , а вместе с ней и теорема 3 доказаны.
Теорема 4.
Пусть
функция
.
Тогда для п.в.
существует предел
(31)
При этом
1)
,
,
;
2)
;
3)
.
Доказательство:
Нам
достаточно доказать, что для каждой
функции
найдется функция
такая, что имеет место 1). Действительно,
если
,
то тем более
и из 1) и теоремы 2 вытекает справедливость
равенства (31) для п.в.
.
При этом
и по теореме 1
.
Наконец, из 1) следует, что
а тогда
.
Пусть
.
Для построения искомой функции
положим
,
,
.
Функции
,
,
имеют равномерно ограниченную по r
вариацию на
:
.
Следовательно,
по теореме Хелли [2]
найдутся функция
ограниченной вариации
и последовательность
, такие, что
в каждой точке
и
(32)
для
любой функции
.
При этом для n=1,2,...
(мы
учли аналитичность функции F(z)
в единичном круге) и , следовательно, по
теореме 3
абсолютно непрерывна : существует
функция
,
для которой
,
Тогда
,
(33)
Зафиксируем
число
. Функция
,
аналитична в круге
,
поэтому согласно утверждению 1
,
.
В
пределе при
из последнего равенства вытекает, что
,
,
.
Равенство 1) , а вместе с ним и теорема 4 доказаны.
§I.3.Пространства
и
.
Обозначим
через
класс тех
функций
,
,
которые являются граничными значениями
функций из
,
т.е. представимы в виде
для п.в.
,
.
В
силу пунктов 3)
и 2) теоремы 4
и каждая
функция
удовлетворяет условию (16). С другой
стороны, выше мы доказали, что для
произвольной
с условием (16) интеграл Пуассона (17)
определяет функцию из
.
Следовательно,
.
(34)
Из
(34) вытекает, что
(замкнутое)
-
подпространство
пространства
,
а
- банахово пространство с нормой (15).
Пусть
.
Положим
,
,
(35)
ОпределениеI.5.
Если
функция
,
то сопряженной к ней функцией называется
функция
,
,
где
интеграл понимается в смысле главного
значения, т.е. как предел при
интегралов
.
В дальнейшем нам понадобится
Утверждение2.
Для
любой функции
сопряженная функция
существует и конечна п.в. на
;
при этом
а)
, y>0;
б)
если
,
,
то
и
.
Теорема 5.
Следующие
условия эквивалентны
:
а)
;
б)
,
,
,
;
в)
;
г)
, где
-
такая действительная функция, что ее
сопряженная
также принадлежит пространству
:
.
(36)
Доказательство:
Эквивалентность условий а) и б) непосредственно вытекает из (34), а эквивалентность условий а) и в) - из теорем 4 и 2.
Докажем,
что из г) следует б). Для этого достаточно
проверить, что в случае, когда функция
и ее сопряженная суммируемы :
,
имеют место равенства
,
(37)
Непосредственный подсчет по формуле (36) показывает, что
,
,
,
.
Следовательно, равенства (37) выполняются,
если
-
произвольный тригонометрический
полином.
Пусть
фиксировано. Для произвольной функции
и
положим
,
,
где
,
,
.
Покажем,
что равенство (37) для фиксированного
нами номера n
вытекает из следующих свойств функций
(наличие этих свойств мы установим
ниже):
1)
,
,
;
2) при
функции
,
,
сходятся по мере к
;
3)
,
,
,
где С - абсолютная константа.
Итак, предположим, что имеют место соотношения 1) - 3).
Легко
видеть, что
,
где
,
поэтому из 2) вытекает сходимость по
мере последовательности функций
,:
по мере
.
(38)
Для
произвольного
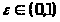найдем тригонометрический полином
такой, что
,
. (39)
Тогда согласно 3)
(40)
и
при
.
(41)
Так
как
- полином, то
и
. (42)
Учитывая,
что
,
и пользуясь оценками (40)-(42), мы находим
,
,
что вместе с (38) доказывает равенство (37).
Докажем
теперь, что для произвольной функции
справедливы соотношения 1)-3). Оценка 1)
сразу следует из неравенства Чебышева,
так как
.
Чтобы
доказать 2), фиксируем произвольное
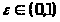и представим функцию
в
виде
,
,
. (43)
Из
непрерывности функции
легко следует, что
равномерно по
.
Поэтому при достаточно больших
с учетом (43) мы будем иметь
,
(44)
Кроме того, в силу 1) и (43)
;
из
этого неравенства и (44) вытекает, что
при
.
Для доказательства оценки 3) заметим, что
,
где
.
Применяя неравенство а) утверждения 2
для функции
и
учитывая, что
,
получим 3).
Свойства 1)-3) доказаны. Тем самым установлено, что из условия г) в теореме 5 следует б). Для завершения доказательства теоремы 5 достаточно показать, что из в) вытекает г).
Пусть
(
,
,
)
и
.
Тогда по теореме 4
,
и надо доказать только, что
для п.в.
.
Так как
ядро Пуассона - действительная функция,
мы можем утверждать, что при
и
,
.
С другой
стороны, из 2), 8) и (37) вытекает, что для
любого
,
,
.
(45)
Согласно теореме 1
.
(46)
Кроме
того, в силу утверждения 2, из сходимости
()
следует сходимость по мере функций
к
.
Таким образом,
по мере (),
а
потому , учитывая (46),
для п.в.
.
Теорема 5 доказана.
Следствие 1.
а) Если
,
то
;
б) если
и
,
то
;
в) если
,
,
,
,
то
.
(47)
Доказательство.
Соотношения а) и б) сразу следуют из эквивалентности условий а) и г) в теореме 5.
Чтобы получить в), положим
,
.
Согласно
теореме 5
,
,
а следовательно,
.
Но тогда (для п.в.
)
,
и из определения класса
мы получим, что
.
(48)
Из (48) непосредственно вытекает равенство (47).
Замечание 3.
Если
,
то в силу п. г) теоремы 5 и утверждения 2
пространство
совпадает с
.
Для р=1 это не так. Пространство
уже, чем
,
и состоит согласно п. г) теоремы 5 из
функций
,
для которых и
.
- банахово пространство с нормой
.
(49)
Полнота
с нормой (49) следует из утверждения 2 и
полноты пространства
:
если
при
,
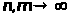то
,
,
,
и так как
по
мере при
,
то
и
при
.
Замечание 4.
Согласно
замечанию 3 равенство (47) выполняется,
в частности, в случае, когда
,
,
,
.
Отметим
также, что, взяв в (47) вместо
функцию
и учитывая б), мы получим
,
если
.
(50)
§I.4.Произведение Бляшке,
нетангенциальная максимальная функция.
Пусть
последовательность ненулевых комплексных
чисел (не обязательно различных) -
удовлетворяет условию
,
,
.
(51)
Рассмотрим произведение(произведение Бляшке)
.
(52)
Для
фиксированного
,
,
при
имеет место оценка
.
(53)
Так
как ряд (51) сходится, то из (53) легко
вывести, что произведение (52) сходится
абсолютно и равномерно в круге
,
т.е. функция
аналитична в единичном круге и имеет
нули в точках
,
,
и только в этих точках. При этом, пользуясь
неравенством
(
,
),
мы находим
,
.
(54)
Допустим
теперь, что
()
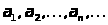- нули некоторой функции
с
,
причем каждый из них повторяется со
своей кратностью. Докажем, что ряд (51)
сходится. Положим
,
Функция
()
аналитична в круге радиуса больше
единицы, и
,
если
. Следовательно,
и согласно п.3 теоремы 4
.
Но тогда
и
,
(55)
Так
как
,
,
то из (55) вытекает сходимость произведения
,
а значит, и сходимость ряда (51).
ОпределениеI.6.
Пусть
- аналитическая в круге
функция и
,
()
- ее нули, повторяющиеся со своей
кратностью. Пусть также
- кратность нуля функции
при
.
Произведение
(56)
называется
произведением Бляшке функции
.
Справедлива
Теорема 6.
Каждая
функция
представима в виде
,
где
не имеет нулей в круге
и
,
,
а
- произведение Бляшке функции
.
Доказательство.
Пусть
,
()
- нули функции
( или, что то же самое, нули функции
)
Тогда, как отмечалось выше,
- аналитическая в круге
функция и
,
.
(57)
При
этом функция
также аналитична в единичном круге, не
имеет в нем нулей и
.
Для доказательства обратного неравенства рассмотрим частные произведения (56):
,
,
.
Так
как
для любого
,
то по теореме 4
и
, если
.
Устремив
в последнем неравенстве число
m к бесконечности и
учитывая, что
(
)
равномерно по
,
мы получим
,
,
т.е.
,
.
Теорема 6 доказана.
ОпределениеI.7.
Пусть
,
,
- произвольное число. Обозначим через
,
,
область, ограниченную двумя касательными,
проведенными из точки
к окружности
,
и наибольшей из дуг окружности, заключенных
между точками касания ( при
вырождается в радиус единичного круга).
Для
положим
,
,
где
- интеграл Пуассона функции
.
Функция
называется нетангенциальной максимальной
функцией для
.
В силу теоремы 2
для п.в.
.
(58)
Установим,
что для произвольной функции
величина
не превосходит (по порядку) значения
максимальной функции
*)
в точке х, т.е.
,
.
(59)
Нам понадобится
утверждение 3.
а)
если функция
,
то для любого
;
б)
если функция
,
то
,
где
- постоянная, зависящая только от числа
р.
Пусть
и
.
По определению интеграла Пуассона
Положим
.
Тогда будем иметь
и,
в силу неравенства
,
,
и периодичности
,
.
(60)
Так
как обе функции
и
положительны при
и отрицательны при
( из (5)), то, предполагая без ограничения
общности, что
,
мы получим
.
(61)
Для
имеют место оценки
,
.
Следовательно, для доказательства неравенства (59) достаточно проверить, что
при
,
(62)
если
.
Пусть
,
тогда
.
В
остальных случаях неравенство (62)
очевидно. Из (58), (59) и утверждения 3
вытекает, что для любой функции
,
,
,
(63)
где
- постоянная, зависящая только от
.
Теорема 7.
Пусть
(),
и
,
.
Тогда
и
.
(64)
Доказательство.
Утверждение
теоремы 7 в случае, когда
,
есть прямое следствие оценки (63) и теоремы
4. Пусть теперь
.
По теореме 6
,
где
,
,
если
и
.
Из функции
можно извлечь корень: существует функция
такая, что
,
и, следовательно из (64) при р=2, получим
.
Оценка
снизу для
вытекает из (58).
Теорема 7 доказана.
Глава II. Атомические разложения функции
в
пространстве
,
пространство ВМО.
§II.1.Пространство
,
критерий принадлежности функции из
пространству
.
Рассмотрим
()
- пространство функций
,
являющихся граничными значениями
действительных частей функций из
пространства
:
для п.в.
,
.
(65)
Ранее мы доказали, что
,
,
(66)
и что
-
банахово пространство с нормой
;
(67)
при этом, если в (65)
,
то
()
. (68)
В
замечании 3 уже говорилось о том, что
при
пространство
совпадает с пространством
и из утверждения 2 следует, что
().
Последнее
соотношение теряет силу при
- нетрудно проверить, что при
,
где
и,
следовательно, существует функция
,
для которой
.
Таким образом,
- собственное подпространство в
.
Ниже мы дадим критерий принадлежности
функций к пространству
.
ОпределениеII. 8.
Множество
мы будем называть обобщенным интервалом,
если
- дуга на единичной окружности, т.е.
- либо интервал из
,
либо множество вида
().
(69)
Точку
назовем центром обобщенного интервала
,
если
- центр дуги
.
Длиной обобщенного интервала
естественно назвать величину
Определение II.9.
Действительную
функцию
назовем атомом, если существует обобщенный
интервал
такой, что
а)
;
б)
;
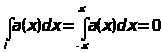в)
.
Атомом
назовем также функцию
,
.
Теорема 8.
Для
того, чтобы выполнялось включение:
,
необходимо и достаточно, чтобы функция
допускала представление в виде*)
,
,
(70)
где
,
,
- атомы. При этом
,
(71)
где
inf
берется по всем разложениям вида (70)
функции
,
а с и С
- абсолютные константы.
Доказательство.
Достаточность.
Пусть
для функции
нашлось разложение вида (70). Покажем,
что
и
. Для этого достаточно проверить, что
для любого атома
имеет место неравенство
.
(72)
Пусть
-
такой обобщенный интервал, что
,
,
(73)
(случай
тривиален). Так как
, то нам остается доказать, что
.
(74)
Для
любого измеримого множества
,
применяя неравенство Коши и пользуясь
утверждением 2 и соотношениями (73), мы
находим
,
(75)
откуда
сразу вытекает (74), в случае, когда
.
Допустим
теперь, что
,
и обозначим через
обобщенный интервал длины
с тем же центром, что и
.
Из (75) следует, что
.
Нам
остается оценить интеграл
.
Мы воспользуемся очевидным неравенством
,
,
где
-
длина наименьшей из двух дуг единичной
окружности, соединяющих точки
и
,
а
- абсолютная постоянная. В силу (73) при
мы имеем
где
-
центр обобщенного интервала
.
Из последнего соотношения, учитывая,
что
и
,
мы находим
,
,
где
.
Следовательно,
.
Оценка (74), а потому и оценка (72) доказаны.
Необходимость.
Построим
для данной функции
разложение (70), для которого
.
Пусть
функция
с
такова, что выполнено соотношение (65),
и пусть
(
)
- нетангенциальная максимальная функция
для
,
т.е.
,
,
(75')
где
-
область, ограниченная двумя касательными,
проведенными из точки
к окружности
,
и наибольшей дугой окружности
,
заключенной между точками касания.
Теорема
7 утверждает, что
,
поэтому нам достаточно найти такое
разложение функции
на атомы (70), что
,
(76)
где
постоянные С и
()
не зависят от
.
Для построения разложения (70) с условием
(76) фиксируем число
:
пусть, например,
.
Не ограничивая общности, мы можем
считать, что
.
(77)
Рассмотрим
на отрезке
множества
,
,
(78)
Так
как при любом
множество точек единичной окружности
открыто, то ясно, что при
множество
(если оно непустое) представимо
(единственным образом) в виде суммы
непересекающихся обобщенных интервалов:
,
при
,
,
.
(79)
Положим
и при
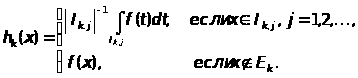(80)
Так
как
конечна для п.в.
,
то из определения функций
,
,
следует, что для п.в.
при
,
а значит, для п.в.
.
Отсюда,
учитывая, что
,
а следовательно из (80),
при
,
мы находим, что
,
(81)
где
-
характеристическая функция множества
.
Из (81), учитывая, что
,
мы для функции
получаем следующее разложение:
для п.в.
,
(82)
где
,
,
(83)
С
помощью функций
мы и построим нужное нам разложение
вида (70). Прежде всего отметим, что при
,
,
. (84)
Докажем
теперь, что для п.в.
,
, (85)
где
постоянная
зависит только от числа
,
зафиксированного нами ранее.
Так
как из (65) и (75')
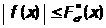для п.в.
, то из (77) следует, что
.
Пусть
теперь
,
- один из обобщенных интервалов в
представлении (79), тогда из (77) и (78)
, и если
,
- концевые точки дуги
(
)
, то
,
а значит,
,
.
(86)
Из неравенств (86) согласно (75') следует, что
при
.
(87)
Легко
видеть (учитывая, что
и
)
, что множества
и
пересекаются в одной точке:
с
,
.
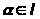(88)
Пусть
,
,
- отрезок, соединяющий точки
и
.
Так как
,
,
то из непрерывности функции
при
и
неравенства (87) вытекает, что
,
если
,
,
и
.
Поэтому , учитывая (88)
,
,,
.
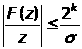(89)
|
Рассмотрим
область
отрезками
пусть,
далее, для
|
|
,
ограниченную
и
и дугой
,
,
По
теореме Коши [5]
.
Отсюда
и из (89), учитывая, что для любой дуги
справедливо равенство
,
мы получим
.
Но в силу теорем 4 и 5
,
,
и
так как
,
,
то мы находим, что
. (89')
Легко
видеть, что отношение
ограничено сверху числом, зависящим
только от ,
поэтому
,
.
(90)
Так
как
,
то из соотношений (90) и (80) вытекает, что
для
,
,
справедливо неравенство (85). Для п.в.
неравенство (85) сразу следует из
определения функций
и множеств
.
Пользуясь
оценкой (85) , из (83) мы получаем, что
,
а это значит, что функции
,
,
,
являются
атомами. Тогда, преобразуя неравенство
(82), мы получаем разложение функции
на атомы:
для п.в.
,
где
,
.
Оценим сумму модулей коэффициентов указанного разложения. Учитывая равенство (77), имеем
.
Неравенство (76), а потому и теорема 8 доказаны.
§II.2.
Линейные ограниченные функционалы на
,
двойственность
и ВМО.
Дадим
описание пространства
,
сопряженного к банахову пространству
.
Нам потребуется
Определение II.10.
Пространство
ВМО есть совокупность всех функций
,
удовлетворяющих условию
, (91)
где
, а sup берется по
всем обобщенным интервалам
.
Нетрудно убедится, что ВМО является банаховым пространством с нормой
. (92)
Ясно,
что
. В то же время ВМО содержит и неограниченные
функции. Нетрудно проверить, например,
что функция
.
Теорема 9.
,
т.е.
а)
если
,
и для произвольной функции
рассмотреть ее разложение на атомы (по
теореме 8):
,
,
,
- атомы*)
(93)
и положить
, (94)
то
сумма
ряда (94) конечна, не зависит от выбора
разложения (93) и задает ограниченный
линейный функционал на
;
б)
произвольный ограниченный линейный
функционал
на
представим в виде (94), где
.
При этом
(С, С>1> - абсолютные постоянные).
Лемма 2.
Пусть
функция
такова, что для любого обобщенного
интервала
найдется постоянная
,
для которой
,
где
М не зависит от
.
Тогда
и
.
Доказательство.
Для
любого обобщенного интервала
мы имеем
,
откуда согласно (91) получаем утверждение Леммы 2.
Следствие 2.
Если
,
то
и
.
(95)
Следствие 2 непосредственно вытекает из леммы 2, если учесть, что
для
произвольного обобщенного интервала
.
Доказательство теоремы 9.
а)
Пусть
.
Положим
Так
как всегда
, то, учитывая равенства
,
,
,
мы с помощью следствия 2 находим
,
(96)
Допустим,
что
( по утверждению 2 и (66)). По теореме 8
существует разложение
,
, (97)
где
функции
являются атомами и
,
и при
,
,
.
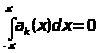(98)
Из
соотношений (96), (97) и (98) вытекает, что
при
.
Отсюда,
учитывая, что функции
,
,
по модулю не превосходят суммируемой
функции
и для п.в.
,
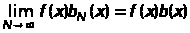мы получим, что
.
Таким образом, равенством
,
,
(99)
определяется
ограниченный линейный функционал на
всюду плотном в
линейном многообразии (плотность функций
из
в
вытекает из теоремы 8, так как для всякой
функции
частные суммы разложения (70) сходятся
к
по норме
,
и, очевидно, принадлежат пространству
).
Поэтому функционал
можно единственным образом продолжить
на все пространство
:
,
.
(100)
Остается
доказать, что для любого разложения
вида (93) функции
ряд (94) сходится и его сумма равна
.
Последнее сразу следует из (99) и сходимости
ряда (93), по норме
к
:
.
б)
Пусть L
- произвольный ограниченный линейный
функционал на
.
Тогда из теоремы 4.1 и (67) для любой функции
(С
- абсолютная постоянная). Это значит,
что L
- ограниченный линейный функционал на
,
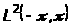а следовательно, найдется функция
с
, (101)
для которой
,
.
(102)
В
частности, равенство (102) выполняется,
если
-
произвольный атом. Докажем, что
.
(103)
Пусть
I -
произвольный обобщенный интервал,
- произвольная функция с
.
Тогда функция
,
,
является
атомом и в силу теоремы 8
.
Поэтому
.
Подбирая
в последнем неравенстве функцию
оптимальным образом, мы получим, что
для любого обобщенного интервала
I
,
что
с учетом соотношения
доказывает оценку (103).
Таким
образом, для
значение функционала
совпадает со значением ограниченного
линейного функционала
на элементе
(см. (99) и уже доказанное утверждение а)
теоремы 9). Так как пространство
плотно в
,
то, следовательно,
для любой функции
.
Полученное равенство завершает доказательство теоремы 9.
Литература
Кашин Б.С., Саакян А.А. Ортогональные ряды — М.: Наука, 1984.—495с.
Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа — М.: Наука, 1989. — 623с.
Тер-Крикоров А.М., Шабунин М.И. Курс математического анализа — М.: Наука, 1988. —815с.
Бари Н.К. Тригонометрические ряды —М.: Гос. издательство физико-математической литературы, 1961. —936с.
Маркушевич А.И. Краткий курс теории аналитических функций - М.: Наука, 1978. — 415с.
Дж.Гарнетт Ограниченные аналитические функции — М.: Мир, 1984. - 469с.
Фихтенгольц Г.М. Основы математического анализа — М.: Наука, 1964.—т.2,—463с.
Вартанян Г.М. Аппроксимативные свойства и двойственность некоторых функциональных пространств — Одесса, 1990 —111с.
*) Мы считаем , что f (x) = 0 , если x .
*)
Так как функция
определялась для функций
,
заданных на
,
то мы дополнительно полагаем
,
если
;
при
и
при
.
*)
В силу условий а) и в) в определении 9
,
,
поэтому ряд (70) сходится по норме
пространства
и п.в.
*)
Возможен случай, когда
при
.