Аксиоматика векторного пространства (работа 1)

Глава 2

1. Некоторые векторные равенства

Среди векторных соотношений можно выделить несколько важных соотношений, называемых здесь основными. Эти основные соотношения являются, образно выражаясь, ключами к решению широкого класса задач.

I Основное соотношение. Во всяком треугольнике ЛВС выполняется равенство

(I)

Где М – центроид (точка пересечения медиан) треугольника АВС.

Докажем соотношение (I).

Пусть М – центроид треугольника АВС. Соединим точку М со всеми вершинами треугольника. Прямая МВ пересекает сторону АС треугольника АВС в точке О, являющейся серединой стороны АС. На прямой ВМ откладываем МЕ = ВМ и соединяем точку Е с вершинами А и С. очевидно, что АМСЕ –параллелограмм. Поэтому . Откуда . Так как , то . Ч.т.д.

Задача. Доказать, что если М – центроид треугольника АВС и О -произвольная точка пространства, то выполняется равенство

(1)

Доказательство:

Запишем следующие векторные равенства:

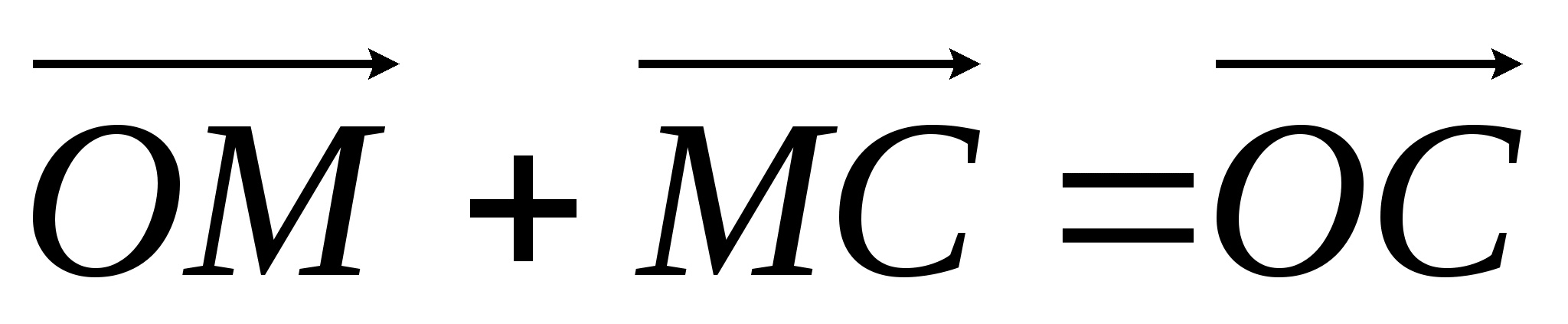
Сложив эти равенства по частям, получаем:

откуда

Доказанное равенство также следует отнести к основным векторным соотношениям, так как оно часто используется в решении многих задач.

II Основное соотношения. В треугольнике АВС на стороне АС взята точка D так, что АD : DС = m : n.

Тогда имеет месть следующее соотношение:

(II)

Доказательство:

Из треугольника АВС имеем:

Ч.т.д.

Задача. Через середину Е медианы СС_>1> треугольника АВС проведена прямая АЕ, пересекающая сторону ВС в точке F. Вычислить АЕ : ЕF и СF : FВ.

Решение.

Введем векторы и . Пусть СF : FВ = m : n. Тогда по формуле (II) имеем:

и (1)

где 0 < х < 1.

С другой стороны, учитывая, что Е – середина медианы СС_>1> получаем для АЕ следующее выражение:

(2)

В силу единственности разложения вектора по двум векторам из (1) и (2) получаем систему:

(3)

Разделив по частям первое уравнение системы (3) на второе, получаем, что m : n = 1 : 2, т.е. СF : FВ = 1 : 2.

Сложив по частям уравнение системы (3), находим, что , т.е. AE : EF = 3 : 4

III Основное соотношение. Если точки М и N делят отрезки АВ и CD соответственно в равных отношениях так, что AM : MB = CN : ND = m : n, то выполняется равенство.

(III)

Доказательство:

Для доказательства равенства (III)
мы воспользуемся формулой (II). Запишем, что отрезки АВ и CD могут произвольно располагаться относительно друг друга (например, они могут лежать на скрещивающихся прямых и на прямых, принадлежащих одной плоскости).

Пусть О - произвольная точка, не принадлежащая ни отрезку АВ, ни отрезку CD. Соединим точку О с точками А, М, В, С, N и D и раcсмотрим векторы и .

Имеем:

Ч. т. д.

Задача. На прямой m даны три точки Р, Q, R, а на прямой m_>1> -три точки P_>1>, Q_>1>, R_>1> причем , . Доказать, что середины отрезков PP_>1>, QQ_>1> и RR_>1> принадлежат одной прямой.

Решение.

Пусть М, N и К - середины отрезков РР_>1> QQ_>1> и RR_>1> соответственно.

На основании (III) запишем следующие векторные равенства:

(1)

(2)

Из (1) и (2) следует, что векторы и коллинеарные. А так как начало одного из них является концом другого, то точки М, N и К принадлежат одной прямой.

IV Основное соотношение. Дан тетраэдр ABCD и в плоскости его грани ABC точка М. Доказать, что для разложения

Выполняется равенство

Доказательство:

Допустим, что точка М лежит внутри треугольника ABC. Проведем через точки А и М прямую, которая пересекает сторону ВС в точке Е. Пусть Е делит сторону ВС в отношении m : n, т.е.

BE : EC = m : n.

Тогда по формуле (II)

Пусть далее точка М делит отрезок АЕ в отношении p : q, т.е. AM : ME = p:q. Тогда

Откуда

Ч. т. д.

2. Применение векторов к решению геометрических задач

В ряде случаев при решении задач на вычисление применение векторов предпочтительнее конструктивных подходов, связанных с использованием дополнительных построений, применения элементарной алгебры и тригонометрии.

Чтобы успешно решать геометрические задачи посредством векторов, требуется не только знание законов векторной алгебры, знакомство с понятием разложения вектора в базисе , умение переводить геометрический факт на язык векторов, но и определенная методика при составлении плана решения. Отметим несколько важных положений.

1. Если требуется вычислить расстояние или угол, то надо применять скалярное умножение векторов.

2. При введение векторов можно идти двумя путями:

а) выбрать точку от которой откладывается известные векторы;

б) векторы изображать направленными отрезками, связанными с рассматриваемыми в задаче фигурами, не откладывая их от одной точки.

3. Если задача планиметрическая, то целесообразно выделить два неколлинеарных вектора в качестве базисных и остальные векторы выразить через них; если же задача стереометрическая, то в качестве базиса следует выбрать три некомпланарных вектора. При этом введение начальной точки необязательно.

4. В ряде случаев, например при решении задач на многогранные углы,

вычисления упрощаются, если ввести единичные векторы, отложенные от вершины многогранного угла.

Примеры задач, решаемых векторным методом.

Задача. Вычислить тупой угол, образованный медианами, проведенными из вершин острых углов равнобедренного прямоугольного треугольника.

Решение.

Пусть и ;

Согласно условию .

Вектор 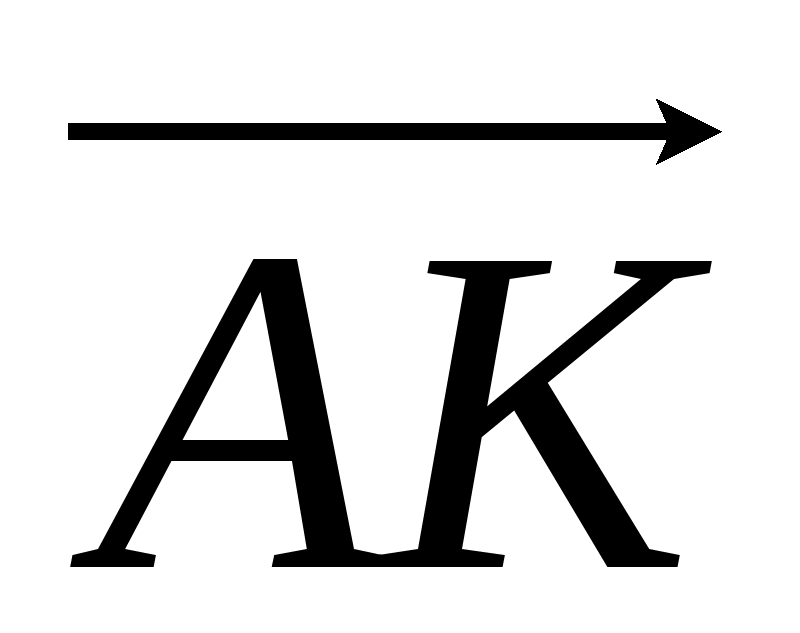есть разность векторов и , т.е. _>> (т.к. _>>).

Аналогично _>>.

Угол между векторами находится по формуле:

_>>

_>>,

но, _>>, т.к. _>>. Следовательно

_>>_>>.

длины векторов _>>и _>> найдем по теореме Пифагора.

_>>

Таким образом _>>

Тогда _>>

Ответ: _>>

Задача. На ребрах прямоугольного трехгранного угла с вершиной О отложены равные отрезки ОА, ОВ, ОС. Из точки О на плоскости ABC опущен перпендикуляр ОН. Доказать, что если точка Н_>1> симметрична точке Н относительно вершины О, то тетраэдр Н_>1> ABC правильный.

Решение:

Примем вершину О трехгранного угла за начало векторов. Тогда

и .

Следовательно,

Найдем

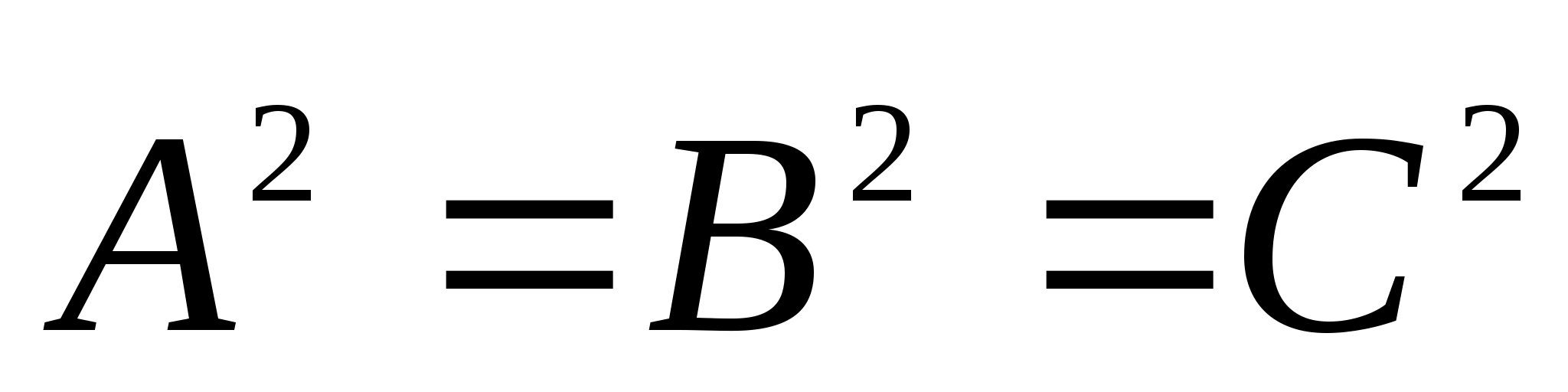Учитывая, что и , имеем: .

Далее находим:

Это значит , что отрезки H_>1>A и H_>1>B равны и образуют угол 60°, т.е. треугольник H_>1>AB правильный.

Аналогично устанавливается, что две другие грани H_>1>BC и H_>1>CA являются равносторонними треугольниками и вследствие этого тетраэдр правильный.

Задача. Доказать, что можно построить треугольник, стороны которого равны и параллельна медианам данного треугольника ABC.

Решение.

Обозначим середины сторон ВС, СА и АВ соответственно А’, B’, C’. Выразим векторы, представляющие медианы треугольника ABC, через , , (через стороны данного треугольника):

Составим сумму сторон треугольника ABC

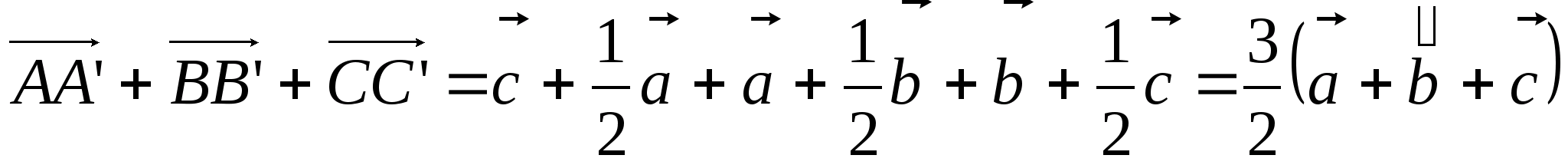Но так как векторы и образуют данный треугольник ABC, то их сумма равна нулю, следовательно, и . А это значит, что из векторов можно построить треугольник.

Задача. В треугольнике ABCD точка Е и F – середина рёбер АВ и CD соответственно. Доказать, что середины отрезков СЕ, DE, AF и BF являются вершинами параллелограмма.

Решение. Пусть К, L, М, N - середины отрезков СЕ, DE, AF и BF, соответственно. Доказать, что середины отрезков СЕ, DE, AF и BF являются вершинами параллелограмма.

Докажем равенство векторов и , выразив их через векторы , , , , где О – произвольная точка.

(1)

. (2)

Ч. Т. Д.

Задача. Точки К, L, M на сторонах АС, ВС, АВ треугольника ABC таковы, что , N – середина сторона АС. Найти отношение в котором точка пересечения отрезков KL и MN делит отрезок KL.

Решение.

Обозначим через О точку пересечения отрезков MN и KL и через х отношение KO : KL. Тогда . Учитывая, что L – середина МС и , получаем

Так как точка О лежит на прямой MN, то . Откуда . Значит, .

Ответ: KO : OL = 2:3

Задача. Отрезки DA_>1>, DB_>1>, DC_>1> – медианы граней BCD, ACD и ABD тетраэдра ABCD соответственно. Точки К, М, N делят отрезки DA_>1>, DB_>1>, DC_>1>в отношении , . В каком отношении плоскость KMN делит ребра DA и DB ?

Решение.

Пусть плоскость KMN пересекает ребра DA, DB и DC тетраэдра ABCD в точках Р, Q, R соответственно.

Точки А_>1>, В_>1>, С_>1> – середины отрезков ВС, АС, АВ соответственно. Следовательно,

Решив эту систему, (например, сложив (1) и (2), и вычтя (3) получим

Пусть . Тогда, учитывая , , ,

имеем

, и, т.к. точки К, М, N, Р лежат в одной плоскости, то

Таким образом, , откуда .

Пусть теперь , тогда

, и

, откуда

Ответ: , .

Задача. Основанием пирамиды SABC является равносторонний треугольник ABC, длина стороны которого равна . Боковое ребро SC перпендикулярно плоскости оснований и имеет длину 2. Найти угол между прямыми, одна из которых проходит через точку S и середину ребра ВС, а друга проходит через точку С и середину ребра АВ.

Решение. Обозначим .

Выберем в качестве базиса векторы , и .

Тогда, из треугольника BCS: ,

а из треугольника ABC:

Ответ: .

Задача. Каждое ребро призмы ABCA_>1>B_>1>С_>1> равно 2.

Точки М и N – середины ребер АВ и A_>1>А. Найти расстояние от точки М до прямой CN, если известно, что угол A_>1>AС paвeн 60° и прямые A_>1>A и АВ перпендикулярны.

Решение.

Рассмотрим базис, состоящий из векторов , _>>, _>> и составим таблицу умножения для этих векторов.

*	а	b	с
а	4	0	2
b	0	4	2
с	2	2	4

Расстояние от точки М до прямой CN равно расстоянию от точки М до её проекции на прямую CN.

Пусть Р – проекция точки М на прямую CN.

Тогда

для некоторого числа х.

Так как _>> и _>>,

_>>

Поскольку прямые _>> и _>> перпендикулярны, то _>> т.е.

_>>.

Раскрывая скобки и пользуясь таблицей умножения для нашего базиса, получаем: _>>.

Тогда _>>.

Искомое расстояние _>> равно

_>>

Снова раскрывая скобки и пользуясь таблицей умножения, находим _>>. Таким образом, расстояние от точки М до прямой _>> равно _>>.

Ответ : расстояние равно _>>.

у ⁶

Задача. В параллелограмма ABCD точка К – середина стороны ВС, а точка М – середина стороны CD. Найдите AD, если АК = 6, АМ = 3, угол КАМ = 60°.

Решение.

В качестве базиса выберем векторы и и составим таблицу умножения для векторов этого базиса.

*	k	m
k	36	9
m	9	9

По формуле треугольника и .

Так как X – середина ВС, М – середина CD, то и , и получаем систему:

_>>, откуда

_>>

Ответ: 4.

Задача. Ребра СА, СВ, СС, треугольной призмы ABCA_>1>В_>1>С_>1> равны, соответственно 2, 3 и 4 образуют между собой углы _>>ACB = 90°, _>>ACС_>1> = 45° и _>>BCC_>1> = 60°. Найдите объём призмы.

Решение.

Пусть отрезок С_>1>О является высотой данной призмы. Тогда _>>

Для того, чтобы найти высоту С_>1>О, выберем в качестве базиса векторы

_>> и составим

таблицу умножения.

*	_>>	_>>	_>>
_>>	4	0	_>>
_>>	0	9	6
_>>	_>>	6	16

Разложим вектор C_>1>O по векторам _>>. Получим: _>>, где _>>, а _>>.

Таким образом _>>.

Коэффициенты х, у находим из условий перпендикулярности вектора C_>1>O с векторами _>>.

_>>_>>_>>_>>_>>_>>_>>.

Следовательно, _>>

Значит С_>1>О = _>>

Тогда V = 3·C_>1>O = 3·2 = 6

Ответ: 6.

С помощью векторов можно решать не только геометрические задачи, но и доказывать алгебраические неравенства.

I. Доказать неравенство _>>

Доказательство:

Рассмотрим векторы _>> и _>>.

Их скалярное произведение _>>

Так как _>>, _>>, то, учитывая неравенство _>>, получим _>>.

II. Докажем, что для любых неотрицательных чисел a, b, c справедливо неравенство:

_>>

Доказательство:

Рассмотрим векторы _>> и _>>. Их скалярное произведение: _>>, а длины _>> и _>>. Отсюда, учитывая неравенство _>>, получаем

_>>.

Глава 1

§1. Аксиоматика векторного пространства

Характеризация векторного пространства, как математической структуры осуществляются рядом аксиом.

Основные понятия теории: "вектор", "сумма двух векторов", "произведение вектора на действительное число".

Косвенным определением основных понятий теории векторного пространства являются следующие аксиомы:

I. Для любых векторов и существует единственный третий вектор , называемый их суммой

Таким образом аксиома I постулирует:

а) единственность этой суммы.

б) существование суммы двух векторов и ;

Данная аксиома вводит на множестве векторов V операцию

f_>1>: V x V  V.

которая называется сложением двух векторов.

II. Сложение векторов коммутативно, т.е.

III. Сложение векторов ассоциативно, т.е.

IV. Существует вектор такой, что для любого вектора, т.е.

Определение 1.1. Вектор , удовлетворяющий аксиоме IV, называется нулевым вектором и обозначается

V. Для каждого вектора существует такой вектор , что +=

Определение 1.2. Вектор , удовлетворяющий аксиоме V, называется противоположным вектору .

VI. Для любого вектора и действительно числа , существует единственный вектор , называемый произведением вектора на число и обозначаемый т.о.: 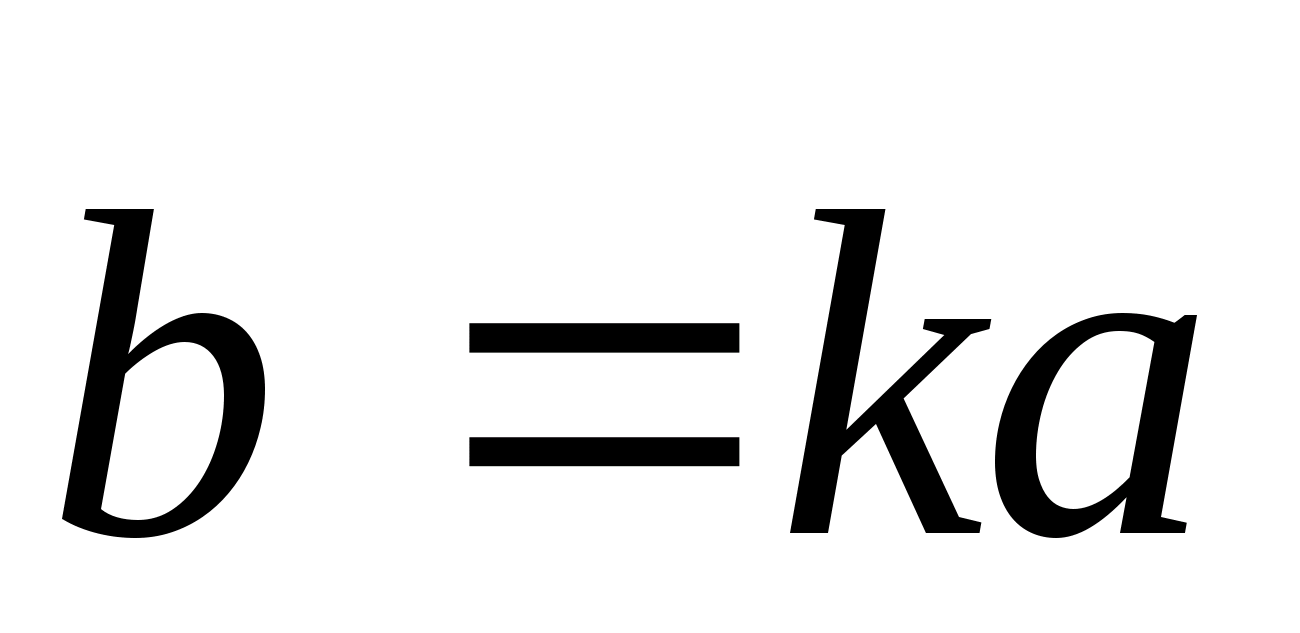, т.е.

, ,

Данная аксиома вводит операция нового типа (внешнюю операцию):

Эта операция носит название «умножение вектора на число».

VII. Для любого вектора умножение вектора на 1 не изменяет вектора , т.е.

VIII. Умножение вектора на число ассоциативно, т.е.

, ,

IX. Умножение вектора на число дистрибутивно сложения чисел, т.е.

, ,

X. Умножение вектора на число дистрибутивно относительно сложения векторов, т.е.

, ,

Этим заканчивается аксиоматика векторного пространства, которое можно теперь определить т.о.:

множество V с введенными двумя операциями

подчиняющееся аксиомам I-X, называется векторным пространством над полем действительных чисел R.

§2. Следствие из аксиом векторного пространства

Из аксиом I-X можно вывести целый ряд предложений.

Теорема 2.1. Существует единственный нулевой вектор.

Доказательство:

Предложим, что существует два различных вектора и таких, что и для любого вектора .

Положим . Тогда

и (1)

Положим теперь . Аналогично получим:

и (2)

Так как (по аксиоме II), то из (1) и (2) следует, что .

Таким образом, векторное пространство содержит единственный вектор , удовлетворяющий равенству .

Теорема 2.2. Для любого вектора существует единственный противоположный вектор .

Или:

Доказательство:

Допустим, что и и , т.е. существует , имеющий два различных противоположных вектора и .

и (1)

(2)

Тогда

и (3)

Левые части равенств (3) равны между собой. Действительно:

(4)

Из равенства (3) и (4) следует, что .

Теорема 2.3. Для любых векторов и существует единственный вектор , такой, что .

Доказательство:

I. Существование. Убедимся, что в качестве вектора можно будет выбрать вектор . В самом деле,

Таким образом, для векторов и существует вектор , удовлетворяющий равенству:

II. Единственность (от противного). Пусть

и (1)

Тогда:

Отсюда . Получим противоречие с допущением. Таким образом, единственность вектора доказана.

Определение 2.1. Вектор, удовлетворяющий равенству , называется разностью векторов и , и обозначается через - .

Таким образом

Теорема 2.3., как видно, вводит на множестве v новую операцию "–":

называемую вычитанием, которая является обратной по отношению к операции сложения.

Следствие 1.

Теорема 2.4.

Доказательство:

, т.к. 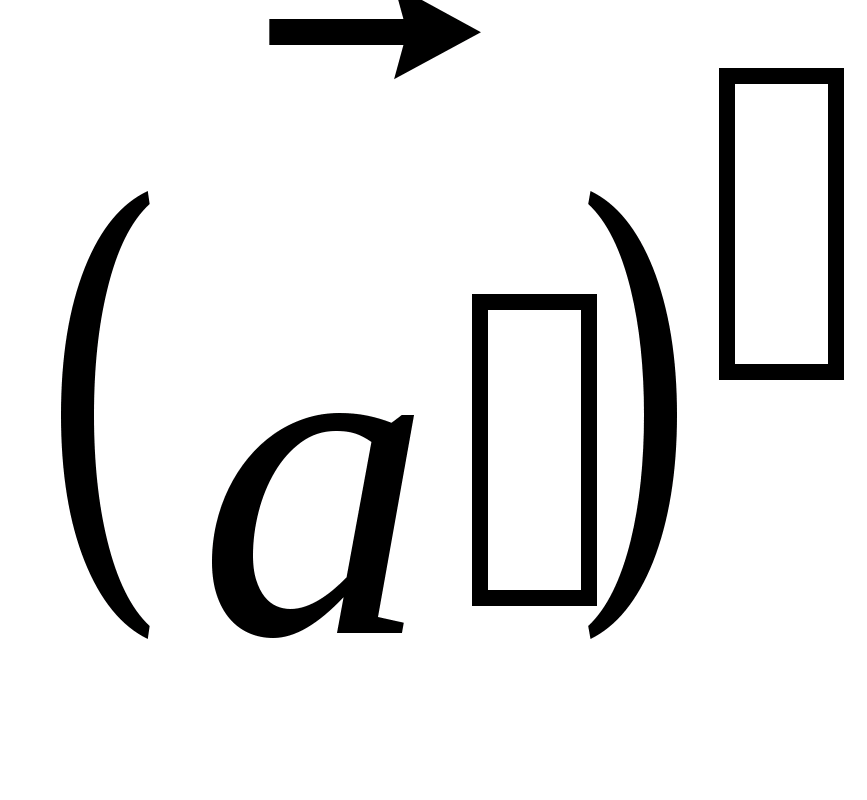- вектор, противоположный вектору . Тогда

Ч.т.д.

Теорема 2.5.

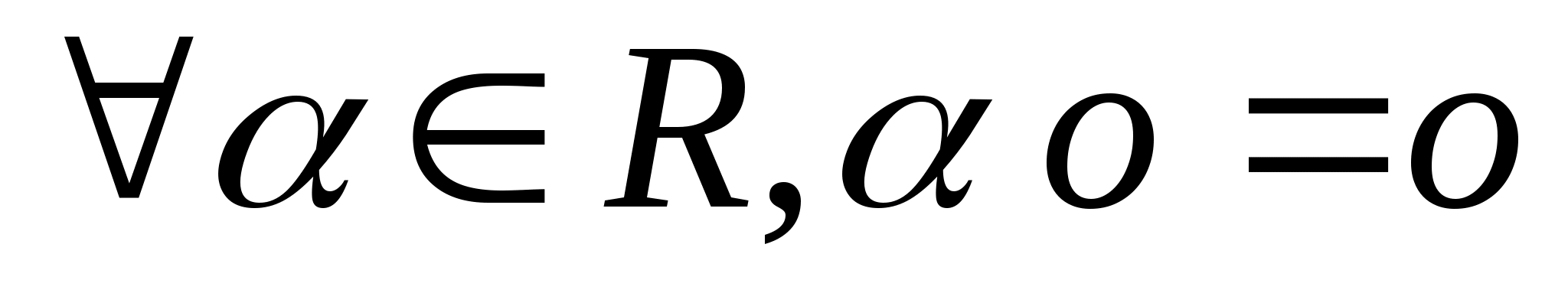
Доказательство:

Имеем:

;

Отсюда следует, что .

Ч.т.д.

Теорема 2.6. .

Доказательство:

Имеем:

Отсюда следует, что .

Теорема 2.7.

Доказательство:

Имеем:

(по Теореме 2.6.)

Отсюда следует, что .

Следствие 2. .

Теорема 2.8. или .

Доказательство:

Возможны два случая:

I. и

II. .

I. Если , то дизъюнкция или истинна и теорема доказана.

II. Пусть . Тогда существует число , отсюда имеем:

(по условию Т. 2.5.) ,

(по Т. 2.5.) .

Таким образом, в случае II имеем, что .

Итак, если , то или .

Теорема 2.9. .

Доказательство:

Для того, чтобы установить, что вектор является противоположным для вектора , необходимо и достаточно проверить, выполняется ли следующее равенство:

, или все равно, что .

Имеем:

Таким образом или . И, следовательно, .

Рассмотренные свойства операций над векторами аналогичны соответствующим свойствам арифметических операций над числом. Так, например, сумма конечного числа векторов, как и сумма в любой коммуникативной группе, не зависит ни от порядка слагаемых в этой сумме, ни от способа расстановки скобок:

и т.д.

Однако между векторной и числовой алгеброй существуют серьезные отличия. Одно из наиболее существенных отличий состоит в том, что множество векторов не является упорядоченным, т.е. для векторов нельзя ввести отношение «меньше» и «больше». Например для двух противоположных чисел и мы знаем, что и, что одно из этих двух чисел больше 0, а другое – меньше 0. Для векторов же, удовлетворяющих равенству , постановка вопроса о том, какой из векторов или больше нулевого, а какой меньше нулевого, бессмысленна.

§3. Размерность

Определение 3.1. Векторное пространство называется n-мерным, если в нем имеется n линейно независимых векторов, а всякие n+1 векторы линейно зависимы.

Иначе говоря, размерность векторного пространства – это максимальное число содержащихся в нем линейно независимых векторов.

Если максимальное число линейно независимых векторов равно 1, то векторное пространство называется одномерным, если это число равно 2,. То векторное пространство называется двумерным, и т.д.

Векторное пространство, имеющее конечную размерность, называется конечномерным. Пространство, в котором существует сколь угодно линейно независимых векторов, называется бесконечномерным.

Определение 3.2. Совокупность n линейно независимых векторов n-мерного векторного пространства называется его базой.

Теорема 3.1. Каждый вектор n-мерного векторного пространства можно представить, и притом единственным образом, в виде линейной комбинации векторов базы.

Доказательство:

Пусть – произвольная база n-мерного векторного пространства. Так как любые n+1 векторы n-мерного векторного пространства линейно зависимы, то векторы

линейно зависимы, т.е. нулевой вектор является нетривиальной линейной комбинацией векторов :

где не все равны нулю. При этом . Если бы , то тогда среди чисел хотя бы одно было отлично от нуля, а отсюда следует, что векторы линейно зависимы.

Пусть например, , тогда .

Откуда следует линейная зависимость векторов , что противоречит условию.

Итак, . Если , то

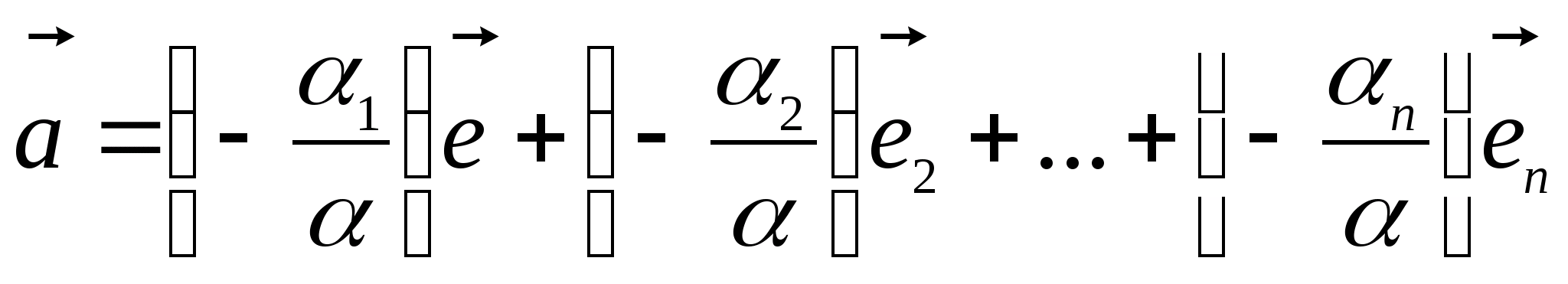
Полученное представление вектора является искомым.

Докажем, что оно единственно.

Допустим, что возможны два представления вектора в виде линейной комбинации базы:

и .

Тогда

, отсюда

Так как векторы линейно независимы, то

и, следовательно,

Ч.т.д.

Примеры.

1. Определим размерность векторного пространства геометрических векторов трехмерного пространства.

Докажем, что любые три вектора выходящие из одной точки О и не лежащие в одной плоскости, являются линейно независимыми, а всякие четыре вектора линейно зависимы.

В самом деле, векторы независимы, т.к. в противном случае один из них, например , должен был бы линейно выражаться через два других. Однако равенство : вектор является диагональю параллелограмма, построенного на векторах и . Отсюда векторы и и – компланарны, что противоречит условию их выбора.

Докажем теперь, что любые четыре вектора – линейно зависимы.

Возможны следующие случаи.

а) Векторы компланарны, тогда любая тройка векторов линейно зависима. Если система имеет подсистему линейно зависимых векторов, то эта система линейно зависима.

б) Из четырех векторов существует три компланарных, а следовательно, три линейно зависимых вектора. Как и выше, вся система векторов будет линейно зависимой.

в) Из четырех данных векторов никакие три не являются компланарными. В этом случае никакие три, а следовательно, и никакие два вектора из числа данных не являются линейно зависимыми.

Пусть .

Обозначим плоскость (OBC) через П_>1>, а плоскость (AOD) через П_>2>.

(Такие плоскости существуют, так как пара векторов и и пара векторов и - пары линейно независимых векторов). Плоскости П_>1> и П_>2> имеют общую точку О. Тогда эти плоскости имеют общую прямую m, проходящую через эту точку О.

В плоскости П_>2>построим параллелограмм OPDR с диагональю OD. Тогда , где . Вектор , лежащий в плоскости П_>1> является линейной комбинацией векторов и : . Тогда , или . Отсюда, по теореме 5.1., векторы линейно независимы.

Итак, множество геометрических векторов трехмерного евклидового пространства представляет собой трехмерное векторное пространство.

2. Пространство арифметических векторов длины n представляет собой n-мерное векторное пространство.

Докажем это.

Прежде всего, нетрудно установить существование n линейно независимых векторов. Возьмем векторы:

и докажем, что они линейно независимы. В самом деле, если допустить, что эти векторы линейно зависимы, тогда на основании теоремы 5.1. хотя бы один из них есть линейная комбинация остальных. Пусть, например, есть линейная комбинация остальных:

(1)

тогда

Отсюда

(2)

Система (2) является несовместной. Следовательно, не существует такого выбора коэффициентов , чтобы равенство (1) удовлетворялось. Таким образом, линейная независимость системы векторов доказана.

Докажем теперь, что всякие n+1 арифметические вектора линейно зависимы. Пусть имеется система из n+1 векторов:

Выясним, существуют ли числа , не все равны нулю, такие, что

(3)

Равенство (3) эквивалентно системе:

(4)

Получим систему однородных уравнений, в которых число уравнений n, а число неизвестных m=n+1. Такая система всегда имеет ненулевое решение и, следовательно, система векторов является линейно зависимой.

Контрпример. Рассмотрим совокупность всех непрерывных функций на сегменте [0; 1]. Нетрудно убедиться, что в данном случае мы имеем дело с векторным пространством над полем действительных чисел R. Пусть n – произвольное натуральное число.

Положим:

Докажем, что система векторов является линейно независимой. Запишем равенство.

Положив последовательно , , получим

Таким образом, равенство

влечет за собой равенство

Отсюда, векторы линейно независимы. Так как n – любое натуральное число, то, следовательно, векторное пространство всех непрерывных функций заданных на отрезке [0; 1] не имеет конечной системы линейно независимых векторов, для которых всякая система, содержащая на один больше векторов, была бы линейно зависима. Поэтому в этом пространстве нельзя ввести понятие конечной размерности. Такие пространства называются бесконечными.

§4. Аксиоматика Евклидово-векторного пространства

n-мерное векторное пространство называется евклидовым, если оно удовлетворяет дополнительной группе аксиом (называемыми аксиомами скалярного произведения). Эти аксиомы вводят в n-мерное векторное пространство новое понятие – понятие скалярного произведения двух векторов.

Аксиомы:

XII. Для любых двух векторов и существует единственное число , называемое их скалярным произведением.

Обозначение: - скалярное произведение векторов и .

Таким образом,

Аксиома XII утверждает по сути дела, существование отображения VxVR, ставшего в соответствие каждой паре векторов единственное число из R.

Это отображение называется скалярным умножением двух векторов.

XIII. Скалярное умножение двух векторов коммутативно:

XIV. Скалярное умножение ассоциативно относительно умножения вектора на число:

XV. Скалярное умножение диструбутивно относительно сложения векторов:

XVI. Для любого вектора и

Примеры.

1. рассмотрим трехмерное пространство геометрических векторов. Под скалярным произведением двух векторов и будем понимать число , где и длины векторов и соответственно, а  - угол между данными векторами.

Нетрудно установить, что, определив скалярное произведение таким образом, мы удовлетворим всем аксиомам скалярного произведения двух векторов. Следовательно, трехмерное пространство геометрических векторов с введенным таким образом скалярным произведением является евклидовым.

2. Рассмотрим трехмерное пространство арифметических векторов. Под скалярным произведением векторов (x_>1>;y_>1>;z_>1>) и (x_>2>;y_>2>;z_>2>) будем понимать число легко можно проверить, что аксиомы скалярного произведения двух векторов будут удовлетворены. Следовательно, трехмерное пространство арифметических векторов (с введенным таким образом скалярным произведением) является евклидовым.

3. Рассмотренный пример можно обобщить на n-мерное пространство арифметических векторов, если скалярное произведение двух векторов 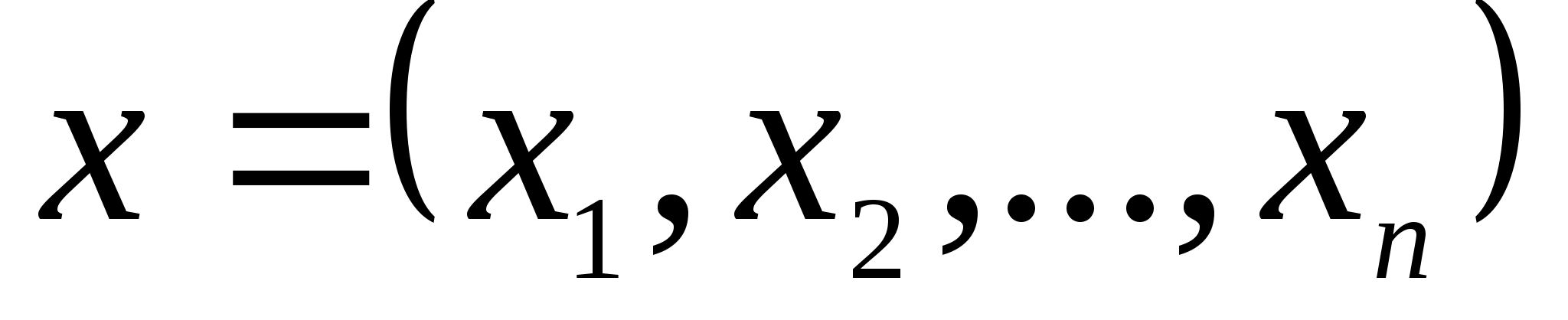и .

Определить равенством 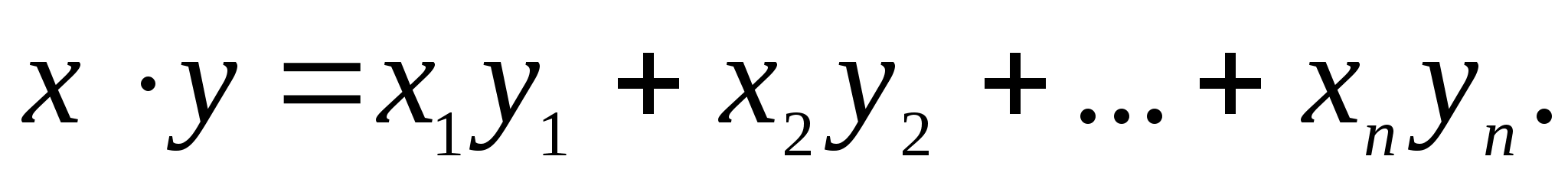(1)

Таким образом, n-мерное пространство арифметических векторов с введенным равенством (1) скалярным произведением, является евклидовым.

§5. Следствия из аксиом скалярного произведения

Доказательство:

Имеем (1). Тогда

Определение 5.1. называется длиной вектора .

Обозначение: - длина вектора .

Таким образом, .

2. . Это вытекает из принятого определения и следствия 1.

3. , где - вектор, противоположный вектору .

Доказательство:

4. Для любых и имеет место неравенство Коши-Буняковского:

Доказательство.

Рассмотрим скалярное произведение вектора на себя.

Имеем:

(XVI)

где t – любое действительное число. Отсюда на основании аксиом XIII-XV получаем:

Выражение в левой части неравенства представляет собой квадратный трехчлен относительно t. Так как этот трехчлен должен быть неотрицательным при всех значениях t, то он не может иметь двух различных корней и, поэтому, его дискриминант:

Отсюда

Определение 5.2. Число называют косинусом угла между векторами и .

Итак,

Введение такого определения оправдывается, в частности, следующими неравенствами:

Этот факт непосредственно следует из следствия 4.

5. (Неравенство треугольника)

Доказательство:

Воспользуемся неравенством Коши-Буняковского:

Откуда:

Определение 5.3. Векторы и называются ортогональными, если их скалярное произведение равно 0.

Обозначение: - и - ортогональные векторы.

Итак,

6. Существуют два ненулевых ортогональных вектора.

Доказательство:

Пусть даны два линейно независимых вектора и .

Рассмотрим два вектора: и .

Подберем l так, чтобы последнее равенство последовательно преобразуем так: =0 Þ

Таким образом, векторы и ортогональны.

В самом деле:

Кроме того, векторы f_>1> и f_>2> ненулевые.

7.(Теорема Пифагора). Если векторы и ортогональны, то

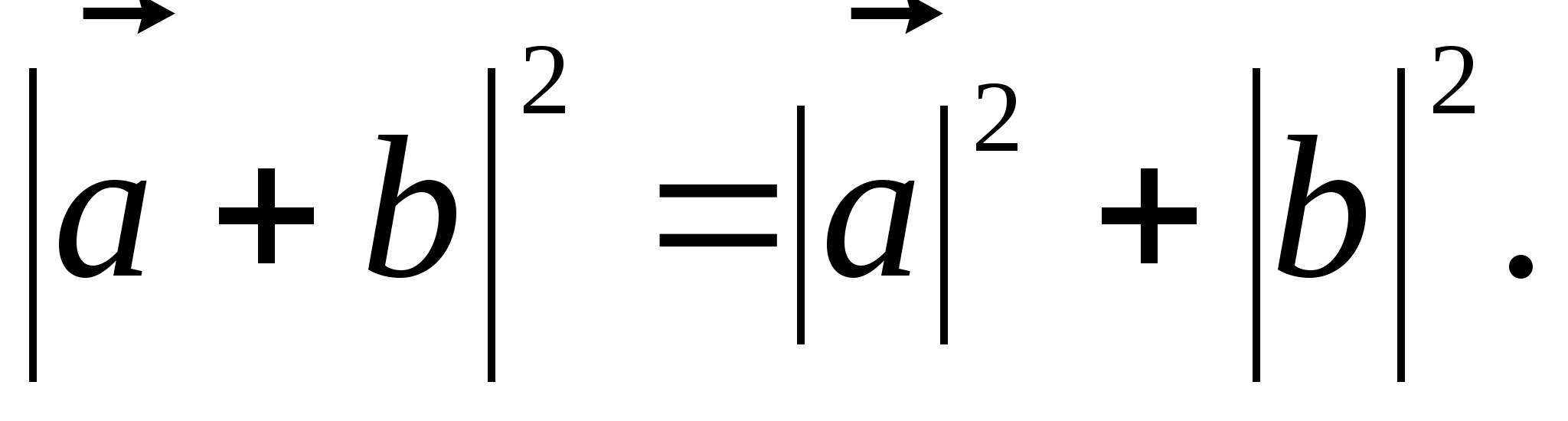
Доказательство:

Так как Тогда

Определение 5.4. База евклидова пространства называется ортогональной, если для всех

Если при этом еще при , то база называется ортонормированной.

8. Попарно ортогональные ненулевые векторы линейно независимы.

Доказательство:

Пусть векторы попарно ортогональны и все отличны от нулевого вектора. Рассмотрим равенство . Умножая обе части этого равенства последовательно на векторы , получим:

…………………………………………..

Откуда,

Так как , то из полученных равенств следует a_>1>=a_>2>=…=a_>n>=0.

Это означает, что система векторов , линейно независима.

9. Существуют три ненулевых попарно ортогональных вектора.

Доказательство:

Пусть и два ненулевых ортогональных вектора, существование которых обеспечено следствием 6. Подберем ненулевой вектор такой, что и Положим , где - вектор. Образующий с векторами и в условиях следствия 6 линейно независимую систему. Тогда

Отсюда

Имеем:

Таким образом, отправляясь от трех линейно независимых векторов и , мы построили три ненулевых вектора , которые попарно ортогональны.

Обобщение. Привлекая последовательно все базы n-мерного евклидового пространства, можно построить аналогично следующие системы ненулевых попарно ортогональных векторов:

…………..

Так как система векторов линейно независима и содержит n векторов (максимальное число линейно независимых векторов), то в результате получена в n-мерном пространстве ортогональная база .

Описанный процесс известен в математике под названием процесса ортогонализации.

Имея ортогональную базу, нетрудно получить с ее помощью ортонормированную базу. Для этого вместо каждого вектора нужно взять вектор

Убедимся, что длина этого вектора равна 1. В самом деле,

§6. Аксиоматика точечно-векторного евклидова пространства

§6.1. Метрические соотношения в треугольнике

Теорема 18.5. (теорема косинусов для треугольника).

Во всяком треугольнике

,

Доказательство:

Рассмотрим векторное равенство . Возьмем скалярный квадрат:

Пусть - единичный вектор, отложенный от точка А на луче [АВ), - единичный вектор, отложенный от точки А на луче [АС). Тогда

Отсюда

Аналогично устанавливаются остальные две формулы теоремы косинусов для треугольника.

Следствие. В треугольнике две стороны конгруэнтны тогда и только тогда, когда лежащие против них углы конгруэнтны.

Доказательство:

I. Пусть . Докажем, что .

Имеем

II. Пусть . Докажем, что . Выполним следующие преобразования

– ,

Докажем, что ; то ;

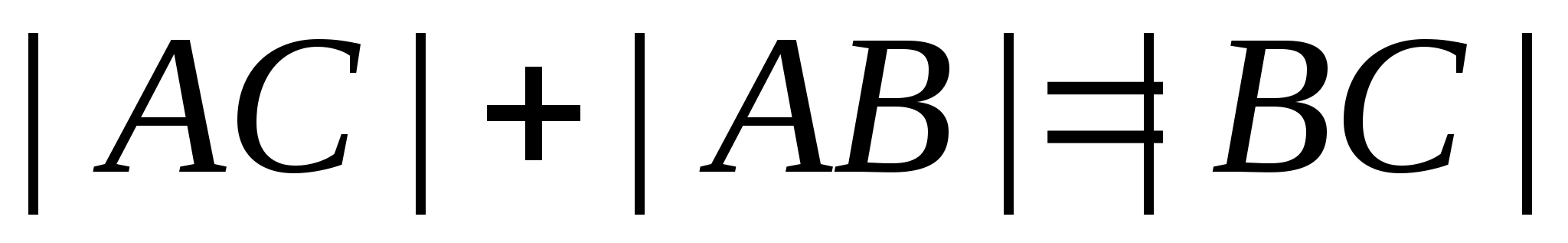, но для треугольника .

Таким образом,

Теорема 18.6.

, (1)

(2)

(3)

Доказательство:

Докажем равенство (1). Рассмотрим равенство: . Умножим его скалярно на :

, или так как , то

, или

, это и есть равенство (1).

Аналогично устанавливается остальные соотношения.

Следствие 2. Если один из углов в треугольнике тупой, то два других острые.

Доказательство:

Пусть – прямой, то есть .

Имеем:

Тогда:

– острый,

– острый.

Следствие 3. В треугольнике более одного тупого угла быть не может.

Доказательство:

Пусть – тупой угол, то есть .

Тогда – острый.

Аналогично устанавливается, что – острый.

Определение 18.6. Треугольник называется прямоугольным, если он имеет прямой угол.

Теорема 18.7. (теорема Пифагора). Если в – прямой, то .

Доказательство:

Имеем: .

Так как – прямой, то .

Тогда .

Теорема 18.8. (обратная теорема 18.7). Если в , то этот треугольник прямоугольный.

Доказательство получается в результате проведения предыдущих рассуждений в обратном порядке.

Следствие 4. В прямоугольном треугольнике каждый катет меньше гипотенузы.

Доказательство:

Пусть , тогда имеем:

Так как углы С и В острые, то и .

Отсюда и .

§6.2. Конгруэнтность треугольников

Определение 18.7. Если треугольник АВС называется конгруэнтным треугольнику А_>1>В_>1>С_>1>, если

,

Обозначение: – треугольник АВС называется конгруэнтным треугольнику А_>1>В_>1>С_>1>.

Теорема 18.9. Если , то .

Доказательство:

Имеем:

, (1)

(2)

По условию теоремы .

Отсюда и из равенств (1) и (2) следует, что , то есть

Аналогично устанавливается и соотношения , . Отсюда .

Теорема 18.10. Если и

то .

Доказательство:

На основании теоремы 18.5. имеем:

Отсюда, учитывая условия теоремы, получим , то есть .

На основании предыдущей теоремы .

Теорема 18.11. Если , и , .

Доказательство:

Если , то доказанному выше . Если , то отложим на луче [АС) от точки А отрезок [А_>1>С_>1>] (рис.):

. Тогда на основании предыдущей теоремы . Из конгруэнтности этих треугольников следует, что . Имеем: на луче [ВА) в полуплоскости, содержащей точку С, отложены два угла (различных) и , конгруэнтных одному и тому же углу . Последнее противоречит теореме 18.4., следовательно и .

§7. Элементы тригонометрии

§7.1. Билинейная кососимметричная функция

Определение 19.1. Если каждым двум векторам и ставится в соответствие каждое действительное число такое, что:

1) ;

2) ;

3) .

то функция называется билинейной кососимметрической функцией.

Теорема 19.1. Пусть и – произвольная база плоскости и – некоторое действительное число. Тогда существует одна и только одна кососимметрическая функция такая, что:

Доказательство:

Пусть в заданном базисе два произвольных вектора и имеют разложения:

Составим функцию

(1)

Нетрудно проверить, что билинейная кососимметрическая функция, причем, если , то

Доказательства единственности. (методом от противного).

Допустим, что существует билинейная кососимметрическая функция

, такая, что .

Если – билинейная функция, то

= =

= .

Учитывая, что , получим .

Аналогично . Кроме того, . Тогда

По предположению . Поэтому:

_>>(2)

Из (1) и (2) следует, что .

Примечание. Из проведенного рассуждения видно, что какое бы число мы ни взяли и какую бы мы ни взяли базу векторов и , существует единственная билинейная кососимметрическая функция такая, что .

Это обстоятельство говорит, что с помощью кососимметрической функции нельзя отличить ортонормированную базу от прочих. На этот счет требуется специальное соглашение. Договоримся, если база ортонормированная, то будем полагать .

Определение 19.2. Пусть – два произвольных единичных вектора. Значение билинейной кососимметрической функции при выбранном ортонормированном базисе , и выполнении соглашения называется синусом угла между векторами и .

Итак,

В иной форме:

Теорема 19.2. или . На основании определения 19.2. имеем:

Отсюда,. Докажем достаточность. Пусть , где .

Докажем, что .

В силу определения 19.2. имеем:

Теорема 19.3. .

Доказательство:

Пусть – единичные векторы и .

Имеем:

Тогда

§7.2. Геометрическое истолкование косинуса и синуса угла между двумя единичными векторами

В

На основании соотношения

Для произвольного треугольника имеем (рис.).

Так как , то

Наша окружность единичного радиуса ,

поэтому:

Таким образом, косинус угла между двумя единичными векторами и есть длина отрезка, который является проекцией отрезка [ОВ] на прямую (ОА), причем эта длина берется со знаком «+» если и со знаком «–» если .