Пример решения задачи по разделу «Переходные процессы»

Пример решения задачи по разделу «Переходные процессы»

Задача. Дана электрическая цепь, в которой происходит коммутация (Рис. 1). В цепи действует постоянная ЭДС Е. Требуется определить закон изменения во времени токов и напряжений после коммутации в ветвях схемы.

Задачу следует решить двумя методами: классическим и операторным. На основании полученного аналитического выражения построить график изменения искомой величины в функции времени в интервале от t = 0 до t = , где – меньший по модулю корень характеристического уравнения.

Параметры цепи: R_>1> = 15 Ом; R_>2> = 10 Ом; С = 10 мкФ; L = 10 мГ; Е = 100 В.

Решение.

Классический метод.

Решение задачи получается в виде суммы принужденного и свободного параметра:

i(t) = i_>пр>(t) + i_>св>(t); u(t) = u_>пр>(t)+ u_>св>(t), (1)

где , а .

1. Находим токи и напряжения докоммутационного режима для момента времени t = (0–). Так как сопротивление индуктивности постоянному току равно нулю, а емкости – бесконечности, то расчетная схема будет выглядеть так, как это изображено на рис. 2. Индуктивность закорочена, ветвь с емкостью исключена. Так как в схеме только одна ветвь, то ток i_>1>(0–) равен току i_>3>(0–), ток i_>2>(0–) равен нулю, и в схеме всего один контур.

Составляем уравнение по второму закону Кирхгофа для этого контура:

откуда

= 4 А.

Напряжение на емкости равно нулю [u_>C>(0–) = 0].

2. Определим токи и напряжения непосредственно после коммутации для момента времени t = 0+. Расчетная схема приведена на рис. 3. По первому закону коммутации i_>L>(0–) = i_>L>(0+), т.е. ток i_>3>(0+) = 4 А. По второму закону коммутации u_>C>(0–) = u_>C>(0+) = 0.

Для контура, образованного ЭДС Е, сопротивлением R_>2> и емкостью С, согласно второго закона Кирхгофа имеем:

или

;

i_>1>(0+) = i_>2>(0+) + i_>3>(0+) = 14 А.

Напряжение на сопротивлении R_>2> равно Е – u_>C>(0+) = 100 В, напряжение на индуктивности равно напряжению на емкости.

3. Рассчитываем принужденные составляющие токов и напряжений для . Как и для докоммутационного режима индуктивность закорачивается, ветвь с емкостью исключается. Схема приведена на рис. 4. и аналогична схеме для расчета параметров докоммутационого режима.

= 10 А;

= 100 В; ;

4. Определяем свободные составляющие токов и напряжений для момента времени t = 0+, исходя из выражений i(0+) = i_>пр>(0+) + i_>св>(0+) и u(0+) = u_>пр>(0+) + u_>св>(0+).

i_>св1>(0+) = 4 А; i_>св2>(0+) = 10 А; i_>св3>(0+) = –6 А; u_>св>_>L>(0+) = u_>свС>(0+) = 0; .

5. Определяем производные свободных токов и напряжений в момент времени непосредственно после коммутации (t = 0+), для чего составим систему уравнений, используя законы Кирхгофа для схемы, изображенной на рис. 3, положив Е = 0.

;

(2)

Производную тока через индуктивность можно найти, используя выражение: , а производную напряжения на емкости – из уравнения . Т.е.

и ,

откуда

; (3)

Подставляя (3) в (2), после решения получаем:

; ; ;

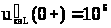Все полученные результаты заносим в таблицу.

	i_>1>	i_>2>	i_>3>	u_>L>	u_>C>	u_>R2>
t = 0+	14	10	4	0	0	100
	10	0	10	0	0	100
	4	10	–6	0	0	0
	–10⁵	–10⁵	0	10⁶	10⁶	–10⁶

6. Составляем характеристическое уравнение. Для этого исключим в послекоммутационной схеме источник ЭДС, разорвем любую ветвь и относительно разрыва запишем входное сопротивление для синусоидального тока . Например, разорвем ветвь с сопротивлением R_>2>: