Алгебра матриц
Алгебра матриц
Основные понятия
Определение.
Прямоугольная таблица из m
строк и n
столбцов, заполненная некоторыми
математическими объектами, называется
 – матрицей.
– матрицей.
Мы будем рассматривать числовые матрицы. Числа, составляющие матрицу, называются ее элементами. Для обозначения матрицы, как правило, используются круглые скобки. При записи, в общем виде элементы матрицы обозначаются одной буквой с двумя индексами, из которых первый указывает номер строки, а второй – номер столбца матрицы. Например, матрица

.
.
В сокращенной записи: А=(а>ij>); где а>ij> - действительные числа, i=1,2,…m;
j=1,2,…,n
(кратко
 ,
,
 .
). Произведение
.
). Произведение
 называют размером матрицы.
называют размером матрицы.
Матрица называется квадратной порядка n, если число ее строк равно числу столбцов и равно n:

Упорядоченный набор
элементов а>11>,а>22>,…,а>nn>
называется главной диагональю, в свою
очередь, а>1>>n>,а>2,>>n>>-1>,…,а>n>>1
>– побочной
диагональю матрицы. Квадратная матрица,
элементы которой удовлетворяют условию:

называется диагональной, т.е. диагональная матрица имеет вид:

Диагональная матрица порядка n называется единичной, если все элементы ее главной диагонали равны 1. Матрица любого размера называется нулевой или нуль матрицей, если все ее элементы равны нулю. Единичная матрица обозначается буквой Е, нулевая – О. Матрицы имеют вид:

.

Линейные операции над матрицами
Определение. Суммой
матриц А=(а>ij>)
и B=(b>ij>)
одинаковых размеров
 называется матрица С=(с>ij>)
тех же размеров, такая что c>ij>=a>ij>+b>ij>
для всех i
и j.
называется матрица С=(с>ij>)
тех же размеров, такая что c>ij>=a>ij>+b>ij>
для всех i
и j.
 .
.
Таким образом, чтобы сложить матрицы А и В, надо сложить их элементы, стоящие на одинаковых местах. Например,
A
+ B
=
 = C
= C
Определение. Произведение матрицы А на число называется матрица А=( а>ij>), получаемая умножением всех элементов матрицы А на число .

Например, если
 и =5,
то
и =5,
то

Разность матриц А и В можно определить равенством А-В=А+(-1)В.
Рассмотренные операции называются линейными.
Отметим некоторые свойства операций.
Пусть А,В,С – матрицы одинакового размера; , - действительные числа.
А+В = В+А – коммутативность сложения.
(А+В)+С = А+(В+С) – ассоциативность сложения.
Матрица О, состоящая из нулей, играет роль нуля: А+О=А.
Для любой матицы А существует противоположная –А, элементы которой отличаются от элементов А знаком, при этом А+( -А)=О.
(А) = ()А = (А). 6. (+)А = А+А.
7. (А+В) = А+В. 8. 1* А = А. 9. 0 * А = 0.
Умножение матриц
В матричной алгебре важную роль играет операция умножения матриц, это весьма своеобразная операция.
Определение.
Произведением матрицы А=(а>ij>)
размера
 и прямоугольной матрицы B=(b>ij>)
размера
и прямоугольной матрицы B=(b>ij>)
размера
 называется прямоугольная матрица
С=(с>ij>)
размера
называется прямоугольная матрица
С=(с>ij>)
размера
 ,
такая что c>ij>=a>i>>1>+b>1>>j>+
a>i>>2>+b>2>>j>+…+
a>ik>+b>kj>;
,
такая что c>ij>=a>i>>1>+b>1>>j>+
a>i>>2>+b>2>>j>+…+
a>ik>+b>kj>;
 ,
,
 .
.
Таким образом, элемент произведения матриц А и В, стоящий в i-ой строке и j-ом столбце, равен сумме произведений элементов i-ой строки первой матрицы А на соответствующие элементы j-ого столбца второй матрицы В т.е.
 .
.
П роизведение
С=АВ определено, если число столбцов
матрицы А равно числу строк матрицы В.
Это условие, а также размеры матриц
можно представить схемой:
роизведение
С=АВ определено, если число столбцов
матрицы А равно числу строк матрицы В.
Это условие, а также размеры матриц
можно представить схемой:

 Очевидно,
что операция умножения квадратных
матриц всегда определена.
Очевидно,
что операция умножения квадратных
матриц всегда определена.
Примеры. Найдем произведения матриц АВ и ВА, если они существуют.
1.
 ,
,
 .
.



2.
 ,
,
 .
.



Таким образом,
коммутативный (переместительный) закон
умножения матриц, вообще говоря, не
выполняется, т.е.
 В частном случае коммутативным законом
обладает произведение любой квадратной
матрицы А n-го
порядка на единичную матрицу Е такого
же порядка, т.е.
В частном случае коммутативным законом
обладает произведение любой квадратной
матрицы А n-го
порядка на единичную матрицу Е такого
же порядка, т.е.

3.
 ,
,
 .
.
Для этих матриц произведение как АВ ,так и ВА не существует.
 ,
,


Получим
 ,
ВА – не существует.
,
ВА – не существует.
Свойства умножения матриц.
Пусть А,В,С – матрицы соответствующих размеров (т.е. произведения матриц определены), - действительное число. Тогда на основании определений операций и свойств действительных чисел имеют место следующие свойства:
(АВ)С = А(ВС) – ассоциативность.
(А+В)С = АС+ВС – дистрибутивность.
А(В+С) = АВ+АС – дистрибутивность.
(АВ) = (А)В = А(В).
ЕА = АЕ = А, для квадратных матриц единичная матрица Е играет роль единицы.
Приведем пример доказательства лишь одного свойства. Докажем, например, свойство 3.
Пусть для А=(а>ij>), B=(b>ij>), C=(c>ij>) произведения матриц определены. Найдем элемент i-ой строки и j-го столбца матрицы А(В+С). Это будет число
а>i>>1>(b>1>>j>+c>1>>j>)+ а>i>>2>(b>2>>j>+c>2>>j>)+…+а>in>(b>nj>+c>nj>) =
(а>i>>1>b>1>>j>+a>i>>2>b>2>>j>+…+a>in>b>nj>)+ (а>i>>1>c>1>>j>+a>i>>2>c>2>>j>+…+a>in>c>nj>).
Первая сумма в правой части равенства равна элементу из i-ой строки и j-го столбца матрицы АВ, а вторая сумма равна элементу из i-ой строки и j-го столбца матрицы АС. Рассуждение верно при любых i и j, то свойство 3 доказано.
Упражнение 1. Проверьте свойство ассоциативности 1 для матриц:
 ,
,
 ,
,
 .
.
Упражнение 2. Проверьте свойство дистрибутивности 2 для матриц:
 ,
,
 ,
,
 .
.
Упражнение 3. Найти
матрицу А3,
если
 .
.
Вырожденные и невырожденные матрицы
Определение. Матрица называется вырожденной, если ее определитель равен нулю, и невырожденной, если определитель матрицы отличен от нуля.
Пример.
 ,
,
 = 16-15 = 1
= 16-15 = 1
 0; А – невырожденная матрица.
0; А – невырожденная матрица.
 ,
,
 = 12-12 = 0; А – вырожденная матрица.
= 12-12 = 0; А – вырожденная матрица.
Теорема. Произведение матриц есть вырожденная матрица тогда и только тогда, когда хотя бы один из множителей есть вырожденная матрица.
Необходимость. Пусть
АВ – вырожденная матрица, т.е.
 =0.
Тогда, в силу того, что определитель
произведения матриц равен произведению
определителей перемножаемых матриц,
имеем
=0.
Тогда, в силу того, что определитель
произведения матриц равен произведению
определителей перемножаемых матриц,
имеем
 Это значит, что хотя бы одна из матриц
А или В является вырожденной.
Это значит, что хотя бы одна из матриц
А или В является вырожденной.
Достаточность. Пусть
в произведении АВ матрица А вырожденная,
т.е.
 =0.
Найдем
=0.
Найдем
 ,
т.к.
,
т.к.
 =0;
итак,
=0;
итак,
 =0;
АВ - вырожденная матрица.
=0;
АВ - вырожденная матрица.
Замечание. Доказанная теорема справедлива для любого числа множителей.
Обратная матрица
Определение. Квадратная матрица В называется обратной по отношению к матрице А такого же размера, если
АВ = ВА = Е. (1)
Пример.
 ,
,
 .
.


В – матрица обратная к А.
Теорема. Если для данной матрицы обратная существует, то она определяется однозначно.
Предположим, что для матрицы А существуют матрицы Х и У, такие, что
АХ = ХА = Е (2)
АУ = УА = Е (3)
Умножая одно из равенств, например, АХ = Е слева на У, получим У(АХ) = УЕ. В силу ассоциативности умножения имеем (УА)Х = УЕ. Поскольку УА = Е, то ЕХ = УЕ, т.е. Х = У. Теорема доказана.
Теорема (необходимое и достаточное условие существования обратной матрицы).
Обратная матрица А-1 существует тогда и только тогда, когда исходная матрица А невырожденная.
Необходимость. Пусть
для матрицы А существует обратная А-1,
т.е. А
 А-1
= А-1
А-1
= А-1 А
= Е. Тогда, А
А
= Е. Тогда, А А-1=
А
А-1=
А А-1=Е=1,
т.е. А
А-1=Е=1,
т.е. А 0
и А-1
0
и А-1 0;
А – невырожденная.
0;
А – невырожденная.
Достаточность. Пусть дана невырожденная матрица порядка n
 ,
,
так что ее определитель
 0.
Рассмотри матрицу, составленную из
алгебраических дополнений к элементам
матрицы А:
0.
Рассмотри матрицу, составленную из
алгебраических дополнений к элементам
матрицы А:
 ,
,
ее называют присоединенной к матрице А.
Следует обратить
внимание на то, что алгебраические
дополнения к элементам i-ой
строки матрицы А стоят в i-ом
столбце матрицы А*,
для
 .
.
Н
 айдем
произведения матриц АА*
и А*А.
Обозначим АА*
через С, тогда по определению произведения
матриц имеем: С>ij>>
>= а>i>>1>А>
1>>j>
+ а> >>i>>2>А>
2>>j>
+ … + а>
>>in>А>nj>;
= 1, n:
j
= 1, n.
айдем
произведения матриц АА*
и А*А.
Обозначим АА*
через С, тогда по определению произведения
матриц имеем: С>ij>>
>= а>i>>1>А>
1>>j>
+ а> >>i>>2>А>
2>>j>
+ … + а>
>>in>А>nj>;
= 1, n:
j
= 1, n.
При
= j
получим сумму произведений элементов
- ой строки на алгебраические дополнения
этой же строки, такая сумма равняется
значению определителя. Таким образом
С>ij>>
>= |А| =
- это элементы главной диагонали матрицы
С. При
 j,
т.е. для элементов С>ij>>
>вне
главной диагонали матрицы С, имеем сумму
произведений всех элементов некоторой
строки на алгебраические дополнения
другой строки, такая сумма равняется
нулю. Итак,
j,
т.е. для элементов С>ij>>
>вне
главной диагонали матрицы С, имеем сумму
произведений всех элементов некоторой
строки на алгебраические дополнения
другой строки, такая сумма равняется
нулю. Итак,
 = АА*
= АА*
Аналогично доказывается, что произведение А на А* равно той же матрице С. Таким образом, имеем А*А = АА* = С. Отсюда следует, что

Поэтому, если в
качестве обратной матрицы взять
 ,
то
,
то
 Итак, обратная матрица существует и
имеет вид:
Итак, обратная матрица существует и
имеет вид:
 .
.
Пример. Найдем матрицу, обратную к данной:

Находим
= |А| = -1
0, А существует. Далее находим алгебраические
дополнения элементов матрицы А:
существует. Далее находим алгебраические
дополнения элементов матрицы А:
А =
=
 = 0 ; А
= 0 ; А =
=
 = -1; А
= -1; А =
=
 = 3;
= 3;
А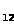 =
=
 = -3; А
= -3; А =
=
 = 3; А
= 3; А =
=
 = -4;
= -4;
А =
=
 = 1; А
= 1; А =
=
 = -1; А
= -1; А =
=
 = 1;
= 1;
А =
=

Список литературы
Для подготовки данной применялись материалы сети Интернет из общего доступа