Симметpия относительно окpужности
Симметpия относительно окpужности
С.А. Ануфриенко
Симметpия, как бы шиpоко или узко мы ни понимали это слово, есть идея, с помощью котоpой человек в течение веков пытался объяснить и создать поpядок, кpасоту и совеpшенство.
Геpман Вейль
Введение
Со временем замечаешь, как непохожи друг на друга пути, ведущие к решению красивых геометрических проблем. Бесконечность возможных направлений поиска многих людей приводит в трепет, но одновременно дает хорошую надежду отыскать свою собственную дорогу в геометрическом лабиринте. В любом случае открытие метода, позволяющего решить целый ряд сложных задач, является событием большой редкости. Об одном из таких методов и пойдет речь в этой статье. Мы начинаем с перечисления некоторых классических проблем, решения которых будут приведены позже.
A. Четыре окружности >1>, >2>, >3> и >4> расположены таким образом, что >i> касается >i+1> для i < 4, а >4> касается >1>. Образуются четыре точки касания. Доказать, что найдется окружность, проходящая через все эти точки.
B. Разделить с помощью циркуля данный отрезок [AB] на n равных частей (n N).
C. Только с помощью циркуля найти центр данной окружности.
D. Даны точки A, B, C, D и окружность . Только с помощью циркуля найти пересечение прямых (AB) и (CD), а также точки пересечения прямой (AB) с окружностью (задачи геометрии Мора-Маскерони).
E. Построить окружность, которая проходит через две данные точки A и B и касается данной окружности >1>.
F. Построить окружность, проходящую через данную точку и касающуюся двух данных окружностей.
G. Построить окружность, касающуюся трех данных окружностей (задача Аполлония).
H. Для двух различных точек A и B и положительного числа k найти геометрическое место точек X, для которых отношение XA/XB равно k 1 (окружность Аполлония).
I. Для произвольного треугольника через r, R и d обозначим соответственно радиусы вписанной и описанной окружностей и расстояние между их центрами. Доказать, что d2 = R2-2Rr (формула Эйлера).
Инверсия и ее свойства
В 1831 году Л. Дж Магнус впервые стал рассматривать преобразование плоскости, которое получило название симметрии относительно окружности или инверсии (от лат. inversio - обращение). Под инверсией плоскости относительно окружности (O,R) с центром в точке O и радиусом R понимают такое преобразование множества \{O}, при котором каждой точке A \{O} ставится в соответствие такая точка A, что A лежит на луче [OA) и OA·OA = R2 (далее будем использовать обозначение inv>O>R(A) = A). Заметим сразу, что инверсия не определена в точке O, но иногда бывает полезно добавить к плоскости одну бесконечно удаленную точку, т.е. рассмотреть множество {} и при этом считать, что inv>O>R(O) = и inv>O>R() = O.
На рис. 1 указан способ построения образа точки A при инверсии относительно окружности = (O,R). Для этого проводят перпендикуляр (AB) к прямой (OA) и из точки пересечения (AB) проводят касательную к окружности . Из подобия треугольников OAB и OBA получаем отношение OA/ OB = OB/ OA или
OA·OA = OB2 = R2. Следовательно inv>O>R(A) = A.
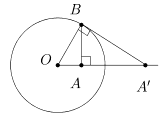
Рис. 1
На рис. 2 построение образа выполнено только с помощью циркуля (в предположении, что OA > R/2). Для этого достаточно провести окружность
(A,OA) и для двух точек пересечения (O,R)(A,OA) построить равные окружности (B,R) и (C,R). Вторая точка пересечения (B,R)(C,R), отличная от точки O, является искомой. Для доказательства используем подобие равнобедренных треугольников OBA и OBA. Сначала получаем OA/ OB = OB/OA, а затем, необходимое OA·OA = OB2 = R2. Если же OA R/2, то сначала увеличивают отрезок [OA] в n раз до отрезка [OB] (удвоение отрезка показано на рис. 3 - последовательно откладывают радиус OA на окружности (A,OA) и используют свойство правильного вписанного шестиугольника), после этого находят B = inv>O>R(B) и снова увеличивают (а не уменьшают!) отрезок [OB] в n раз до отрезка [OC]. Можно доказать, что C = inv>O>R(A).
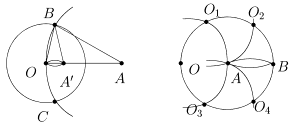
Рис. 2 Рис. 3
Из многочисленных свойств инверсии рассмотрим лишь следующие. Пусть
A = inv>O>R(A) и B = inv>O>R(B).
I. Если A B, то A B.
Утверждение требует проверки только когда лучи [OA) и [OB) совпадают. В этом случае OA OB и поэтому OA OB. Приходим к неравенству A B.
II. Все точки окружности (O,R) при инверсии inv>O>R остаются неподвижными. Внутренние точки круга с границей (O,R) переходят во внешние, а внешние - во внутренние.
Первая часть утверждения очевидна, а вторая следует из замечания: если
OA < R, то OA = R2/OA > R.
III. Если A = inv>O>R(A), то A = inv>O>R(A). Для произвольных фигур и из условия = inv>O>R() также следует = inv>O>R().
IV. Треугольники AOB и AOB подобны. При этом OBA = OAB.
Достаточно заметить, что эти треугольники имеют общий угол, а из равенства OA·OA = R2 = OB·OB следует равенство отношений OA/OB = OB/OA. Обратите внимание, что в отличие от подобия, пропорциональность связывает стороны [OA] и [OB], [OB] и [OA], а не [OA] и [OA], [OB] и [OB]. Из подобия получаем OBA = OAB.
V.
AB = AB
OA·OB ·R2.
Действительно, по свойству IV имеем
AB = AB·OA
OB = AB
OA·OB ·R2.
VI. Прямая a, проходящая через центр инверсии, отображается в себя. Если же O a и A - основание перпендикуляра из точки O на прямую a (рис. 4), то образом прямой a будет окружность >1>, построенная на отрезке [OA] как на диаметре (A = inv>O>R(A)).

Рис. 4
Для доказательства этого свойства рассмотрим произвольную точку B прямой a. По свойству IV OBA = OAB = 90. Следовательно точка B лежит на окружности с диаметром [OA]. Удивление от такого неожиданного действия инверсии на произвольную прямую пройдет, если принять в расчет бесконечно удаленную точку. Каждая прямая проходит через . Поэтому переход в точку O заставляет концы прямой сжиматься к точке O. Следующее свойство позволяет определить центр окружности, которая является образом прямой из свойства VI.
VII. Пусть >1> = inv>O>R(a). Обозначим через O>1> = S>a>(O), где S>a> - осевая симметрия с осью a (рис. 4). Тогда центром окружности >1> является точка O>1> = inv>O>R(O>1>).
Сохраняя принятые в предыдущем свойстве обозначения, имеем OO>1> = 2OA. Подставляя это в равенство OA·OA = R2 = OO>1>·OO>1> получаем OO>1> = OA/2. Поэтому точка O>1> является серединой отрезка [OA].
VIII. Окружность >1>(O>1>,r), проходящая через центр инверсии, отображается на некоторую прямую a. Более того, если A - конец диаметра, проходящего через O и O>1> (A O), то прямая a проходит через точку A = inv>O>R(A) и перпендикулярна прямой (OO>1>).
Справедливость этого свойства сразу следует из свойств III и VI.
IX. Окружность >1>(O>1>,r>1>), не проходящая через центр инверсии, отображается при inv>O>R на некоторую окружность >2>(O>2>,r>2>). Точнее, если точки A и B являются концами диаметра, лежащего на прямой (OO>1>) (рис. 5), то отрезок [AB] является диаметром окружности >2> (A = inv>O>R(A), B = inv>O>R(B)).

Рис. 5
Для доказательства рассмотрим произвольную точку C окружности >1> и покажем, что C = inv>O>R(C) >2>. Из свойства IV имеем равенства OCA = OAC и OCB = OBC. Поэтому ACB = OBC- OAC = OCB-OCA = 90. Следовательно C >2>.
Переходит ли центр O>1> в центр образа >2>, точку O>2>? Никогда (убедитесь в этом с помощью прямых вычислений, т.е. докажите, что O>1> = inv>O>R(O>1>) не может быть серединой [AB]). Этот "недостаток" инверсии с лихвой компенсируется замечательным ее свойством сохранять величину угла. Напомним, что угол между пересекающимися окружностями по определению равен углу между касательными к этим окружностям в точке их пересечения. Аналогично определяется и угол между пересекающимися прямой и окружностью. Рассмотрим частный случай: для двух касающихся окружностей >1> и >2> определим величину угла между inv>O>R(>1>) и inv>O>R(>2>). Вид образов inv>O>R(>1>) и inv>O>R(>2>) во многом зависит от положения точки O относительно окружностей >1> и >2>. Так, если O >1>>2>, то из свойств I и IX получаем, что inv>O>R(>1>) и inv>O>R(>2>) являются касающимися окружностями. Если же O лежит только на одной из окружностей, например на >1>, то из свойств I, VIII и IX получим касающиеся прямую inv>O>R(>1>) и окружность inv>O>R(>2>). И, наконец, если O совпадает с точкой касания окружностей, то inv>O>R(>1>) и inv>O>R(>2>) являются параллельными прямыми (величина угла между параллельными прямыми по определению равна нулю). Итак, в каждом из случаев, величина угла между inv>O>R(>1>) и inv>O>R(>2>) равна нулю. Аналогично можно установить, что если прямые a и b параллельны, то величина угла между inv>O>R(a) и inv>O>R(b) также равна нулю.
X. Инверсия сохраняет величину угла между прямыми, пересекающимися окружностями, пересекающимися прямой и окружностью.
Докажем сначала, что для любых прямых угол a,b совпадает с углом между inv>O>R(a) и inv>O>R(b). Утверждение очевидно, если прямые проходят через точку O. Пусть теперь O a и O b (рис. 6). Обозначим через >1> окружность, в которую переходит прямая b, и через b>1> - касательную к >1> в точке O. Так прямые b и b>1> перпендикулярны одному и тому же диаметру, то они параллельны. Поэтому угол между a и >1>, равный по определению углу между a и b>1>, совпадает с углом a,b. Рассуждения аналогичны и в случае, когда O ab (надо рассмотреть касательные к окружностям inv>O>R(a) и inv>O>R(b) в точке O).

Рис. 6
Поскольку угол между окружностями и между прямой и окружностью определялся через касательные, то доказательство остальных двух утверждений легко сводятся к случаю сохранения угла между прямыми.
Основой решения целого ряда геометрических проблем является удачное применение того или иного преобразования плоскости. При этом мы считаем использование какого-либо преобразования удачным, если образы рассматриваемых фигур поддаются простому геометрическому анализу. В задаче Фаньяно1, например, стороны треугольника наименьшего периметра получаются из отрезка прямой серией осевых симметрий. При отыскании точки Ферма2 похожая идея реализуется с помощью поворота на 60. В следующих параграфах попробуем выяснить насколько способность к упрощению свойственна инверсии. Этот параграф закончим решением проблемы A.
Решение A. Обозначим через A, B, C, и D соответственно точки касания >1>>2>, >2>>3>, >3>>4> и >4>>1>. Сделаем инверсию с центром в O = A относительно окружности некоторого радиуса R. По свойству VIII и IX получим пару параллельных прямых a = inv>O>R(>1>), b = inv>O>R(>2>) и пару касающихся окружностей >3> = inv>O>R(>3>) и >4> = inv>O>R(>4>) (рис. 7).

Рис. 7
Нетрудно заметить, что точки касания исходных окружностей, за исключением точки A (которую инверсия забросит в бесконечность), отобразятся в точки касания образов. Докажем теперь, что B, C и D лежат на одной прямой. Так как (KB)(LD), то BKC = CLD. Отсюда следует равенство KCB = LCD (KCB и LCD являются равнобедренными), поэтому B, C и D лежат на одной прямой. Обозначим эту прямую через c и подействуем на нее снова инверсией inv>O>R. Ее образ - это окружность inv>O>R(c), которая проходит через центр инверсии, точку A, а также через точки B = inv>O>R(B), C = inv>O>R(C) и D = inv>O>R(D).
Геометрия Мора-Маскерони
Теория построения одним циркулем получила свою известность благодаря книге "Геометрия циркуля"(1797 г.) Лоренцо Маскерони3. Значительно позже в одном из букинистических магазинов была обнаружена книга датского математика Георга Мора "Датский Евклид", датированная 1672 годом! Обе книги содержат основной результат геометрии циркуля:
Теорема Мора-Маскерони. Все построения, выполненные с помощь циркуля и линейки, могут быть проделаны только с помощью циркуля (при этом мы считаем прямую построенной, если найдены хотя бы две точки этой прямой).
Для доказательства этой теоремы достаточно научиться находить только с помощью циркуля пересечения двух прямых, прямой и окружности, что и составляет проблему D. Сначала рассмотрим решения задач B и C, которые носят вспомогательный характер.
Решение B. Чтобы разделить отрезок [AB] на n равных частей, сначала увеличим его в n раз, т.е. найдем точку C, что AC = nAB. А затем построим точку C - образ точки C при инверсии относительно окружности (A,AB). Из соотношения AC·AC = AB2 получаем AC = AB/n. Все указанные построения можно выполнить только с помощью циркуля (для этого даже не нужна прямая (AB)).
Решение C. Выберем произвольную точку O окружности >1>(X,r), центр X которой нам нужно определить (рис. 8).

Рис. 8
Из точки O проведем произвольную окружность (O,R) так, чтобы она пересекала исходную окружность >1>. Обозначим точки пересечения >1> через A и B. Куда перейдет прямая (AB) при инверсии inv>O>R? Конечно же в >1>, поскольку точки A и B остаются неподвижными (свойства II и VI). По свойству VII центр inv>O>R((AB)) (т.е. центр >1>) является образом точки S>(AB)>(O) при inv>O>R. Из этих рассуждений следует цепочка необходимых построений. Сначала находим точку O>1> = S>(AB)>(O), симметричную O относительно прямой (AB) (школьная задача). А затем строим образ точки O>1> при inv>O>R, он и будет искомым центром. Все указанные построения выполняются только с помощью циркуля.
Решение D. Опишем поиск пересечения двух прямых только с помощью циркуля. Пусть даны точки A, B, C и D (рис. 9).

Рис. 9
Выберем точку O так, чтобы она не лежала на прямых a = (AB) и b = (CD). При инверсии inv>O>R прямые a и b должны перейти в окружности inv>O>R(a) и inv>O>R(b), а их точка пересечения отобразится в точку пересечения окружностей inv>O>R(a) и inv>O>R(b), отличную от точки O (свойства VI и I). Теперь необходимые построения становятся очевидными: с помощью свойства VII строим окружности inv>O>R(a) и inv>O>R(b), находим точку пересечения этих окружностей - точку X, и снова действуем инверсией уже на точку X. Точка Y = inv>O>R(X) является искомой. Пересечение прямой и окружности находится похожим образом.
Теперь терема Мора-Маскерони следует из решений задач B, C и D.
Задача Аполлония
В этом параграфе рассмотрим задачу о построении окружности, касающейся трех данных окружностей, названную в честь крупнейшего специалиста по коническим сечениям древности Аполлония Пергского4. Решению проблемы G предшествуют решения задач E и F.
Решение E. Чтобы построить окружность >2>, проходящую через точки A и B и касающуюся данной окружности >1>, рассмотрим инверсию с центром в точке O = A относительно окружности произвольного радиуса R. Образом >2> при инверсии inv>O>R должна быть некоторая прямая a, проходящая через точку B = inv>O>R(B) и касающаяся окружности inv>O>R(>1>) (свойства VIII и IX). Касательные из произвольной точки X к произвольной окружности (Y,r) провести довольно легко: для этого достаточно построить вспомогательную окружность на диаметре [XY] и соединить X с точками пересечения . Теперь выполняем необходимые построения в следующем порядке: находим B = inv>O>R(B) и inv>O>R(>1>), через точку B проводим касательные a и b к окружности inv>O>R(>1>), строим образы inv>O>R(a) и inv>O>R(b) при инверсии inv>O>R. В зависимости от расположения точки B относительно окружности inv>O>R(>1>) может быть два, одно и ни одного решения (например, когда B находится внутри inv>O>R(>1>)).
Решение F. Для решения этой задачи достаточно уметь проводить общую касательную к двум произвольным окружностям (X,r) и (Y,R). Будем считать, что r < R. Проведем из точки X касательную a к окружности >1>(Y,R-r) (рис. 10), тогда искомая внешняя касательная b к окружностям и будет параллельна прямой a и находится от нее на расстоянии r.

Рис. 10
Для проведения внутренней касательной вместо >1>(Y,R-r) надо рассмотреть окружность >2>(Y,R+r). В общем случае возможно до четырех решений. Теперь вернемся к исходной задаче. Пусть даны точка A и две окружности >1> и >2>. Искомая окружность , проходящая через A и касающаяся >1> и >2>, при инверсии с центром O = A должна перейти в некоторую прямую a, которая касается окружностей inv>O>R(>1>) и inv>O>R(>2>) (свойства VIII и IX). Таким образом, приходим к следующему порядку построений: находим inv>O>R(>1>) и inv>O>R(>2>), проводим общие касательные (a,b,c,d) и строим образы этих касательных при inv>O>R. В общем случае получится до четырех искомых окружностей, однако в одном случае решений будет бесконечно много (представьте, что произойдет после инверсии с окружностями >1> и >2>, если они касаются в точке A).
Решение G. Задача Аполлония легко сводится к предыдущей задаче. Пусть даны окружности >1>(O>1>,r>1>), >2>(O>2>,r>2>) и >3>(O>3>,r>3>), и r>1> < r>2> < r>3>. Построим окружность (O,R), проходящую через точку O>1> и касающуюся окружностей
>2>(O>2>,r>2>-r>1>) и >3>(O>3>,r>3>-r>1>). Уменьшив радиус окружности на r>1>, т.е. рассматривая (O,R-r>1>), приходим к одной из искомых окружностей. Количество решений исследовать самим (кажется, исключая бесконечный случай, возможно до восьми решений).
Изменение расстояния при инверсии
Основой исследований в этом параграфе будет формула V для вычисления расстояния между образами точек A и B при инверсии относительно (O,R): AB = ABR2/(OA·OB). Из этой формулы сразу видно, что расстояние при инверсии для произвольных точек A и B не сохраняется и искажение расстояния происходит сильнее при приближении точек A и B к центру окружности инверсии. Прежде чем установить менее очевидный факт, введем важное в теории круговых преобразований5 понятие двойного отношения четырех точек.
Определение. Двойным отношением четырех точек A, B, C и D называют число
AC
BC : AD
BD .
Теорема. Двойное отношение четырех точек сохраняется при инверсии.
Доказательство. Обозначим через A, B, C и D соответственно образы точек A, B, C и D при инверсии относительно окружности (O,R). Тогда из формулы V имеем
AC
BC : AD
BD = AC/(OA·OC)
BC/OB·OC : AD/(OA·OD)
BD/(OB·OD) =
= AC
BC : AD
BD .
Следующая теорема является решением проблемы H.
Теорема. Пусть даны точки A, B и число k > 0 (k 1). Множество состоит из всех таких точек X плоскости, для которых XA:XB = k. Тогда является окружностью (окружность Аполлония), центр которой лежит на прямой (AB).
Доказательство. На прямой (AB) можно легко найти две точки O и C, принадлежащие множеству (одна из них будет внутренней точкой отрезка [AB], другая - внешней точкой этого отрезка). Рассмотрим инверсию относительно окружности с центром в точке O произвольного радиуса R. Для образов точек A, B и C имеем
CA
CB = CAR2/(OC·OA)
CBR2/(OC·OB) = CA
CB : OA
OB = k:k = 1. 1
Пусть X = inv>O>R(X) и = inv>O>R(). Тогда, учитывая (1) и сохранение при инверсии отношения четырех точек, получаем
X XA
XB : CA
CB = k:k = 1
XA
XB : CA
CB = 1 XA
XB = 1.
Последнее означает, что - серединный перпендикуляр к отрезку [AB]. Отсюда = inv>O>R() - окружность, диаметр которой лежит на прямой (AB).
Формула следующей теоремы, названная в честь Леонарда Эйлера6, связывает между собой радиусы вписанной и описанной окружностей произвольного треугольника с расстоянием между их центрами.
Теорема. Пусть для произвольного треугольника ABC числа r, R и d соответственно обозначают радиусы вписанной и описанной окружностей и расстояние между их центрами. Тогда d2 = R2-2Rr.
Доказательство. Точки касания вписанной окружности (O,r) со сторонами [AB], [AC] и [BC] обозначим соответственно через K, L и M (рис. 11).

Рис. 11
Пусть также >1>(O>1>,R) - описанная около треугольника ABC окружность. Рассмотрим инверсию относительно вписанной окружности (O,r). Так как прямые (AK) и (AL) являются касательными к окружности инверсии, образом точки A будет середина отрезка [KL] (точка A), аналогично B = inv>O>r (B) - середина [KM] и C = inv>O>r (C) - середина [LM]. Образом окружности >1>(O>1>,R) будет окружность >1>, проходящая через точки A,B,C и имеющая радиус равный r/2 (так как при гомотетии H>O>-1/2 окружность переходит в окружность, проходящую через середины сторон KLM, т.е. в >1>). Теперь попробуем выяснить, как вообще изменяется радиус окружности при инверсии. Обозначим через X и Y точки диаметра окружности >1>(O>1>,R), лежащие на прямой (OO>1>) (рис. 12).

Рис. 12
По свойству IX отрезок [inv>O>r(X) inv>O>r (Y)] является диаметром окружности
inv>O>r (>1>), а по свойству V его длина равна
XY = XY
OX·OY ·r2 = 2Rr2
R-d·R+d = 2Rr2
R2-d2 .
Учитывая, что XY = 2R, где R - радиус окружности inv>O>r(>1>), получаем формулу
R = Rr2
R2-d2 .
Возвращаясь к образу описанной окружности при инверсии относительно (O,r), имеем
r
2 = Rr2
R2-d2 R2-d2 = 2Rrd2 = R2-2Rr.
Закончим этот параграф одним совершенно неожиданным результатом. Сначала напомним некоторые определения и факты. Окружностью Эйлера треугольника ABC называется окружность, проходящая через середины его сторон. На этой окружности также лежат основания высот ABC и середины трех отрезков, соединяющих ортоцентр этого треугольника (т.е. точку пересечения его высот или их продолжений7) с вершинами. Поскольку на окружности Эйлера лежат девять точек, естественно связанных с треугольником ABC, ее называют еще окружностью девяти точек. Вневписанной окружностью треугольника ABC называется окружность, касающаяся стороны этого треугольника и продолжений двух других его сторон. В следующей лемме перечисляются некоторые свойства вневписанной окружности.
Лемма 1. Пусть AB = c, AC = b, BC = a, p - полупериметр ABC, O>1> и O>a> - центры вписанной (>1>) и вневписанной (>a>) окружностей (рис. 13), r>1> и r>a> - их радиусы, X и X>a> - точки касания этих окружностей со стороной [BC], K и L - с прямой (AC), M и N - с прямой (AB). Пусть также (B>1>C>1>) - общая внутренняя касательная к >1> и >a>, отличная от (BC). Тогда
AL = p;
AK = p-a, CK = p-c, BX = p-b;
BX = CX>a>;
BC>1> = B>1>C = b-c;
pr>1> = r>a>(p-a);
r>1>r>a> = (p-b)(p-c).

Рис. 13
Доказательство. 1) Следует из 2AL = AL+AN = (AC+CX>a>)+(AB+BX>a>) = 2p.
2) Первое равенство получается из 2AK = AK+AM = (AC-CX)+(AB-BX) = 2p-2a. Остальные доказываются аналогично.
3) Из 2) и 1) имеем BX = p-b = AL-AC = CL = CX>a>.
4) При симметрии относительно биссектрисы [AO>a>) угла BAC окружности >1> и >a> остаются неподвижными и отрезок [BC] одной внутренней касательной переходит в отрезок [B>1>C>1>] другой внутренней касательной. Отсюда BC>1> = B>1>C и C>1>N = CL. Из последнего равенства в предположении b > c получаем BC>1> = AN-AB-CL = p-c-(p-b) = b-c.
5) Следует из 1) и 2) и из подобия треугольников AO>1>K и AO>a>L.
6) Следует из 1) и 2) и из подобия треугольников KO>1>C и LCO>a>.
Лемма доказана.
Лемма 2. Для окружностей (O,R) и >1>(O>1>,R>1>) условие inv>O>R(>1>) = >1> выполнено тогда и только тогда, когда >1>.
Доказательство. Пусть inv>O>R(>1>) = >1>, >1> = {A,B} и >1>(OO>1>) = {X,Y}. Тогда inv>O>R(X) = Y. Отсюда OX·OY = R2 = OA2. Поэтому (OA) - касательная к окружности >1>. Что означает (OA)(O>1>A) и >1>.
Предположим теперь, что >1>. Обозначим через >2> = inv>O>R(>1>). Из свойства X получаем >2>. Поскольку существует единственная окружность, проходящая через A и B (по-прежнему, {A,B} = >1>) и перпендикулярная , >2> = >1>. Лемма доказана.
Теорема (Фейербах). Окружность Эйлера треугольника ABC касается вписанной и трех вневписанных окружностей этого треугольника.
Доказательство. Сохраним некоторые обозначения леммы 1. Середины сторон треугольника обозначим через A, B и C (рис. 14). На отрезке [XX>a>] как на диаметре построим окружность . Из леммы 1 сразу получаем, что точка A будет центром (так как BX = CX>a>), а ее радиус R = XX>a>/2 = (a-2BX)/2 = (b-c)/2 (далее предполагаем, что b c). Рассмотрим симметрию относительно . Из условий >1> и >1> и из леммы 2 заключаем, что inv>O>R(>1>) = >1> и inv>O>R(>a>) = >a>. Чтобы найти образ окружности Эйлера (>э>) при инверсии относительно введем дополнительные обозначения.

Рис. 14
Пусть S - общая точка биссектрисы [AO>a>) и прямых (BC) и (B>1>C>1>). Тогда SC = ab/(b+c) и SB = ac/(b+c). Отсюда
SA = (SC-SB)/2 = a
2 · b-c
b+c .
Пусть также точки B и C являются соответственно пересечением касательной (B>1>C>1>) с прямыми (AB) и (AC). Из подобия треугольников SAB и SBC>1> получаем
AB = BC>1>· SA
SB = (b-c)· a
2 · b-c
b+c
a· c
b+c
= (b-c)2
2c .
Поскольку AB = c/2,
AB·AB = (b-c)2/4 = R2. (1)
Рассматривая подобные треугольники ASC и CSB>1> приходим к
AC = B>1>C· SA
SC = (b-c)· a
2 · b-c
b+c
a· b
b+c
= (b-c)2
2b .
Отсюда
AC·AC = (b-c)2
2b · b
2 = R2. (2)
Равенства (1) и (2) означают, что inv>O>R(B) = B и inv>O>R(C) = C. Поэтому
inv>O>R(>э>) = (BC) = (B>1>C>1>) и >э> касается inv>O>R(>1>) = >1> и inv>O>R(>a>) = >a>. Аналогично доказывается, что >э> касается оставшихся двух вневписанных окружностей. Теорема доказана.
Нетрудно заметить, что окружность Эйлера >э> треугольника ABC является окружностью Эйлера для каждого из следующих треугольников: HAB, HAC, HBC (H - ортоцентр ABC). Каждый из этих треугольников имеет свою вписанную и три вневписанные окружности. Таким образом, теорема Фейербаха приводит к фантастическому результату: окружность Эйлера треугольника ABC касается по крайней мере шестнадцать окружностей, естественно определенных этим треугольником.
В заключение приведем небольшой список задач для самостоятельного решения. Если какая-либо задача не решается в течение 497 секунд, разрешено посмотреть указание к решению задачи.
Задачи
1. Где-то в пустыне находится лев. Требуется загнать его в круглую клетку (будьте осторожны с выбором своего местоположения).Решение
2. Пусть на плоскости дано конечное множество точек, причем прямая, проходящая через любые две точки этого множества, содержит также третью точку этого множества. Докажите, что все точки данного множества лежат на одной прямой (теорема Сильвестра).Решение
3. На плоскости дано конечное множество точек, причем никакие три из них не лежат на одной прямой, и окружность, проходящая через любые три данные точки, содержит еще одну точку этого же множества. Докажите, что тогда все данные точки лежат на одной окружности.Решение
4. Докажите, что для любых двух непересекающихся окружностей >1> и >2> найдется инверсия, которая переведет их в концентрические окружности >1> и >2>. Решение
5. Даны две непересекающиеся окружности и , причем лежит внутри . Окружность >1>, одновременно касающаяся и , обладает свойством Штейнера, если найдется такая цепочка окружностей >1>,..., >n>, касающихся и и таких, что >i> касается >i+1> для i < n и >n> касается >1>. Докажите, что если для окружностей и найдется хотя бы одна окружность, обладающая свойством Штейнера, то и любая окружность S>1>, касающаяся внутренне и внешне, обладает свойством Штейнера (поризм Штейнера). Решение
6. Вывести формулу Герона-Архимеда для вычисления площади треугольника ABC: S2>>>ABC> = p(p-a)(p-b)(p-c) (обозначения из леммы 1 последнего параграфа). Решение
7. Доказать, что точка пересечения медиан ABC, ортоцентр и центр описанной около ABC окружности лежат на одной прямой (прямая Эйлера). Решение
8. Докажите, что центр окружности Эйлера лежит на прямой Эйлера. Решение
Указания к решению задач
1. Выходя на охоту, следует вооружиться свойством II инверсии.
2. Обозначим через d>i,j,k> расстояние от точки A>i> до прямой (A>j>A>k>), проходящей через точки A>j> и A>k> данного множества. Предположим противное и, например, d>1,2,3> - минимальное ненулевое число среди d>i,j,k>. На прямой (A>2>A>3>) найдите точку A>j> и получите противоречие с минимальностью d>1,2,3>.
3. Сделайте инверсию с центром в одной из точек данного множества и воспользуйтесь свойством VIII и теоремой Сильвестра.
4. Докажите сначала (например, координатным методом), что для любых двух неконцентрических окружностей >1> и >2> геометрическим множеством точек плоскости, отрезки касательных из которых к >1> и >2> равны между собой, является прямая (радикальная ось окружностей >1> и >2>). Пусть теперь a - радикальная ось окружностей >1> и >2> с центрами O>1> и O>2> соответственно и X - точка пересечения прямых a и (O>1>O>2>). Построим окружность >3> с центром в X и радиусом равным отрезку касательной из точки X к >1>. Тогда >3>>1> и >3>>2>. Обозначим через O одну из точек пересечения >3> с (O>1>O>2>). Докажите теперь, что O - центр искомой инверсии (используйте лемму 2 и свойства VI и IX).
5. Переведите подходящей инверсией окружности и в концентрические окружности.
6. Следует перемножить три равенства: 5, 6 (лемма 1) и равенство p = p.
7. При гомотетии с центром в точке пересечения медиан и коэффициентом -1/2 ортоцентр треугольника ABC перейдет в ортоцентр треугольника ABC, составленного из средних линий исходного треугольника. Осталось заметить, что ортоцентр ABC совпадает с центром окружности, описанной около ABC. Кстати, коэффициент гомотетии одновременно указывает на отношение, в котором точка пересечения медиан делит отрезок, соединяющий ортоцентр с центром описанной окружности ABC.
8. Докажите сначала (используя свойства средних линий), что середины (точки A>1>, B>1>, C>1>) трех отрезков, соединяющих ортоцентр H треугольника ABC с его вершинами, лежат на окружности Эйлера. Если O>э> - центр окружности Эйлера, то относительно O>э> треугольники A>1>B>1>C>1> и ABC (A, B, и C - середины сторон ABC) будут ценрально-симметричными. Отсюда сделайте вывод, что точка O>э> является серединой отрезка, соединяющего точку H с центром описанной окружности около ABC.
В следующих книгах вы можете найти дополнительную информацию по данной теме.
Список литературы
1. В.В. Прасолов. Задачи по планиметрии. Ч. 2. Гл. 28. Инверсия. М., Наука, 1986.
2. Г.С.М. Кокстер. Введение в геометрию. Гл. 6. М., Наука, 1966.
3. И.М. Яглом. Геометрические преобразования. Т. 1,2. М., Гостехиздат, 1955-56.
4. И.М. Яглом. Окружности. Энциклопедия элементарной математики. Кн. IV. М., Гостехиздат, 1963.

Сноски:
1 Задача Фаньяно: в данный треугольник вписать треугольник наименьшего периметра.
2 Точкой Ферма остроугольного треугольника ABC называется точка M, для которой сумма MA+MB+MC принимает наименьшее значение.
3 Л. Маскерони(1750-1800), итальянский инженер, изучал математику самостоятельно. Работы относятся к теории геометрических построений, теории многоугольников, интегральному исчислению. Результаты его геометрических исследований доложил в 1797 году на заседании Национального института Наполеон Бонапарт.
4 Аполлоний(2-я половина 3 в.- 1-я половина 2 в. до н.э.). Родился в Перге (Малая Азия). Главный его труд "Конические сечения" сохранился не полностью (первые четыре книги) в оригинале, частично (три последующие книги) в арабском переводе, восьмая книга утеряна. Исследуя свойства конических сечений, их диаметров, фокусов, нормалей и касательных, пользовался проективно-геометрическими методами.
5 Круговым называется такое преобразованием множества {} ( - плоскость и - бесконечно удаленная точка), при котором каждая обобщенная окружность (т.е. окружность или прямая плоскости ) отображается на обобщенную окружность. Инверсия - частный случай кругового преобразования.
6 Л. Эйлер (1707-1783), математик, механик, физик и астроном. Родился в Базеле. С 1726 по 1741 и с 1766 являлся академиком Петербургской АН. Список трудов Эйлера содержит более 850 названий. Основные работы относятся к вариационному исчислению, интегрированию обыкновенных дифференциальных уравнений, степенным рядам, дифференциальной геометрии, теории чисел, небесной механике, оптике, гидродинамике. В конце 1766 года почти полностью потерял зрение, но, продолжая интенсивно работать, за 17 лет подготовил около 400 научных работ.
7 в случае, если треугольник ABC является тупоугольным.