Расчет стационарного теплового поля в двумерной пластине (работа 1)
Расчет стационарного теплового поля в двумерной пластине
Курсовая работа по сеточным методам
Студент: Смирнов А.В.
Московский Государственный Технический Университет им. Н.Э. Баумана
Москва 2002
Постановка задачи
Рассчитать установившееся температурное поле в плоской пластине, имеющей форму криволинейного треугольника с тремя отверстиями (см. рисунок).
К внешним границам пластины
подводится тепловой поток плотностью
.
На внутренних границах конструкции
происходит теплообмен со средой,
характеризующийся коэффициентом
теплообмена
и температурой среды
.
Коэффициент теплопроводности
материала пластины
Рис. 1Решение
Введем декартову систему
координат
,
выбрав начало координат и направим оси
x и y так,
как показано на рис.2.
Рис. 2
Задача теплопроводности в пластине запишется в виде
(1)
(2)
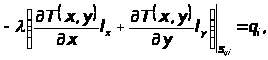
(3)
где
- направляющие косинусы вектора внешней
нормали к граничной поверхности,
- граничная поверхность, на которой
происходит теплообмен с коэффициентом
теплообмена
,
- граничная поверхность, на которой
задан тепловой поток плотности
.
Решение уравнения (1) с граничными условиями (2) и (3) можно заменить задачей поиска минимума функционала
.
(4)
Решать поставленную задачу будем с помощью метода конечных элементов. Для этого сначала проведем триангуляцию нашей области.
Триангуляция.
Результат триангуляции представлен на рис.3.
Рис. 3
Все выбранные узлы заносятся в список, который содержит информацию о координатах узлов. Номер узла определяется его номером в списке. Кроме списка вершин будем вести еще список треугольников. В глобальном списке треугольников будет храниться информация о каждом построенном треугольнике: номера (Top1, Top2, Top3) трех узлов, составляющих данный элемент и номер границы. Номер треугольника определяется его номером в списке. Договоримся, что у каждого треугольника границе может принадлежать только одна сторона и если такая сторона есть, то вершины, которые она соединяет, будут стоять на первых двух позициях (Top1 и Top2). Обход треугольника совершается против часовой стрелки.
Метод конечных элементов
Выберем произвольный
треугольник (с номером e).
Обозначим его вершины
и
.
Каждому узлу треугольника поставим в
соответствие функцию формы
,
(5)
где
,
A – площадь треугольника.
Тогда температуру в пределах треугольника
можно определить с помощью функций форм
и значений температуры
в узловых точках
.
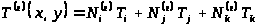(6)
Функционал (4) можно представить
в виде суммы функционалов
,
каждый из которых отражает вклад в
функционал (4) элемента с номером e
.
(7)
Минимум функционала (4) находим из условия
(8)
Функционал
можно представить в виде
(9)
Здесь
,
глобальный вектор температур
,
- матрица градиентов, которая для функций
формы (5) примет вид
,
.
Локальный вектор температур
.
Здесь матрица геометрических связей
имеет размерность
.
Элементы этой матрицы определяются
следующим образом:
;
все остальные элементы равны нулю.
Продифференцируем функционал (9):
Из выражения (8) с учетом
последнего соотношения получаем
,
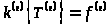где матрица теплопроводности элемента
;
вектор нагрузки элемента
.
В силу особенностей проведенной триангуляции можно выделить три группы конечных элементов. В первую входят треугольники, у которых сторона i – j принадлежит одной из внешних границ. Во вторую – те, у которых та же сторона принадлежит одной из внутренних границ. И, наконец, третью группу составляют элементы, стороны которых лежат внутри рассматриваемой области.
В зависимости от того, к какой
группе принадлежит конечный элемент с
номером e, матрица
и вектор
будут определяться несколько различным
образом.
Обозначим
.
Поверхностные интегралы
можно посчитать с помощью относительных
координат
.
Отрезки, соединяющие любую фиксированную
точку P треугольника e
c его вершинами, разбивают
этот элемент на три треугольные части
площадью
.
Координаты
определяются из соотношений
.
Используя относительные координаты, можно получить следующие соотношения:
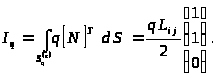
Если конечный элемент с
номером e принадлежит к
первой группе, то
.
Если ко второй, то
.
Наконец, если элемент принадлежит к
третьей группе, то
.
Вектор температур, удовлетворяющий условию (8) минимума функционала (4), находим решением системы линейных алгебраических уравнений
,
(10)
где глобальная матрица теплопроводности K и глобальный вектор нагрузки F определяются по формулам
,
.
(11)
Для решения задачи (10) применялся следующий алгоритм:
Вычисление
разложения матрицы
(
).
Оценка числа обусловленности.
Если число обусловленности больше
(
определяется точностью вычислительной
машины), то выдается предупреждение,
так как малые отклонения в коэффициентах
матрицы
могут привести к большим отклонениям
в решении.
.
.
Реализация описанного выше метода проводилась на языке программирования С++ и FORTRAN в среде интегрированной среде разработки Microsoft Visual C++ 6.0. Конечные результаты данной работы приведены на рис.4 - 7.
Рис.4
Рис.5
Рис.6
Рис.7
Список литературы
Амосов А.А, Дубинский Ю.А, Копченова Н.В. Вычислительные методы для инженеров: Учеб. пособие. – М.: Высш. шк., 1994. – 544 с.
Сегерлинд Л. Применение метода конечных элементов. – М.: Мир, 1979. – 392 с.
Станкевич И. В. Сеточные методы (лекции и семинары 2002 года).