Метод расчета скейлинговых констант Фейгенбаума для одномерных дискретных отображений по точкам сверхустойчивых циклов

Антон Никифоров

Напомню для начала некоторые факты из теории универсальности Митчелла Фейгенбаума. Будем называть непрерывное отображение отрезка в себя унимодальным, если внутри отрезка имеется точка экстремума и по обе стороны от неё отображение является строго монотонным (с одной из сторон возрастающим, с другой убывающим). Условимся далее рассматривать только унимодальные отображения вида

(1)

Если последовательность {} при данном r состоит из n точек, такую последовательность будем называть n-циклом, что =f( ), =f( ), …, =f( ) или . Заметим, что производная порядка n функции (n раз вычисленной функции f(x)) в точке x по правилу дифференцирования сложной функции равна .

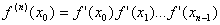Точки цикла, удовлетворяющие соотношению

(2)

называются неподвижными.

Величина (так называемый мультипликатор) определяет устойчивость n-цикла и её принято называть устойчивостью (stability, [2], p.121). n-цикл называется устойчивым, если <1.

n-цикл, содержащий в качестве одной из своих точек, называются сверхустойчивым. Для такого цикла =0.

Как было продемонстрировано в 1978 году М.Фейгенбаумом [4], значения параметра , при которых число устойчивых периодических точек удваивается и становится равным , удовлетворяют масштабному соотношению, или как говорят имеют скейлинг:

(3)

Данное соотношение встречается также и в следующей записи:

,n>>1 ([1], стр. 49),

(3.1)

Рис.1

Или в таком виде:

,(см. [2], p.3),

Расстояния от точки , где - точка экстремума рассматриваемого отображения (на рис 1. x=1/2), до ближайшей к ней точки на - цикле подчиняются следующему соотношению:

, n>>1

(4)

Константы Фейгенбаума имеют значения , и являются ни много ни мало мировыми транцедентными числами, такими как или e.

Сказку о том, как Фейгенбаум сидел в тени деревьев и вычислял их на своём калькуляторе HP-65 с золотистыми кнопочками вы, наверное, слышали. Это был первый программируемый калькулятор и стоил ни много ни мало аж 400 (четыреста!) долларов. Наивно полагать, что своё удивительное открытие Фейгенбаум сделал, пользуясь исключительно калькулятором: все-таки в то время он работал в Лос-Аламосе, а у военных всегда были и будут самые мощные компьютеры в мире, однако открытие действительно было чудесным - какие бы унимодальные отображения мы не рассматривали, скейлинг для них (т.е. "волшебные" числа и ) будет тем же самым.

Алгоритм

Интересно, что точки также можно использовать для расчета , этим факт мы и будем использовать в дальнейшем. Обратим внимание, что в точках мультипликатор всегда равен нулю, что автоматически означает устойчивость этих циклов:

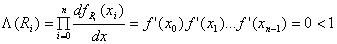
(a)	Например, для цикла периода два:
	, где
	, таким образом
		(5.1)

(б)	Цикл периода четыре:
	, где
	, таким образом
		(5.2)

Для произвольных же -циклов справедливо выражение:

(6)

Уравнение (5.3) легко решается относительно параметра , например, с помощью метода последовательных итераций Ньютона:

(6.1)

Здесь i - номер итерации. Таким образом, весь процесс вычисления, скажем, константы сводится к нахождению таких значений параметра R, при которых бифуркационная диаграмма пересекает линию . Для этого необходимо решить уравнение (6), проитерировав его раз.

НА ВХОД ПОДАЕМ:

Начинаем итерировать функцию f cо следующего значения:

Итерируем производную функции начиная с

Начальные приближения двух значений параметра R: ,

Разумное начальное приближение для постоянной :

НА ВЫХОДЕ ПОЛУЧАЕМ:

А весь процесс может быть описан следующими выражениями:

, n=2,3,4,…

, i=0,1,2,…

Рассмотрим на примерах как выглядят непосредственные вычислительные формулы.

ПРИМЕР 1:

При данном значении функция f будет зависеть только от константы r, обозначим эту функцию как . Тогда предыдущее уравнение можно будет переписать:

ПРИМЕР 2:

ПРИМЕР 3:

Программу расчета константы вы можете найти здесь. Её легко модицифировать для расчета постоянной , что предоставляется проделать читателю. Результат расчета в зависимости от шага i приводится ниже.

i
1	6.9032539091...
2	4.7443094689...
3	4.6744478277...
4	4.6707911502...
5	4.6694616483...
6	4.6692658098...
...	...
11	4.66920173800930...

Список литературы

[1] Г.Шустер, "Детерминированный хаос. Введение", М:Мир, 1988

[2] K.Briggs "Feigenbaum Scaling in Discrete Dynamical Systems", PhD thesis, 1997

[3] Е.Б.Вул, Я.Г.Синай, К.М.Ханин, "Универсальность Фейгенбаума и термодинамический формализм", УМН, т.39, вып.3(237), 1984

[4] М.Фейгенбаум, "Универсальность в поведении нелинейных систем", УФН, т.141, вып.2, октябрь 1983

[5] Н.Н.Калиткин, "Численные методы", М:Наука, 1978

[6] Метод Ньютона