Задачи выбора торговых посредников

ОБРАЗОВАТЕЛЬНАЯ АВТОНОМНАЯ НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ

«ВОЛЖСКИЙ УНИВЕРСИТЕТ имени В.Н. ТАТИЩЕВА» (ИНСТИТУТ)

Факультет – экономический

Специальность – маркетинг

Кафедра маркетинга и ИТ в экономике

КУРСОВАЯ РАБОТА ПО ДИСЦИПЛИНЕ

«Разработка маркетинговых решений»

на тему:

«ЗАДАЧИ ВЫБОРА ТОРГОВЫХ ПОСРЕДНИКОВ»

Тольятти 2009

Содержание

ВВЕДЕНИЕ

1. ЗАДАЧИ ВЫБОРА ТОРГОВЫХ ПОСРЕДНИКОВ

2. ПОСТАНОВКА И ОПИСАНИЕ ЗАДАЧ ПРИНЯТИЯ РЕШЕНИЙ

2.1. Технология принятия управленческих решений

2.2. Характеристика проблемной ситуации

2.3. Методы выбора предпочтительного объекта

3. ПРАКТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧ ПРИНЯТИЯ РЕШЕНИЙ

ЗАКЛЮЧЕНИЕ

СПИСОК ЛИТЕРАТУРЫ

Введение

В условиях перехода промышленных предприятий, объединений и других социально-экономических объектов (СЭО) к полномасштабным рыночным отношениям, подразумевающим настоящую организационно-хозяйственную самостоятельность, резко увеличивается круг вопросов, входящих в сферу деятельности аппарата управления, и в частности управления маркетинговой деятельностью.

Начатая экономическая реформа всего народного хозяйства, увеличение финансовой и хозяйственной самостоятельности СЭО, увеличение отдачи, эффективности от мероприятий по оптимальному управлению требуют перестройки организационных структур управления, совершенствования форм и методов процессов управления, повышения качества принимаемых решений. Принятые управляющие решения должны быть оптимальными и обоснованными не только на организационном уровне управления, но и в технической, кадровой политике, маркетинге и других сферах взаимодействия СЭО с внешней средой. Однако с увеличением круга решаемых задач (расширением проблемной области) резко возрастает информационный поток по сопровождению задач управления. Каждая такая задача требует адекватной совокупности информационных единиц, потенциально необходимой и достаточной для формирования информационного образа (ИО) ситуации (задачи) и соответственно способов ее разрешения. Система таких ИО ситуаций и образует проблемную область (ПО) лица, принимающего решения (ЛПР). Оперативное построение ПО ЛПР и генерация альтернатив часто затруднено как из-за отсутствия качественной информации для ИО, так и из-за неадекватности процедур формирования ИО и вариантов решения и непрерывного увеличения числа факторов, учитываемых при принятии решений, особенно в маркетинговой деятельности.

1. Задачи выбора торговых посредников

Когда дело доходит до сбыта, вам необходимо решить основной вопрос (решение которого, однако, влечет за собой череду других вопросов) - продавать товар самостоятельно или через посредников. Это решение зависит от множества факторов:

- целей сбыта;
- его планируемой интенсивности;
- ресурсов вашей компании;
- особенностей потребителей и их требований к местам продаж;
- особенностей товара и доступности каналов товародвижения (посредников).

Далее, если вы решили продавать свой товар через посредников, вам необходимо:

- определить длину канала и принципы взаимодействия с посредниками;
- выбрать торговые точки, удовлетворяющие определенным, необходимым для продажи вашего товара, условиям.

Таким образом, чтобы выстроить успешную систему сбыта ваших товаров либо услуг, вам необходимо ответить на следующие вопросы (именно в указанной последовательности):

- Каковы цели сбыта?
- Какой должна быть интенсивность сбыта (через какое количество торговых точек планируется продавать товар)?
- Следует ли сбывать товар самостоятельно либо стоит прибегнуть к помощи посредников?
- Через какие типы торговых организаций нужно продавать ваш товар?
- Как должно строиться взаимодействие с посредниками?

Возможно, у некоторых владельцев малых и средних предприятий перечисление всех этих этапов вызовет усмешку - ведь многим приходится отдавать свою продукцию туда, где ее согласны взять, а уж построение собственных каналов сбыта представляется на этом фоне непозволительной роскошью. Однако если вы будете знать, как может быть организована система распределения, вы, вероятно, сможете найти отдельные моменты, которые можно будет применить и в вашем случае.

Прежде, чем перейти непосредственно к рассмотрению этапов создания системы сбыта, заметим, что при выборе каналов распределения вы должны постоянно учитывать пять факторов:

- ваши потребители: их характеристики и потребности;
- ваше предприятие: его цели, ресурсы, знания и опыт руководства и персонала;
- ваш товар или услуга: стоимость, сложность, сохранность, размеры;
- ваши конкуренты: характеристика и особенности поведения;
- имеющиеся каналы товародвижения: альтернативы, характеристики, доступность.

Так как цели сбыта являются неотъемлемой частью системы целей предприятия, то они должны быть согласованы с общими целями и целями других подразделений.

Например:

Ситуация 1. Предприятие, занимающееся производством женской одежды, планирует увеличить объемы производства. В таком случае целями распределения будут увеличение его интенсивности - т.е. увеличение числа торговых точек, через которые будет распространяться его продукция.

Ситуация 2. Предприятие, выпускавшее ранее дешевые шампуни и продававшее их на мелкооптовых рынках, столкнувшись с резким снижением спроса на свою продукцию, стало выпускать шампуни более высокого качества в средней ценовой категории. В данном случае целями сбыта будет пересмотр принципов распределения, т.е. переход от рынков к более цивилизованным формам торговли.

Интенсивность распределения определяет, сколько торговых предприятий будет участвовать в реализации вашей продукции, и зависит от того, насколько доступен должен быть ваш товар для потребителя. Различают три вида интенсивности распределения:

- интенсивное,
- селективное (избирательное),
- эксклюзивное.

Интенсивное распределение означает стремление максимизировать возможное количество точек распределения товара. Иными словами, предприятие, использующее интенсивное распределение, стремится сделать свой товар максимально доступным для потребителей. Такую стратегию выбирают предприятия с массовым и крупносерийным производством, выпускающие товары, покупаемые с минимальными усилиями. Так, такой способ распределения характерен для большинства продуктов питания (например, хлеб, молоко, шоколад, мороженое, минеральная вода и т.п.) среднего и низкого ценового сегментов. Основные достоинства данного метода - предоставление практически всем потенциальным потребителям возможности купить данный товар и рост узнаваемости вашей марки. Однако при использовании этой модели распределения невозможно контролировать цены и качество обслуживания во всех торговых точках, что может отрицательно сказаться на имидже производителя. Интенсивное распределение не подходит для товаров длительного использования (например, бытовой техники), во-первых, по уже указанной причине невозможности контроля за всеми торговыми точками, а во-вторых, реальной опасности затоваривания рынка. Кроме того, для продажи высокотехнологичных товаров, к которым относится, в том числе, бытовая техника, компьютеры, требуется квалифицированный персонал, наличие которого сложно гарантировать при большом числе мест продажи.

Селективное (избирательное) распределение заключается в том, чтобы выбрать определенные торговые точки, которые лучшим образом подходят для реализации именно вашего товара, или для обслуживания ваших целевых покупателей. Селективное распределение используется для продажи товаров предварительного выбора, например, мебели, бытовой техники, одежды, дорогих, технически сложных и нуждающихся в послепродажном обслуживании товаров.

Эксклюзивное распределение заключается в намеренном ограничении числа потребителей товара и числа предприятий, реализующих его. Как правило, такое распределение применяется для уникальных (вследствие их дороговизны либо присущих им качеств) товаров (дорогая парфюмерия и одежда, ювелирные изделия и т.п.), либо товаров, для приобретения которых покупатели согласны затратить значительные усилия. В этом случае важно отобрать в качестве торговых посредников организации, которые способны обеспечивать необходимое качество обслуживания и уровень цен на товар, имидж которых будет сочетаться с имиджем продаваемых товаров.

Таким образом, интенсивность распределения вашего товара зависит от ваших ответов на три основных вопроса:

- Сколько времени, денег и сил готов затратить потребитель ради покупки именно этого товара. Если много (например, готов ехать через полгорода ради покупки одежды определенной марки) - следует выбрать селективное или эксклюзивное распределение, если мало (например, продукты питания, которые покупаются возле дома) - интенсивное.

- Какой объем продаж вашего товара вас устроит? В случае если вы стремитесь к максимизации объемов продаж вашего товара, следует выбирать интенсивное распределение, в противном случае - селективное либо эксклюзивное.

- Какова емкость рынка вашего товара? Если небольшая - следует подумать об эксклюзивном распределении товара, большая - об интенсивном.

Длина канала распределения определяется количеством включенных в него звеньев. Звенья канала распределения - это производитель, потребитель и торговые организации, осуществляющие доставку товаров первого ко второму. Выделяют два основных типа каналов распределения: прямой и косвенный.

Прямой канал - продажа товаров производителя напрямую от производителя к потребителю, минуя посредников.

Косвенный канал - канал распределения товаров от производителя к потребителю с участием посредников.

Прежде, чем сделать выбор: заниматься сбытом самостоятельно или привлекать к этому посредников, следует знать, какие функции, кроме, собственно, сбыта, выполняет посредник.

Итак, функции посредников:

- Функция формирования ассортимента. Производители выпускают ограниченный ассортимент продукции, тогда как покупатели предпочитают иметь широкий выбор.

- Функция сортировки и фасовки. Производителям удобнее выпускать большие партии однотипной продукции, а покупатели приобретают товары в ограниченном количестве.

- Функция хранения. Потребители покупают товары не сразу после того, как они были произведены, а спустя достаточно длительное время. Все это время товар, как правило, хранится у посредника.

- Функция транспортировки. Производители чаще всего производят свой товар совсем не там, где находятся их потребители (по крайней мере, их часть), соответственно, товар нуждается в транспортировке до места продажи.

- Функция финансирования. Посредник участвует в создании дополнительной стоимости товара, создавая комфортные условия его приобретения.

- Информационная функция. Так как посредник общается непосредственно с потребителем, на него ложится обязанность отслеживать его поведение, реакцию на товары, ее изменение и прочие особенности.

Таким образом, если производитель решает взять на себя обязанности посредника, то ему придется выполнять ВСЕ эти функции.

Чтобы облегчить вам принятие окончательного решения, приведем плюсы и минусы каждого варианта организации сбыта.

Таблица 1. - Достоинства и недостатки различных каналов сбыта

Виды	Достоинства	Недостатки
ПРЯМОЙ КАНАЛ СБЫТА
 заказы по почте;  продажи по телефону;  продажи по каталогу;  личные продажи;  собственная розничная сеть.	 простая структура распределения, обеспечивающая контроль над каналами сбыта;  отсутствие необходимости делиться прибылью;  возможность непосредственного общения с потребителями и получения сведений об их реакции на товар <из первых рук>	 сложность организации (включая организационную, финансовую и управленческую стороны вопроса).
КОСВЕННЫЙ КАНАЛ СБЫТА
 короткий канал, если имеется только одно звено между производителем и потребителем - розничный продавец;  длинный канал, если наряду с розничным торговцем в цепочке появляется оптовик.	 обеспечение широты охвата аудитории (это сложно сделать с помощью прямого канала);  увеличение скорости оборота и валового дохода;  специализация: каждый участник канала товародвижения выполняет свою функцию.	 отсутствие контроля за каналом распределения, слабая возможность контролировать цены и условия продаж, зависимость от посредников;  отсутствие возможности прямого общения с покупателями.

Окончательный выбор длины канала сбыта зависит от особенностей клиентов, товара, предприятия, конкуренции и канала сбыта.

Особенности клиентов

Прямой канал сбыта: компактный целевой рынок, товар приобретается редко, но в больших количествах, небольшое количество крупных потенциальных клиентов, работа на рынке (межфирменной торговли).

Косвенный канал сбыта: обширный целевой рынок, товар приобретается часто, но в небольших количествах, большое количество потенциальных клиентов, работа на потребительском рынке.

Особенности товара

Прямой канал сбыта: дорогие товары, громоздкие товары, товары, требующие специального обслуживания, изготовленные по заказу клиента, товары с коротким сроком хранения.

Косвенный канал сбыта: стандартные товары повседневного спроса с достаточно большим сроком хранения.

Особенности предприятия

Прямой канал сбыта: наличие свободного капитала, информации о рынке, наличие квалифицированных продавцов и умение руководителей справиться с управлением собственными магазинами.

Косвенный канал сбыта: отсутствие всего вышеперечисленного или его значительной части.

Особенности конкуренции

Прямой канал сбыта: все привлекательные посредники работают с конкурентами на эксклюзивной основе.

Косвенные каналы сбыта: сравнительно низкая представленность конкурентов среди привлекательных посредников.

Особенности каналов сбыта

Прямой канал: среди существующих посредников нет удовлетворяющих вашим требованиям либо они недоступны (предлагают невыгодные условия сотрудничества либо вообще отказываются от него).

Косвенный канал: среди существующих посредников есть соответствующие требованиям предприятия, условия сотрудничества приемлемые.

Как выбрать посредника

Итак, вами уже принято решение: продавать товар самим либо через посредника. Если вы решили, что справитесь со сбытом вашего товара самостоятельно, то вам остается найти место для вашего магазина (магазинов), закупить оборудование, нанять персонал, сообщить об открытии торговой точки покупателям и ждать получения первых доходов от продажи ваших товаров.

Если вы, взвесив все <за> и <против>, решили реализовывать свой товар через посредника, то перед вами встал вопрос выбора этого самого посредника (или посредников - оптовых и розничных).

Факторы, которые необходимо учитывать при выборе посредника:

- имеет ли посредник выход на ваш целевой рынок;

- сможет ли он удовлетворить потребности клиентов, предоставляя им ваши товары и услуги;

- сможет ли он обеспечить достаточный оборот товаров, чтобы они не лежали на складе;

- имеет ли он возможности для хранения товаров;

- достаточно ли он настойчив в продвижении ваших товаров и услуг;

- сможет ли он работать в условиях конкуренции;

- будет ли он работать с вами;

- каково его финансовое положение;

- каковы его управленческие способности.

После выбора посредников, подходящих вам, необходимо убедить их, что вы им тоже подходите. Для этого целесообразно подготовить и представить посреднику следующую информацию:

- преимущества ваших товаров перед товарами конкурентов;

- потребности клиентов, которые будут удовлетворены с помощью ваших товаров;

- результаты исследования рынка, проведенного вами;

- предполагаемый объем реализации ваших товаров;

- способы стимулирования сбыта ваших товаров;

- какую выгоду сможет получить посредник от сотрудничества именно с вами.

Следует отметить, что существуют два основных способа заинтересовать посредников работой с вашим предприятием.

Протягивающее распределение. При использовании данного метода производитель напрямую стимулирует спрос потребителя на продукт. Таким образом, конечный потребитель, заинтересовавшись товаром, начинает спрашивать его у посредника, а у того не остается иного выхода, кроме как включить этот товар в свой ассортимент.

Проталкивающее распределение. При проталкивающем распределении производитель стремится заинтересовать товаром не потребителей, а посредников, путем:

- привлечения внимания к прибыльности продукта через рекламу и представителей, информирующих торговлю;

- увеличения прибыльности продукта для торговли за счет торговых наценок, особых условий сделок, премии за высокий объем продаж и временных стимулирующих мероприятий.

Резюме

Итак, для того, чтобы выстроить систему сбыта ваших товаров в соответствии со всеми правилами, необходимо:

- Установить цели сбыта, связав их с целями всего вашего предприятия и отдельных его подразделений;

- Определить интенсивность распределения вашего товара, ориентируясь на заинтересованность потребителей в его покупке, желаемый объем продаж и емкость рынка;

- Определить длину канала распределения, сопоставив все достоинства и недостатки прямого и косвенного каналов сбыта, а также взвесив свои силы и возможности по организации канала сбыта и выполнению всех посреднических функций;
- Выбрать посредника (или посредников), способного успешно продавать ваш товар и согласного работать с вами;
- Заинтересовать посредника (посредников) работой с вами и вашим товаром с помощью воздействия непосредственно на него, либо на конечных потребителей вашего товара.

2. постановка и описание задач принятия решений

Информация по формированию и оценке решений упорядочивается в виде соответствующих матриц (таблиц). При этом для каждого типа задач принятия решений формулируется своя система подготовки и представления информации . В свою очередь , каждая задача по принятию маркетинговых решений характеризуется некоторыми классификационными параметрами.

При подготовке информации для описания и анализа проблемной ситуации обычно используют некоторые типовые модели, полнота описания которых зависит от типа решаемой задачи.

Обычно в качестве основных параметров, определяющих тип задачи и соответственно структуру ее описания , выбирают следующие:

- количество лиц, принимающих решение (один ЛПР – характеризуют задачи индивидуального выбора, а признак принимает значение - J; несколько ЛПР – характеризуют задачи группового выбора типа, а признак принимает значение - G) ;

- наличие/отсутствие полной информации о проблемной ситуации и направлениях ее развития (в случае полной информации признак принимает значение -  (пусто); если информация неполная или нечеткая, то формулируются гипотетические ситуации, моделирующие возможные варианты развития проблемы, а признак принимает значение – S);

- наличие одного или нескольких критериев выбора (если критериев несколько, то данный признак принимает значение –А; если критерий один, то признак принимает значение -  (пусто).

Тогда с учетом возможных проявлений признаков классификации, можно сформулировать следующую обобщенную структуру группировки задач.

Задачи индивидуального выбора: тип J (с полной информацией, индивидуальный выбор по одному критерию); тип JA (с полной информацией, индивидуальный выбор по нескольким критериям); тип JS (с неполной информацией, индивидуальный выбор по одному критерию); тип JSA (с неполной информацией, индивидуальный выбор по нескольким критериям).

Задачи группового выбора: тип G (с полной информацией, групповой выбор по одному критерию); тип GA (с полной информацией, групповой выбор по нескольким критериям) тип JS (с неполной информацией, групповой выбор по одному критерию); тип GSA (с неполной информацией, групповой выбор по нескольким критериям).

Определим систему описания информации для некоторых классов задач .

Задачи типа J. Они характеризуются полной информацией по проблеме и альтернативам решения, наличием одного критерия и одним ЛПР, который и осуществляет выбор. Информация описывающая эти задачи ,как правило, представлена, в виде простой таблицы (табл.1).

Таблица 1.

Матрица описания задач типа J

Альтернативы решения	Y_>1>	Y_>2>	…	Y_>n>
Функции предпочтения	f_>1>	f_>2>	…	f_>n>

Для вычисления значений функции предпочтения (f_>i>) по каждой альтернативе может быть использована любая шкала: - ранговая (порядковая); - количественная (степени достижения); - относительная и др. В дополнение к матрице может быть дана информация об особенностях решения, условиях, ограничениях и возможностях.

Задачи типа JS. Для них характерна неопределенность в описании проблемы и/или альтернатив решения, т.е. проблемная ситуация S_>o> полностью не определена . В этом случае ситуация So доопределяется гипотетическими ситуациями S_>i> , т.е. S_>o> = ( S_>1>, S_>2>,…, S_>n> ) и для каждой из ситуаций, если это возможно, следует задать вероятность ее возникновения.

Задачи данного типа характеризуются одним критерием выбора и множеством гипотез ( S_>1>, S_>2>,…, S_>n>) с вероятностями их возникновения Р(S_>i>).

Информация описания задачи такого типа чаще всего представляется матрицей, где f_>ij> – функция предпочтения ; Р_>i> - вероятность появления ситуации S_>i> (таб. 2)

Задачи типа JA. Данный тип задач характеризуется наличием нескольких целей (критериев) (многокритериальные задачи) А = (А_>1>,А_>2>,…,А_>k>) и характеризуют вполне определенную проблемную ситуацию.

Для каждой цели (критерия ) могут быть определены приоритеты b_>i>, задающие степень ее важности. Информация описания такой задачи представляется следующей матрицей (табл. 3) .

Задачи типа JSA. Данный класс задач относится к многокритериальным и характеризуются наличием системы гипотез развития проблемы S_>o> = ( S_>1>, S_>2>,…, S_>n> ), для каждой из которых задается вероятность ее возникновения. Множество целей А = (А_>1>,А_>2>,…,А_>k>) задает критериальное пространство решения, для каждой из которых формируется приоритет цели b_>i>. Описание такой задачи характеризуется матрицей, представленной в табл. 4 .

К задачам группового выбора относятся задачи типа G , GS , GA , GSA

Методология решения задач группового выбора

В практике управления часто встречаются такие проблемные ситуации, для которых частично или полностью неизвестна или труднодоступна информация для описания проблемной ситуации или которые невозможно формализовать с достаточной точностью. В этом случае такие проблемы обычно решаются с помощью привлекаемой группы экспертов, анализирующих и оценивающих имеющуюся проблемную ситуацию и генерирующих некоторое множество альтернатив ее решения. Сама процедура проведения экспертного опроса и оценки мнений проводится в несколько этапов:

- отбор и формирование экспертной группы. Формирование группы обычно сводится к отбору группы экспертов. При этом необходимо учитывать следующие факторы, которым должен отвечать эксперт и соответствие которым необходимо отслеживать: - компетентность, - независимость, - его деловые качества, - совпадение целей экспертизы для экспертов. Количество экспертов в группе должно составлять от 5 до 15 человек (оптимальный вариант).

- проведение опроса. В этом случае необходимо задать процедуру оценивания, указать тип шкалы, по которой необходимо оценивать объекты, и определить основные оцениваемые параметры объектов. Процедура оценивания обычно проводится в виде интервью , анкетирования , дискуссии.

- обработка данных. Данные сводятся в специальные таблицы как отдельно по каждому эксперту, так и по всей группе в целом. Обработка может быть количественной (статистической) и качественной. При этом оцениваются как эксперты, так и сама ситуация. На основе личных оценок каждого эксперта вычисляются групповые приоритеты, которые дополнительно оцениваются на достоверность, причем могут считаются таковыми, если индивидуальные оценки экспертов согласованы между собой (не разбросаны). В качестве критерия достоверности могут быть использованы коэффициенты согласия, вычисляемые на базе коэффициента множественной корреляции.

-производится формирование решений с использованием различных известных стратегий принятия решений .

Задачи типа G. Эти задачи характеризуются наличием вполне определенной ситуации, одним критерием выбора и несколькими экспертами, осуществляющие выбор по заранее определенным правилам, G = (J_>1>, J_>2>,…, J_>m>). Информация , описывающая такие задачи, обычно представлена простыми матрицами, но таких матриц будет столько, сколько членов в экспертной группе (m – число членов экспертной группы, каждый из которых решает однокритериальную задачу с n – альтернативами (табл. 5 ).

Таблица 5 .

Матрица описания задач типа JSA ЛПР_>1>…… ЛПР_>m>

Альтернативы	Y_>1>	Y_>2>	…	Y_>n>	…	Альтернативы	Y_>1>	Y_>2>	…	Y_>n>
Функции	f_>1>	f_>2>	…	f_>n>	…	Функции	f_>1>	f_>2>	…	f_>n>

Каждый ЛПР- член экспертной группы, на основании решения задачи формирует наилучшее решение Y_>j>^*. Далее строится матрица эффективных решений (табл.6), из которых следует выбрать наилучшее решение.

Таблица 6

Матрица эффективных решений ЛПР

ЛПР	J_>1>	J_>2>	…	J_>m>
Функции	f_>1>^*	f_>2>^*	…	f_>m>^*

Для выбора наилучшего решения Y^* по f^*, из множества (f_>1>^*, f_>2>^*,…, f_>m>^*), необходимо сформулировать правила (механизм) согласования мнений экспертов.

Задачи типа GS , GA , GSA . Данные задачи аналогичны задачам типа JS , JA , JSA и информация описания таких задач представляется матрицами (табл. 2 , 3, 4). Количество матриц соответствует числу экспертов в группе.

2.1 Технология принятия управленческих решений

Технологические процессы и операции по принятию управленческих решений осуществляются лицом, принимающим решение, в 4 обобщенных этапа:

формирование и оценка решений;
подготовка к выбору решения;
технология процедур принятия решений;
моделирование процедур принятия решений.

1. Механизм формирования решений – это творческий процесс, требующий анализа и синтеза всех предшествующих элементов времени и ресурсов, ограничений, целей и др.

При формировании решений обычно используют следующий алгоритм действий (последовательность этапов формирования решений);

Определить возможную область и характер решений.
Определить тип решений.
Сформулировать крайние варианты множества решений (идеальный и наихудший).
Сформировать альтернативы, расположенные между ними.
Провести качественное описание ожидаемых преимуществ и недостатков альтернативных вариантов решений.
Оценить вероятность реализации решений.
Произвести сравнительную оценку предпочений по достижению цели.

На первом этапе предварительный анализ ПС дает возможность определить область решения: экономического, технического, организационного, технологического и д.р., которые сужаются до определенных сфер управленческой деятельности.

На втором этапе определяется тип возможных решений. Условно можно выделить 3 этапа решений:

- стандартные решения, применяемые для типовых проблемных ситуаций;

- решения - усовершенствования;

- оригинальные.

Опыт управленческой деятельности показывает, что наибольшее распространение по количеству формируемых решений при управлении получили решения типа решения – усовершенствования. Это объясняются тем, что большинство экономических ситуаций, требующих принятия управленческих решений, имеют аналоги (прототипы), для которых известны решения, и для новых аналогичных ПС формируют идентичные решения с некоторыми различиями и особенностями.

Естественно при этом необходимо иметь ввиду, чтобы количество различий не переросло в качественно новую ситуацию. Так как в этом случае необходимо видоизменять класс проблемных ситуаций или формировать новый.

Оригинальные решения используются в том случае, когда известные решения-прототипы не подходят и нужен новый подход к разрешению ПС. Здесь обычно используются методы генерации идей (решений), основанные на следующих подходах:

А) мозговой штурм;

Б) экспертный (системный подход) вывод;

В) генерация альтернативных решений.

При решении ПС данными методами обычно генерируют несколько альтернативных решений, удовлетворяющих заданным требованиям. Их вырабатывают столько, сколько можно получить по имеющимся входным данным и ограничениям. Из полученного множества отбираются наиболее эффективные решения, а из них – оптимальные (наилучшие).

На третьем этапе для обеспечения уверенности в степени полноты, генерируемого множества решений целесообразно сформулировать два крайних варианта альтернатив: максимально желательный и минимально нежелательный. Формирование этих крайних вариантов дает некоторую шкалу, на которой можно задать оценку и направление изменения промежуточных вариантов решения для достижения максимального или ухода от минимального.

Генерация промежуточных вариантов выполняется на четвертом этапе.

Для каждого сгенерированного варианта необходимо провести анализ на рациональность и достижимость возможных решений и дать качественное описание ожидаемых преимуществ и недостатков по каждому варианту. Эта задача решается на пятом этапе формирования решений.

В качестве критерий оценки альтернативных решений в этом случае можно использовать значения степени (вероятности) выполнимости решения, анализ которого проводиться на шестом этапе.

При формировании системы предпочтений при выборе решения вырабатываются критерии сравнения и оценки вариантов решения, которые необходимо описывать как на качественном уровне, так и, если возможно, на количественном (т.е. максимально использовать количественные оценки, технические характеристики; экономические показатели, например прибыль, затраты и др..). На основании полученных оценок строится таблица (матрица), характеризующая постановку задачи и по значению которой осуществляется выбор решения по обоснованному заранее методу принятия решения. Решение этой задачи осуществляется на седьмом этапе.

Краткое изложение действия при формировании решений и их оценки предполагают следующую последовательность операций: определение сферы и характера решения, выявление типа решения, разработка множества альтернативных решений, определение степени реализации альтернативных решений, выбор критериев и оценка предпочтений.

2. Подготовка к выбору решения.

После выполнения подготовительных работ по формированию и оценке решений формируется процедура непосредственного выбора решения.

На первом этапе упорядочивается полученная на предыдущих этапах информация и размещается в соответствующих матрицах (таблицах). При этом для каждого типа задач принятия решений формируется своя система подготовки и предоставления информации. В свою очередь, каждая задача ПР характеризуется классификационными параметрами.

При подготовки информации для описания и анализа проблемной ситуации используют некоторые типовые структуры, полнота описания которых зависит от типа решаемой задачи. Обычно в качестве основных параметров, определяют типы задач и соответственно структуру ее описания, выбирают следующие:

- количество лиц, принимающих решение (один ЛПР – характеризуют задачи индивидуального выбора, а признак принимает значение – типа J; несколько ЛПР – характеризуют задачи группового выбора типа, а признак принимает значение – типа G) ;

- наличие гипотез по дальнейшему развитию исходной ситуаций при отсутствии необходимой информации по проблеме, методологии решения или характеристик альтернативы (возможных вариантов развития событий) задает тип задачи S;

- наличие одного или нескольких критериев (если критериев несколько, то задача имеет тип А).

Определим систему описания информации для некоторых классов задач, наиболее часто встречающихся в практике управления.

Таблица 1.

Матрица описания задач типа J

Альтернативы решения	Y_>1>	Y_>2>	…	Y_>n>
Функции предпочтения	f_>1>	f_>2>	…	f_>n>

К задачам группового выбора относятся задачи типа G , GS , GA , GSA

3. Процесс управления с точки зрения выполнения шагов управления представляет собой систему действий, которую можно условно называть технологией (технологическим процессом) принятия решений.

Весь процесс подготовки и принятия решения можно представить в виде следующих этапов;

выявление проблемной ситуации, определение цели решения и критериев оценки его результатов;
информационный цикл, этап сбора информации для ознакомления с вопросом, по которому принимается решение (это самый важный этап, он требует наиболее квалифицированного труда, умения анализировать, выбирать наилучший вариант решения);
организация выполнения принятого решения (разработка плана реализации решения, определение сроков выполнения операций, назначение ответственных лиц, инструктаж и другие мероприятия, которые могут потребоваться для выполнения принятого решения);
контроль выполнения решения.

Только при сочетании всех звеньев процесса управления и соблюдении всего технологического цикла принятия решения этот процесс будет осуществлен с учетом объективной информации на научной основе. Подготовка, принятие и реализация решений как процесс управленческого труда имеют определенную технологию, определяемую в виде совокупности последовательно применяемых приемов и способов достижения целей деятельности.

Процесс решения с технологической точки зрения можно представить в виде последовательности этапов и процедур, имеющих между собой прямые и обратные связи. Предлагается следующая схема процесса подготовки, принятия и реализации решения.

1-й уровень – организационный;

2-й уровень – информационный;

3-й уровень – технологический.

Первый уровень позволяет выявить этапы, отличающиеся структурной организацией работы. По организационно-структурной схеме различают следующие этапы:

подготовка и анализ данных;
подготовка задачи;
разработка альтернатив;
принятие решения.

Второй уровень выделяет этапы, различающиеся по характеру используемой информации. По такой информационной схеме выделяются следующие этапы:

получение и подготовка данных;
формулировка проблемной ситуации;
подготовка задач;
разработка модели и метода решения;
разработка альтернатив;
прогноз и оценка;
определение (уточнение) критериев выбора;
выбор;
оформление решения.

Третий уровень показывает группы однородных технологических операций в процессе решения, т.е. операций по обработке информации,- информационную технологию. Здесь выделяют следующие этапы:

поиск, получение и восприятие данных;
фильтрация «сжатие» данных;
выявление ситуаций и постановка проблемы;
определение проблемной ситуации;
структуризация проблемной ситуации;
квантификация факторов и связей;
определение целей, критериев, условий;
согласование и оценка компонентов задачи;
формулировка задачи;
разработка моделей решения задач;
поиск, разработка и выбор процедуры решения задачи;
разработка альтернатив;
группировка альтернатив по целям, условиям и др.;
прогноз и оценка реализуемости альтернатив;
прогноз и оценка следствий реализации альтернатив;
определение частных критериев и предпочтений для выбора альтернатив;
обобщение критериев и предпочтений;
выбор решения;
интерпретация и оценка результатов выбора;
реализация решения.

Подготовка и анализ данных по проблемной ситуации. На информационном уровне анализируется исходная информация о состоянии объекта исследования – проблемы и внешней среды, воздействующей на проблему, определяются место и роль анализируемых объектов исследования среди смежных объектов и объектов более высокого иерархического порядка, осуществляется выявление, структуризация и ранжирование целей проблемной ситуации, проводится формализация проблемы.

При формулировании проблемы прежде всего определяются стратегические направления решения выявленной проблемы для последующего формирования целей. Стратегические варианты решения выявленной проблемы излагаются в сценарии развития проблемной ситуации.

Технологический уровень задает конкретное содержание каждого этапа данного организационного уровня.

Конечным результатом работ на первом этапе выработки решения является определение проблемной ситуации в виде выявления так называемых базовых, кардинальных проблем, за решение которых надо браться в первую очередь, ранжирование этих проблем, если их несколько, выбор стратегического направления их решения с предварительной ресурсной оценкой.

Подготовка задачи принятия решения. На этапе информационной подготовки задачи делается обобщение информации о проблеме и строится формальная постановка задачи. Для этого на технологическом уровне проводится четкая структуризация проблемной ситуации. При формировании целей определяются условия и ограничения на решение проблемы и согласовываются все компоненты проблемной ситуации. Цели должны иметь конкретные формулировки и количественные характеристики, по которым можно будет судить о степени их достижения. В конечном счёте приводится полная и емкая формулировка решаемой задачи.

Разработка альтернатив проводится в виде выделения полного перечня альтернатив. На этом этапе информационного уровня определяются потенциальные методы и модели решения проблемы, затем выявляется полная совокупность альтернативных вариантов достижения поставленных целей. Далее необходимо провести оценку развития и степени реализуемости каждой из возможных вариантов.

На технологическом уровне конкретизируются разработка и группировка альтернатив и методологии прогнозной оценки динамики изменения проблемы под воздействием той или иной альтернативы решения. Это и является конечным результатом работ на третьем этапе. В реальных условиях обычно рассматривают два-три варианта решения, не более.

Принятие решения сводится к выбору из допустимых альтернативных решений наилучшего. На информационном уровне определяются критерии эффективного выбора, проводится сама процедура выбора и оформляются процедура решения и методология реализации решения.

Технологический уровень охватывает конкретные действия по определения предпочтений выбора. Выбор лучшего решения проводится на базе детального анализа допустимых решений с точки зрения достижения поставленных целей, затрат ресурсов, соответствия конкретным условиям реализации решения.

2.2. Характеристика проблемной ситуации

Для проведения анализа и структуризации проблемной ситуации в экономической системе надо сформулировать необходимое и достаточное описание самой ПС. Если все параметры ПС определены и известны количественные значения ее характеристик, то формирование структуры описания не представляет трудностей. В каждом случае мы имеем дело с определенными задачами принятия решений. Сложнее, когда имеет место некоторая неопределенность в состоянии экономической системы и необходимо формулировать ПС в условиях неопределенности. Большинство реальных задач принятия решений относится именно к этому классу. С другой стороны, при использовании различного рода интегрированных систем поддержки процедур принятия решений необходимо определять структуру описания неопределенных ситуаций в системном представлении.

В этих целях обычно используется инструментарий искусственного интеллекта (экспертных информационных систем), аппарат нечетких множеств, метод продукций, методология семантического представления проблемной ситуации. Кратко рассмотрим некоторые основные положения приведенных представлений проблемы.

Структура представления ПС при их представлении в формализованном виде для систем поддержки решений состоит из двух уровней. На первом уровне используется система представления типовых ситуаций, на втором – универсальных ситуаций, по которым необходимо генерировать уникальные, оригинальные решения.

Формализация проблемы преимущественно в виде специфического семантического представления ПС объясняется еще и тем, что в систему поддержки принятия решения встраивается механизм экспертной поддержки для генерации и синтеза возможных альтернативных решений. Кроме возможности использования и автоматизированной системе представление проблемной ситуации в виде таких семантических описаний позволяет подробно структурировать проблему по целям и факторам развития.

Для представления и работы с такими представлениями ПС, необходимо сформулировать принципы реализации описания ситуации в виде таких семантических нечетких представлений.

Составной проблемой в задачах принятия решений являются исследование и формальное описание проблемных ситуаций, относящихся к неструктуризованным, т.е. имеющим неопределенное, нечеткое описание ситуации. Такие задачи обычно характеризуют наиболее важные глобальные изменения в структуре и стратегии функционирования экономических систем и решаются с помощью автоматизированных систем поддержки принятия решений.

Для вполне определенных проблемных ситуаций существуют методы формализованного представления в виде четких ориентированных графов, для которых используются стандартное графовое представление и операции с графами. Поэтому в литературе существуют определенные методики решения задач, представленных в виде орграфов. Наиболее сложными и труднореализуемым этапом при решении неструктурированных задач является их представление в системном виде (в компьютерном виде).

Нечеткой ситуацией экономической системы называют некоторое нечеткое множество признаков описания атрибутов состояния, определяемое как проблемная ситуация. Такое множество характеризуется набором признаков.

На этапе определения характеристик ПС развертывается описание таких характеристик, как точность, полнота, достоверность описания ПС. Так, например, характеристика полноты получается развертыванием описания проблемы по определенной атрибутивной системе, т.е. необходимо четко ответить на следующие вопросы: что, где, когда, почему, с какой целью, при каких условиях. В этом случае, если имеется четкая, вполне определенная ПС, используют обычно типовое описание, т.е. ряд типовых параметров для характеристики ситуаций, описанных ранее.

При недостаточной полноте описания ПС у ЛПР есть два варианта последующих действий: либо искать недостающую информацию, затрачивая при этом дополнительные время и ресурсы, либо принимать решение в условиях имеющейся неопределенности.

Формирование множества альтернативных ситуаций снижает неопределенность ПС, так как ясным становится полный перечень ситуаций, появление которых можно оценить в виде вероятностной величины. Степень разрешимости проблемной ситуации, определяется на ее начальной стадии, так как, возможно, ПС такова, что не имеет смысла заниматься ее решением, либо она неразрешима в данных условиях при данных ограничениях и данном ЛПР.

2.3 Методы выбора предподчительного объекта

Измерение характеристик при выборке наиболее предпочтительного объекта из некоторого множества альтернатив предполагает наличие в качестве объектов измерения некоторой совокупности характеристик, которые описывают сам экономический объект или проблемную ситуацию. Процедура измерения этих характеристик и дальнейшее сравнение их измеренных значений осуществляется на базе наличия некоторых признаков и правил сравнения, а также выбора соответствующего метода сравнения.

Рассмотрим возможные методы анализа признака сравнения. Используемые методы сравнения отличаются только процедурой сравнения. В настоящее время достаточно хорошо проработаны и используются в практике принятия решений следующие процедуры сравнения: ранжирование, парное сравнение, оценка, последовательное сравнение и некоторые другие.

Метод ранжирования представляет собой процедуру, предполагающую упорядочение объектов в порядке их предпочтения (предшествования) на основе сравнения их свойств объектов. Для анализа этих свойств вводятся отношения: предпочтения « > » и эквивалентности « ~ ». Если на множестве объектов А ={a1,a2,….,аn} определено только отношение предпочтения « > », то говорят, что задан строгий порядок.

Метод парного сравнения заключается в установлении предпочтения объектов при сравнении только пары объектов. Например, пары объектов а и b возможны следующие ситуации: a>b, ( а предпочтительнее, чем b), а = b, (a эквивалентно b), a < b, ( a не предпочтительнее, чем b). Результаты парных сравнений всегда можно представить в виде матрицы парных сравнений.

Метод последовательного сравнения используется в случае, когда имеется оценка каждого объекта приоритетного сравнения, желательно представленная в нормированных единицах.

Процедура последовательного сравнения состоит из следующих этапов:

1. Ранжирование объектов.

2. Оценка объектов (принимаем, что f(x1)=1 для f=[0,1]).

3. Решение анализа (анализа того, будет ли объект (x1) превосходить все другие объекты, вместе взятые).

При измерении характеристик, оцениваемых как количественных, так и в качественных шкалах, а также при анализе согласованности характеристик используются специальные методы нормирования.

Метод непосредственной (аналитической) оценки. Данный метод основывается на присвоении каждому объекту некоторой вычисленной формально или эвристической оценки, отражающей его количественную характеристику, т.е. задается абсолютное или относительное значение интегральной характеристики объекта на некотором числовом отрезке. Например на отрезке [0:1], объектам ai и aj присвоены оценки

fi = с(ai)=0,2…, fj = c(aj) = 0,1 и т.д.

3. практическое решение задач принятия решений

Одним из наиболее широко известных групп задач данного класса являются задачи, имеющие обобщенное название – оптимизационные задачи. Приведем пример решения задачи.

Задача оптимизации прибыли. Фирма, специализирующаяся на производстве расфасованных орешков, выпускает три различных продукта (продукт 1, продукт 2 и продукт 3), каждый из которых получается путем определенной обработки ореха и подлежит соответствующей упаковке. В начале технологического процесса необработанный орех сортируется по размеру и качеству, после чего его распределяют по различным поточным линиям.

Фирма может закупить орех у двух различных поставщиков. При этом объемы продуктов 1, 2 и 3, которые можно получить из одной тонны ореха первого поставщика, отличаются от объемов продуктов 1, 2 и 3, получаемых из того же количества ореха второго поставщика. Соответствующие показатели приведены в табл. 7.

Исходные данные по задаче. Из данной таблицы следует, что из 1 т ореха поставщика 1 можно изготовить 0,2 т продукта 1, 0,2 т продукта 2 и 0,3 т продукта 3; остальные 0.3 m составляют отходы. У ореха поставщика 2 аналогичные показатели по отношению к продукту 3 и к отходам совпадают с соответствующими показателями для предыдущего случая; однако процент выхода продукта 1 во втором случае оказывается более высоким.

Необходимо определить, какое количество ореха следует купить у каждого из поставщиков. Для ответа необходимо знать «относительную» прибыль, получаемой фирмой в случае покупки ореха у поставщика 1 и у поставщика 2. При этом относительная прибыль при покупке ореха у поставщика 1 вычисляется путем вычитания из полной выручки в результате продажи фирмой всех видов продуктов, полученных из 1 т. необработанного ореха, закупленного у поставщика 1, стоимости 1 т ореха. Аналогично определяется относительная прибыль фирмы, получаемая за счет покупки ореха у поставщика 2. Цены на орех у поставщика 1 и у поставщика 2 могут быть разными.

Термин относительная прибыль используется постольку, поскольку в расчетах пока не принимаются другие виды расходов. К их числу могут, в частности, относиться затраты, связанные с доставкой продукции к местам сбыта и с обслуживанием покупателей. Такого рода затраты имеют место лишь после получения готовой продукции, и считаем что они одинаковы для поставщиков. Они не имеют отношения к затратам во время покупки ореха, и, следовательно, при принятии решения размещение поставщиков ореха не учитывается. Предположим, что относительная прибыль при закупке ореха у поставщика 1 равна 5, а при закупке картофеля у поставщика 2 составляет 6. Из того факта, что относительная прибыль при закупке ореха у поставщика 2 является более высокой, однако, вовсе не следует, что фирме следует произвести закупку всего требуемого ей количества ореха у поставщика 2.

При принятии решения по закупке ореха возможны три основных варианта: либо все закупить у поставщика 1; либо у поставщика 2; либо выявить доли объемов продукции закупаемых у поставщиков. При этом, необходимо учесть следующие факторы: максимальное количество каждого продукта, которое фирма может продать, и максимальное количество каждого из продуктов, которое фирма может изготовить при заданных условиях производства. Для простоты изложения допустим, что, учитывая оба эти фактора одновременно, мы получаем следующие ограничения:

- продукт 1 не может выпускаться в количестве, превышающем 1.8;

- продукт 2 не может выпускаться в количестве, превышающем 1.2;

- продукт 3 не может выпускаться в количестве, превышающем 2,4.

Эти ограничения математически можно сформулировать следующим образом.

Пусть P1 и Р2 означают количество ореха, которое будет закуплено у поставщиков 1 и 2 соответственно. Тогда значения Р1 и Р2 должны подчиняться следующим линейным неравенствам:

0,2Р1 + 0,3Р2 1.8 для продукта 1,

0,2Р1 + 0,1Р2 1.2 для продукта 2, (1)

0,3Р1 + 0,3Р2 2.4 для продукта 3,

P1 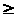0,

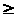P2 0.

Условия неотрицательности P1 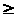0 и P2 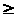0 приняты потому, что отрицательные значения этих величин (например P1 = -4) не имели бы физического смысла.

На основании системы (1) построим предельные линии ограничения. Для этого по каждому из уравнений

0,2Р1 + 0,3Р2 = 1.8

0,2Р1 + 0,1Р2 = 1.2

0,3Р1 + 0,3Р2 = 2.4

дадим значения крайних координат линии ограничения. Например, для уравнения

0,2Р1 + 0,3Р2 = 1.8 имеем Р1 = 0, тогда Р2 = 1.8 : 0.3 = 6. Для Р2 = 0, Р1 = 1.8 : 0.2 = 9.

Аналогично найдем нулевые координаты для других уравнений. Линии ограничения построены на графиках, приведенных на рис.1

Стрелка, проведенная от каждой из этих линий, указывает направление, определяемое знаком неравенства в соответствующем ограничении. Для нахождения совместного решения, совместим линии ограничения на одном графике (рис.2), которые характеризуют допустимые стратегии закупок.

Заштрихованная область является совместной областью для системы (1), значения из которой удовлетворяют условиям ограничения. Все значения Р1 и P2 удовлетворяющие условиям (1), представлены на рис.6 заштрихованной областью.

При этом необходимо сформулировать условие оптимизации и построить целевую функцию решения задачи. Оптимальными являются такие значения P1 и Р2, при которых относительная прибыль максимальна, если при этом выполняются условия (1). Таким образом, задача оптимизации сводится к максимизации выражения

5Р1 + 6Р2  max, (2)

при наличии ограничений (1).

Каждая из множества параллельных прямых, изображенных на этом рисунке, соответствует различным комбинациям значений P1 и Р2, приводящим к одному и тому же значению линейной целевой функции

5Р1 + 6Р2.

Самая верхняя линия, содержащая точку в области допустимых с точки зрения условий (1) значений, определяет максимальное значение целевой функции. Оптимальное решение задается именно этой точкой.

Легко убедиться графически. что в рассматриваемом случае оптимальное решение является единственным; оно находится на пересечении прямых, определяемых двумя первыми условиями (1). Следовательно, оптимальные значения Р1 и Р2 можно вычислить путем совместного решения двух линейных уравнений

0,2Р1 + 0,3Р2 = 1,8 для продукта 1,

0,2Р1 + 0,1Р2 = 1,2 для продукта 2. (3)

Решая данную систему линейных уравнений методом подстановки или Жордана - Гаусса можно определить, что оптимальные значения Р1 = 4,5, а Р2 = 3. Тогда значение целевой функции принимает значение 40,5.

Задача JA – класса (неструктурированные критерии)

Данная группа задач может быть еще разбита на две подгруппы, связанные с количеством используемых критериев и их возможной взаимосвязью.

Для группы с небольшим количеством невзаимосвязанных целей (критериев) используется методология решения основанная на использовании различных стратегий ЛПР относительно получения результатов решения. К ним можно отнести методы: оптимизма, пессимизма (гарантированного результата), Гурвица, Сэвиджа. Рассмотрим методику решения данной группы задач.

Пример задачи JA – класса. Рассмотрим задачу выбора наилучшей структуры объема закупок оптовой компанией продукции для реализации по торговым предприятиям.

Для выбора продукции относящейся к алкогольной, были сформулированы несколько целевых критериев: - оптовая цена, (руб.), (А_>1>); - срок хранения, (кол-во дней) , (А_>2>); - ассортимент торговой марки (шт), (А_>3>).

Выбор производится из следующих видов продукции, предлагаемых предприятиями-поставщиками: Долина (Y_>1>); Фанагория (Y_>2>); Славянский (Y_>3>).

Исходные данные по задаче приведены в табл.9.

Таблица 9

Обобщенная постановка задачи

Альтернативы	Критерии (цели)
А_>1>	А_>2>	А_>3>
Y_>1>	1	8	4
Y_>2>	4	2	5
Y_>3>	6	5	3

1. Принцип максимина (гарантированного результата)

Принцип максимина заключается в выборе в качестве наиболее эффективной той альтернативы (стратегии), которая имеет наибольшее среди наименьших по всем альтернативам значение функции полезности или фактора. Данная стратегия ориентирована на получение гарантированного минимума желательности (не хуже чем "лучший из худших").

Рассмотрим действие принципа максимина на задаче. В соответствии с решающим правилом, оптимальной (u(y*)) считается альтернатива, для которой выполняется соотношение

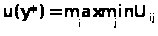
Методика выбора включает в себя два этапа.

На первом - для каждой альтернативы выбираем по соответствующей строке минимальное значение функции полезности. Для альтернативы Y_>1> минимальное из значений 1, 8, 4 является значение функции полезности f_>1>= 1 соответствующее критерию А_>1>; для альтернативы Y_>2> минимальное из значений 4, 2 ,5 является значение функции полезности U_>2>= 2 соответствующее критерию А_>2>; для альтернативы Y_>3> минимальное из значений 6, 7, 3 является значение функции полезности U_>3>= 3 соответствующее критерию А_>3.>Тогда имеем следующие минимальные значения полезности по каждой альтернативе, соответственно:

На втором этапе из полученных минимальных значений проводится выбор максимального:

Максимальной из существующих минимальных является значение = 3, которое соответствует третьей альтернативе. Таким образом, оптимальной (по критерию максимина) является альтернатива Y_>3>.

2. Принцип оптимизма.

При решении задач, относящихся к простым задачам и имеющим четкую структуризацию, обычно применяют некоторый спектр методов, одним из которых является принцип оптимизма. Структуризация проблемной ситуации состоит в исследовании и анализе структуры элементов проблемы, установлении взаимосвязи между ними, решаемой проблемой и другими проблемами, предшествующими данной, т.е. исходная проблема разбивается на составные части и упорядочивается.

Принцип оптимизма заключается в выборе в качестве наиболее эффективной той альтернативы (стратегии), которая имеет наибольшее из наибольших по всем альтернативам значение функции полезности или фактора, т.е. принцип оптимизма (по правилу «лучший из лучших») учитывает возможность получения максимального уровня желательности. Эта стратегия реализуется решающим правилом вида:

u(y*) = max max U_>ij>.

i j

Проведем решение исходной задачи (табл.9 ) с использованием данной методики.

Решение задачи по принципу оптимизма.

На первом этапе для каждой альтернативы выбираем максимальное значение по соответствующей строке.

Для альтернативы Y_>1> минимальное из значений 1, 8, 4 является значение 8 соответствующее критерию А_>2>; для альтернативы Y_>2> минимальное из значений 4, 2, 5 является значение 5 соответствующее критерию А_>3>; для альтернативы Y_>3> минимальное из значений 6, 5 ,3 является значение 7 соответствующее критерию А_>1.>

На втором этапе из уже полученных максимальных значений выбирается максимальное:

Оптимальной (по критерию оптимизма) является альтернатива Y_>1>.

3. Принцип Гурвица.

Для принципа выбора Гурвица характерно использование взвешенных значений принципа гарантированного результата (пессимизма) и принципа оптимизма. Здесь каждая стратегия характеризуется своим коэффициентом важности стратегии α,β = [0,1]. Функция выбора, описывающая принцип Гурвица, может быть записана в виде:

u (y*)= α·u_>1>(y)+(1-α)·u_>2>(y),

где u_>1>(y) - стратегия выбора, характеризующая принцип гарантированного результата;

u_>2>(y) - стратегия выбора, характеризующая принцип оптимизма.

Учитывая, что

u_>1>(y) = max min U _{>i j}>

i j

u_>2>(y) = max max U _{>i j}>

i j

можно представить общее выражение для принципа Гурвица в виде

u (y*)= α max min U _{>i j}> + (1-α)· max max U _{>i j}> (3)

i j i j

или

u (y*)= max [α min U _{>i j}> + (1-α)· max U _{>i j}> ]. (4)

i j j

Следовательно, наиболее предпочтительна стратегия Y*, для которой выполняется условие (4). При этом в зависимости от значения весового коэффициента α можно получить различные стратегии выбора при изменении его в диапазоне 0 ≤ α ≤ 1:

если α = 1, то получим принцип гарантированного результата;

если α = 0, получим принцип оптимизма.

Проведем решение исходной задачи (табл.9)с использованием данной методики.

Решение задачи по принципу Гурвица.

Задаём коэффициент , который характеризует ориентацию на принцип максимина или принцип оптимизма и     . Пусть  = 0,6.
Решаем задачу по формуле Y^* max_>i> ( min U_>ij>_>>+ (1 - ) max_>j> U_>ij>) в два этапа:

2.1. Для каждой альтернативы находим *min_>j> U_>ij>_>>+(1-)* max_>j> U_>ij> , для чего используем уже вычисленные значения по предыдущим задачам (значения Min U_>ij>, Max U_>ij>_>>в табл.10). Расчет этих значений формируется так.

Исходными данными для выбора по методу Гурвица будут данные, полученные по стратегиям:

- для стратегии гарантированного результата:

- для стратегии оптимизма:

_>>Принцип Гурвица Таблица 10

Альтернати- вы Yi	Критерии (цели)	Знач. предпочт. по Гурвицу	Весовой коэф-т
A1	A2	A3	Min U_>ij>	Max U_>ij>
Y1	1	8	4	1	8	3,8	0,6
Y2	4	2	5	2	5	3,2	0,6
Y3	6	5	3	3	6	4,2	0,6
min	1	2	3		5
max	6	8	5	3		4,2

Пусть весовой коэффициент характеризует степень важности соответствующей первой стратегии и его значение примем  = 0,6. Тогда получим для первого этапа

Подставляя соответствующие значения в систему получим:

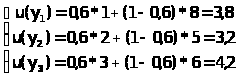
Подставим их в графу «Значение предпочтений по Гурвицу» табл.10.

2.2. На втором этапе производим выбор в соответствии с правилом :

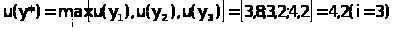
Оптимальной (по комбинированному принципу Гурвица) будет альтернатива Y_>3>, значение функции полезности которой равно 4,2.

Для оценки влияния коэффициента  на уровень предпочтений по Гурвицу, проведем анализ значений для различных коэффициентов (табл.11).

Таблица 11

Значения предпочтений по Гурвицу для различных коэффициентов 

	возможные значения весового коэффициента а
	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
Y1	7,3	6,6	5,9	5,2	4,5	3,8	3,1	2,4	1,7
Y2	4,7	4,4	4,1	3,8	3,5	3,2	2,9	2,6	2,3
Y3	5,7	5,4	5,1	4,8	4,5	4,2	3,9	3,6	3,3
Y*	7,3	6,6	5,9	5,2	4,5	4,2	3,9	3,6	3,3	7,3

На основании данных значений можно сказать, что общим правилом выбора по всем значениям  будет метрика с  = 0,1, при этом, эффективной альтернативой является вариант 1 (Y1) с функцией предпочтения = 7,3.

Решение данной задачи в интегрированной системе Excel предполагает процедуру расчета показателей приведенных в табл.10-11, по алгоритму и формулам, приведенным в табл.12 и табл.13. Экранная форма указанных таблиц приведена на рис.10, 11.

Алгоритм расчета показателей по принципу Гурвица, в виде экранной формы приведен на рис.12.

4. Принцип Сэвиджа (принцип минимаксного сожаления ).

Стратегия выбора основанная на использовании стратегии Сэвиджа характеризуется теми потенциальными потерями, которые ЛПР может иметь, если выберет неоптимальное решение. Процедура выбора обычно происходит в три этапа и строится на вычислении промежуточного показателя функции потерь (w) на базе имеющихся для каждой альтернативы функции полезности (.U_>ij>).

На первом этапе для каждого критерия A_>j> по конкретной альтернативе y_>i> определяется максимальное значение функции полезности .

max U_>ij>= max U_>i> │ A_>j> ,

i i

показывающей возможный наилучший уровень полезности U_>i>, который можно получить, для конкретного критерия A_>j>_>>.

На втором этапе, на основании полученных значений для каждой альтернативы строится показатель

w (y_>1>) │A_>j> = w(y_>ij>) = max U_>ij> -U_>ij>

характеризующий потенциальный риск (потерянную выгоду от выбора неоптимальной альтернативы).

На третьем этапе производится выбор стратегии с наименьшим показателем риска :

u (y* ) = min w(y_>ij>_>>)

Проведем решение исходной задачи (табл. 9) с использованием данной методики.

Решение задачи по принципу Сэвиджа.

На первом этапе для каждого критерия А_>j>_>>по конкретной альтернативе Y_>i> определяется максимальное значение:

Данные значения приведены в табл. 10 в строке «max».

На втором этапе на основе полученных значений для каждой альтернативы строится показатель, характеризующий потенциальный риск.

Если для первого критерия А_>1> руководство предприятием выбрало стратегию Y_>3,>то значение потерь равно:

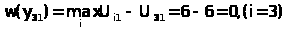
Если для первого критерия А_>1> руководство предприятием выбрало стратегию Y_>1,>то значение потерь равно:

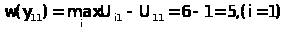
Если для первого критерия А_>1> руководство предприятием выбрало стратегию Y_>2,>то значение потерь равно:

Для второго критерия А_>2> максимальной является альтернатива Y_>1,>при выборе ее руководство имеет минимальные потери: w(y_>12>)=0.

Если для первого критерия А_>2> руководство предприятием выбрало стратегию Y_>2,>то значение потерь равно:

Если для первого критерия А_>2> руководство предприятием выбрало стратегию Y_>3,>то значение потерь равно:

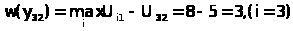
Для второго критерия А_>3> максимальной является альтернатива Y_>2,>при выборе ее руководство имеет минимальные потери: w(y_>23>)=0.

Если для первого критерия А_>3> руководство предприятием выбрало стратегию Y_>1,>то значение потерь равно:

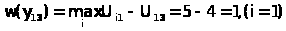
Если для первого критерия А_>3> руководство предприятием выбрало стратегию Y_>3,>то значение потерь равно:

На основании полученных данных строится матрица сожалений (табл.14).

Таблица 14

Матрица сожалений

Альтернативы	Критерии (цели)
А_>1>	А_>2>	А_>3>
Y_>1>	5	0	1
Y_>2>	2	6	0
Y_>3>	0	3	2

На основании матрицы потерь можно определить максимальные потери по каждой альтернативе.

Оптимальной будет та альтернатива, которая имеет минимальные потери, т.е.

Таким образом, оптимальной здесь представляется альтернатива Y_>3,>имеющая минимальные потери выгоды. На рис.13 представлена экранная форма решающих матриц по принципу Сэвиджа.

Алгоритм и формулы реализации решающих таблиц представлены в табл.15-18.

Таблица 15

Алгоритм формирования матриц для обобщенной постановки задачи

	A	B	C	D
2	Альтернативы		Критерии (цели)
3	A1	A2	A3
4	Y1	1	8	4
5	Y2	4	2	5
6	Y3	6	5	3
7	max_>j>	=МАКС(B4:B6)	=МАКС(C4:C6)	=МАКС(D4:D6)

Таблица 16Расчетная матрица формирования потенциальных потерь wij

	A	B	C	D	E
11	Альтернативы	Критерии (цели)	max_>j>
12	A1	A2	A3
13	Y1	=$B$7-B4	=$C$7-C4	=$D$7-D4	=МАКС(B13:D13)
14	Y2	=$B$7-B5	=$C$7-C5	=$D$7-D5	=МАКС(B14:D14)
15	Y3	=$B$7-B6	=$C$7-C6	=$D$7-D6	=МАКС(B15:D15)
				min_>i>	=МИН(E13:E15)

Задачи JA – класса (неструктурированные критерии), решаемую методом «смещенного идеала»

Пример задачи JA – класса с неструктурированными критериями:(метод «смещенного идеала»).

Постановка задачи. Осуществить закупку наиболее эффективного варианта принтера, удовлетворяющего потребительским качествам. Определим параметры решения задачи.

Время для ПР: Т=2 недели.
Ресурсы для ПР: информация о характеристиках принтеров.
Критерии потребительского выбора {К}:

К_>1> - скорость печатающего механизма в монохромном режиме, страниц в минуту

К_>2> - ОЗУ, установлено/максимум, Мбайт

К_>3> - цена принтера.

Множество ограничений (В)

- на финансовые ресурсы;

- развитие сервисных служб.

Множество альтернативных вариантов – предлагаемые производителями марки принтеров различных типов.

Решение задачи методом «идеального объекта».

Этап расчета 1. На предварительном этапе отобранная группа принтеров, состоящая из 7 типов принтеров Y={А_>1>, А_>2>, А_>3>, А_>4>, А_>5>, А_>6>, А_>7>}. На основании исходных данных строим матрицу вариантов (табл.17)

Таблица 17

Матрица описания задачи

Принтеры	Критерии
К _>1>	К _>2>	К _>3>
А _>1>	12	12	4854
А _>2>	8	3	3442
А _>3>	7	4	2776
А _>4>	9	2	4270
А _>5>	11	8	4450
А _>6>	14	6	5830
А _>7>	10	8	4667

На основании данных приведенных в таблице сформируем «идеальный объект» по указанным критериям со значениями равными максимальным значениям показателей, полезность по которым возрастает, и минимальным полезность по которым убывает. Таким образом, получаем «идеальный объект» А⁺:

А⁺  14; 2; 2776

Кроме идеального объекта сформируем также модель «наихудшего объекта»:

А^-  7; 12; 5830

Для сопоставления значений критериев необходимо перейти к нормированным единицам, т.к. критерии разнородные, преобразовав их по формуле

_>j>_>>= (К⁺-К_>j>) / (К⁺- К^-).

Переходя к относительным значениям критериев, получим следующую нормализованную матрицу (табл18):

Таблица 18

Нормализованная матрица описания задачи

Принтеры	Критерии
К _>1>	К _>2>	К _>3>
А _>1>	0,29	1	0,68
А _>2>	0,86	0,1	0,22
А _>3>	1	0,2	0
А _>4>	0,71	0	0,49
А _>5>	0,43	0,6	0,55
А _>6>	0	0,4	1
А _>7>	0,57	0,6	0,62

Зададим относительную важность критериев в виде весов: W_>1>= 6, W_>2>= 2, W_>3>= 4.

Для выявления ненаилучших объектов найдем свертки (расстояние до идеального объекта), используя следующую обобщенную метрику:

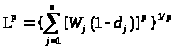
Вычислим для наших объектов метрики с разной степенью концентрации, соответствующие различным стратегиям выбора, и значения запишем в таблицу (табл.19).

Таблица 19

Метрика расстояний по альтернативам

Значения меры расстояния	Степень концентрации (р)
р=1	р=2	р=3	р=5	р=6	р=8
L(А_>1>)	5,56	4,47	4,32	4,29	4,29	4,29
L(А_>2>)	5,78	3,71	3,33	3,17	3,15	3,13
L(А_>3>)	5,60	4,31	4,08	4,01	4,00	4,00
L(А_>4>)	5,76	3,33	2,78	2,42	2,34	2,24
L(А_>5>)	6,04	3,96	3,60	3,46	3,44	3,43
L(А_>6>)	7,20	6,12	6,02	6,00	6,00	6,00
L(А_>7>)	4,89	3,09	2,76	2,61	2,59	2,58

Чем больше значение L, тем ближе объект А_>i> к идеальному А⁺. Получим следующие ранжировки предпочтений по L.

Для р=1 А_>6>А_>5>А_>2>А_>4>А_>3>А_>1>А_>7>

Для р=2 А_>6>А_>1>А_>3>А_>5>А_>2>А_>4>А_>7>

Для р=3 А_>6>А_>1>А_>3>А_>5>А_>2>А_>4>А_>7>

Для р=5 А_>6>А_>1>А_>3>А_>5>А_>2>А_>7>А_>4>

Для р=6 А_>6>А_>1>А_>3>А_>5>А_>2>А_>7>А_>4>

Для р=8 А_>6>А_>1>А_>3>А_>5>А_>2>А_>7>А_>4>.

Ненаилучшие решения в нашем случае – А_>4> и А_>7>. Исключим их из рассмотрения, получив сокращенное исходное множество альтернатив А_>1>, А_>2>, А_>3>, А_>5>, А_>6>.

Рассмотрим компьютерное решение данного фрагмента задачи в системе Excel.

Экранная форма комплекса таблиц расчета по первому этапу приведена на рис.14.

Алгоритм формирования матрицы описания задачи и расчета нормализованной матрицы приведены по 1 этапу приведены в табл.20-21. В данных таблицах приводятся формулы выбора экстремальных уровней критериев по каждой альтернативе (в табл. 20, в координатах граф и строк, это - диапазон B12:D12 для выбора значений идеального варианта, B13:D13 – для выбора значений наихудшего варианта). В табл.21 приводятся формулы расчета нормализованных значений критериев по альтернативам.

Таблица 20

Матрица описания задачи

	А	B	C	D
3	Принтеры	Критерии
4	К _>1>	К _>2>	К _>3>
5	А _>1>	12	12	4854
6	А _>2>	8	3	3442
7	А _>3>	7	4	2776
8	А _>4>	9	2	4270
9	А _>5>	11	8	4450
10	А _>6>	14	6	5830
11	А _>7>	10	8	4557
12	идеальный объект А+	=МАКС(B5:B11)	=МИН(C5:C11)	=МИН(D5:D11)
13	наихудший объект А-	=МИН(B5:B11)	=МАКС(C5:C11)	=МАКС(D5:D11)

Таблица 21.

Нормализованная матрица описания задачи

	А	B	C	D
17
18	К1	К2	К3
19	А1	=(B12-B5)/(B12-B13)	=(C12-C5)/(C12-C13)	=(D12-D5)/(D12-D13)
20	А2	=(B12-B6)/(B12-B13)	=(C12-C6)/(C12-C13)	=(D12-D6)/(D12-D13)
21	А3	=(B12-B7)/(B12-B13)	=(C12-C7)/(C12-C13)	=(D12-D7)/(D12-D13)
22	А4	=(B12-B8)/(B12-B13)	=(C12-C8)/(C12-C13)	=(D12-D8)/(D12-D13)
23	А5	=(B12-B9)/(B12-B13)	=(C12-C9)/(C12-C13)	=(D12-D9)/(D12-D13)
24	А6	=(B12-B10)/(B12-B13)	=(C12-C10)/(C12-C13)	=(D12-D10)/(D12-D13)
25	А7	=(B12-B11)/(B12-B13)	=(C12-C11)/(C12-C13)	=(D12-D11)/(D12-D13)
26	W (важность критерия)	6	2	4

В табл.22 приводятся формулы расчета расстояния по нормализованным значениям для различных степеней концентрации, в частности, для р = 2, имеем Евклидово расстояние. В строке 31 дается линейка коэффициентов концентрации от 1 до 8.

Этап расчета 2. На втором этапе, по усеченному множеству альтернатив (табл.23) опять строим идеальный А⁺ и наихудший А^- варианты.

Таблица 23

Матрица описания задачи

по сокращенному множеству альтернатив

Принтеры	Критерии
К _>1>	К _>2>	К _>3>
А _>1>	12	12	4854
А _>2>	8	3	3442
А _>3>	7	4	2776
А _>5>	11	8	4450
А _>6>	14	6	5830

Значение параметров крайних альтернатив следующие:

Принтеры	Критерии
К _>1>	К _>2>	К _>3>
идеальный объект А+	14	3	2776
наихудший объект А-	7	12	5830

Для сопоставления значений критериев также необходимо перейти к нормированным единицам, т.к. критерии разнородные, опять преобразовав их по формуле

_>j>_>>= (К⁺-К_>j>) / (К⁺- К^-).

Переходя к относительным значениям критериев, получим новую нормализованную матрицу (табл.24).

Таблица 24

Нормализованная матрица описания задачи

по сокращенному множеству альтернатив

Принтеры	Критерии
К _>1>	К _>2>	К _>3>
А _>1>	0,29	1	0,68
А _>2>	0,86	0	0,22
А _>3>	1	0,11	0
А _>5>	0,43	0,56	0,55
А _>6>	0	0,33	1

Также зададим относительную важность критериев в виде весов: W_>1>=6, W_>2>=2, W_>3>=4.

Для выявления не наилучших объектов найдем свертки (расстояние до идеального объекта), используя метрику:

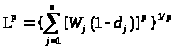
Вычислим для наших объектов разные метрики, соответствующие различным стратегиям выбора, и значения запишем в таблицу (табл.25).

Таблица 25

Метрика расстояний по альтернативам

Значения меры расстояния	Степень концентрации (р)
р=1	р=2	р=3	р=5	р=6	р=8
L(А_>1>)	5,56	4,47	4,32	4,29	4,29	4,29
L(А_>2>)	5,98	3,81	3,40	3,19	3,16	3,14
L(А_>3>)	5,78	4,38	4,11	4,01	4,01	4,00
L(А_>5>)	6,12	3,98	3,61	3,46	3,44	3,43
L(А_>6>)	7,33	6,15	6,02	6,00	6,00	6,00

Чем больше значение L, тем ближе объект А_>i> к идеальному А⁺. Получим следующие ранжировки предпочтений по L.

Для р=1 А_>6>А_>5>А_>2>А_>3>А_>1>

Для р=2 А_>6>А_>1>А_>3>А_>5>А_>2>

Для р=3 А_>6>А_>1>А_>3>А_>5>А_>2>

Для р=5 А_>6>А_>1>А_>3>А_>5>А_>2>

Для р=6 А_>6>А_>1>А_>3>А_>5>А_>2>

Для р=8 А_>6>А_>1>А_>3>А_>5>А_>2>

Ненаилучшие решения в нашем случае – А_>2> и А_>5>. Исключим их из рассмотрения, получив сокращенное исходное множество А_>1>, А_>3>, А_>6>. Рассмотрим компьютерное решение данного фрагмента (2 уровня) решения задачи в системе Excel.

Экранная форма комплекса таблиц расчета по второму этапу приведена на рис.15.

Алгоритм формирования матрицы описания усеченной задачи и расчета нормализованной матрицы приведены по 2 этапу приведены в табл.26-27. В данных таблицах приводятся формулы выбора экстремальных уровней критериев по каждой альтернативе (в табл. 26, в координатах граф и строк, это - диапазон B10:D10 для выбора значений идеального варианта, B11:D11 – для выбора значений наихудшего варианта). В табл.27 приводятся формулы расчета нормализованных значений критериев по альтернативам.

Таблица 26

Матрица описания задачи (2 этап)

	A	B	C	D
3	Принтеры	Критерии
4	К _>1>	К _>2>	К _>3>
5	А _>1>	12	12	4854
6	А _>2>	8	3	3442
7	А _>3>	7	4	2776
8	А _>5>	11	8	4450
9	А _>6>	14	6	5830
10	идеальный объект А+	=МАКС(B5:B9)	=МИН(C5:C9)	=МИН(D5:D9)
11	наихудший объект А-	=МИН(B5:B9)	=МАКС(C5:C9)	=МАКС(D5:D9)

Таблица 27.

Нормализованная матрица описания задачи

	A	B	C	D
14
15	К _>1>	К _>2>	К _>3>
16	А1	=(B10-B5)/(B10-B11)	=(C10-C5)/(C10-C11)	=(D10-D5)/(D10-D11)
17	А2	=(B10-B6)/(B10-B11)	=(C10-C6)/(C10-C11)	=(D10-D6)/(D10-D11)
18	А3	=(B10-B7)/(B10-B11)	=(C10-C7)/(C10-C11)	=(D10-D7)/(D10-D11)
19	А5	=(B10-B8)/(B10-B11)	=(C10-C8)/(C10-C11)	=(D10-D8)/(D10-D11)
20	А6	=(B10-B9)/(B10-B11)	=(C10-C9)/(C10-C11)	=(D10-D9)/(D10-D11)
21	W (важность критерия)	6	2	4

В табл.28 приводятся формулы расчета расстояния по нормализованным значениям усеченной матрицы альтернатив для различных степеней концентрации.

Этап расчета 3. На третьем этапе также строим идеальный А⁺ 14; 4; 2776 и наихудший А^-  7; 12; 5830 варианты уже по усеченному множеству (до 3) альтернатив (табл.29).

Таблица 29

Матрица описания задачи по сокращенному множеству альтернатив

Принтеры	Критерии
К_>1>	К_>2>	К_>3>
А_>1>	12	12	4854
А_>3>	7	4	2776
А_>6>	14	6	5830

Определяем значения параметров крайних альтернатив:

Принтеры	Критерии
К _>1>	К _>2>	К _>3>
идеальный объект А+	14	4	2776
наихудший объект А-	7	12	5830

_>j>_>>= (К⁺-К_>j>) / (К⁺- К^-).

Переходя к относительным значениям критериев, получим новую нормализованную матрицу (табл.30).

Таблица 30

Нормализованная матрица описания задачи по сокращенному множеству альтернатив

Принтеры	Критерии
К_>1>	К_>2>	К_>3>
А_>1>	0,29	1	0,68
А_>3>	1	0	0
А_>6>	0	0,25	1

Опять зададим относительную важность критериев в виде весов:W_>1>= 6, W_>2>= 2, W_>3>=4.

Для выявления ненаилучших вариантов найдем метрические свертки (расстояние до идеального варианта), используя следующую метрику:

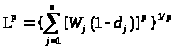
Вычислим для наших объектов разные метрики, соответствующие различным стратегиям выбора, и значения запишем в таблицу (табл.31).

Таблица 31

Метрика расстояний по сокращенному количеству альтернативам

Значения меры расстояния	Степень концентрации (р)
р=1	р=2	р=3	р=5	р=6	р=8
L(А_>1>)	5,56	4,4723	4,32	4,29	4,29	4,29
L(А_>3>)	6,00	4,4721	4,16	4,02	4,01	4,00
L(А_>6>)	7,50	6,18	6,03	6,00	6,00	6,00

Чем больше значение L, тем ближе объект А_>i> к идеальному А⁺. Получим следующие ранжировки предпочтений по L.

Для р=1 А_>6>А_>3>А_>1>

Для р=2 А_>6>А_>1>А_>3>

Для р=3 А_>6>А_>1>А_>3>

Для р=5 А_>6>А_>1>А_>3>

Для р=6 А_>6>А_>1>А_>3>

Для р=8 А_>6>А_>1>А_>3>

Ненаилучшие решения в нашем случае – А_>1> и А_>3>. Остался один доминирующий объект А_>6>, т.е. это и есть наилучшее решение в нашей ситуации.

Компьютерное решение данного фрагмента (3 уровня) решения приведено на рис.16.

Алгоритм формирования матрицы описания усеченной до 3 альтернатив задачи и расчета нормализованной матрицы по 3 этапу приведены в табл.32-33. В данных таблицах приводятся формулы выбора экстремальных уровней критериев по каждой альтернативе (в табл. 32, в координатах граф и строк, это - диапазон B8:D8 для выбора значений идеального варианта, B9:D9 – для выбора значений наихудшего варианта). В табл.33 приводятся формулы расчета нормализованных значений критериев по альтернативам.

Таблица 32

Матрица описания задачи (3 этап)

	А	B	C	D
3	Принтеры	Критерии
4	К _>1>	К _>2>	К _>3>
5	А _>1>	12	12	4854
6	А _>3>	7	4	2776
7	А _>6>	14	6	5830
8	идеальный объект А+	=МАКС(B5:B11)	=МИН(C5:C11)	=МИН(D5:D11)
9	наихудший объект А-	=МИН(B5:B11)	=МАКС(C5:C11)	=МАКС(D5:D11)

Таблица 33

Нормализованная матрица описания задачи

	A	B	C	D
12		Критерии
13	К _>1>	К _>2>	К _>3>
14	А1	=(B10-B5)/(B10-B11)	=(C10-C5)/(C10-C11)	=(D10-D5)/(D10-D11)
15	А3	=(B10-B7)/(B10-B11)	=(C10-C7)/(C10-C11)	=(D10-D7)/(D10-D11)
16	А6	=(B10-B9)/(B10-B11)	=(C10-C9)/(C10-C11)	=(D10-D9)/(D10-D11)
17	W (важность критерия)	6	2	4

В табл.34 приводятся формулы расчета расстояния по нормализованным значениям усеченной матрицы альтернатив для различных степеней концентрации.

Заключение

Принятие решения представляет собой генерирование альтернативных решений и определенных действий над множеством альтернатив, в результате которого исходное множество альтернатив сужается. Это действие называется «выбор», которое придает всей управленческой деятельности целенаправленность. Именно через элемент выбора реализуется подчиненность всей деятельности определенной цели или совокупности взаимосвязанных целей. При этом каждому ЛПР приходится участвовать в процессе управления и проводить этап принятия решений, т.е. выбирать и анализировать наиболее перспективные направления развития проблемы и оценивать ее последствия с точки зрения увеличения общей экономической эффективности предприятия, организации. Для реализации выбранной альтернативы в процессе управления необходим еще и этап организации принятия решения.

Решения являются универсальной формой управленческого поведения как отдельной личности, так и социальных групп. Эта универсальность объясняется сознательным и целенаправленным характером человеческой деятельности. Однако, несмотря на универсальность решений, их принятие в процессе управления экономической системой существенно отличается от решений, принимаемых в частной жизни.

Список литературы

Алдокин И.П., Бубенко И.В. Теория принятия решений.Киев: Наук. думка,1990.156 с.
Афоничкин А.И, Михаленко Д.Г. Управленческие решения в экономических системах: Учебник для вузов.- Спб.: Питер, 2009. – 480с.
Афоничкин А.И. Принятие управленческих решений в экономических системах. . Саранск, Изд-во МордГУ, 1998. - 184 с.
Афоничкин А.И. и др. Системы поддержки в теории и практике оценки управленческих решений. Саранск: Изд-во Мордов ун-та, 1995. - 224с.
Дорохов А.А. Теория принятия оперативных решений / МАИ. М., 1989. 40 с.
Евланов Л.Г. Основы теории принятия решений /МИФИ. М,.1979. 78 с.
Емельянов С.В. Многокритериальные методы принятия решений. М.: Наука, 1985. 217 с.
Кини Р., Райфа Х. 0 Принятие решений при многих критериях: предпочтения и замещения. М.: Радио и связь, 1981. 242 с.
Крылова Т.Б. Выбор партнера: анализ отчетности капиталистического предприятия. М.: Финансы и статистика, 1991. 160 с.
Мулен Э. Кооперативное принятие решений: Аксиомы и модели. М.: Мир, 1991. 281 с.
Планкет Л.,Хейл Г. Выработка и принятие управленческих решений. М.: Мир, 1984. 167 с.
Разработка бизнес-приложений в экономике на базе MS EXCEL /Под общей редакц. А.И.Афоничкина. – М.: Диалог-МИФИ, 2003. – 416с.
Теория выбора и ринятия решений\ под ред И.М.Макарова. М.Наука, 1982г . 328с.

14. Фишберн П. Теория полезности для принятия решений. М.: Мир., 1978. 380 с.