Функціональне відображення поведінки споживача
Функціональне відображення поведінки споживача
1. Геометричне подання зміни попиту при зміні доходу й цін
Припустимо змінюється
доход ( ).
Його збільшення або зменшення еквівалентно
паралельному зсуву бюджетної прямої.
Зі зміною доходу змінюється й попит на
товари. На кожній бюджетній прямій можна
знайти точку рівноваги, в якій
забезпечується максимум функції
корисності
).
Його збільшення або зменшення еквівалентно
паралельному зсуву бюджетної прямої.
Зі зміною доходу змінюється й попит на
товари. На кожній бюджетній прямій можна
знайти точку рівноваги, в якій
забезпечується максимум функції
корисності
 .
Нехай цими точками є точки
.
Нехай цими точками є точки
 ,
,
 ,
,
 ,
,
 на рис. 1. З'єднавши їх, одержимо криву
на рис. 1. З'єднавши їх, одержимо криву
 .
Така крива називається кривою
доход-споживання, або кривою Енгеля. На
рис. 1. крива Енгеля відображує зміну
попиту споживача (при зростанні його
доходу) у випадку, коли жоден з товарів
не є малоцінним. За умови, що 1 – малоцінний,
а 2 – цінний товари, крива Енгеля приймає
вигляд, зображений на рис. 2.
.
Така крива називається кривою
доход-споживання, або кривою Енгеля. На
рис. 1. крива Енгеля відображує зміну
попиту споживача (при зростанні його
доходу) у випадку, коли жоден з товарів
не є малоцінним. За умови, що 1 – малоцінний,
а 2 – цінний товари, крива Енгеля приймає
вигляд, зображений на рис. 2.
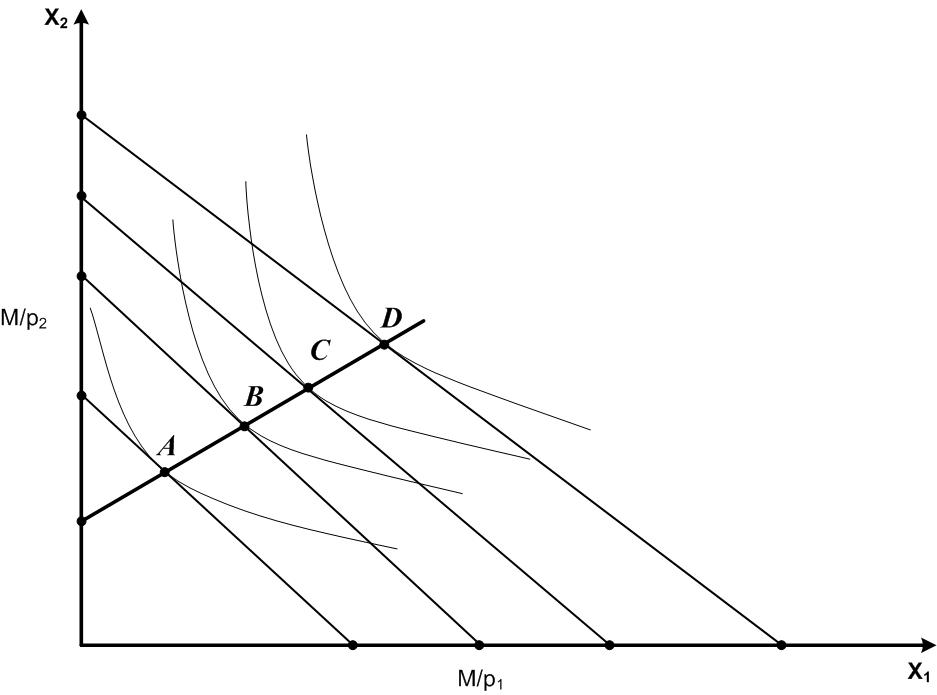

Рисунок 1. Рисунок 2
Припустимо, що змінюється ціна товару 1. Установимо, як змінюється попит на товари 1 і 2. Розглянемо бюджетну пряму (рис. 2)
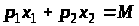 .
.
Нехай
 зменшується. Тоді точка
зменшується. Тоді точка
 переходить у точку
переходить у точку
 ,
а точка
,
а точка
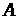 – у точку
– у точку
 – нову точку рівноваги, в якій споживачеві
забезпечується новий максимум функції
корисності
– нову точку рівноваги, в якій споживачеві
забезпечується новий максимум функції
корисності
 .
Зменшимо ціну
.
Зменшимо ціну
 .
Тоді точка
.
Тоді точка
 переміститься в точку
переміститься в точку
 ,
а точка
,
а точка
 займе положення точки
займе положення точки
 й т.д. З'єднавши точки
й т.д. З'єднавши точки
 ,
,
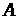 ,
,
 ,
,
 ,
,
 одержимо криву ціни-споживання (або
криву цін) як геометричне місце точок,
які характеризують зміну попиту двох
товарів при зміні ціни
одержимо криву ціни-споживання (або
криву цін) як геометричне місце точок,
які характеризують зміну попиту двох
товарів при зміні ціни
 .
На відміну від лінії доход-споживання,
що виходить із початку координат, лінія
ціна-споживання починається в точці
.
На відміну від лінії доход-споживання,
що виходить із початку координат, лінія
ціна-споживання починається в точці
 .
.

Рисунок 3
Проаналізуємо більш
детально процес переходу з точки
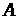 в точку
в точку
 при зміні ціни
при зміні ціни
 (рис. 4). Позначимо вихідну бюджетну лінію
через
(рис. 4). Позначимо вихідну бюджетну лінію
через
 ,
а змінену – через
,
а змінену – через
 .
Проведемо пряму
.
Проведемо пряму
 паралельно прямій лінії цін
паралельно прямій лінії цін
 так, щоб вона мала точку дотику з кривою
байдужності 1. Нехай точкою дотику буде
точка
так, щоб вона мала точку дотику з кривою
байдужності 1. Нехай точкою дотику буде
точка
 .
Як у точці
.
Як у точці
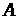 ,
так й у точці
,
так й у точці
 споживачеві забезпечується один і той
самий рівень корисності, оскільки ці
точки належать одній кривій байдужності.
Перехід із точки
споживачеві забезпечується один і той
самий рівень корисності, оскільки ці
точки належать одній кривій байдужності.
Перехід із точки
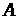 в
в
 розглянемо поетапно: спочатку з
розглянемо поетапно: спочатку з
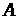 в точку
в точку
 ,
потім із точки
,
потім із точки
 у точку
у точку
 .
Перехід з А в точку В не супроводжується
зміною корисності. Ціна першого товару
знизилася, тому попит на нього зменшився
– відбулася заміна одного товару іншим,
що відповідає ефекту заміни. Перехід
із точки
.
Перехід з А в точку В не супроводжується
зміною корисності. Ціна першого товару
знизилася, тому попит на нього зменшився
– відбулася заміна одного товару іншим,
що відповідає ефекту заміни. Перехід
із точки
 у точку
у точку
 відповідає ефекту доходу й обумовлений
зміною реального доходу при зміні цін.
відповідає ефекту доходу й обумовлений
зміною реального доходу при зміні цін.
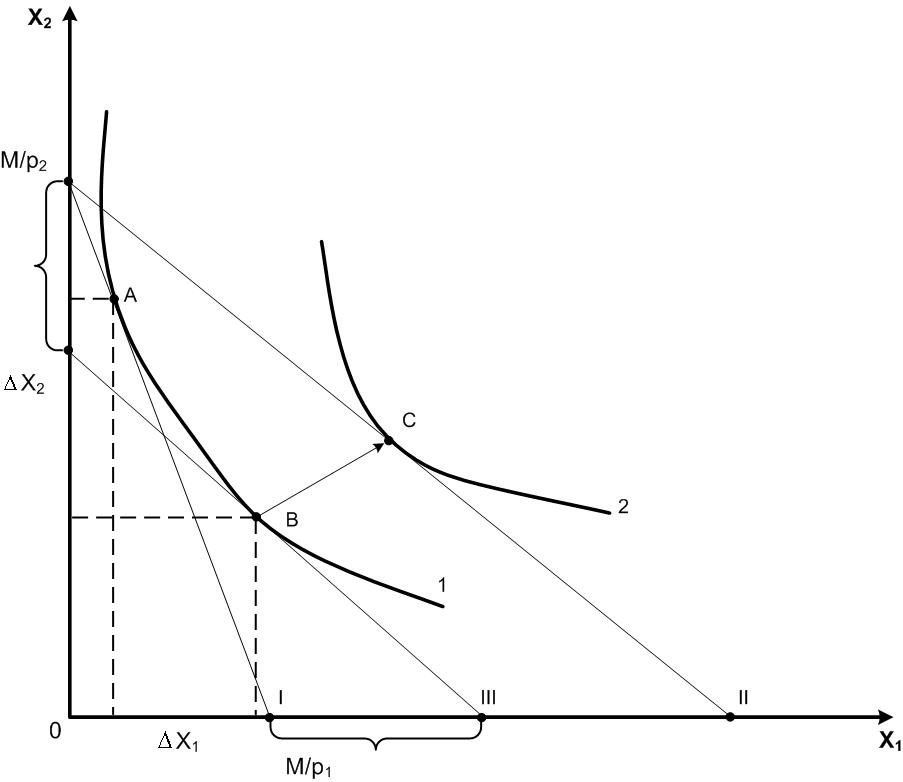
Рисунок 4
2 Аналіз математичної моделі поведінки споживача. Функція попиту споживача
При будь-яких додатних
цінах
 і доході
і доході
 розв’язок задачі поведінку споживача,
існує й єдиний.
розв’язок задачі поведінку споживача,
існує й єдиний.
Очевидно, що цей
розв’язок залежить від
 і
і
 ,
тобто вибір споживача є функцією, що
залежить від цін і доходу. Ця функція
називається функцією попиту
,
тобто вибір споживача є функцією, що
залежить від цін і доходу. Ця функція
називається функцією попиту
 або в розгорнутому вигляді:
або в розгорнутому вигляді:
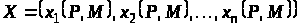 .
.
Цей запис означає, що
при цінах
 і доході
і доході
 вибирається споживчих благ у кількостях
вибирається споживчих благ у кількостях
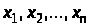 .
.
Основною властивістю
функції попиту є її однорідність щодо
всіх цін і доходу, тобто значення попиту
інваріантні відносно пропорційних змін
 й
й
 :
:
 ,
де
,
де
 .
.
Ця властивість виражає той факт, що вибір споживача залежить тільки від співвідношення цін на товари, а не від масштабу цін.
Аналіз моделі поведінки
споживача полягає у вивченні чутливості
розв’язку до зміни її параметрів
 і
і
 .
Цей підхід у математичній економіці
називається методом
порівняльної статистики.
.
Цей підхід у математичній економіці
називається методом
порівняльної статистики.
Розглянемо задачу, в
якій рівняння являють собою
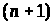 умови першого порядку й можуть бути
розв’язані відносно оптимальних
кількостей усіх продуктів
умови першого порядку й можуть бути
розв’язані відносно оптимальних
кількостей усіх продуктів
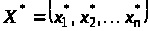 і оптимального множника Лагранжа
і оптимального множника Лагранжа
 ,
тобто розв’язок подається у вигляді
функції попиту
,
тобто розв’язок подається у вигляді
функції попиту
 та функції
попиту та доходу
та функції
попиту та доходу
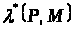 .
Поставимо
.
Поставимо
 й
й
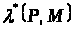 в
в
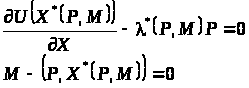
або в розгорнутому вигляді
 (1)
(1)
Позначимо
 і
і
 .
.
Отже
перейдемо до аналізу
математичної моделі поведінки споживача
відносно зміни її параметрів
 і
і
 :
:
1.
Розглянемо вплив зміни доходу
 на розв’язок задачі споживання. Для
цього продиференцюємо (1) по
на розв’язок задачі споживання. Для
цього продиференцюємо (1) по
 ,
тоді одержимо
,
тоді одержимо
 (2)
(2)
де
 і
і
 відображають ступінь чутливості стосовно
зміни
відображають ступінь чутливості стосовно
зміни
 .
.
Позначимо
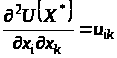 ,
тоді в матричному позначенні рівняння
(2) матимуть такий вигляд:
,
тоді в матричному позначенні рівняння
(2) матимуть такий вигляд:
 ,
,
де матриця коефіцієнтів є матрицею Гессе, що облямована цінами, тобто
 ,
де
,
де
 – вектор-рядок.
– вектор-рядок.
Припустимо, що
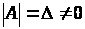 .
Розв’язок (2) знайдемо за методом Крамера.
При фіксованому значенні
.
Розв’язок (2) знайдемо за методом Крамера.
При фіксованому значенні
 одержимо
одержимо

де
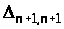 – алгебраїчні доповнення елементів
– алгебраїчні доповнення елементів
 ,
,
 відповідно.
відповідно.
Якщо
 ,
то
,
то
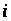 -й
товар називається коштовним
(цінним), при
збільшенні доходу попит на цей товар
також збільшується. На випадок, коли
-й
товар називається коштовним
(цінним), при
збільшенні доходу попит на цей товар
також збільшується. На випадок, коли

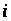 -й
товар називається малоцінним.
-й
товар називається малоцінним.
2.
Розглянемо вплив зміни ціни одного
товару, наприклад
 ,
на поведінку споживача. Диференціюючи
(1) по
,
на поведінку споживача. Диференціюючи
(1) по
 ,
одержимо:
,
одержимо:
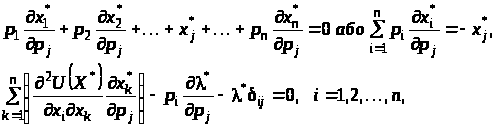 (3)
(3)
де
 – дельта Кронекера
– дельта Кронекера
 .
Запишемо систему (3) у такому вигляді:
.
Запишемо систему (3) у такому вигляді:
 .
.
Якщо матриця коефіцієнтів
невироджена, тобто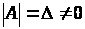 ,
тоді маємо при фіксованому
,
тоді маємо при фіксованому
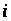 такий розв’язок, який називають рівнянням
Слуцького
такий розв’язок, який називають рівнянням
Слуцького

 (4)
(4)
Рівняння (4) є основним
рівнянням у теорії цінності. Вираз
 називається коефіцієнтом
Слуцького. З
рівняння Слуцького випливає, що при
змінюванні ціни на
називається коефіцієнтом
Слуцького. З
рівняння Слуцького випливає, що при
змінюванні ціни на
 -й
товар зміна попиту на
-й
товар зміна попиту на
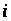 -й
товар наведена двома доданками, перший
одержав назву ефекту
заміни, другий
– ефекту
доходу. Отже:
« Загальний
ефект = вплив заміни + вплив доходу».
Наприклад, при зниженні ціни на
-й
товар наведена двома доданками, перший
одержав назву ефекту
заміни, другий
– ефекту
доходу. Отже:
« Загальний
ефект = вплив заміни + вплив доходу».
Наприклад, при зниженні ціни на
 -й
товар відбувається зростання доходу
(ефект доходу), але він іде не повністю
на закупівлю
-й
товар відбувається зростання доходу
(ефект доходу), але він іде не повністю
на закупівлю
 -го
товару – частина його витрачається на
закупівлю інших товарів (ефект заміни).
-го
товару – частина його витрачається на
закупівлю інших товарів (ефект заміни).
Нехай розв’язок (4)
справедливий для всіх
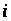 та
та
 таких, що
таких, що
 ,
тоді матриця
,
тоді матриця
 розміром
розміром
 симетрична й від’ємно
визначена, тобто
симетрична й від’ємно
визначена, тобто
 .
.
Можна встановити властивості цієї матриці.
Діагональні елементи виражають
чистий ефект заміщення, тобто визначають
зміну
 ,
яка є результатом варіації ціни
,
яка є результатом варіації ціни
 ,
за умови, що доход підтримується на
такому рівні, що значення
,
за умови, що доход підтримується на
такому рівні, що значення
 залишається незмінним.
залишається незмінним.
При
 товари
товари
 та
та
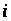 прийнято вважати взаємозамінюючими,
при
прийнято вважати взаємозамінюючими,
при
 – взаємодоповнюючими, а при
– взаємодоповнюючими, а при
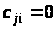 – незалежними.
– незалежними.
3 Коефіцієнт еластичності
Коефіцієнтом еластичності
функції одного аргументу
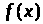 називається величина, отримана в
результаті ділення відносного приросту
функції на відносний приріст аргументу.
Позначаючи еластичність через
називається величина, отримана в
результаті ділення відносного приросту
функції на відносний приріст аргументу.
Позначаючи еластичність через
 ,
маємо за означенням
,
маємо за означенням
 ,
,
де
 – приріст аргументу;
– приріст аргументу;
 – викликаний ним
приріст функції.
– викликаний ним
приріст функції.
Звичайно праву частину помножують і ділять на 100% та говорять, що коефіцієнт еластичності показує, на скільки відсотків змінюється значення функції при зміні аргументу на 1%.
При
 маємо
маємо
 .
.
Якщо функція
 є функцією декількох аргументів, то
говорять про часткові коефіцієнти
еластичності
є функцією декількох аргументів, то
говорять про часткові коефіцієнти
еластичності
 .
.
Функція попиту
 є векторною функцією, її можна розглядати
як сукупність
є векторною функцією, її можна розглядати
як сукупність
 функцій попиту на окремі товари
функцій попиту на окремі товари
 ,
кожна з яких є функцією від
,
кожна з яких є функцією від
 змінної. Отже, для кожної з цих функцій
існує
змінної. Отже, для кожної з цих функцій
існує
 частковий коефіцієнт еластичності.
частковий коефіцієнт еластичності.
Залежно від типу аргументу розрізняють коефіцієнти еластичності за цінами й доходом.
Величини
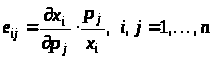 ,
що показують, на скільки відсотків
зміниться попит на
,
що показують, на скільки відсотків
зміниться попит на
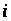 -й
товар у розрахунку зміни ціни
-й
товар у розрахунку зміни ціни
 -го
товару на 1%, називають коефіцієнтами
еластичності за цінами (якщо
-го
товару на 1%, називають коефіцієнтами
еластичності за цінами (якщо
 – то перехресними коефіцієнтами).
– то перехресними коефіцієнтами).
Показники
 ,
що характеризують аналогічно зміну
попиту від доходу, називаються еластичністю
за доходом.
,
що характеризують аналогічно зміну
попиту від доходу, називаються еластичністю
за доходом.
4 Алгоритми розв’язання задачі споживання
Умови Куна-Такера дають повну характеристику розв’язку, однак не містять конструктивного методу його пошуку. Одними з алгоритмів розв’язання задачі нелінійного програмування (ЗНП) є градієнтні методи.
Процес знаходження
розв’язку ЗНП градієнтними методами
полягає в тому, що, починаючи з деякої
точки
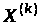 ,
здійснюється послідовний перехід до
деяких інших точок, поки не буде знайдений
прийнятний розв’язок задачі. При цьому
градієнтні методи розділяють на два
класи.
,
здійснюється послідовний перехід до
деяких інших точок, поки не буде знайдений
прийнятний розв’язок задачі. При цьому
градієнтні методи розділяють на два
класи.
До першого класу
відносять методи, в яких точки
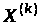 ,
що досліджуються, не виходять за межі
області припустимих розв’язків задачі.
Найпоширенішим з таких є метод
Франка-Вульфа.
,
що досліджуються, не виходять за межі
області припустимих розв’язків задачі.
Найпоширенішим з таких є метод
Франка-Вульфа.
До другого класу
методів відносять методи, під час
використання яких досліджувані точки
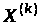 можуть як належати, так і не належати
області припустимих значень (метод
Ероу-Гурвіца, метод штрафних функцій).
можуть як належати, так і не належати
області припустимих значень (метод
Ероу-Гурвіца, метод штрафних функцій).
Під час знаходження
розв’язку задачі градієнтними методами
ітераційний процес здійснюється до
того моменту, поки градієнт функції в
черговій точці
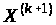 не стане дорівнювати нулю або ж поки
не стане дорівнювати нулю або ж поки
 ,
,
де
 – достатньо мале позитивне число, що
характеризує точність отриманого
розв’язку.
– достатньо мале позитивне число, що
характеризує точність отриманого
розв’язку.
Для чисельного розв’язування задачі споживача використовуватимемо метод Франка-Вульфа.
Нехай потрібно знайти
максимальне значення функції корисності
 за умови
за умови
 .
.
Характерною рисою даного методу є те, що обмеженням в задачі є лінійна нерівність. Ця особливість є основною для заміни нелінійної цільової функції лінійною поблизу досліджуваної точки, завдяки чому розв’язування задачі зводиться до послідовного розв’язання задач лінійного програмування.
Наприкінці першого розділу наведемо алгоритм методу Франка-Вульфа:
1. Процес знаходження розв’язку задачі починається з визначення точки, що належить області припустимих розв’язків задачі.
2. Знайдемо градієнт
цільової функції в точці

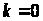
 .
.
3. Побудуємо лінійну
функцію

 .
.
4. Знайдемо максимум
 при обмеженні
при обмеженні
 ,
тобто розв’яжемо задачу лінійного
програмування (ЗЛП), звідки визначимо
вектор
,
тобто розв’яжемо задачу лінійного
програмування (ЗЛП), звідки визначимо
вектор
 ,
що доставляє максимум
,
що доставляє максимум
 .
.
5. Визначимо значення
оптимального кроку обчислення
 за формулою
за формулою
 .
.
6. Обчислимо компоненти нового припустимого розв’язку за формулою
 .
.
7. Знайдемо значення
 ,
,
 .
.
8. Порівняємо отримані
 ,
,
 з точністю
з точністю
 .
Якщо
.
Якщо
 ,
тоді
,
тоді
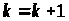 і алгоритм переходить до пункту 2, якщо
і алгоритм переходить до пункту 2, якщо
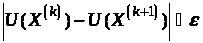 ,
тоді отримано оптимальний розв’язок
задачі
,
тоді отримано оптимальний розв’язок
задачі
 і
і
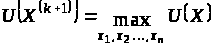 при
при
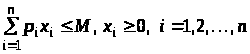 .
.