Анализ режимов автоматического управления

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН

СЕВЕРО-КАЗАХСТАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИРСИТЕТ ИМ. М. КОЗЫБАЕВА

Факультет энергетики и машиностроения

Кафедра энергетики и приборостроения

КУРСОВАЯ РАБОТА

"Анализ режимов автоматического управления "

Дисциплина: "Основы автоматики"

автор Вакульчик М.Ю

Преподаватель Кашевкин А.А.

Петропавловск 2011 г

Содержание

Введение

1. Исследование режимов системы автоматического управления

1.1 Определение передаточной функции замкнутой системы

1.2 Построение логарифмической амплитудной частотной характеристики

1.3 Построение логарифмической фазовой частотной характеристики

1.4 Временные характеристики САУ

1.5 Исследование устойчивости САУ

2. Синтез системы "объект-регулятор"

2.1 Расчет оптимальных параметров регуляторов

2.2 Выбор оптимального регулятора на основе экспериментальных исследований

Заключение

Список литературы

Введение

Автоматика - это область науки и техники, охватывающая теорию и принципы построения систем управления, действующих без непосредственного участия человека.

Первые автоматические устройства промышленного назначения были разработаны в связи с появлением паровых машин. Во второй половине 19 века появились автоматические устройства, основанные на использовании электрической энергии. Первоначально работы по созданию автоматических систем в механике, электротехнике, теплотехнике и других научных отраслях велись независимо друг от друга.

Для современной техники характерны значительное усложнение задач управления и рост объемов обрабатываемой информации, определяющие принципиальный качественный скачок автоматизации - широкое применение средств вычислительной техники.

Постоянное развитие науки и техники и интенсивное внедрение научно-технических достижений в производство обеспечивают непрерывное пополнение арсенала технических средств автоматики, вытесняя устаревшие элементы новыми, более современными конструкциями.

Основной задачей данной работы является ознакомление с основными методами построения систем автоматического управления и систем автоматического управления средствами, необходимыми для их реализации.

1. Исследование режимов системы автоматического управления

1.1 Определение передаточной функции замкнутой системы

Р
исунок 1. Функциональная схема системы регулирования температуры

ОР - объект регулирования;

РО - регулирующий орган;

Р - редуктор;

ДВ - двигатель;

УС - усилитель;

ЧЭ - чувствительный элемент;

U>ИЗ> - измеренное напряжение;

U - отклонение напряжения;

>1>> - >угол поворота вала двигателя;

>2> - угол поворота вала редуктора;

t>1> - температура на входе объекта;

t>2> - температура на выходе объекта;

U>З>> - >задающее напряжение;

U>1> - входное напряжение регулирования двигателя.

    Уравнение регулируемого объекта (1 + T>1>p) t>2> = k>1>t>1>p

где T>1 - >постоянная времени ОР; k>1> - коэффициент передачи.

автоматическое управление регулятор режим

2. Уравнение регулирующего органа t>1> = k>2>>2,>где k>2 - >коэффициент передачи;

3. Уравнение двигателя вместе с редуктором (1 + T>2>p) ∙p>2> = k>3>U>1>

где T>2 - >постоянная времени двигателя; k>3 - >коэффициент передачи;

4. Уравнение усилителя U>1> = k>4> ∙U

где k>4 - >коэффициент передачи;

5. Уравнение чувствительного элемента U>из> = k>5> ∙t>2>.

Передаточные функции:

    Усилитель (1.1)

    Двигатель и редуктор (1.2)

    Регулирующий орган (1.3)

    Объект регулирования (1.4)

    Чувствительный элемент (1.5)

1.2 Построение логарифмической амплитудной частотной характеристики

Определим тип исследуемого звена:

(апериодическое звено второго порядка)

Рассмотрим построение ЛАЧХ в случае апериодического звена второго порядка. Это звено не относится к числу элементарных звеньев, его можно представить как последовательное соединение двух апериодических звеньев первого порядка.

Для этого необходимо найти корни характеристического уравнения передаточной функции звена Т>3>, Т>4>.

(1.6)

Тогда передаточная функция апериодического звена второго порядка запишется следующим образом:

(1.7)

Уравнение асимптотической ЛАЧХ для апериодического звена второго порядка имеет вид

L (ω) ≈

Первая асимптота начинается в точке 20lgk и продолжается до точки сопрягающей частоты ω>1>=1/ T>3> - начало второй асимптоты, которая откладывается с наклоном - 20дБ/дек. Третья асимптота начинается в точке сопрягающей частоты ω>2>=1/ T>3> и имеет наклон уже - 40дБ/дек. В результате получим характеристику, изображенную на рис.2.

Рисунок 2. Амплитудная частотная характеристика апериодического звена второго порядка

1.3 Построение логарифмической фазовой частотной характеристики

Рассмотрим построение ЛФЧХ для апериодического звена второго порядка. Так как это звено можно представить в виде двух апериодических звеньев первого порядка, соединенных последовательно, то общая ЛФЧХ φ (ω) будет представлять собой сумму фазовых частотных характеристик апериодических звеньев первого порядка (рис.3).

φ (ω) = - arctg ωT>3 - >arctg ωT>4 (>1.9)

>>

ЛФЧХ в этом случае при ω→0 асимптотически стремится к оси частот, а при ω→∞ - к прямой φ= =-2π.

Рисунок 3. Логарифмическая фазовая частотная характеристика

1.4 Временные характеристики САУ

Важной характеристикой автоматических систем (звеньев) является переходные и импульсные переходные функции и их графики - временные характеристики.

Переходной функцией системы (звена) называют функцию, описывающую изменение выходной величины системы (звена), когда на ее вход подается единичное ступенчатое воздействие при нулевых начальных условиях. Другими словами, переходная функция h (t) есть функция, описывающая реакцию системы (звена) на единичное ступенчатое воздействие при нулевых начальных условиях.

При построении графика (рис.4) переходной функции апериодического звена второго порядка используется зависимость

(1.10)

где Т>3>> >и Т>4> корни характерестического уравнения передаточной функции (1.6).

Подставив заданные параметры колебательного звена k=19,35 Т>1>=0,0725, Т>2>=0,04, получим следующее выражение:

Рисунок 4. Переходная функция апериодического звена второго порядка

Импульсной переходной, или весовой, функцией системы (звена) называют функцию, описывающую реакцию системы (звена) на единичное импульсное воздействие при нулевых начальных условиях.

Весовая и переходная функции связаны между собой следующим образом:

ω (t) =h (t) ' (1.11)

Если исследуемое звено является апериодическим второго порядка, то импульсная характеристика (рис.5) будет соответствовать выражению:

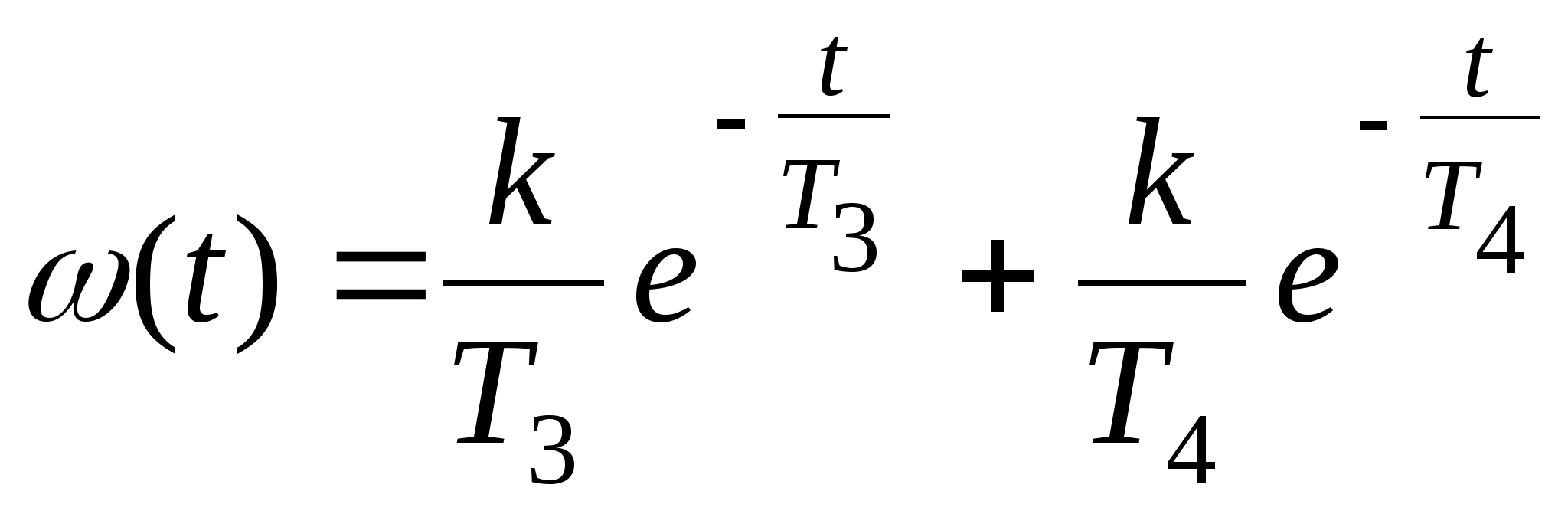(1.12)

Рисунок 5. Весовая характеристика апериодического звена второго порядка

1.5 Исследование устойчивости САУ

Устойчивость - это свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия.

Критерий устойчивости Рауса-Гурвица.

Это алгебраический критерий, по которому условия устойчивости сводятся к выполнению ряда неравенств, связывающих коэффициенты уравнения системы. В разной форме этот критерий был предложен английским математиком Е. Раусом и затем швейцарским математиком А. Гурвицем в конце прошлого века. Приведем без доказательства этот критерий в форме Гурвица.

Возьмем характеристический полином, определяющий левую часть уравнения системы,

D () = a>0>n + a>1>n - 1 + … + a>n>>-1> + a>n> (1.13)

где полагаем a>0> > 0, что всегда можно обеспечить умножением при необходимости полинома на - 1. Составим из коэффициентов этого полинома определитель

(1.14)

Этот определитель называется определителем Гурвица. Он имеет п строк и п столбцов. Первая строка содержит все нечетные коэффициенты до последнего, после чего строка заполняется до положенного числа п элементов нулями. Вторая строка включает все четные коэффициенты и тоже заканчивается нулями. Третья строка получается из первой, а четвертая - из второй сдвигом вправо на один элемент. На освободившееся при этом слева место ставится нуль. Аналогично сдвигом вправо на элемент получаются все последующие нечетные и четные строки из предыдущих одноименных строк.

Условие устойчивости заключается в требовании положительности определителя Гурвица и всех его диагональных миноров.

Развернем критерий Гурвица для нескольких конкретных значений п.

Для n =2

Условия устойчивости:

a>0> > 0; a>1> > 0; a>2> > 0

(к последнему неравенству сводится неравенство >2> > 0, если учесть предыдущее неравенство а>1> > 0).

Подставляя данные значения в уравнение имеем:

;

Можно сделать вывод, что система устойчивая.

2. Синтез системы "объект-регулятор"

2.1 Расчет оптимальных параметров регуляторов

Согласно заданию, передаточная функция объекта управления имеет вид:

(2.1)

К = 100;

Т>1> = 0,03;

Т>2> = 8.9;

Т>3> = 65;

Ψ = 0,92.

После подстановки числовых значений передаточная функция примет вид:

(2.2)

Далее, находится выражение инверсной расширенной амплитудно - фазовой характеристики объекта.

Согласно (2.3)

(2.4)

Так как заданное значение  = 0.92, то по формуле (2.5) определяется значение m (m = 0.402) и подставляем его в предыдущее выражение для расширенной амплитудно-фазовой характеристики.

; (2.5)

(2.6)

Из расширенной амплитудно-фазовой характеристики находятся действительная и мнимая части.

(2.7)

(2.8)

Перед тем, как определить оптимальные параметры настройки П, ПИ, ПИД регуляторов необходимо определить частоту среза объекта, которая находится из выражения для амплитудно-фазовой характеристики объекта управления. АФХ объекта получается после замены оператора р на jω в заданной передаточной функции объекта.

Таким образом, АФХ примет вид:

; (2.9)

По формуле (2.9), находится АЧХ объекта, на основании которой определяется частота среза.

(2.10)

АЧХ объекта управления имеет вид:

(2.11)

При нулевой частоте значение амплитуды равно 100. Следовательно, w=w>с>, откуда по формуле (2.12):

(2.12)

= 0.03*100 = 3.

Таким образом, необходимо решить уравнение:

(2.13)

Корни этого уравнения можно найти любым удобным методом, но при этом необходимо учитывать только положительные вещественные корни.

В данном случае для определения корней уравнения используется математический редактор Mathcad, результат расчета приведен на рисунке 6.

Рисунок 6. Результаты расчета корней уравнения в редакторе Mathcad.

Так как необходимо учитывать только положительные вещественные корни, то решением исходного уравнения являются следующий параметр w=w>c> = 0,45 с-1.

Для определения оптимальных параметров регулятора необходимо решить уравнение (2.14). Приравняв вещественные и мнимые части в уравнении (2.14) к соответствующим параметрам регулятора.

(2.14)

Расчет оптимальных параметров настройки для П - регулятора производится следующим образом:

(2.15)

Из второго уравнения системы определяется w любым удобным способом с учетом положительных вещественных корней и подставляется в первое уравнение системы. В данном случае w = 1,0218 с-1 и оптимальным параметром настройки П - регулятора является значение К>р>опт =0.972.

Для ПИ-регулятора расчет оптимальных значений параметров настройки производится следующим образом.

Для каждого значения частот от 0 до частоты среза определяются точки С>1>С>0> и С>1>, соответствующие требуемой степени затухания . Оптимальным параметром является точка на линии, равной степени затухания С>1>С>0> = f (С>1>), лежащая справа от глобального максимума.

Таким образом, для ПИ - регулятора по формуле (2.16) находятся параметры настройки:

(2.16)

(2.17)

Получаем уравнения:

,

Данные для построения графика зависимости С>1>С>0>=f (С>1>) для ПИ-регулятора приведены в таблице 1.

Таблица 1. Данные для определения параметров оптимальной настройки ПИ-регулятора.

w

C0

C1

C0*C1

0

0

-0,01

0

0,01

7,83E-05

-0,00449

-3,5E-07

0,02

0,00031

0,001107

3,43E-07

0,03

0,000691

0,00679

4,69E-06

0,04

0,001217

0,012558

1,53E-05

0,05

0,001884

0,018413

3,47E-05

0,07

0,003619

0,030378

0,00011

0,09

0,005862

0,042686

0,00025

0,1

0,007162

0,048967

0,000351

0,11

0,008575

0,055334

0,000475

0,12

0,010098

0,061785

0,000624

0,13

0,011724

0,068322

0,000801

0,14

0,013451

0,074942

0,001008

0,15

0,015272

0,081648

0,001247

0,16

0,017184

0,088437

0,00152

0,17

0,019183

0,095311

0,001828

0,18

0,021262

0,102269

0,002174

0, 19

0,023419

0,109311

0,00256

0,2

0,025648

0,116436

0,002986

0,21

0,027944

0,123645

0,003455

0,24

0,035194

0,145773

0,00513

0,26

0,040282

0,160941

0,006483

0,28

0,045529

0,17644

0,008033

0,3

0,050899

0, 192269

0,009786

0,32

0,056355

0, 208427

0,011746

0,34

0,061858

0,224913

0,013913

0,36

0,067372

0,241726

0,016286

0,38

0,072858

0,258865

0,01886

0,4

0,078279

0,276328

0,021631

График зависимости С>1>С>0>=f (С>1>) для ПИ-регулятора приведен на рисунке 7.

Рисунок 7. График зависимости С>1>С>0 >= f (C>1>) для ПИ - регулятора

Максимальное значение функции С>1>С>0> = 0.07858 при С>1> = 0.6919. Необходимо выбрать точку правее глобального максимума. Следовательно можно взять С>1> = 0.7525, С>1>С>0> = 0.748. В результате решения системы уравнений определяются оптимальные параметры настройки

,

Оптимальные параметры настройки для ПИД - регулятора в соответствии с формулой (2.18)

(2.18)

с учетом того, что α=0,1, определяются следующим образом:

Данные для построения графика зависимости С>1>С>0>=f (С>1>) для ПИД-регулятора приведены в таблице 2.

Таблица 2. Данные для определения параметров оптимальной настройки ПИД-регулятора

w

C0

C1

C0*C1

0,01

0,003201

0,246648

0,00079

0,02

0,00648

0,249266

0,001615

0,03

0,009833

0,252096

0,002479

0,04

0,013258

0,255131

0,003382

0,05

0,016753

0,258366

0,004328

0,06

0,020317

0,261794

0,005319

0,07

0,023946

0,265412

0,006355

0,08

0,027638

0,269213

0,00744

0,09

0,031392

0,273194

0,008576

0,1

0,035204

0,277351

0,009764

0,12

0,042997

0,286175

0,012305

0,14

0,050998

0,295658

0,015078

0,16

0,059189

0,305773

0,018099

0,18

0,067553

0,3165

0,021381

0,2

0,076071

0,327819

0,024937

0,22

0,084723

0,339711

0,028782

0,24

0,093493

0,352162

0,032925

0,26

0,102362

0,365158

0,037378

0,28

0,11131

0,378686

0,042152

0,3

0,12032

0,392735

0,047254

0,32

0,129373

0,407295

0,052693

0,34

0,138449

0,422358

0,058475

0,36

0,147531

0,437916

0,064606

0,38

0,156599

0,453962

0,07109

0,4

0,165634

0,470491

0,077929

0,42

0,174618

0,487497

0,085126

0,45

0,187954

0,513891

0,096588

0,5

0, 209653

0,560216

0,117451

0,55

0,23043

0,609431

0,140431

0,6

0,249981

0,661528

0,165369

0,7

0,284179

0,774475

0,220089

0,8

0,309771

0,89959

0,278667

0,9

0,324242

1,038137

0,336607

1

0,325035

1, 192686

0,387665

1,2

0,275177

1,578054

0,434245

1,4

0,138978

2,34694

0,326173

1,5

0,0317

5,506128

0,174544

1,8

-0,48041

1,932086

-0,9282

2

-1,00911

2,457965

-2,48036

График зависимости С>1>С>0>=f (С>1>) для ПИД-регулятора приведен на рисунке 8

Рисунок 8. График зависимости С>1>С>0 >= f (C>1>) для ПИД - регулятора

Максимальное значение функции С>1>С>0> = 0.4342 при С>1> = 1.578. Необходимо выбрать точку правее глобального максимума. Следовательно можно взять С>1> = 2.346, С>1>С>0> = 0.326. В результате решения системы уравнений определяются оптимальные параметры настройки:

,

,

.

2.2 Выбор оптимального регулятора на основе экспериментальных исследований

В соответствии с заданием курсовой работы необходимо выполнить проверку рассчитанных параметров регуляторов в программах электронного моделирования. С помощью пакета Simulink программы MATLAB строится модель исследуемой системы с различными типами регуляторов и по виду переходной характеристики выбирается оптимальный регулятор.

Модель исследуемой системы без регуляторов (рис.9).

Рисунок 9. Модель системы без регулятора

Переходная система характеристики исследуемой модели приведена на рисунке 10.

Рисунок 10. Переходная характеристика системы

Модель исследуемой системы с П-регулятором приведена на рисунке 11.

Рисунок 11 - Модель системы с П - регулятором

Переходная характеристика системы с П-регулятором приведена на рисунке 12.

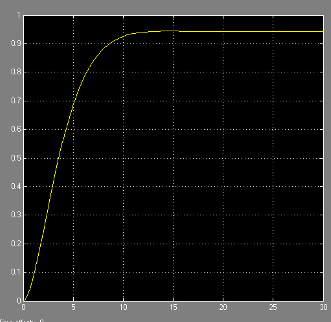
Рисунок 12. Переходная характеристика с П-регулятором

ПИ-регулятор можно представить как параллельное соединение пропорционального и интегрирующего звеньев. Коэффициент передачи пропорционального звена в соответствии с расчетом, приведенным выше, равен 0,752, коэффициент передачи интегрирующего звена равен . Таким образом, модель исследуемой системы с ПИ-регулятором приведена на рисунке 13.

Рисунок 13. Модель системы с ПИ-регулятором

Переходная характеристика системы с ПИ-регулятором приведена на рисунке 14.

Рисунок 14. Переходная характеристика системы с ПИ-регулятором

ПИД-регулятор можно представить как параллельное соединение пропорционального, интегрирующего и дифференцирующего звеньев. Коэффициент передачи пропорционального звена в соответствии с расчетом, приведенным выше, равен 2.346, коэффициент передачи интегрирующего звена равен , коэффициент передачи дифференцирующего звена равен . Таким образом, модель исследуемой системы с ПИД-регулятором приведена на рисунке 15.

Рисунок 15. Модель системы с ПИД-регулятором

Переходная характеристика системы с ПИД-регулятором приведена на рисунке 16.

Рисунок 16. Переходная характеристика системы с ПИД-регулятором

Заключение

В ходе выполнения данной работы, исследования режимов автоматического управления построены: временные, логарифмические и фазовые характеристики.

Определены оптимальные параметры настройки П, ПИ, ПИД-регуляторов. На основании полученных характеристик можно сделать вывод, что для заданного объекта управления оптимальным является ПИД-регулятор (перерегулирование составляет менее 15%). При использовании П-регулятора наблюдается статическая ошибка, а при ПИ-регуляторе наблюдается расходящийся колебательный процесс.

Список литературы

    Теория автоматического управления / Под ред. А.А. Воронова. - М.: ВШ, 1986г.

    Г.А. Атамалян Приборы и методы измерения электрических величин. - М.: Дрофа, 2005г.

    В.Ю. Шишмарев Автоматика. - М. ACADEMIA, 2005г.

    Никулин В.А. Частотные методы анализа и синтеза теории автоматического управления. - 2-е изд., испр. и доп. - М.: Наука, 2000.

    Лукас В.А. Теория автоматического управления. - 2 изд., перераб. и доп. - М.: Недра, 1990.

    Баскаков С.И. Радиотехнические цепи и сигналы: Учеб. для вузов по спец. "Радиотехника". - 4-е изд., перераб. и доп. - М.: Высш. шк., 2003.

    Шавров А.В., Коломнец А.П. Автоматика. - М.: Колос, 1999.

    Загинайлов В.И., Шеповалова Л.Н. Основы автоматики. - М.: Колос, 2001