Цепи переменного электрического тока
ЗАДАЧИ
ПО ТЕМЕ ЦЕПИ ПеременнОГО ЭЛЕКТРИЧЕСКОГО ТОКА
Задача № 2.1
Имеется цепь переменного тока частотой f = 50 Гц с активно-индуктивной нагрузкой (рис. 1). Показания приборов (амперметра, вольтметра, ваттметра) приведены в таблице 1.

Рис. 1. Схема к задаче 2.1
С учетом приведенных данных требуется определить (рассчитать):
параметры резистора r>1> и индуктивности L>1> катушки;
величины напряжений на резисторах и на участке bd;
углы сдвига фаз между напряжением и током на входе цепи и на участке bd;
параметры схемы для построения векторной диаграммы.
Таблица 1. Задание к задаче № 2.1
|
I, А |
8,1 |
|
U, В |
220 |
|
P, Вт |
700 |
|
r>2>, Ом |
6 |
Решение
1. На рис. 1 приведена электрическая схема.
2. Определение различных параметров.
3. Значение cos с учетом показания приборов:
P = UI
cos;

 .
.
4. Значение угла ,
град:
 град.
град.
5. Значение угла ,
град:
 рад.
рад.
6. Общее активное сопротивление R, учитывая, что ваттметр показывает активную мощность
Р: P = I 2(r>1> + r>2>) = I 2R;
 Ом.
Ом.
7. Сопротивление
r>1: >R = r>1> + r>2:>
 Ом.
Ом.
8. Модуль Z полного комплексного сопротивления:
Z = U/I;
Z = 220:8,1 = 27,16 Ом.
9. Индуктивное сопротивление
X>L>: Z2 = R2 + X>L>2;
 Ом.
Ом.
10. Величина индуктивности
L: X>L> = 2fL;
 Гн.
Гн.
11. Модуль полного сопротивления участка bd:
Z>bd> = (r>1>2 + X>L>2)0,5;
 Ом.
Ом.
12. Модуль комплексного напряжения Ů>1 >на резисторе R>1>:
U>1 >=IR>1>;
U>1 >= В.
В.
13. Модуль комплексного напряжения Ů>2> на резисторе R>2>:
U>2>=IR>2> ;
U>2 >= В.
В.
14. Модуль комплексного напряжения Ů>L>> >на индуктивности сопротивлением X>L>:
U>L>> >= IX>L>;
U>L>
= В
В
15. Проверить правильность расчета напряжений, сравнив модуль суммарного расчетного напряжения U>расч> с заданным U:
U>расч >= [(U>1 >+U>2>)2 + U>L>2]0,5;
U>расч
>= В.
В.
16. Модуль комплексного напряжения U>bd> на участке bd:
U>bd> = IZ>bd>;
U>bd>
= В.
В.
17. Сдвиг фаз
= >1>: >1 >= arctg(X>L>/r>1>);
>1 >= град.
град.
18. Сдвиг фаз
= >1>
в радианах: >1
>= рад.
рад.
19. Построение векторной диаграммы токов и напряжений цепи.
Векторная диаграмма строится по следующим этапам:
выбираем масштабы для векторов напряжения и тока (рис. б, в), например, 1см - 1 А; 0,5 см - 100 В;
рисуем оси +1 и +j (ось +j направляем, например, вверх);
на комплексной плоскости отмечаем точку, от которой будем строить вектора напряжений и токов (этой точке соответствует точка а схемы);
поскольку в задаче не дается начальный угол вектора тока İ, по умолчанию, принимаем его равным нулю, поэтому вектор İ направлен по оси +1;
поскольку сдвига фаз между током и напряжением на резисторах нет, то вектора Ů>1>, Ů>2> направлены по оси +1;
поскольку вектор напряжения Ů>L>> >опережает ток İ на 90 о (идеальная индуктивность), то направляем вектор Ů>L> по оси +j;
геометрическая сумма векторов Ů>1>, Ů>2> направлена по оси +1; геометрическая сумма векторов Ů>1>, Ů>2>, Ů>L> дает суммарный вектор Ů; после построения с помощью транспортира, проверяем, равен ли угол >геом>, расчетному значению
вектор Ů>bd> находим, с учетом того, что он направлен из конца вектора Ů>2 >в конец вектора Ů.

Рис. 2. Векторная диаграмма
Задача № 2.2
К генератору переменного тока с фиксированным напряжением U подключена цепь, состоящая из последовательно соединенных катушки c активным сопротивлением R и индуктивностью L, а также конденсатора с емкостью С.
Параметры цепи приведены в таблице 2.2. Частота генератора = 2f может изменяться в широких пределах, так что при частоте f>0> наступает режим резонанса напряжения.
При изменении частоты питающего генератора в пределах 0 < f>0> < 2f>0> рассчитать и построить:
частотные характеристики элементов цепи R(f), X>L>(f), X>C>(f) и всей цепи в целом Z(f);
зависимости I(f), U>R>(f), U>L>(f), U>C>(С), представив их анализ от рода нагрузки;
фaзочастотную характеристику – зависимость сдвига фаз между напряжением U на клеммах генератора и током I в цепи от частоты f генератора;
рассчитать коэффициент усиления напряжения К, добротность волновое сопротивление цепи ;
параметры схемы для построения векторной диаграммы.

Рис. 3. Схема к задаче № 2.2
Таблица 2. Задание к задаче № 2.2
|
U, B |
70 |
|
R, Ом |
8 |
|
L, мГн |
60 |
|
С, мкФ |
60 |
Решение
1. Схема представлена на рис. 3.
2. Задание к задаче приведено в таблице 2.
3. Определить (рассчитать) значения всех параметров в системе СИ.
4. Оценить, какой резонанс наблюдается в исследуемой цепи? Резонанс напряжений.
5. Значение частоты f>0 >резонанса напряжений:
X>C>>0 >= 1/>0>C = Х>L>>0 >= >0>L; f>0 >= >0>/2=1/2CL)0,5;

f>0 >=
 =
83,93 Гц.
=
83,93 Гц.
6. Значение реактивного индуктивного сопротивления Х>L>>0>(f>0>) при резонансе:
Х>L>>0> = >0>L;
Х>L>>0>(f>0>)
= =
31,62 Ом.
=
31,62 Ом.
7. Значение реактивного емкостного сопротивления Х>С0>(f>0>) при резонансе:
X>C>>0 >= 1/>0>C;
Х>С0>(f>0>)= = 31,62 Ом.
= 31,62 Ом.
8. Модуль полного комплексного сопротивления цепи при резонансе:
Z(f>0>) = [R2 +(Х>L>>0> X>C>>0>)2]0,5;
Z(f>0>)
= =
8 Ом.
=
8 Ом.
9. Модуль тока İ при резонансе:
I(f>0>) = U/Z(f>0>);
I(f>0>)
= =
8,75 А.
=
8,75 А.
10. Модуль напряжения на индуктивности в режиме резонанса:
U>L>(f>0>) = I(f>0>)X>L>(f>0>)%;
U>L>(f>0>)
= =
276,68 В.
=
276,68 В.
11. Модуль напряжения на конденсаторе:
U>С>(f>0>) = I(f>0>)X>С>(f>0>);
U>С>(f>0>)
= =
276,68 В.
=
276,68 В.
12. Коэффициент усиления напряжения К:
К = U>L>/U = U>С>/U;
К = =
3,95.
=
3,95.
13. Величина добротности:
= /R = X>L>/R = X>L>I>рез>/RI>рез>= К;
= 3,95.
14. Построить (табличным способом или в программе Excel) частотные характеристики элементов цепи R(f), X>L>(f), X>C>(f) и всей цепи в целом Z(f) в диапазоне частот 0 < f < 2f>0 >(рис. 4, а).
15. Построить зависимости I(f), U>R>(f), U>L>(f), U>C>(С) и провести их анализ в различных диапазонах частот (рис. 4, б)
16. Построить фaзочастотную характеристику – зависимость сдвига фаз между напряжением U на клеммах генератора и током I в цепи от частоты f генератора: f) = arctg[(X>L>> >− X>C>)/R] (рис. 4, в)
а)

б)
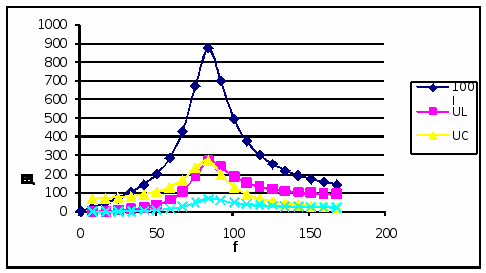
в)

Рис. 4. Характеристики к задаче 2.2.
Задача № 2.6
Цепь, представленная на рис. 2.6, а, находится в режиме резонанса тока. На входе цепи действует переменное напряжение u(t), оригинал которого равен u(t) = U>m>sin(t + >U>). При этом мгновенный ток i(t) в цепи изменяется по закону: i(t) = i>m>sin(t + >I>). Параметры цепи приведены в таблице 6.

Рис. 6. Схема к задаче № 2.6
Таблица 3. Задание к задаче № 2.6
|
i>m>, A |
13 |
|
>I> , град |
17 |
|
R, Ом |
7 |
|
X>L>, Ом |
4 |
|
>0>, рад/с |
104 |
С учетом параметров цепи требуется определить:
значение емкости конденсатора С;
выражения для оригиналов токов i>1(>t), i>2(>t), u(t);
мощности, потребляемые цепью в режиме резонанса;
параметры схемы для построения векторной диаграммы токов цепи при резонансе.
Для электрической схемы, соответствующей номеру варианта, выполнить этапы следующие расчета.
1. Зарисовать схему и записать задание, соответствующее номеру варианта (рис. 6, табл. 6).
2. Определить (рассчитать) параметры схемы.
3. Оригинал тока i(t), в соответствии с заданием варианта:
i(t) = 13sin(104t + 17о) А.
4. Выражение для комплекса действующего значения тока İ (комплексного тока), соответствующего оригиналу в алгебраической и показательной формах: İ = (13/2)e j17 = 9,286 e j17 = 8,88 + j2,71A
5. Поскольку в цепи выполняется режим резонанса токов, учесть, что условие резонанса токов характеризуется равенством модулей реактивных проводимостей параллельных ветвей ImY>bce> = ImY>bde>. Для этого рассчитываются следующие величины.:
6. Комплексное сопротивление Z>1 >ветви bce:
Z>1>= R+ jL; Z>1>= 7 + j4 = 8,05e j29,74Ом.
7. Комплексная проводимость Y>1 >ветви bce:
Y>1 >= 1/ Z>1>; Y>1>=0,124e j29,74= 0,108 j0,0615 Cм.
8. Модуль реактивной Y>2 >комплексной проводимости ветви bde:
ImY>2> = ImY>3>; ImY>2> = 0,0615 См.
9. Величина емкости С:
ImY>2> = 1/X>C>> >= >0>C; C = 6,15 мкФ.
10. Комплексное сопротивление Z>2 >ветви bde:
Z>2>= 0 jX>C> = j/>>C; Z>2 >= 16,26e j90 = 0 j16,26 Ом.
11. Комплексная проводимость Y>2 >ветви bde:
Y>2 >= 1/Z>2>; Y>2>= 0,0615е j90 = 0 + j0,0615 Ом.
12. Полная комплексная проводимость Y цепи ae:
Y = Y>1 >+ Y>2>; Y = 0,108е j0 = 0,108 + j0 Cм.
13. Комплексное напряжение Ů (комплекс действующего напряжения):
Ů = İ/Y = 85,98е j17 = 82,22 + j25,14 B.
14. Комплекс напряжения Ů>m> (комплексная амплитуда):
Ů>m> = Ů2; Ů = 120,37е j17= 115,11 + j35,19 B.
15. Оригинал u(t):
u(t) = 120,37sin(104t + 17о) B.
16. Комплексный ток İ>1>:
İ>1 >= Ů/Z>1>; İ>1 >= 14,95е j-12,74 = 14,58 – j3,3 А.
17. Комплекс İ>1>>m>:
İ>1>>m>> >= İ>1>2; İ>1>>m>> >= 20,93е j-12,74A.
18. Оригинал i>1>(t):
i>1>(t) = 20,93sin(104t -12,74о) A.
19. Комплексный ток İ>2>:
İ>2 >= Ů/Z>2>; İ>2 >= 5,29е j107 = 1,55 + j5,06 А.
20. Комплекс İ>2>>m>:
İ>2>>m>= İ>2>2; İ>2>>m>> >= 7,406е j107 A.
21. Оригинал i>2>(t):
i>2>(t) = 7,406sin(104t + 107о) A.
22. Активная мощность при резонансе c учетом = 0:
P = UIcos; P = 85,98*8,88 = 763,5 Вт.
23. Реактивная мощность при резонансе c учетом = 0:
Q = UIsin; Q = 0 вар.
24. Полная мощность при резонансе:
S = (P2 + Q2)0,5; S = 763,5 ВА.
25. Рисуем векторные диаграммы токов и напряжений для цепи при резонансе (рис. 7).

Рис. 7. Векторная диаграмма токов и напряжений
Задача № 2.10
Параметры схемы четырех проводной цепи переменного тока, представленной на рис. 8, приведены таблице 4. Приемники соединены звездой с нейтральным проводом (генератор не указан). Заданы: линейное напряжение U>л>, активные r>i>, реактивные x>iL> или x>iC> (индекс L – индуктивное, индекс С - емкостное) сопротивления фаз a, b, c приемника.
Таблица 4. Задание к задаче № 2.10
|
U>л>, В |
127 |
|
r>a, >Ом |
30 |
|
r>b, >Ом |
10 |
|
r>c, >Ом |
24 |
|
x>aL>, Ом |
10 |
|
x>bL>, Ом |
2 |
|
x>cC>, Ом |
28 |
Необходимо рассчитать параметры приведенной сети для различных режимов:
режим 1: четырех проводная сеть (с нейтральным проводом);
режим 2: обрыв провода фазы А при наличии нейтрального провода;
режим 3: короткое замыкание фазы В и обрыв нейтрального провода.
Для всех перечисленных режимов необходимо нарисовать схему, в соответствии с исследуемым режимом, а также рассчитать:
комплексы фазных токов и напряжений;
комплексные сопротивления;
мощность трехфазной системы;
построить векторные диаграммы фазных токов и напряжений;

Рис. 8. Схема к задаче № 2.10 (соединение звездой с нейтральным проводом)
Для электрической схемы, соответствующей номеру варианта, выполнить следующие этапы расчета.
1. Зарисовать схему и записать задание, соответствующее номеру варианта (рис. 8, табл. 4).
2. В соответствии со схемой предполагается наличие несимметричной нагрузки. Поэтому весь расчет производить для каждой из фаз, например. Условно принимаем, что вектор Ů>а> направлен по оси действительных величин , т.е. полагается, что начальная фаза фазного напряжения Ů>а> равна нулю.
3. Определить (рассчитать) параметры цепи.
4. Режим 1. Четырех проводная сеть (с нейтральным проводом) (рис. 8)
5. Задаемся нулевой фазой для фазного напряжения Ů>а>; >a>> >= 0 град.
6. Комплекс действующего фазного напряжения Ů>а> (пренебрегаем падением напряжения на линии):
Ů>a> = Ė>A>> >= U>a>e jа; Ů>a>> >= Ė>A>> >= 73,41e j0 = 73,41+ j0 B.
7. Комплекс действующего фазного напряжения Ů>b> (пренебрегаем падением напряжения на линии):
Ů>b>> >= Ė>B> = U>b>ej120; Ů>b>> >= Ė>B> = 73,41ej120 = 36,7 j63,57 B.
8. Комплекс действующего фазного напряжения Ů>c>> >(пренебрегаем падением напряжения на линии):
Ů>c>> >= Ė>C> = U>c>e+j120; Ů>c>> >= Ė>C> = 73,41e+j120 = −36,7 + j63,57 B.
9. Комплекс действующего линейного напряжения Ů>а>>b> на приемнике:
Ů>ab> = Ů>ab> = Ů>a> Ů>b>; Ů>ab>> >= 127e+j30 = 109,99 + j63,5 B.
10. Комплекс действующего линейного напряжения Ů>bc> на приемнике:
Ů>bc> = Ů>bc> = Ů>b> Ů>c>; Ů>bc>> >= 127ej90 = 0 j127 B.
11. Комплекс действующего линейного напряжения Ů>ca> на приемнике:
Ů>ca> = Ů>ca> = Ů>c> Ů>a>; Ů>ca>> >= 127e j150 = -109,99 + j63,57
12. Комплексное сопротивление нагрузки Z>a> фазы А:
Z>a>> >= 30 + j10 = 31,58e+j18,43 Ом.
13. Комплексное сопротивление нагрузки Z>b> фазы В:
Z>b>> >= 10 + j2 = 10,2e+j11,31 Ом.
14. Комплексное сопротивление нагрузки Z>c> фазы С:
Z>c>> >= 24 j28 = 36,92ej49 Ом.
15. Комплексный ток İ>a>:
İ>a >= Ů>a>/Z>a>; İ>a >= 2,2- j0,73 = 2,32e j-18,43 A.
16. Комплексный ток İ>b>:
İ>b >= Ů>b>/Z>b>; İ>b >=4,75 − j5,4 = 7,2ej131,31 A.
17. Комплексный ток İ>c>:
İ>c >= Ů>c >/Z>c>; İ>c >= 1,81 − j0,35 = 1,84e j169 A.
18. Комплексный ток в нейтральном проводе:
İ>N>> >= İ>a>> >+ İ>b> + İ>c> ; İ>N>> >= 4,36 − j6,48 = 7,79ej56,07 A.
19. C учетом полученных данных строится векторная диаграмма токов и напряжений (рис. 9).

Рис. 9. Векторная диаграмма токов и напряжений
20. Определение мощностей системы (с нейтральным проводом)
21. Полная, активная, реактивная мощности фазы а:
S>a>> >= Ů>a>I>a>*;
S>a>> >= 170,31e j-18,43 = 161,57 - j53,84 ВА;
Р>а >= 161,57 Вт;
Q>a>> >= -53,84 вар.
22. Полная, активная, реактивная мощности фазы b:
S>b>> >= Ů>b>I>b>*;
S>b>> >= 528,55e j-251.31 = -169,37 + j500,68 ВА;
Р>b>> >= -169,37 Вт;
Q>b>> >= 500,68 вар.
23. Полная, активная, реактивная мощности фазы c:
S>c>> >= Ů>c>I>c>*;
S>c>= 135,07ej189 = -133,4 j21,13 ВА;
Р>с >= -133,4 Вт;
Q>с >= −21,13 вар.
24. Полная, активная, реактивная мощности на нагрузке трех фаз:
S = S>a >+ S>b >+ S>c>;
S = -141,2 + j 425,71 ВА;
Р = -141,2 Вт;
Q = 425,71 вАр.
25. Режим 2. Обрыв провода фазы А при наличии нейтрального провода (рис. 10).

Рис. 10. Схема к задаче № 2.10 (соединение звездой с обрывом фазы А с нейтральным проводом)
В случае наличия нейтрального провода векторы всех фазных токов и напряжений, как и в случае 1, имеют общее начало в т. N = n (рис. 10), поэтому Ů>nN> = Ė>В>. При этом: фазные напряжения Ů>a>, Ů>b>, Ů>c>, рассчитанные в пп. 5-8 не изменяются; ток в фазе а – отсутствует. Следовательно: İ>а >= 0; токи İ>b>, İ>с >в фазах b и с – не изменяются.
26. Комплексный суммарный ток в нейтральном проводе:
İ>N>> >= İ>a>> >+ İ>b> + İ>c>; İ>N>> >= 6,56 − j7,21 = 9,79 ej47,7 A.
27. C учетом полученных данных строится векторная диаграмма токов и напряжений (рис. 11).

Рис. 11 Векторная диаграмма токов и напряжений
28. Полная, активная, реактивная мощности фазы а:
S>a>> >= Ů>a>I>a>*;
S>a>> >= 0e j0 = 0 + j0 ВА; Р>а >= 0 Вт; Q>a>> >= 0 вар.
29. Полная, активная, реактивная мощности фазы b;
S>b>> >= Ů>b>> >I>b>*;
S>b>> >= 528,55e j-251.31 = -169,37 + j500,68 ВА;
Р>b>> >= -169,37 Вт;
Q>b>> >= 500,68 вар.
30. Полная, активная, реактивная мощности фазы c:
S>c>> >= Ů>c>I>c>*;
S>c>= 135,07ej189 = -133,4 j21,13 ВА;
Р>с >= -133,4 Вт;
Q>с >= −21,13 вар.
31. Полная, активная, реактивная мощности на нагрузке трех фаз:
S = S>a >+ S>b >+ S>c>;
S = -302,77 + j 478,87 ВА;
Р = -302,77 Вт;
Q = 478,87 вАр.
32. Режим 3. Короткое замыкание фазы В и обрыв нейтрального провода (рис. 12).

Рис. 12. Схема к задаче № 2.10 (соединение звездой с КЗ фазы В, обрыв нейтрали)
В данном режиме потенциалы точек n и b совпадают, поэтому на векторной диаграмме (рис. 14) нейтральная точка n сместится в точку b. При отсутствии нейтрального провода нагрузка фаз А и С оказывается включенными на линейное напряжение, т.е.
Ů>а >= Ů>ab>, Ů>b>> >= 0; Ů>c>> >= Ů>bc>.
Сумма токов в точке n равна 0; значения Ů>ab>, Ů>bc> рассчитаны в пп. 9, 10.
33. Комплексный ток İ>a> в фазе А:
İ>a >= Ů>а>/Z>a> = Ů>ab>/Z>a>; İ>a >= 4,02e j11,57 = 3,94+ j0,11 A.
34. Комплексный ток İ>c>> >в фазе C;
İ>c>> >= Ů>c>/Z>c>> >= Ů>bc>/Z>c>:
İ>c>> >= 3,44e -j101 = −0,66 – j3,38A.
35. Комплексный ток в İ>b>> >в проводе фазы В:
İ>b>> >= (İ>a> + İ>c>); İ>b>> >= -4,62ej44,9 = -3,28 + j3,27 A.54.
C учетом полученных данных строится векторная диаграмма токов и напряжений (рис. 13).
55. Полная, активная, реактивная мощности фазы а:
S>a >= Ů>ab>I>a>*;
S>a >= 510,51e j41,57 = 381,94 + j338,74 ВА;
Р>а >= 381,94 Вт;
Q>a>> >= 338,74 вар.
36. Полная, активная, реактивная мощности фазы c:
S>c>> >= −Ů>BC>I>c>*;
S>c>> >= 436,88ej49 = 286,62 j329,72 ВА;
Р>c>> >= 286,62 Вт;
Q>с >= 329,72 вар.
37. Полная, активная, реактивная мощности на нагрузке трех фаз:
S = S>a >+ S>c>; S = 668,56 + j9,02 ;
Р>1 >= 668,56 Вт;
Q>1 >= 9,02 вар.

Рис. 13 Векторная диаграмма токов и напряжений
Задача № 2.11
Параметры схемы трехфазной цепи переменного тока, представленной на рис. 14, приведены в таблице 5. Приемники соединены треугольником (генератор не указан). Заданы: напряжение U, активные r>i>, реактивные x>iL> или x>iC> (индекс L – индуктивное, индекс С - емкостное) сопротивления фаз ab, bc, cа приемника.
С учетом параметров цепи требуется определить:
комплексы действующих фазных напряжений;
комплексные сопротивления фаз приемника;
комплексные фазные и линейные токи;
потребляемую активную мощность, используя показания ваттметров;
параметры цепи для построения векторной диаграммы токов и напряжений.
Примечание: если в тексте не говорится, о каком напряжении U идет речь, то однозначно понимается, что имеется в виду линейное напряжение, т.е.
U = U>л>.
Таблица 5, Задание к задаче № 2.11
|
U>л>, В |
380 |
|
r>ab>>, >Ом |
6 |
|
r>bc, >Ом |
7 |
|
r>ca, >Ом |
5 |
|
x>abL>Ом |
3,2 |
|
x>bcL>,> >Ом |
2 |
|
x>caC>, Ом |
6 |

Рис. 14. Схема к задаче № 2.11
Для электрической схемы, соответствующей номеру варианта, выполнить следующие этапы расчета.
1. Зарисовать схему и записать задание, соответствующее номеру варианта (рис. 14; табл. 5).
2. В соответствии со схемой предполагается: при несимметричной нагрузке каждую фазу схемы можно рассматривать независимо от других фаз. Условно принимаем, что вектор Ů>b>>c> направлен по оси действительных величин (рис. 15), т.е. полагается, что начальная фаза фазного напряжения Ů>b>>с> равна нулю.
3. Определить (рассчитать) следующие параметры.
4. Комплекс действующего фазного напряжения
Ů>b>>с>: Ů>bс >= Ue j0.
5. Комплекс действующего фазного напряжения Ů>ab>:
Ů>ab>> >= 380e j120 = 190 + j329,09 B.
6. Комплекс действующего фазного напряжения Ů>ca>:
Ů>ca>> >= 380ej120 = 190 j329,09 B.
7. Комплексное сопротивление Z>ab> фазы приемника:
Z>ab> = r>ab>> >+ jx>ab>; Z>ab>= 6 + j3,2 = 6,82е j28,07 Ом.
8. Комплексное сопротивление Z>b>>с >фазы приемника:
Z>bc>> >= r>bc>> >+ jx>bc>; Z>bc>> >= 8 + j3 = 8,51е j20,56 Ом.
9. Комплексное сопротивление Z>ca> фазы приемника:
Z>ca>> >= r>ca>> >+ jx>ca>; Z>ca>= 6 j7 = 9,23еj49,4 Ом.
10. Комплексный фазный ток İ>ab>:
İ>ab>> >= Ů>ab>/Z>ab>; İ>ab>= 55,72e j91,33 = -1,88 + j55,7 A.
11. Комплексный фазный ток İ>bc>:
İ>bc>> >= Ů>b>>c>/Z>bc>; İ>bc> = 44,65e j0 = 44 ,65+ j0 A.
12. Комплексный фазный ток İ>ca>:
İ>ca>> >= Ů>ca>/Z>ca>; İ>ca>= 41,17ej70,6 = 13,68 j38,83 A.
13. Линейный ток İ>А> по первому закону Кирхгофа:
İ>А>> >= İ>ab > İ>ca>; İ>А>> >= 15,56 + j16,87 = -22,88e j-47,3 A.
14. Линейный ток İ>B> по первому закону Кирхгофа:
İ>B >= İ>bc > İ>ab>; İ>B >= 46,53 j55,7= 72,70ej50,13 A.
15. Линейный ток İ>C> по первому закону Кирхгофа:
İ>C >= İ>ca > İ>bc>; İ>C >= 30,97 j38,83 = 49,95еj51,42 A.
16. Комплекс мощности S>1>:
S>1 >= Ů>AB> I*>А>; S>1 >= 8694,4e j72,7 =2585,5 + j8301,07 ВА.
17. Показание ваттметра W>1> – активная мощность Р>1>:
Р>1 >= ReS>1>;Р>1 >= 2585,5 Вт.
18. Комплекс мощности S>2>:
S>2 >= Ů>cb>I>C>* = Ů>bc>I>C>*; S>2 >= 18981е j-231,42 = 11836,68- j14838,17 ВА.
19. Показание ваттметра W>2> – активная мощность Р>2>:
Р>2 >= ReS>2>; Р>2 >=11836,68Вт.
20. Активная мощность Р, потребляемая источником:
Р = Р>1 >+ Р>2>; Р = 9250,5 Вт.
21. Построить векторную топографическую диаграмму. Векторная топографическая диаграмма строится для всех фаз (рис. 15). Выбираем направления осей +1 и +j. Учтем, что Ů>bс >= 220e j0 = 220 + j0 B. Поэтому вектор фазного напряжения приемника Ů>b>>с >(в выбранном масштабе) направлен по оси +1. К его концу достраивается вектор Ů>а>>b> (с учетом его величины и угла) и т.д. Треугольники векторов токов строятся в вершинах соответствующих точек a, b, c.

Рис. 15 Векторная диаграмма токов и напряжений
Задача № 3.1
Однофазный и трехфазный трансформаторы, работающие как понижающие, имеют примерные параметры, представленные в таблицах 6, 7. Заданы: полная мощность S>н>; номинальные напряжения на первичной U>1н> и вторичной U>2н> обмотках; активные мощности Р>0> в режиме холостого хода и потерь Р>кз> в проводах обмотки при номинальной нагрузке; напряжение короткого замыкания u>ка>.
Таблица 6 .Параметры исследуемых трансформаторов
|
Тип трансформатора |
S>н>, кВА |
U>1н>, В |
U>2н>, В |
Р>0>, Вт |
Р>кз>, Вт |
u>кз>, % |
|
Однофазный |
6,3 |
400 |
230 |
45,2 |
156 |
2,65 |
|
Трехфазный |
25 |
220 |
133 |
157 |
576 |
3,15 |
Таблица 7. Задание к задаче № 3.1
|
>1> |
0,80 |
|
cos>1> |
0,65 |
|
>2> |
0,72 |
|
cos>2> |
0,60 |
Используя параметры трансформаторов необходимо рассчитать:
коэффициент трансформации n;
номинальные токи первичной и вторичной обмотки;
процент активной и реактивной части напряжения короткого замыкания;
напряжение на вторичной обмотке U>2> при активно-индуктивной нагрузке, составляющей >1> от номинальной нагрузки;
значения сos>1>, КПД при cos>2> и нагрузке, составляющей >2> от номинальной;
годовой КПД, если с полной нагрузкой ( = 1) при cos>1> трансформатор работает t>р> = 300 дней в календарном году.
Для условий задачи, соответствующей номеру варианта (таблица 7), выполнить следующие этапы расчета.
1. Записать задание, соответствующее номеру варианта. Письменно пояснить физическое значение параметров S>н>, U>1н>, U>2н>,Р>0>, Р>кз>, u>кз>, I>0,>>1>, соs>1, >>2>, соs>2> (табл. ).
2. Определить (рассчитать) параметры трансформаторов:
Однофазный Трехфазный
3. Коэффициент трансформации n:
n = U>1н>/U>2н>
n =
 1,74;
n
=
1,74;
n
=
1,65.
1,65.
4. Номинальный ток I>1н> первичной обмотки:
для однофазного:
I>1н >= S>н>/U>1н> ;
для трехфазного:
I>1н >= S>н>/3U>1н>:
I>1н
>= 15,75
А; I>1н
>=
15,75
А; I>1н
>=
 65,61
А.
65,61
А.
5. Номинальный ток I>2н> вторичной обмотки:
для однофазного:
I>2н >= S>н>/U>2н> ;
для трехфазного:
I>2н >= S>н>/3U>2н>:
I>2н
>=
 27,4
А; I>2н
>=
27,4
А; I>2н
>=
 108,5
А.
108,5
А.
6. Расчет напряжения на вторичной обмотке U>2> при активно-индуктивной нагрузке.
7. Процент активной части напряжения короткого замыкания u>ка>, %:
резистор катушка напряжение сопротивление
u>ка >= Р>кз>100/S>н>;
u>ка
>=
 2,48
%; u>ка
>=
2,48
%; u>ка
>=
 2,3
%.
2,3
%.
8. Процент реактивной части напряжения короткого замыкания u>кр>, %:
u>кр> = (u>кз>2 − u>ка>2)0,5;
u>кр>
=
0,94 %; u>кр> =
0,94 %; u>кр> =
 2,15
%.
2,15
%.
9. Относительные потери напряженияu>21>, %, при cos>1 >:
u>2 >= >1>(u>ка>cos>1 >+ u>кр>sin>1>);

u>2
>=
 =
1,89 %; u>2
>=
=
1,89 %; u>2
>= =
2,57 %.
=
2,57 %.
10. Относительные потери напряженияu>22>, %, при cos>2 >:
u>2 >= >1>(u>ка>cos>2 >+ u>кр>sin>2>);

u>2
>=
 =
1,79 %; u>2
>=
=
1,79 %; u>2
>= =
2,48 %.
=
2,48 %.
11. Напряжение на вторичной обмотке U>21 >при при cos>1> :
U>21 >= U>2н>(1 u>21>/100);
U>2 >=
 =
225,65 В; U>2
>=
=
225,65 В; U>2
>=
 =
129,58 В.
=
129,58 В.
12. Напряжение на вторичной обмотке U>22 >при при cos>2> :
U>22 >= U>2н>(1 u>22>/100);
U>2 >=
 =
225,88 В; U>2
>=
=
225,88 В; U>2
>= =
129,70 В.
=
129,70 В.
13. Значение КПД при cos>2> и нагрузкой >2>:
= >2>S>н>cos>2>/(>2>S>н>cos>2 >+ P>0 >+ 2>2>P>кз>);
= =
=
=
=
 =0,956
; = 0,959.
=0,956
; = 0,959.
14. Расчет значения годового (за Т = 8760 час) КПД >г >при полной нагрузке.
15. Полезная мощность, отдаваемая трансформатором потребителю электроэнергии при номинальной нагрузке ( = 1) при cos>1>: Р>2н >= S>н>cos>1>;
Р>2н >=
 =
4,01 кВт; Р>2н >=
=
4,01 кВт; Р>2н >=
 =
16,25 кВт.
=
16,25 кВт.
16. Энергия, отдаваемая трансформатором потребителю за год:
W>2 >= Р>2н>t>р>.
t>р>= 7200 час
W>2
>= =
28872 кВтч;
W>2
>=
=
28872 кВтч;
W>2
>= =
180000 кВтч.
=
180000 кВтч.
17. Энергия, потребляемая трансформатором за год в режиме холостого хода:
W>0 >= Р>0>Т;
W>0
>= =
395,95 кВтч;
W>0
>=
=
395,95 кВтч;
W>0
>= =
1375,32 кВтч.
=
1375,32 кВтч.
18. Энергия, теряемая в проводах обмотки трансформатора при номинальной нагрузке за время t>р>:
W>кз >= t>р>P>кз>;
W>кз
>= =
1080 кВтч;
W>кз
>=
=
1080 кВтч;
W>кз
>= =
4147,2 кВтч.
=
4147,2 кВтч.
19. Суммарная энергия, потребляемая трансформатором за год
W = W>2> + W>0> + W>кз>;
W = 28872+395,95 +1080 = 30311,95 кВтч; W = 180000+1375,32 +4147,2 = 185522,52 кВтч.
20. Годовой КПД >г>:
>г> = W>2>/ W;
>г> = =
95,25 %; >г>
=
=
95,25 %; >г>
=
 =
97,02 %.
=
97,02 %.