Основи теорії експлуатації і надійності електронної побутової апаратури
ОСНОВИ ТЕОРІЇ ЕКСПЛУАТАЦІЇ І НАДІЙНОСТІ електронної побутової апаратури (ЕПА)
1. Основні поняття та визначення. Задачі експлуатації
Для підтримання електронної побутової апаратури (як і всієї радіоелектронної апаратури) у справному стані потрібно не тільки досконально знати та володіти нею, а і вміти організовувати та проводити її експлуатацію на наукових основах вирішуючи такі задачі:
- обґрунтування обсягу та змісту робіт і заходів, які проводяться на різних етапах експлуатації;
- розробка методів організації праці обслуговуючого персоналу та технології різних видів робіт у процесі експлуатації;
- визначення складу експлуатаційно-технічних характеристик і показників, які характеризують якість експлуатації;
- розробка критеріїв і методів кількісної оцінки експлуатаційно-технічних характеристик;
- визначення та аналіз факторів, які впливають на якість експлуатації і експлуатаційно-технічних характеристики, а також розробка рекомендацій з покращання експлуатаційно-технічних характеристик;
- розробка основ автоматизації процесу експлуатації;
- дослідження економічних проблем експлуатації та впровадження результатів цих досліджень у практику експлуатації.
Розглянемо ряд основних понять і визначень, які використовуються для характеристики й опису експлуатації.
Експлуатація – це сукупність робіт та організаційних заходів для підтримання електронної побутової апаратури (ЕПА) у постійній технічній справності.
Етап експлуатації – це визначена, закінчена за цільовим призначенням частина процесу експлуатації.
Зазвичай процес експлуатації ЕПА складається з таких основних етапів: зберігання, транспортування, підготовка до застосування, застосування за призначенням, технічне обслуговування, ремонт.
Умови експлуатації – це сукупність факторів, які діють на ЕПА при експлуатації.
До умов експлуатації відносяться кліматичні умови, механічні та електричні навантаження, електромагнітні випромінювання, кваліфікація обслуговуючого персоналу, забезпечення запасними частинами.
Під зберіганням ЕПА розуміється утримання її в технічно справному стані в умовах виробника або споживача протягом установленого терміну до реалізації. У процесі зберігання мають бути створені сприятливі умови утримання техніки, за яких забезпечується зберігання її працездатності.
Транспортування – перевезення ЕПА в умовах, які забезпечують зберігання її працездатності.
Підготовка ЕПА до застосування – це сукупність робіт з підготовки апаратури до нормального функціонування згідно з її призначенням та технічними умовами.
Застосування ЕПА за призначенням – це сукупність робіт, які забезпечують нормальне функціонування апаратури згідно з технічними умовами.
Технічне обслуговування – це комплекс робіт (операцій) для підтримання апаратури у справному або працездатному стані під час підготовки та застосування за призначенням, зберігання і транспортування.
Ремонт – комплекс операцій з поновлення справності або працездатності та поновлення ресурсу ЕПА, або складових частин.
Ресурсом називають напрацювання виробу в годинах від початку експлуатації до настання граничного стану, коли подальша експлуатація електронної апаратури небезпечна або економічно недоцільна.
Якщо розглянути всі електронні апарати, то в залежності від ступеня старіння, характеру несправності, від складності та обсягу робіт ремонт поділяють на плановий і неплановий. Плановим називають ремонт, постановка на який здійснюється відповідно до вимог нормативно-технічної документації.
Неплановий – це ремонт, який здійснюється без попереднього призначення.
Ремонт, який виконується для забезпечення або поновлення працездатності апаратури та полягає в заміні або поновленні її окремих модулів, називається поточним. Він здійснюється після виникнення відмови і може виконуватися на місці знаходження радіоелектронної апаратури.
Ремонт, який виконується для поновлення справності та часткового поновлення ресурсу ЕПА з заміною або поновленням складових частин обмеженої номенклатури і контролем технічного стану складових частин в обсязі відповідно до нормативно-технічної документації, називають середнім.
Ремонт, який виконується для поновлення справності та повного або близького до повного поновлення ресурсу апарата з заміною або поновленням будь-яких його частин, включаючи базові, називають капітальним.
Експлуатація електронної побутової апаратури має деякі особливості. Так, підготовка до застосування її включає передпродажну підготовку, установку та регулювання апаратури після купівлі дома у власника. Передпродажна підготовка передбачає підготовку апаратури до роботи, перевірку її працездатності (за необхідності регулювання та налагодження), а також призначений 2-годинний електропрогін апаратури в магазині з 4-ма відключеннями від електромережі.
Друга особливість полягає в тому, що в період між технічним обслуговуванням та ремонтом апаратуру експлуатує сам споживач, тобто застосування за призначенням здійснює власник апаратури. Оскільки апаратура не має абсолютної надійності, то за цей період експлуатації виникають несправності і відбувається вихід параметрів пристроїв за межі припусків. Наведені обставини вимагають створення спеціальних ремонтних органів і проведення відповідного періодичного технічного обслуговування ЕПА у будинку власника апаратури.
Задачами експлуатації електронної апаратури є: організація та проведення заходів, що забезпечують підготовку до використання, використання за призначенням, підтримання справного стану.
Під експлуатаційними властивостями ЕА розуміють її надійність, готовність до використання основних функцій, пристосованість до технічного обслуговування, економічність.
Розглянемо ці властивості.
Надійність – це властивість об’єкта виконувати задані функції, зберігаючи при цьому протягом часу значення встановлених експлуатаційних показників в заданих межах, що відповідають заданим режимам і умовам використання, технічного обслуговування, ремонту, зберігання та транспортування.
Готовність – це властивість об’єкта, яка характеризує його пристосованість до переведення з будь-якого початкового стану до стану безпосереднього застосування за призначенням.
Пристосованість до технічного обслуговування – це властивість апаратури ефективно виконувати завдання, які постають перед нею під час проведення технічного обслуговування із заданою тривалістю та визначеною періодичністю.
Економічність – це властивість, яка характеризує витрати, пов’язані з експлуатацією електронної апаратури.
Надійність є однією з найважливіших експлуатаційних властивостей, оскільки вона значною мірою визначає ефективність застосування апаратури до призначення, а також потрібний рівень надійності визначає і вартість виготовлення ЕА.
Надійність є комплексною властивістю. В залежності від призначення ЕА та умов експлуатації надійність може включати безвідмовність, ремонтоздатність, здатність до зберігання та довговічність.
Безвідмовність – це властивість конструкції (апаратури) зберігати працездатність протягом деякого часу або деякого напрацювання. При цьому під працездатним станом розуміють такий стан ЕА, при якому апаратура спроможна виконувати задані функції, зберігаючи значення заданих параметрів в межах, встановлених нормативно-технічною документацією. Якщо значення хоча б одного заданого параметра не відповідає встановленим вимогам, то апаратура знаходиться у непрацездатному стані.
В процесі експлуатації ЕА може транспортуватися, а також зберігатися інколи протягом тривалого часу.
Властивість апаратури безперервно зберігати справний і працездатний стан протягом та після зберігання, транспортування називають здатністю до зберігання.
Основним показником здатності до зберігання є термін служби зберігання – календарна тривалість зберігання і транспортування апаратури в заданих умовах, протягом і коли закінчиться термін, зберігаються в установлених границях показники призначення.
Довговічність – це властивість ЕА зберігати працездатність до настання граничного стану при встановленій системі технічного обслуговування та ремонтів.
Граничним називають такий стан, при якому подальша експлуатація ЕА має бути припинена за таких причин:
- якщо неможливо ліквідувати порушення вимог безпеки;
- якщо неможливо ліквідувати вихід заданих параметрів за встановлені границі;
- якщо неможливо ліквідувати зниження ефективності експлуатації нижче припустимого.
Ознаки граничного стану встановлюються нормативно-технічною документацією.
Показники довговічності пов’язані з поняттям ресурсу та терміну служби.
Терміном служби називають тривалість експлуатації ЕА від її початку до настання граничного стану, тобто безперервний (календарний) час, відрахований незалежно від тривалості фактичного включеного стану апаратури в цей період. Термін служби вимірюється роками.
Більш широким поняттям, яке характеризує технічний стан ЕА, є поняття „справний стан”.
Під справним станом розуміють такий стан ЕА, при якому він відповідає всім вимогам, встановленим нормативно-технічною документацією. З цього визначення зрозуміло, що поняття „справність” набагато ширше, ніж „працездатність”, оскільки апаратура може бути і несправною, але працездатною (тобто задовольняти вимогам забезпечення виконання заданих функцій), якщо вона не відповідає тим вимогам, які не впливають на якість її функціонування. Якщо ЕПА не відповідає хоча б одній з вимог, встановлених нормативно-технічною документацією, вона вважається несправною.
Перехід апаратури з одного стану в інший називається подією. Подія, яка полягає в порушенні працездатності апаратури, називається відмовою. Як випливає з визначення, під відмовою слід розуміти не тільки повну втрату працездатності, але й її погіршення внаслідок зміни значення параметрів.
Відмови підрозділяють:
- за характером зміни параметрів до моменту виникнення відмови – на раптові та поступові.
Раптовими називають відмови, які характеризуються стрибкоподібною зміною одного або декількох заданих параметрів. Поступовою називають відмову, яка характеризується поступовою зміною значення одного або декількох заданих параметрів;
- за взаємозв’язком між собою – на залежні та незалежні.
Залежною називають відмову одного елемента пристрою, обумовлену відмовою другого елемента.
Незалежною називають відмову елемента пристрою, не обумовлену відмовою інших елементів;
- за характером часу порушення працездатності – на збої та перемежовуючі відмови.
Збоєм називають відмови, які самоліквідуються та призводять до короткочасного порушення працездатності.
Перемежовуючою відмовою називають багаторазове виникнення збою одного й того самого характер;
- за наявності зовнішньої ознаки – на явні та неявні.
Явна – це відмова, яка виявляється відразу після її появи без застосування вимірювальних приладів.
Неявна (прихована) – це відмова, яка не має зовнішніх ознак прояву та може бути виявлена тільки за допомогою вимірювальних приладів;
- за причиною виникнення – на конструкційну, виробничу, експлуатаційну.
Конструкційною називають відмову, яка виникає в результаті порушення правил або норм конструювання апаратури.
Виробничою називають відмову, яка виникає в результаті порушення встановленого технологічного процесу виготовлення або ремонту апаратури.
Експлуатаційною називають відмову, яка виникає в результаті порушення встановлених правил або умов експлуатації апаратури.
Наведемо у вигляді структурної схеми класифікацію видів відмов радіоелектронної апаратури.
експлуатація побутова апаратура технічний

Рисунок 1 – Класифікація видів відмов
Крім того, вся електронна апаратура, її складові частини поділяються на ті, що підлягають ремонту, і ті, що не підлягають ремонту.
Апаратура, яка підлягає ремонту – це така, справність і працездатність якої у випадку виникнення відмови або пошкодження підлягає поновленню.
Апаратура, у якої справність та працездатність не підлягає поновленню, називається такою, що не підлягає ремонту.
Під ремонтопридатністю розуміють властивість ЕА, що полягає в пристосуванні до попередження та виявлення причин виникнення її відмов, пошкодження і поновлення працездатного стану шляхом проведення технічного обслуговування та ремонту.
2. Експлуатаційно-технічні показники
Розглянуті раніше поняття та визначення є якісними характеристиками. Для кількісного виразу надійності, готовності та економічності використовуються експлуатаційно-технічні показники.
Вибір можливого переліку показників проводять з урахуванням певних вимог. Це такі вимоги:
- можливість оцінювати відповідні характеристики в різних умовах і на різних етапах експлуатації;
- можливість їх числового визначення або завдання;
- можливість їх розрахунку за даними експлуатації і проектування;
- достатня універсальність;
- простота та зручність застосування.
У залежності від умов отримання потрібних для розрахунку даних показники називають: оціночними, експериментальними, прогнозованими екстрополірованими.
Щоб оцінити експлуатаційні властивості ЕА, застосовують показники безвідмовності, ремонтопридатності, довговічності, готовності, здатності до зберігання та експлуатаційно-економічні.
Показники безвідмовності для неремонтованої апаратури:
- ймовірність безвідмовної
роботи –

- частота відмов –
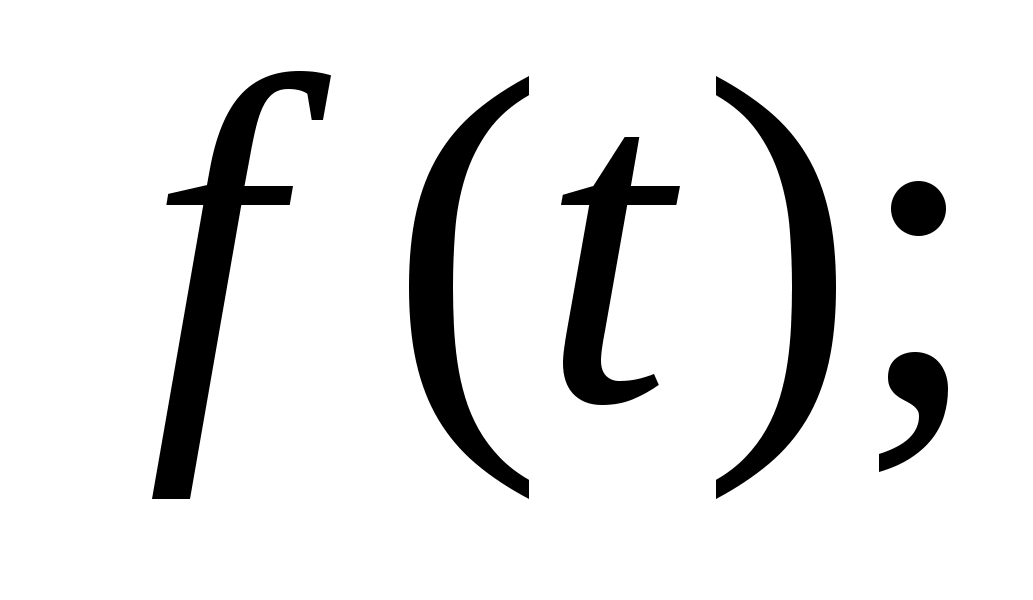
- інтенсивність відмов
–

- середнє напрацювання
до відмови –
 .
.
1 Показники безвідмовності для ремонтованої апаратури:
- ймовірність безвідмовної
роботи –

- параметр потоку
відмов –

- інтенсивність відмов
–

- середнє напрацювання
на відмову –
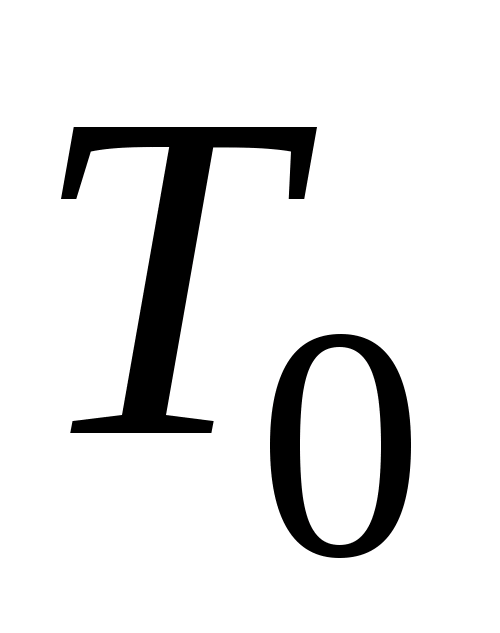 .
.
Показники ремонтопридатності:
- середня тривалість
поточного ремонту –

- середня тривалість
технічного обслуговування –
 .
.
Показники довговічності для неремонтованої апаратури:
- середній термін
(строк) служби –

- середній термін
служби до списування –

- гамма-відсотковий
термін служби –
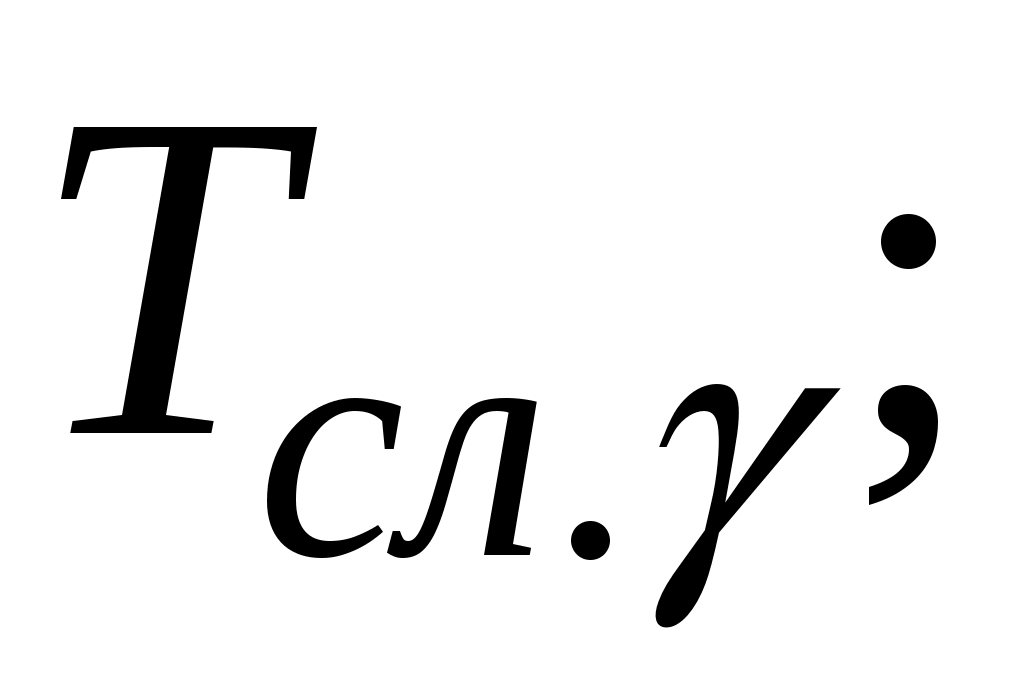
- середній ресурс –
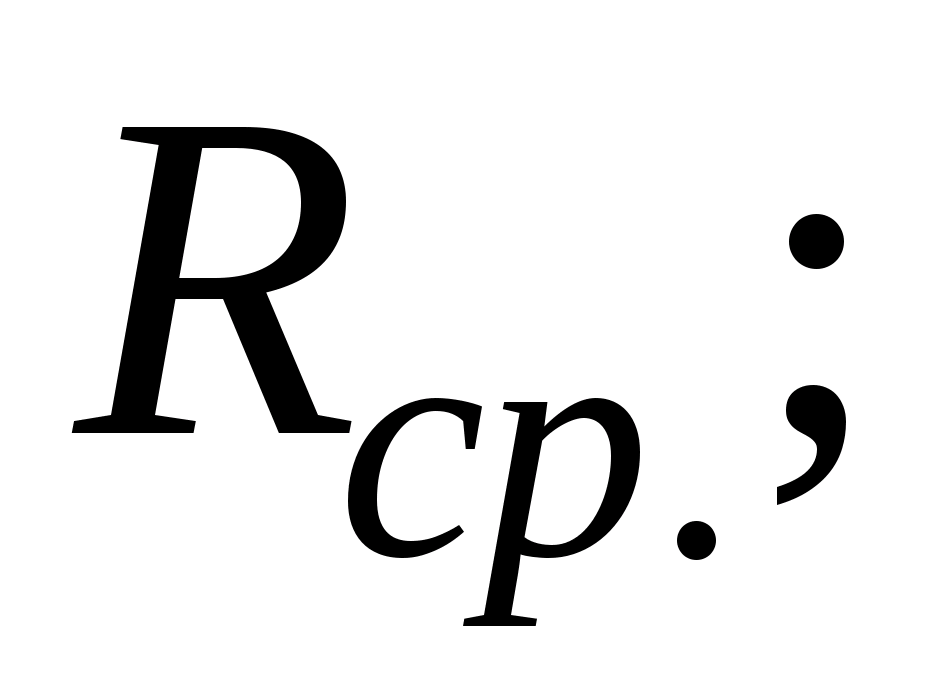
- призначений ресурс
–

- гамма-відсотковий
ресурс –
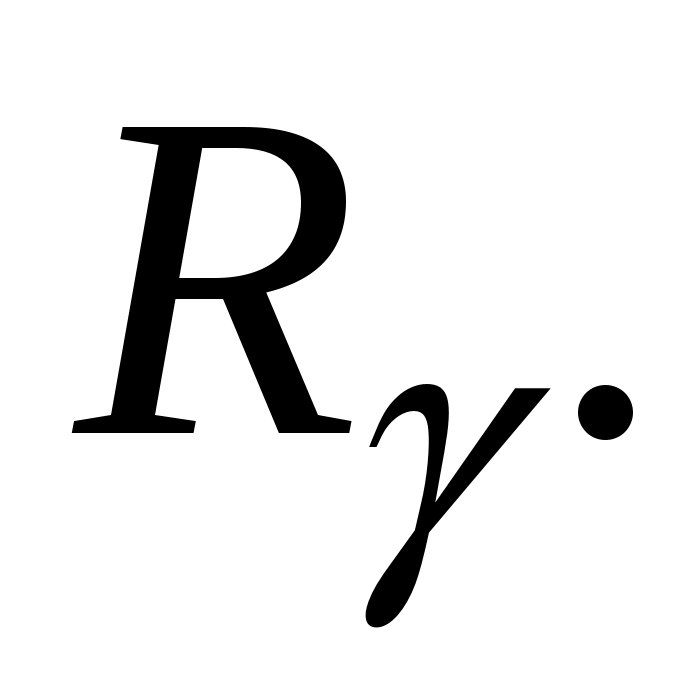
3.1 Показники довговічності для ремонтованої апаратури:
- середній термін
служби –

- середній термін
служби до списування –

- гамма-відсотковий
термін служби –
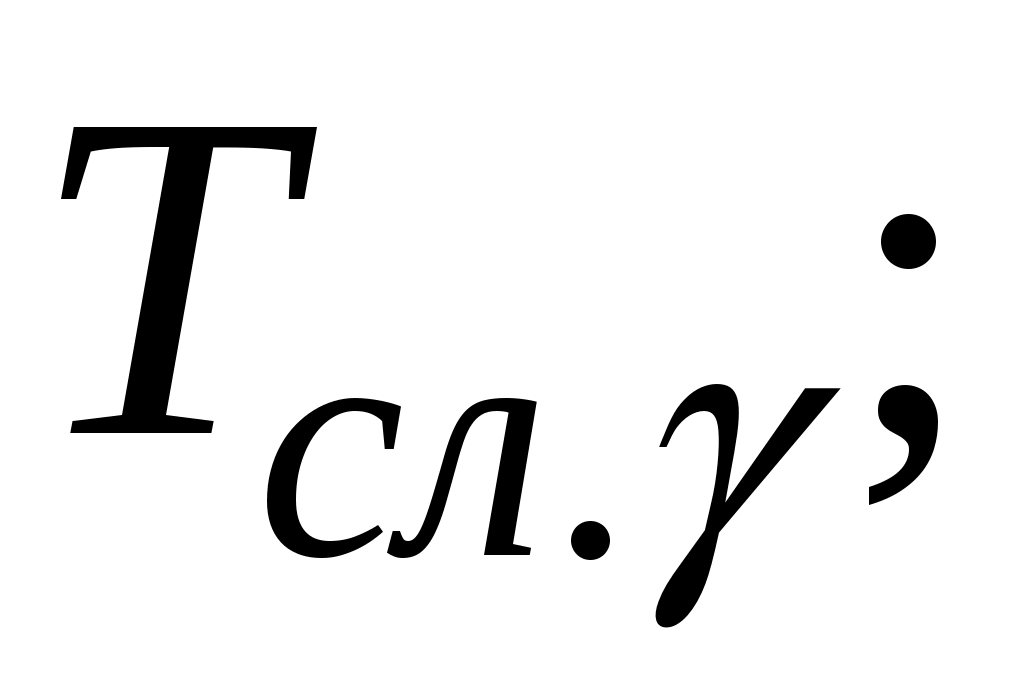
- середній термін
служби до капітального (середнього)
ремонту –
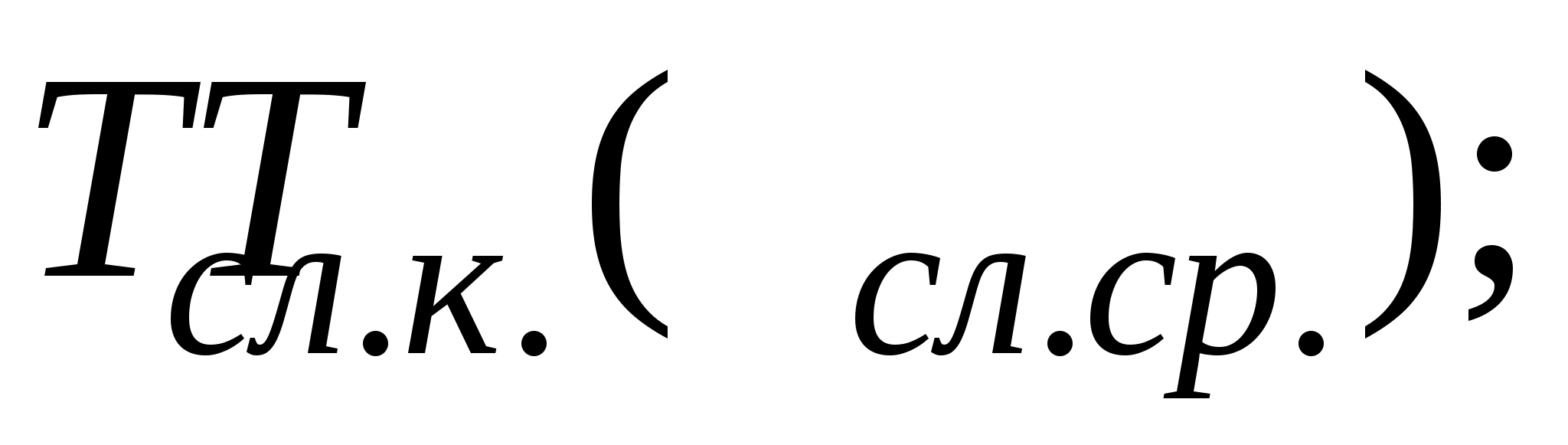
- середній термін
служби між капітальними (середніми)
ремонтами –
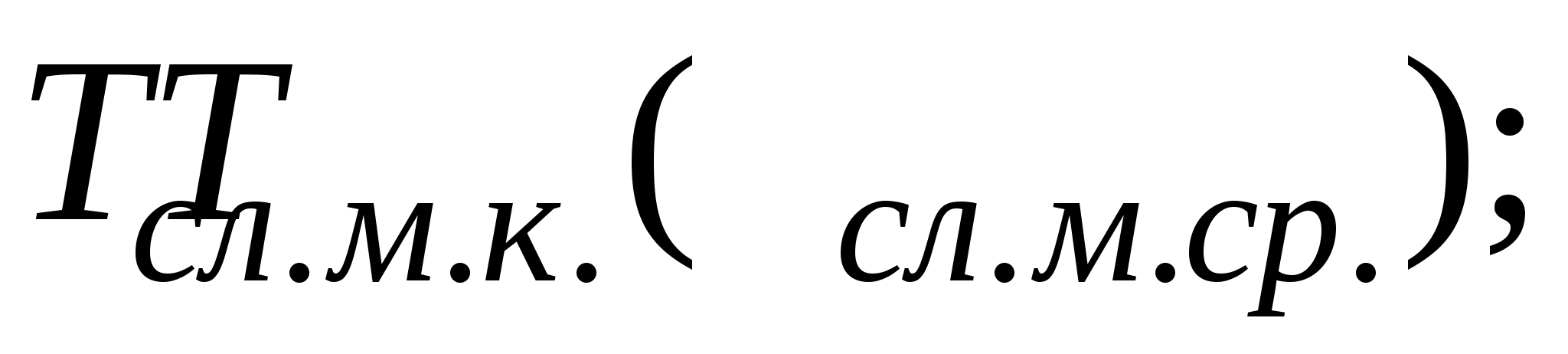
- середній ресурс –
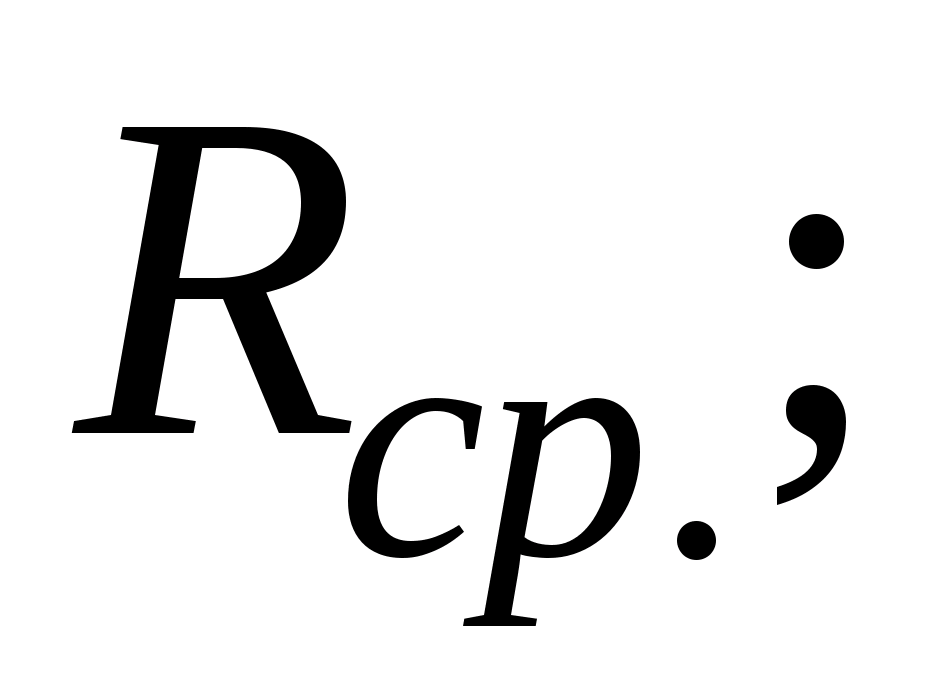
- призначений ресурс
–

- гамма-відсотковий
ресурс –
 ;
;
- середній ресурс до
капітального (середнього) ремонту –

- середній ресурс між
капітальними (середніми) ремонтами –
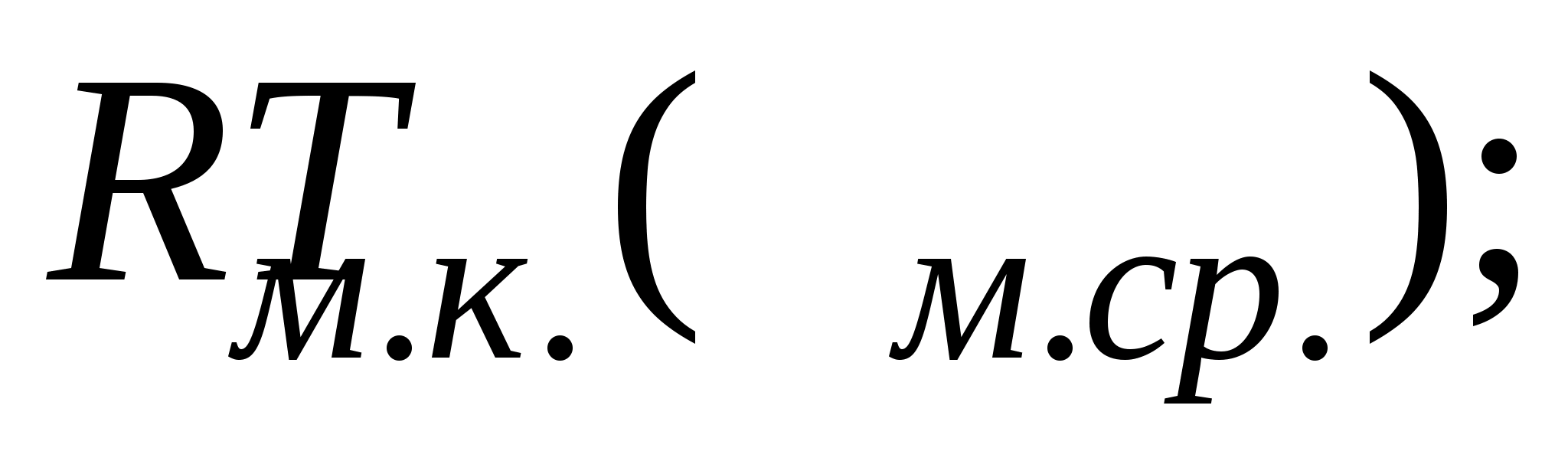
- середній ресурс до
списання –

Показники здатності до зберігання:
- середній термін
зберігання –

- гамма-відсотковий
термін зберігання –

Показники готовності:
- коефіцієнт готовності
–

- коефіцієнт оперативної
готовності –

- коефіцієнт технічного
використання –
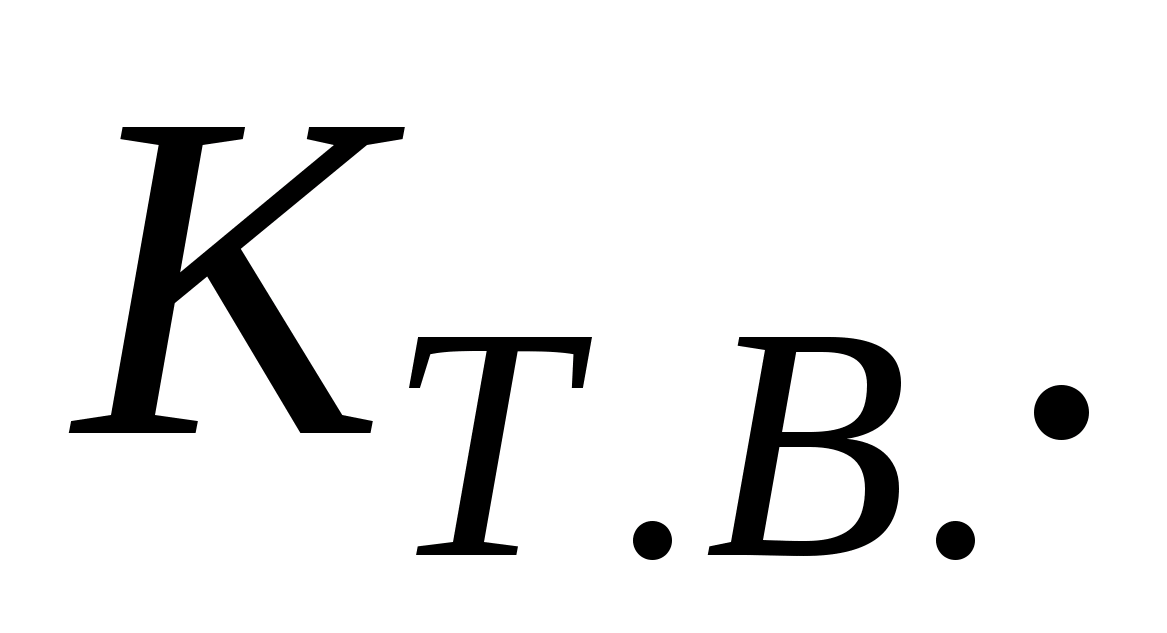
Експлуатаційно-технічні показники:
- середня трудомісткість
поточного ремонту –
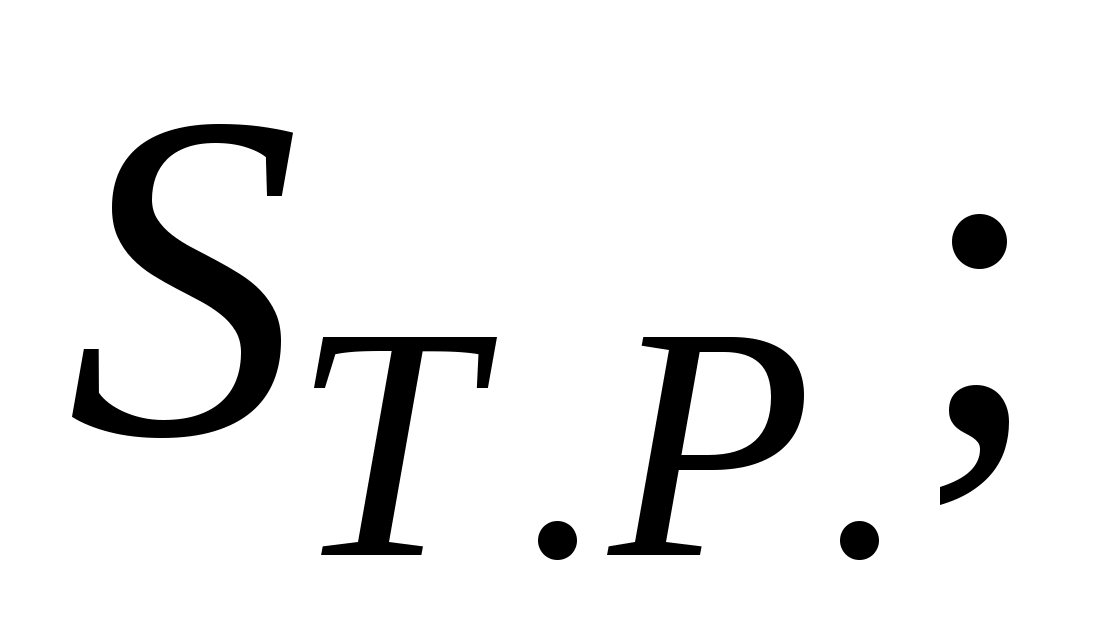
- середня трудомісткість
технічного обслуговування –

- коефіцієнт вартості
експлуатації –

3. Основні поняття теорії ймовірності
Виникнення відмов в ЕА залежить від різних факторів, які визначаються як внутрішніми властивостями апаратури, так і діями зовнішніх умов. Це призводить до того, що процес виникнення відмов, а також інші характеристики ЕА у процесі експлуатації носять випадковий характер. Тому для кількісної оцінки різних характеристик ЕА широко використовуються імовірнісні методи.
У теорії ймовірності випадковою називається величина, яка в результаті експерименту може прийняти те або інше значення, передбачити яке заздалегідь вірогідно неможливо. Всі випадкові величини поділяються на безперервні та дискретні. Прикладами безперервних випадкових величин є час безвідмовної роботи пристрою, значення того або іншого технічного параметра тощо.
Дискретними випадковими величинами є кількість відмов, які виникають за деякий період роботи пристрою, кількість несправних елементів, пристроїв тощо.
Подією в теорії ймовірності визначається будь-який факт, який у результаті експерименту може статися або не статися. Для кількісного порівняння подій між собою за ступенем їх можливості використовують визначене число, яке тим більше, чим більш можлива подія. Таке число називають ймовірністю події.
Якщо ймовірність однієї події не змінюється від того, відбулась чи ні друга подія, то така подія називається незалежною. Якщо ж можливість появи однієї події залежить від того, відбулась чи ні друга подія, то такі події називають залежними. Події називаються несумісними, якщо ніякі дві з них не можуть з’явитися разом.
Подію, ймовірність якої дорівнює одиниці, називають вірогідною подією. Подію, ймовірність якої близька до одиниці, називають практично ймовірною.
На основі введеного поняття розглянемо основні теореми теорії ймовірності, які широко застосовуються під час вирішення багатьох задач надійності.
3.1 Теореми додавання та множення ймовірностей
Ймовірність суми n несумісних подій дорівнює сумі ймовірностей цих подій:
 .
(1)
.
(1)
Ймовірність добутку незалежних подій дорівнює добутку ймовірностей цих подій:
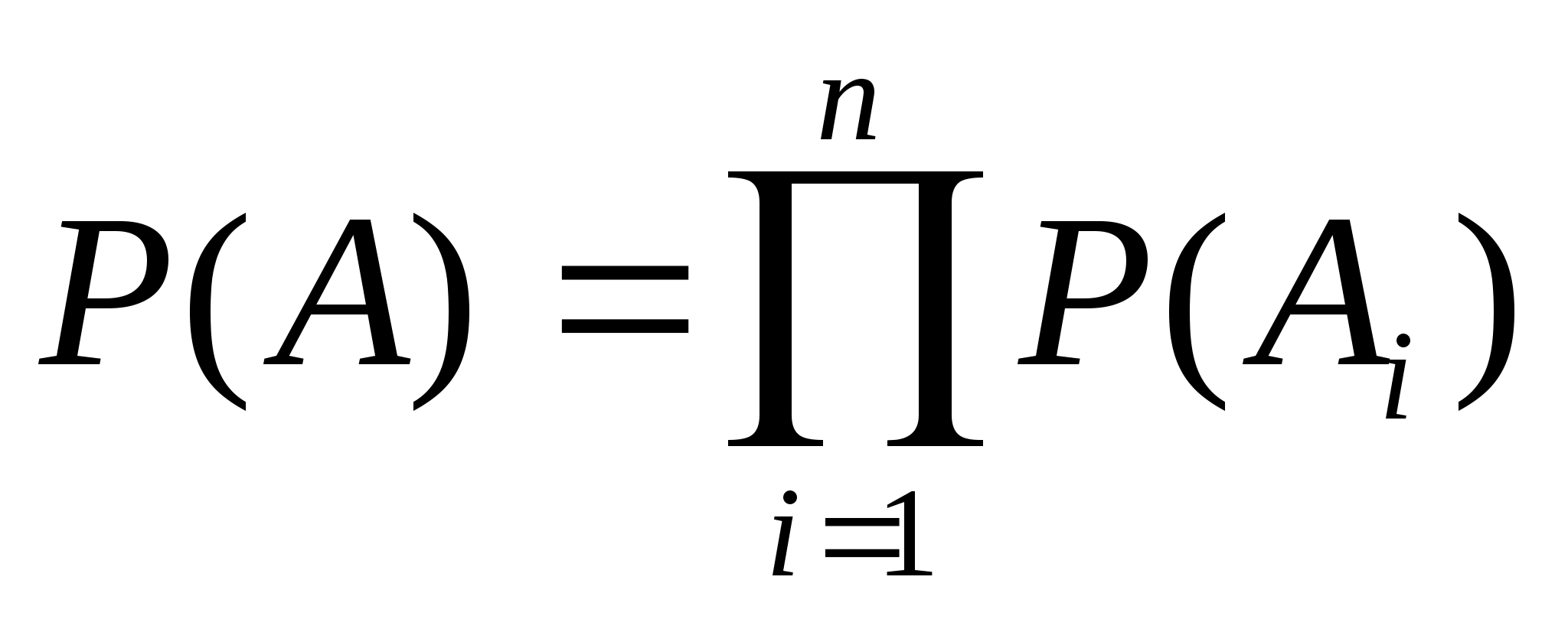 .
(2)
.
(2)
На практиці рідко зустрічаються задачі, в яких потрібно застосовувати тільки теорему додавання або тільки теорему множення ймовірностей. Як правило, ці теореми застосовують спільно.
3.2 Теорема повної ймовірності
На основі теореми додавання та множення формулюється теорема повної ймовірності.
Нехай потрібно визначити
ймовірність деякої події А, яка може
відбутися разом з однією з подій
 ,
що утворюють групу несумісних подій,
які називаються гіпотезами:
,
що утворюють групу несумісних подій,
які називаються гіпотезами:
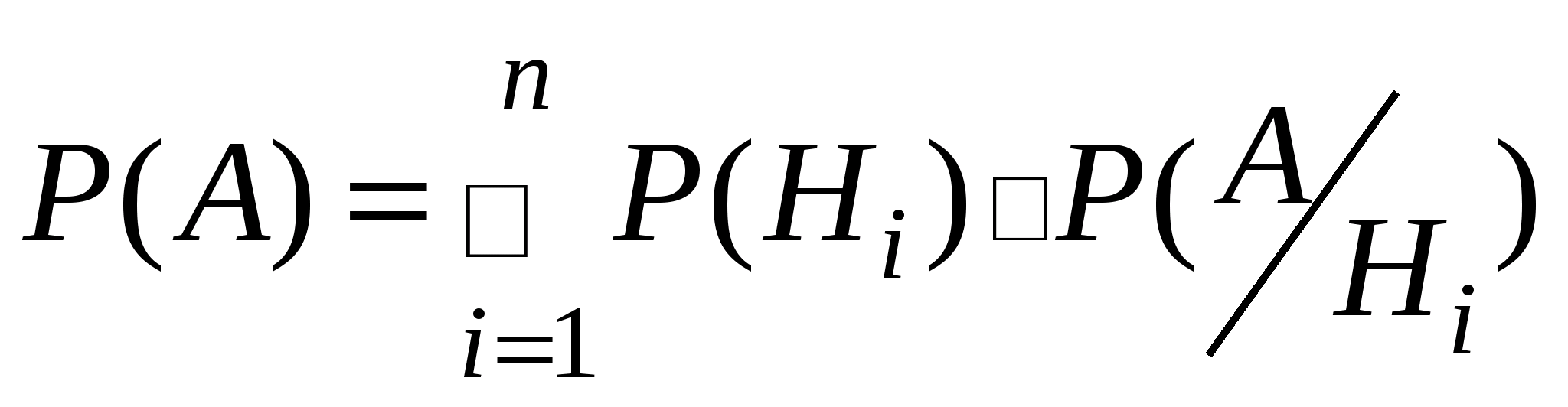 ,(3)
,(3)
тобто ймовірність події А знаходиться як сума добутків ймовірностей кожної гіпотези на ймовірність події при цій гіпотезі.
3.3 Закони розподілу випадкової величини
Законом розподілу випадкової величини називають співвідношення, яке встановлює зв’язок між можливим значенням випадкової величини та відповідними їм ймовірностями. Вважають, що випадкова величина в цьому випадку підпорядкована даному закону розподілу.
Інтегральним законом розподілу або функцією розподілу називається функція виду:
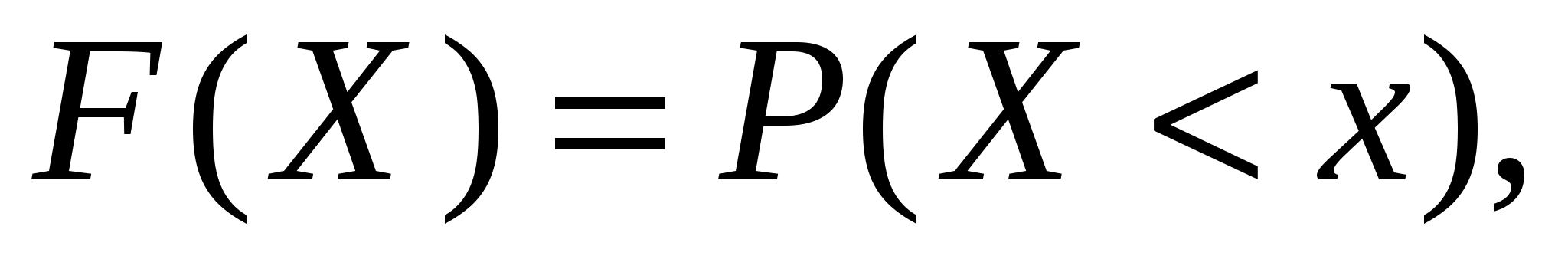 (4)
(4)
де x – деяка поточна змінна.
Функція розподілу – універсальна характеристика випадкової величини. Вона існує як для перервних, так і безперервних величин і характеризує ймовірність події Х<x. Функція розподілу має такі властивості:
функція розподілу F(x) є функція, яка не зменшується від свого аргументу, тобто при х>2>>x>1>, F(x>2>)≥F(x>1>);
на мінус нескінченності функція розподілу дорівнює нулю F(-∞)=0;
на плюс нескінченності функція розподілу дорівнює одиниці F(∞)=
Нехай маємо випадкову величину Х з функцією розподілу F(x), яку припускаємо безперервною та диференційованою. Обрахуємо ймовірність натрапляння цієї випадкової величини у відрізок від х до х+Δх. Умовимося лівий кінець відрізку х включати в інтервал х, х+Δх, а правий – не включати. Тоді потрапляння випадкової величини Х у відрізок х, х+Δх рівносильне виконанню нерівності:

Виразимо ймовірність цієї події через F(x). Для цього розглянемо три події:
подія А полягає в тому, що Х<x+Δx;
подія В полягає в тому, що Х<x;
подія С полягає в тому, що х≤ Х<x+Δx.
Враховуючи, що А=В+С, згідно з теоремою додавання ймовірностей отримаємо:
 або
або
 звідки
звідки
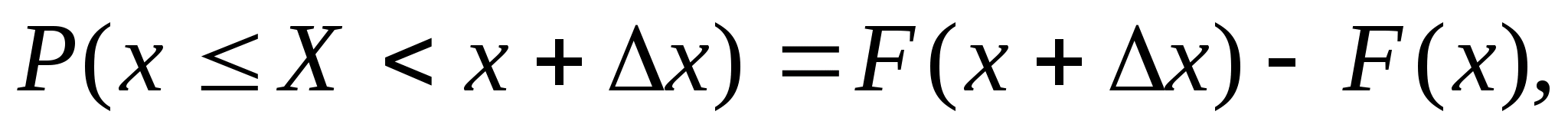
тобто отримати приріст функції розподілу на цьому відрізку.
Отже, ймовірність потрапляння випадкової величини у заданий інтервал дорівнює приросту функції розподілу на цьому інтервалі.
Розглянемо відношення (частку) цієї ймовірності до довжини інтервалу та наближатимемо Δx до нуля.
На границі ми отримаємо похідну від функції розподілу:
 (5)
(5)
Функція f(x) – похідна функції розподілу, характеризує щільність, з якою розподіляється значення випадкової величини у даній точці. Ця функція називається щільністю розподілу або диференціальним законом розподілу величини Х. Щільність розподілу є однією з форм закону розподілу. На противагу функції розподілу щільність існує тільки для безперервних випадкових величин.
Кожен закон розподілу являє собою деяку функцію, яка повністю описує випадкову величину з імовірнісної точки зору. Проте часто на практиці немає необхідності характеризувати випадкову величину повністю, буває достатньо лише знати окремі числові параметри. Такі параметри, які характеризують у стислій формі істотні особливості розподілу, називаються числовими характеристиками випадкової величини. Основними числовими характеристиками випадкових величин, які вивчають у надійності, є математичне сподівання або середнє значення та дисперсія.
Для перервної величини Х математичним сподіванням називається сума добутків усіх можливих значень випадкової величини на ймовірність цих значень:
 (6)
(6)
Для безперервної величини Х математичне сподівання виражається вже не сумою, а інтегралом:
 (7)
(7)
де f(x) – щільність розподілу величини Х.
Дисперсія випадкової величини Х є характеристика розсіяності, тобто розкидання значень випадкової величини біля її математичного сподівання.
Відповідно для перервних і безперервних випадкових величин маємо:
 (8)
(8)
 (9)
(9)
Величина, отримана добуванням квадратного кореня з дисперсії, називається середньоквадратичним відхилом випадкової величини Х від математичного сподівання:
 (10)
(10)
На практиці часто доводиться визначати числові характеристики випадкової величини за обмеженим об’ємом статистичних даних про відмови, яких замало, щоб судити про закон розподілу випадкової величини. У цьому випадку знаходять статистичні характеристики (оцінки):
- статистичне математичне сподівання (середнє значення):
 (11)
(11)
- статистичну дисперсію:
 (12)
(12)
- дисперсію математичного сподівання:
 (13)
(13)
- дисперсію дисперсії:
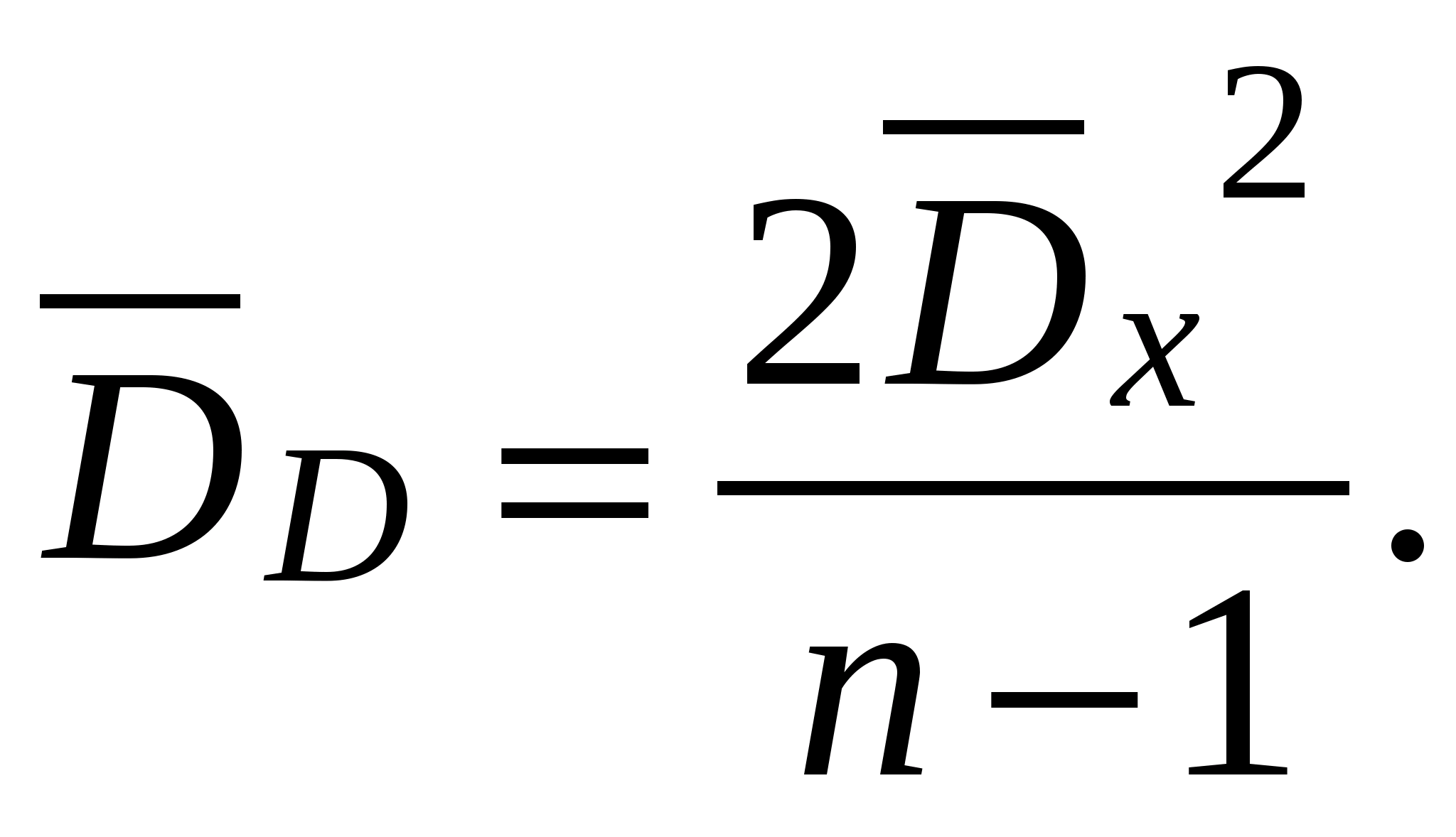 (14)
(14)
4. Елементи теорії масового обслуговування
Процес виникнення відмов у роботі ЕА, організація та проведення її ремонту, постачання запасними елементами, матеріалами та інші ситуації в теорії та практиці експлуатації ЕА можуть бути описані методами теорії масового обслуговування.
Системою масового обслуговування називається система, яка складається з деякого числа обслуговуючих одиниць, які називаються каналами обслуговування. Системи масового обслуговування можуть бути одноканальними та багатоканальними. Основними елементами системи масового обслуговування є: потік подій, кількість каналів та швидкодія кожного каналу. Під потоком подій розуміють послідовність подій, які проходять одна за одною в деякі моменти часу. Потік подій називається найпростішим, якщо він має властивість ординарності, стаціонарності та відсутність післядії.
Ординарність потоку означає, що ймовірність появи двох і більше подій за один і той самий момент часу практично відсутня.
Стаціонарність потоку означає, що ймовірність тієї або іншої кількості подій на відрізок часу довжиною t=Δt не залежить від t і залежить тільки від довжини відрізку Δt.
Відсутність післядії полягає в тому, що для двох відрізків часу Δt>1> і Δt>2> кількість подій, які потрапляють в один з них, не залежить від кількості подій, які потрапляють в другий.
Режим роботи системи
масового обслуговування залежить також
від характеристик продуктивності самої
системи: кількості каналів і продуктивності
кожного каналу. Однією із найважливіших
величин, пов’язаних з системою, є
середній час обслуговування однієї
заявки

У практиці найбільшого
поширення набув випадок, коли величина
 має експоненціальний розподіл:
має експоненціальний розподіл:
 (15)
(15)
де
 – величина, зворотна середньому часу
обслуговування однієї заявки.
– величина, зворотна середньому часу
обслуговування однієї заявки.
Системи масового обслуговування поділяються на два основних типи: системи з відмовами та системи з очікуванням. У системах з відмовами заявка, яка надійшла в момент, коли всі канали обслуговування зайняті, негайно отримує відмову, залишає систему і в подальшому процесі обслуговування не бере участі.
У системах з очікуванням заявка, яка застала всі канали зайнятими, не залишає системи, а стає в чергу і очікує, поки не звільниться який-небудь канал.
Процес експлуатації електронної побутової апаратури (заявки на ремонт, постачання запасних елементів тощо) може бути найбільш повно описаний тільки з використанням теорії масового обслуговування з очікуванням.
Нехай у системі є n
каналів. На вхід системи надходить
найпростіший потік заявок з інтенсивністю
(щільністю) λ. Середній час обслуговування
однієї заявки
 – експоненціальний з параметром
– експоненціальний з параметром
 .
Середня кількість заявок α>3>=λ
.
Середня кількість заявок α>3>=λ Час очікування не обмежений.
Час очікування не обмежений.
Стан системи масового обслуговування нумеруватимемо за кількістю заявок:
S>0> – CMO вільна;
S>1> – зайнятий один канал;
S>2> – зайняті два канали;
- - - - - - - - - - - - - - - - - черги немає
S>n> – зайняті всі канали;
S>n+1 >– зайняті всі n каналів, одна заявка знаходиться у черзі;
S>n+r >– зайняті всі n каналів, r заявок знаходяться у черзі.
Тоді для розрахунку ймовірності стану системи при встановленому режимі обслуговування (тобто де кількість заявок α>3> менше кількості каналів n, α>3><n) можна користуватися формулою:
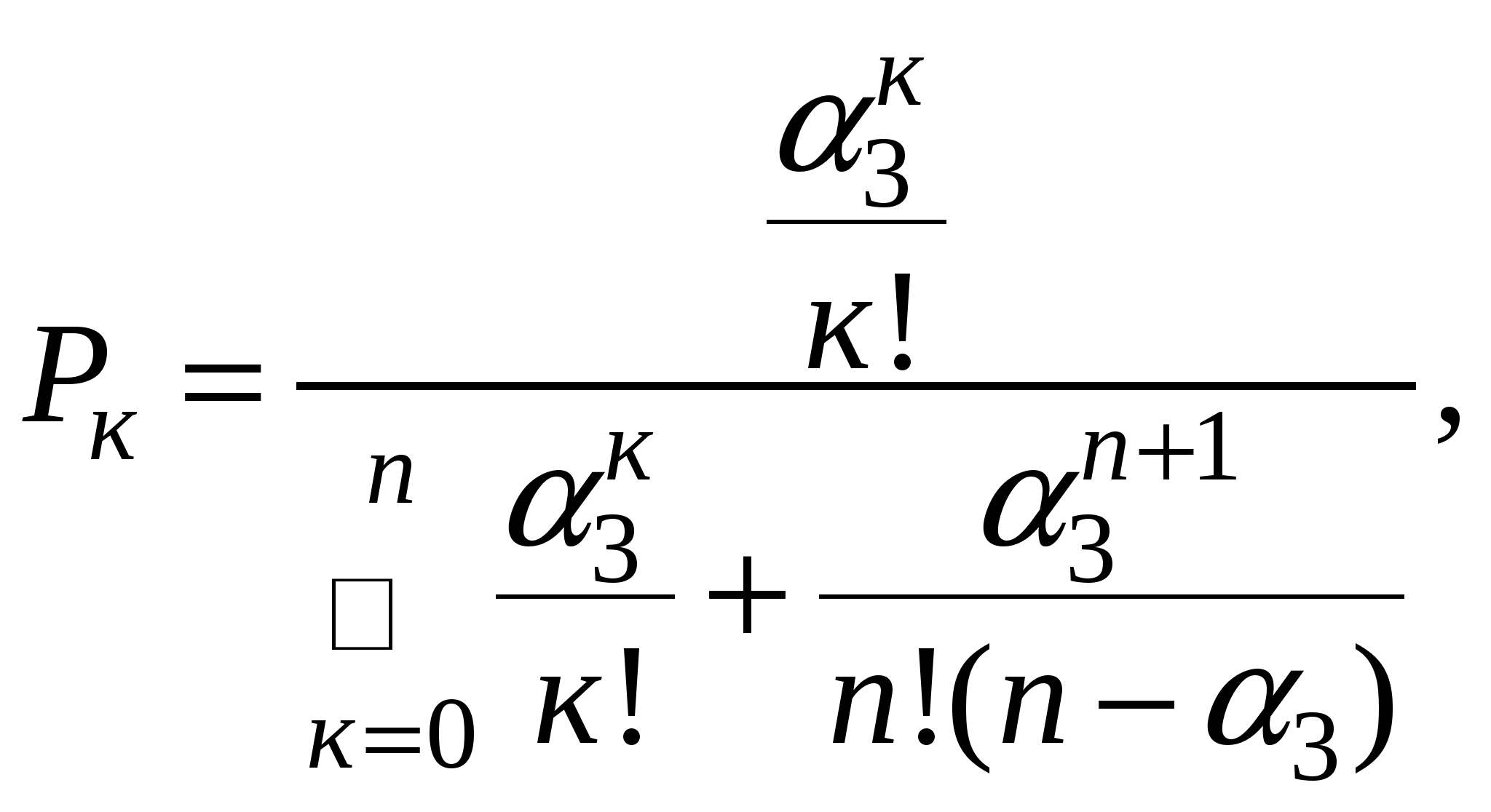 (16)
(16)
де к – число станів системи (0≤к≤n).
Ймовірність наявності черги:
 (17)
(17)
Середнє число заявок, які знаходяться в черзі:
 (18)
(18)
Тепер можна знайти середній час перебування заявки в черзі:
 (19)
(19)
де λ – інтенсивність заявок за годину.