Метод статистической стабилизации частот независимо функционирующих генераторов

Содержание

Основная часть

выводы

Библиографический список

Основная часть

Расширение круга задач, решаемых современными системами, сетями и устройствами телекоммуникаций, внедрение новых технологий и достижение принципиально новых возможностей при их создании и развитии стимулировало в последние десятилетия интенсивное развитие способов и методов стабилизации параметров генераторов, включая также методы повышения стабильности частот генераторов. Такое внимание к данному научному направлению в значительной степени определяется тем влиянием, которое оказывает стабильность формируемых в радиоэлектронных системах частот на качественные показатели систем и устройств телекоммуникаций.

Основные области использования систем, сетей и устройств телекоммуникаций представляют собой каналы и линии связи, включающие устройства, системы и сети для организации единичного, группового, регионального и глобального информационного обмена. Перечень вопросов, возникающих при проведении исследований в данном направлении, включает исследования, разработку, проектирование и эксплуатацию систем, сетей и устройств, обеспечивающих обмен информацией между абонентами. При этом наиболее важной составляющей в данной совокупности вопросов являются собственно научные, технические и технологические разработки систем, сетей и устройств телекоммуникаций различного типа. Актуальным направлением является разработка новых принципов построения и работы устройств телекоммуникаций для генерации, передачи и приема.

Функционирование устройств телекоммуникаций различного назначения, включая радиотехнические, акустические, лазерные, волоконно-оптические системы и другие, невозможно без обеспечения требуемой стабильности частот [1–6]. При этом основным фактором, определяющим высокую эффективность функционирования систем, сетей и устройств телекоммуникаций, является обеспечение требуемой стабильности частот. Это связано с тем, что именно от стабильности частот генераторов зависит точность определения длительности временных отрезков и фаз сигналов, лежащих в основе организации информационного обмена.

Необходимость существенного повышения стабильности частот колебаний, формируемых в радиотехнических, акустических, лазерных и других системах телекоммуникаций зачастую диктует требования к характеристикам стабильности генераторов, практически невыполнимые при традиционном подходе к решению задач и их построении. В связи с этим возникает необходимость поиска методов и алгоритмов для повышения стабильности частот генераторов, требующие принципиально новых идей.

Функционирование устройств телекоммуникаций различного назначения, включая радиотехнические, акустические, лазерные, волоконно-оптические системы и другие, невозможно без обеспечения требуемой стабильности частот [1–3]. При этом основным фактором, определяющим высокую эффективность функционирования систем, сетей и устройств телекоммуникаций, является обеспечение требуемой стабильности частот. Это связано с тем, что именно от стабильности частот генераторов зависит точность определения длительности временных отрезков и фаз сигналов, лежащих в основе организации информационного обмена.

Необходимость существенного повышения стабильности частот колебаний, формируемых в радиотехнических, акустических, лазерных и других системах телекоммуникаций, зачастую диктует требования к характеристикам стабильности генераторов, практически невыполнимые при традиционном подходе к решению задач и их построении. В связи с этим возникает необходимость поиска методов и алгоритмов для повышения стабильности частот генераторов, требующих принципиально новых идей.

Радиоэлектронная аппаратура, входящая в состав большинства устройств и систем телекоммуникаций, может содержать большое число (которое в дальнейшем будем обозначать ) высокочастотных генераторов. Данные генераторы могут формировать сигналы с различной временной структурой , иметь различную относительную нестабильность и функционировать независимо на частотах, которые не связаны между собой. В частности, если генератор формирует гармонические сигналы с частотой , то выходной сигнал имеет вид . При формировании последовательностей с импульсами прямоугольной формы выходной сигнал имеет вид:

где – функция Хевисайда.

В большинстве рассматриваемых радиоэлектронных систем сигналы от каждого из генераторов или поступают на какое-то общее устройство, или могут быть легко на него выведены. Это позволяет получать данные об отклонениях частот каждого из генераторов от номинальных значений в некоторый момент времени или данные об отклонениях фаз сигналов каждого из генераторов от номинальных значений за некоторый интервал времени. Далее с использованием полученных данных проводится формирование сигналов управления для стабилизации частоты колебаний каждого из совокупности данных генераторов.

В каждый момент времени частоты колебаний каждого из генераторов по характеру распределения являются случайными величинами. Совместное распределение случайных величин , представляющих собой векторы размерности , определяется плотностью вероятности с помощью следующего соотношения

, (1)

в котором корреляционная матрица данной векторной случайной величины имеет вид

(2)

Элементами вектора являются отклонения частот в каждом из генераторов от номинальных значений.

В силу того что данные генераторы работают независимо, а отклонения частот каждого из них определяются большим числом независимых факторов, можно считать, что отклонения частот каждого из генераторов от номинального значения определяются нормальным законом распределения, а изменения частоты каждого из генераторов описывается гауссовской случайной последовательностью. При этом в большинстве практических случаев можно считать, что значения отклонений частот каждого из генераторов в различные моменты времени являются независимыми и, соответственно, как показано в [8–15], некоррелированными.

С учетом сделанных предположений можно считать, что матрица является диагональной. В этом случае представление плотности вероятности для распределения случайных значений отклонений частот принимает вид

(3)

Таким образом, можно считать, что отклонения частот каждого из генераторов от номинального значения определяются нормальным законом распределения с нулевым математическим ожиданием и дисперсией, величина которой определяется параметрами и типом генератора и является известной или может быть определена.

Генераторы, имеющиеся в составе одной или группы различных радиоэлектронных систем, образуют собой совокупность одновременно функционирующих генераторов с известными значениями номинальных частот и известными относительными нестабильностями . Отклонения частот каждого из генераторов от номинального значения определяются нормальным законом распределения с нулевым математическим ожиданием и известной дисперсией.

Таким образом, задача заключается в разработке научно-методического аппарата, реализующего статистический метод оценки отклонений частот колебаний генераторов от номинальных значений и формирования управляющих воздействий, позволяющих стабилизировать частоты независимо функционирующих генераторов на основе измерения уходов их фаз от своих номинальных значений.

Рассмотрим систему из генераторов, соединенных как показано на рис. 1. Формируемые каждым генератором сигналы подаются не только на функциональные элементы, определяемые назначением устройств и систем телекоммуникаций, но и дополнительно поступают на вход измерительного устройства И.

Один из генераторов данной совокупности, который в дальнейшем обозначается как _>>, задает временной интервал измерений с номинальной длительностью . При этом к стабильности данного генератора не предъявляются более высокие требования по сравнению с остальными генераторами из рассматриваемой совокупности. Будем считать, что данный временной интервал измерений реализуется при поступлении от _>> генератора определенного количества импульсов или периодов колебаний. В силу отклонения частоты -го генератора от номинального значения длительность временного интервала измерений отличается от номинальной и составляет величину .

Рис. 1 - Блок-схема из k+1 генераторов

Для каждого из данной совокупности генераторов одновременно, в течение одного и того же интервала измерений длительностью с использованием измерителя И определяется полная фаза колебаний, формируемых этими генераторами. Значения фаз колебаний генераторов определяются соотношениями

. (4)

В соотношении (4) – частота k-го генератора на интервале измерений длительностью .

В том случае, когда длительность временного интервала измерений реализуется с погрешностью, много меньшей отклонений частот генераторов от номинальных значений, получение оценок отклонений данных частот не встречает принципиальных сложностей. Однако из-за влияния различных дестабилизирующих факторов и шумов не только частоты колебаний всех генераторов, но и частота выходного сигнала генератора отличается от номинального значения на величину и представляет собой случайную функцию времени. Вследствие этого, как отмечалось выше, длительность временного интервала измерений , задаваемого _>> генератором, реализуется с некоторой погрешностью и составляет величину . При этом величины отклонений частот волновых полей и генератора, задающего интервал измерений, являются соизмеримыми.

С учетом вышесказанного, выражение для фазы колебаний каждого из совокупности генераторов можно представить в следующем виде

,(5)

где ,…,  составляющие отклонения фаз измеренных колебаний от номинального значения для k-го генератора, обусловленные только нестабильностью временного интервала; – составляющие отклонения фаз измеренных колебаний от номинального значения для k-го генератора, обусловленные только нестабильностью собственных частот генераторов; – составляющие отклонений фаз колебаний генераторов, обусловленные нестабильностью как собственных частот генераторов, так и нестабильностью временного интервала одновременно. Однако из-за существенной малости значений последними составляющими можно пренебречь по сравнению с остальными слагаемыми.

С учетом сделанного замечания перепишем выражения (5) в виде

,(6)

где – номинальное значение фазы k-го генератора; – отклонение фазы k-го генератора от номинального значения вследствие собственной нестабильности частоты; – отклонение фазы k-го генератора от номинального значения вследствие нестабильности длительности временного интервала.

Соотношение (6) показывает, что отклонения фаз сигналов, соответствующих каждому из волновых полей, содержат две составляющие и . При этом для каждого из генераторов данные составляющие отклонения фазы колебаний от номинальных значений являются принципиально неразделимыми.

Важным следствием преобразования при переходе от соотношения (5) к (6) является линеаризация уравнений наблюдения, что будет использовано в дальнейшем.

Для решения задачи стабилизации необходимо, прежде всего, разделить составляющие отклонений фаз колебаний генераторов от номинальных значений. Для этого для каждого из совокупности генераторов выразим данные отклонения фаз колебаний, формируемых за интервал времени , следующим образом

.(7)

При этом значения фазы , как отмечалось ранее, являются измеряемыми, а величины – априорно известными .

Подстановка выражения (4) в (7) позволяет получить следующие равенства

.(8)

Составляющие , , …, , как отмечалось выше, не могут быть разделены по результатам измерений, так как в каждой из них содержатся неизвестные величины:

 отклонение длительности временного интервала от номинального значения;  собственные отклонения частот от номинальных значений формируемых колебаний каждого из генераторов.

Каждая из этих величин является неизвестной, но их сумма, равная , определяется с помощью измерительного устройства И.

Выразим из (8) величины отклонений фаз генераторов, обусловленных только их собственными нестабильностями в виде:

.(9)

Подстановка уравнений из системы (7) в уравнения из (9) позволяет получить следующую систему уравнений:

. (10)

В соотношениях (10) номинальное значение длительности временного интервала является известным, а значения отклонений фаз колебаний волновых полей определяются по результатам измерений. Неизвестными являются отклонения частот генераторов от номинальных значений и длительности временного интервала измерений .

Для выполнения дальнейших преобразований будем считать, что на интервале измерений величина отклонения частоты от номинального значения является постоянной. Данное предположение является справедливым в подавляющем большинстве практических случаев устройств и систем телекоммуникаций. При этом данное условие позволяет отказаться от использования алгоритмов фильтрации и перейти к более простым алгоритмам оценки. Возникающая в связи с этим допущением методическая ошибка будет оценена ниже.

Перепишем с учетом сделанного допущения выражения из системы (10) в виде:

.(11)

Как отмечалось ранее, случайные величины являются независимыми и имеют известные параметры распределения (математическое ожидание, медиана или дисперсия). В силу этого плотность распределения (1) случайных величин для каждого момента времени может быть записана в виде (3).

С учетом этого можно отметить, что случайные величины являются независимыми и удовлетворяют нормальному закону распределения с математическим ожиданием, равным нулю:

.(12)

Запишем формулу для плотности нормального закона распределения величины :

,(13)

где – относительная нестабильность k-го генератора .

Величины отклонений частот связаны с нестабильностью временного интервала соотношением (8), что позволяет использовать для оценки нестабильности временного интервала метод наибольшего правдоподобия. В соответствии с данным методом составим функцию наибольшего правдоподобия относительно неизвестного значения отклонения длительности временного интервала :

. (14)

После подставки выражения (8) в (14) и получим следующее выражение относительно переменной :

.(15)

После логарифмирования данной функции получаем:

,(16)

или с учетом свойства логарифмической функции

. (17)

В соответствии с методом наибольшего правдоподобия продифференцируем данную функцию, что позволит получить равенство:

. (18)

В качестве оценки нестабильности временного интервала берется такое значение параметра , при котором производная (17) обращается в нуль. Приравняем данное выражение к нулю, что позволяет получить:

. (19)

Выразим из данного выражения оценку отклонения длительности временного интервала измерений от номинального значения :

. (20)

Полученное значение определяет стационарную точку функции (17). Для того чтобы доказать наличие экстремума, с помощью равенства (18) вычислим вторую производную и оценим выполнение второго достаточного условия локального экстремума:

Исходя из того, что вторая производная функции правдоподобия меньше нуля, функция правдоподобия при значении , определяемом (20), действительно достигает максимума.

Соотношение (19) является необходимым условием локального экстремума функции правдоподобия. В то же время исходя из того, что функция (19) относительно аргумента является квадратичной, можно утверждать, что данный экстремум будет глобальным.

Найденная оценка нестабильности временного интервала позволяет вычислить составляющую для каждого генератора и разделить две составляющие и , определяющие соответственно вклад собственной нестабильности k-го генератора и нестабильности временного интервала измерений в измеренное значение .

Для этого значение подставим в формулу (11) и найдем оценки нестабильности частот каждого из совокупности генераторов, получаемые на основе измеренных значений и полученной с использованием выражения (20) оценки нестабильности временного интервала.

Найденные значения позволяют определить отклонения частот генераторов в виде:

.(21)

Полученные оценки позволяют по измеренным значениям числа импульсов или фаз колебаний каждого из совокупности генераторов и их номинальным значениям определить, на какую величину отличается частота каждого генератора от своего номинального значения. Это дает возможность по результатам измерений и последующей обработки формировать управляющие сигналы для уменьшения отклонения частоты каждого из совокупности генераторов от номинальных значений.

Для анализа статистических характеристик оценок отклонения частот генераторов рассмотрим вначале свойства получаемой оценки нестабильности временного интервала. В силу того, что значение может принимать как отрицательные, так и положительные значения, представим выражение для среднего значения оценки нестабильности временного интервала в следующей форме:

.(22)

Так как величины являются детерминированными, усредняются только случайные величины , математические ожидания которых по предположению равны нулю. В соответствии с этим, с учетом свойств математического ожидания получаем:

.(23)

При записи данного равенства было учтено свойство, что

С учетом ранее сделанных предположений об отклонениях частот генераторов получаем, что средние отклонения фаз колебаний генераторов от номинальных значений равны нулю. Таким образом, получаемая оценка является несмещенной.

Исходя из того, что первый начальный момент случайной величины равен нулю, запишем выражение для второго центрального момента (дисперсии):

Выполняя несложные, но громоздкие преобразования, получаем:

.(24)

С учетом того, что отклонения и каждого из генераторов являются некоррелированными, получаем:

.(25)

Выражение (25) позволяет записать следующее равенство:

С учетом этого представление для дисперсии имеет вид

.(26)

Преобразуем данное выражение при условии, что:

Следовательно, окончательное выражение для дисперсии оценки временного интервала имеет вид

.(27)

Рассмотрим частный случай, при котором все генераторы работают на различных частотах и имеют одинаковые относительные нестабильности . Исследуем характеристики распределения отклонений частот генераторов от номинальных значений для данного случая.

Исходя из того, что первый начальный момент случайной величины равен нулю, на основании соотношения (27) запишем выражение для второго центрального момента (дисперсии):

.(28)

.(29)

Таким образом, увеличение числа генераторов приводит к уменьшению дисперсии оценки нестабильности временного интервала.

Рассмотрим еще один частный случай, когда совокупность генераторов имеет не только одинаковые относительные нестабильности , но и работает на одинаковых частотах . В этом случае дисперсия оценки отклонения длительности временного интервала от номинального значения на основе (29) принимает вид

стабилизация частота генератор

.(30)

Таким образом, использование совокупности K идентичных генераторов с одинаковыми относительными нестабильностями позволяет уменьшить в K раз дисперсию оценки отклонения длительности временного интервала от номинального значения. Данный результат имеет хорошо известную аналогию в теории измерений.

Анализ рассмотренных случаев показывает, что наиболее высокая стабильность обеспечивается при идентичных значениях частот и относительных нестабильностей (30) в системе генераторов, которая составляет величину, равную .

Полученные соотношения позволяют определить статистические характеристики оценок отклонений частот генераторов от номинальных значений.

Воспользуемся соотношением (21), на основании которого представим выражение

. (31)

С учетом свойств математического ожидания [8–15] преобразуем зависимость (30) следующим образом

. (32)

Учитывая некоррелированность отклонений частот и отклонений фаз от номинальных значений в различных генераторах, получим следующую зависимость

, (33)

Используем соотношение , которое легко преобразуется к виду . С учетом последней формулы и ранее сделанных предположений о статистических характеристиках отклонений частот генераторов от номинальных значений в различных генераторах зависимость (32) принимает вид

, . (34)

Дисперсии получаемых оценок определяются зависимостью

, .(35)

В частном случае системы генераторов, имеющих одинаковые нестабильности, получаем

.(36)

Таким образом, соотношения (23), (24) и (34), (36) определяют статистические характеристики оценок отклонения длительности временного интервала измерений и частот генераторов от номинальных значений.

В силу того, что полученное значение оценки отклонения длительности временного интервала от номинального значения отличается от истинного значения, использование управляющего воздействия не приводит к полной компенсации отклонения частоты k-го генератора от номинального значения.

Некомпенсированное отклонение частоты k-го генератора определяется как:

, (37)

или с учетом полученной оценки :

. (38)

В силу того, что измеренное отклонение числа импульсов k-го генератора обусловлено как собственной нестабильностью , так и нестабильностью генератора, задающего временной интервал измерений , запишем данное выражение в следующем виде:

Раскроем величины и , что позволит получить равенство:

.(39)

После несложных преобразований окончательно запишем:

. (40)

Исследуем статистические характеристики нескомпенсированного отклонения частоты k-го генератора (математическое ожидание и дисперсию).

Перепишем выражение (40), раскрыв значение оценки отклонения частоты k-го генератора с использованием соотношения (21):

.(41)

Запишем выражение для нахождения математического ожидания некомпенсированного значения отклонения частоты k-го генератора:

, (42)

где учтено, что

и, следовательно, .

Запишем выражение для нахождения дисперсии нескомпенсированного значения отклонения частоты k-го генератора в виде:

.(43)

После выполнения преобразований получаем

. (44)

Соотношение (44) получено с использованием выражения

Такое значение (44) дисперсия нескомпенсированного отклонения частоты k-го генератора принимает лишь в том случае, когда относительные нестабильности и частоты идентичны.

Таким образом, из выражения (44) следует, что дисперсия нескомпенсированного значения частоты k-го генератора в раз меньше дисперсии отклонения частоты k-го генератора при идентичных параметрах используемых генераторов.

Рассмотрим случай, при котором все генераторы работают на различных частотах и имеют одинаковые относительные нестабильности . В силу того, что математическое ожидание нескомпенсированного отклонения частоты k-го генератора, определяемое выражением (43), равно нулю, определим дисперсию нескомпенсированного отклонения частоты k-го генератора для данного случая. Перепишем выражение (43) с учетом заданных исходных данных:

После преобразования данного выражения получим:

(45)

Предположим, что в выражении (45) , и, следовательно, решение данной задачи может быть сведено к частному случаю, рассмотренному выше:

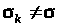
Рассмотрим общий случай, при котором все генераторы работают на различных частотах и имеют отличные друг от друга значения относительных нестабильностей . В силу того, что математическое ожидание значения нескомпенсированного отклонения частоты k-го генератора равно нулю, определим дисперсию нескомпенсированного отклонения частоты k-го генератора для данного случая. Перепишем выражение (43) с учетом заданных исходных данных:

После проведенных преобразований запишем окончательно:

. (46)

Как несложно убедиться, в частном случае идентичных генераторов и решение рассматриваемой задачи сводится к случаю, рассмотренному ранее:

Таким образом, использование совокупности K генераторов позволяет добиться повышения точности оценки отклонений частот генераторов. Потенциальная точность оценивания определяется в общем случае выражением (46). В частном случае идентичных генераторов дисперсия оценки уменьшается в раз.

Выполненные теоретические исследования, определяющие потенциально достижимые значения стабильностей каждого из генераторов, стабилизируемых с использованием рассматриваемого метода и построенного на его основе алгоритма. Для более полного анализа проведем вычислительный эксперимент, позволяющий установить взаимосвязь параметров генераторов и достигаемых значений стабильностей.

Рассмотрим систему из одиннадцати независимых генераторов , работающих на одинаковых частотах с равными относительными нестабильностями. Для численных расчетов использовались следующие исходные данные: номинальные частоты генераторов Гц, относительная нестабильность . Номинальная длительность временного интервала измерений выбиралась равной . Здесь и далее для анализа основных закономерностей рассматривались отклонения как длительности временного интервала, так и частот генераторов от номинальных значений, значения оценок отклонения длительности временного интервала и частот генераторов, а также значения некомпенсированных отклонений частот генераторов от номинальных значений. Данные результаты приведены в табл. 1.

Таблица 1 - Отклонения частот генераторов с одинаковыми значениями нестабильностей

№ генератора	Отклонение длительности интервала измерений от номиналь-ного значения	Оценка отклонения длительности интервала измерений от номиналь-ного значения	Отклонение частоты генератора от номиналь-ного значения	Оценка отклонения частоты генератора от номиналь-ного значения	Нескомпенси-рованное значение отклонения частоты генератора от номиналь-ного значения
1	–3,0617·10–9	–3,3566·10–9	–20,2894	– 23,2386	2,9492
2	–3,0617·10–9	–3,3566·10–9	7,5316	4,5824	2,9492
3	–3,0617·10–9	–3,3566·10–9	–12,8829	–15,8326	2,9492
4	–3,0617·10–9	–3,3566·10–9	–2,6506	–5,5998	2,9492
5	–3,0617·10–9	–3,3566·10–9	12,2459	9,2867	2,9492
6	–3,0617·10–9	–3,3566·10–9	–10,0082	–12,9574	2,9492
7	–3,0617·10–9	–3,3566·10–9	–8,8024	–4,7516	2,9492
8	–3,0617·10–9	–3,3566·10–9	1,5819	–1,3673	2,9492
9	–3,0617·10–9	–3,3566·10–9	–18,2757	–21,2249	2,9492
10	–3,0617·10–9	–3,3566·10–9	–11,6654	–14,6146	2,9492

При проведении исследований рассматривалось сто реализаций, соответствующих различным значениям отклонений частот генераторов от номинальных значений. Номер реализации, для которой приводятся соответствующие результаты, выбирался случайным образом на основании равномерного закона распределений случайных чисел с округлением к ближайшему целому.

Приведенные результаты показывают, что после компенсации в каждой конкретной реализации величина отклонения частоты от номинального значения может возрасти. Это связано с тем, что длина выборки, на основании которой определяется оценка, является конечной, и получаемая оценка отклонения длительности временного интервала измерений от номинального значения не совпадает с истинным значением. При увеличении длины выборки, то есть числа генераторов в системе, расхождение оценки с истинным значением будет уменьшаться. Соответственно, и значения нескомпенсированных отклонений будут уменьшаться.

Перейдем к рассмотрению случая системы из одиннадцати независимых генераторов , работающих на одинаковых частотах с различными относительными нестабильностями. Для численных расчетов использовались следующие исходные данные: номинальные частоты генераторов Гц, относительные нестабильности соответственно , . Номинальная длительность временного интервала измерений выбиралась равной . Результаты исследований приведены в табл. 2.

Полученные результаты показывают, что для данной реализации отклонения частот генераторов от номинальных значений после компенсации значительно уменьшаются. В наибольшей степени это относится к генераторам с более высокой нестабильностью частоты.

Последним этапом исследований данного вопроса является рассмотрение системы из одиннадцати независимых генераторов , работающих на различных частотах с различными относительными нестабильностями. Для численных расчетов использовались следующие исходные данные: номинальные частоты генераторов 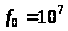Гц, Гц и такими же значениями относительной нестабильности, как и в предыдущем случае. Номинальная длительность временного интервала измерений выбиралась равной . Результаты исследований приведены в табл. 3.

Таблица 2 - Отклонения частот генераторов с различными значениями нестабильностей

№ генератора	Отклонение длительности интервала измерений от номиналь-ного значения	Оценка отклонения длительности интервала измерений от номиналь-ного значения	Отклонение частоты генератора от номиналь-ного значения	Оценка отклонения частоты генератора от номиналь-ного значения	Нескомпенси-рованное значение отклонения частоты генератора от номиналь-ного значения
1	7,1571·10–10	5,7286·10–10	9,1396	10,5691	–1,4285
2	7,1571·10–10	5,7286·10–10	5,4627	6,8912	–1,4285
3	7,1571·10–10	5,7286·10–10	17,9396	19,3621	–1,4285
4	7,1571·10–10	5,7286·10–10	4,5091	5,8155	–1,4285
5	7,1571·10–10	5,7286·10–10	4,3870	5,6945	–1,4285
6	7,1571·10–10	5,7286·10–10	–34,3296	–32,8945	–1,4285
7	7,1571·10–10	5,7286·10–10	101,4612	102,8897	–1,4285
8	7,1571·10–10	5,7286·10–10	–42,5164	–41,0879	–1,4285
9	7,1571·10–10	5,7286·10–10	–76,3188	–74,8904	–1,4285
10	7,1571·10–10	5,7286·10–10	49,2136	50,6421	–1,4285

Таблица 3 - Параметры отклонений в различных реализациях для генераторов при наличии одного высокостабильного генератора

№ генератора	Отклонение длительности интервала измерений от номинального значения	Оценка отклонения длительности интервала измерений от номинального значения	Отклонение частоты генератора от номинального значения	Оценка отклонения частоты генератора от номинального значения	Нескомпенсированное значение отклонения частоты генератора от номинального значения
1	3,031·10^–10	2,9280·10^–10	–10,7289	–12,0320	1,3031
2	3,031·10^–10	2,9280·10^–10	95,6473	93,0412	–2,6061
3	3,031·10^–10	2,9280·10^–10	–9,8169	–13,7261	3,9092
4	3,031·10^–10	2,9280·10^–10	27,4968	–22,2845	5,2123
5	3,031·10^–10	2,9280·10^–10	–55,2055	–61,7210	6,5155
6	3,031·10^–10	2,9280·10^–10	–595,9512	–603,7869	7,8187
7	3,031·10^–10	2,9280·10^–10	–682,9459	–692,0678	9,1219
8	3,031·10^–10	2,9280·10^–10	807,9309	–797,5062	10,4245
9	3,031·10^–10	2,9280·10^–10	26,0213	14,2935	11,7278
10	3,031·10^–10	2,9280·10^–10	212,7528	199,4438	13,0309

Полученные результаты показывают, что и для генераторов, имеющих различные параметры, отклонения частот генераторов от номинальных значений после компенсации значительно уменьшаются. Однако при этом, в отличие от предыдущих случаев, отклонение частоты каждого генератора будет пропорциональным его номинальной частоте.

Таким образом, приведенные результаты моделирования подтверждают основные закономерности, полученные при теоретических исследованиях. Получаемые отличия связаны с ограниченным объемом выборки результатов.

Рассмотрим решение задачи стабилизации частот системы генераторов с использованием предложенного метода для системы, состоящей из генераторов, в следующей постановке: предположим, что -й генератор, задающий временной интервал измерений, является высокостабильным, а к стабильности остальных генераторов не предъявляются высокие требования.

Совокупность генераторов формирует сигналы с номинальными значениями фаз сигналов . Однако на вход измерителя поступают сигналы не с номинальными значениями фаз , а сигналы, фазы которых отличаются на величину , равную сумме двух компонентов:

. (47)

На основании соотношения (27) с учетом условия получаем

. (48)

В случае, если все генераторов имеют одинаковые параметры (относительные нестабильности и частоты), выражение (48) преобразуется к виду

. (49)

Соотношение (49) показывает, что при сделанных допущениях дисперсия оценки отклонения длительности временного интервала от номинального значения определяется стабильностью генератора, задающего длительность временного интервала. При этом для составляющих отклонения фазы от номинального значения k-го генератора можно установить неравенство . В силу данного неравенства следует , что сразу дает возможность получить значение отклонения частоты k-го генератора. Полученный вывод подтверждается данными, приведенными в табл. 4.

Таблица 4 - Параметры отклонений в различных реализациях для генераторов при наличии одного высокостабильного генератора

№ генератора	Отклонение длительности интервала измерений от номинального значения	Оценка отклонения длительности интервала измерений от номинального значения	Отклонение частоты генератора от номинального значения	Оценка отклонения частоты генератора от номинального значения	Нескомпенсированное значение отклонения частоты генератора от номинального значения
1	3,031·10^–10	2,9280·10^–10	–10,7289	–12,0320	1,3031
2	3,031·10^–10	2,9280·10^–10	95,6473	93,0412	–2,6061
3	3,031·10^–10	2,9280·10^–10	–9,8169	–13,7261	3,9092
4	3,031·10^–10	2,9280·10^–10	27,4968	–22,2845	5,2123
5	3,031·10^–10	2,9280·10^–10	–55,2055	–61,7210	6,5155
6	3,031·10^–10	2,9280·10^–10	–595,9512	–603,7869	7,8187
7	3,031·10^–10	2,9280·10^–10	–682,9459	–692,0678	9,1219
8	3,031·10^–10	2,9280·10^–10	807,9309	–797,5062	10,4245
9	3,031·10^–10	2,9280·10^–10	26,0213	14,2935	11,7278
10	3,031·10^–10	2,9280·10^–10	212,7528	199,4438	13,0309

При проведении исследований рассматривался случай, когда стабильность одного из генераторов превышала стабильности каждого из остальных в десять раз, а частоты были одинаковые. В частности, , , а значения частот Гц .

Таким образом, из вышесказанного вытекает утверждение, что метод ФАПЧ может рассматриваться как частный случай предложенного метода стабилизации частот генераторов. При этом генератор, стабильность которого значительно превышает остальные, используется в качестве генератора, задающего временной интервал измерений, то есть выполняет функции опорного генератора как в методе ФАПЧ. Данный вывод подтверждается результатами, приведенными в табл. 4.

выводы

1. Предложенный метод статистической оценки частот генераторов позволяет обеспечивать возможность стабилизации частот системы генераторов в отсутствии высокостабильного эталонного генератора. В основе метода лежит получаемая с использованием метода наибольшего правдоподобия оценка отклонения длительности временного интервала измерений, формируемая на основе одновременной обработки данных об отклонениях фаз колебаний генераторов от их номинальных значений. Найденная оценка дает возможность выделить значения отклонений фаз колебаний генераторов от номинальных значений, обусловленных только их собственными нестабильностями частот. В свою очередь, на основе указанных данных в дальнейшем осуществляется стабилизация генераторов по частоте.

2. С использованием метода наибольшего правдоподобия оценка отклонения длительности временного интервала измерений позволяет определить значение предельно достижимого повышения стабильности частоты каждого из входящих в систему генераторов.

3. Оценки отклонений частот генераторов от номинальных значений являются несмещенными и имеют дисперсию, меньшую, чем дисперсия частоты каждого из генераторов в отдельности.

4. Полученные аналитические соотношения устанавливают взаимосвязь между числом и параметрами стабилизируемых генераторов и предельно достижимыми значениями нестабильностей генераторов при использовании предлагаемого алгоритма. На основе вычислительного эксперимента получены численные оценки предельно достижимой стабильности генераторов при использовании предлагаемого алгоритма.

Выполненное сопоставление разработанного алгоритма статистической стабилизации частот генераторов с методом ФАПЧ показало, что при использовании высокостабильного генератора в качестве генератора, задающего временной интервал измерений, отклонения частот системы генераторов будут обусловлены только собственными нестабильностями и могут быть практически полностью скомпенсированы. Исходя из этого, можно считать, что метод ФАПЧ может рассматриваться как частный случай предлагаемого статистического метода.

Библиографический список

Невдяев Л.М. Персональная спутниковая связь / Л.М. Невдяев, А.А. Смирнов. – М.: Эко-трендз, 2008.

Радиосистемы передачи информации / под ред. И.Б. Федорова и В.В. Калмыкова. – М.: Телеком, 2008.

Катулевский Ю.А. Современные зарубежные тактические радиоустройства / Ю.А. Катулевский // Успехи современной радиоэлектроники. – 2008. – № 3. – Журнал в журнале «Зарубежная радиоэлектроника». – 2008. – № 1.

Тихонов В.И. Статистический анализ и синтез радиотехнических устройств и систем / В.И. Тихонов, В.Н. Харисов. – М.: Радио и связь, 2011.

Крамер Г. Математические методы статистики / Г. Крамер. – М.: Мир, 2008.

Марчук В.И. Первичная обработка результатов измерений при ограниченном объеме априорной информации: монография / В.И. Марчук; под ред. К.Е. Румянцева. – Таганрог: Изд-во ТРТУ, 2007.

Куликов Е.И. Методы измерения случайных процессов / Е.И. Куликов. – М.: Радио и связь, 2006.

Мирский Г.Я. Аппаратурное определение характеристик случайных процессов / Г.Я. Мирский. – М.-Л.: Энергия, 2007.

Салычев О.С. Скалярное оценивание многомерных динамических систем / О.С. Салычев. – М.: Машиностроение, 2007.

Устойчивые статистические методы оценки данных / под ред. Р.Л. Лонера. – М.: Машиностроение, 2009.

Мудров В.И. Методы обработки измерений / В.И. Мудров, В.Л. Кушко. – М.: Сов. радио, 2006.

Гихман И.И. Введение в теорию случайных процессов / И.И. Гихман, А.В. Скороход. – М.: Наука, 2007.

Корн Г. Справочник по математике (для научных работников и инженеров) / Г. Корн, Т. Корн. – М.: Наука, 2008. – 832 с.

Спутниковые системы персональной и подвижной связи для обслуживания абонентов на территории России / под ред. А.А. Кучейко. – М.: ИПРЖР, 2011.