Метод кусочного размножения оценок при обработке реализаций сигналов ограниченного объема

Содержание

1. Обработка реализаций сигналов ограниченного объема

2. структурная схема устройства, реализующая метод кусочного размножения оценок

3. временные и частотные характеристики устройства, реализующего метод кусочного размножения оценок

выводы

Библиографический список

1. Обработка реализаций сигналов ограниченного объема

Существующие методы обработки широко применяются при решении прикладных задач в системах телекоммуникаций, метрологии, статистической обработки. Как правило, их использование определяется начальными условиями: модель взаимодействия полезной и шумовой составляющей; ограничения, накладываемые на компоненты модели обрабатываемого сигнала. Разнообразие методов обработки составляет разнообразие начальных условий, на которых они определены. Начальные условия большинства методов обработки пересекаются и, при решении конкретной задачи, существует возможность использования нескольких различных подходов к получению оценок полезного сигнала. Во многом это связано с тем, что при определении ряда начальных условий накладываются не жесткие ограничения, что образует ряд альтернативных подходов к обработке. В данных ситуациях необходимо решать задачу не только обработки сигнала, но и выбора наиболее приемлемого метода оценивания, что является более сложной задачей. К методу обработки предъявляются требования, которые во многих случаях трудно достичь при использовании только одного алгоритма. В общем случае такими требованиями являются: обработка сигналов, описываемых широким классом функций; эффективное подавление шума, который описывается широким классом случайных функций; простота реализации; возможность эффективно обрабатывать реализации различных объемов в условиях априорной неопределенности о составляющих анализируемого процесса.

Несмотря на противоречивость выдвигаемых требований, в ряде последних работ В.И. Марчука, В.Я. Катковника, К.О. Егиазаряна, Я. Астола предложены новые подходы и методы ослабления шумовой составляющей, позволяющие существенно расширить начальные условия обработки и сделать более мягкими ограничения на свойства составляющих математической модели, описывающей исходную реализацию.

В качестве модели обрабатываемого сигнала наиболее часто используется на практике аддитивная модель, которая определяется выражением:

, (1)

где – неслучайный полезный сигнал, – случайные составляющие, действующие на фоне полезного сигнала. Закон распределения каждой составляющей различен.

Математическая модель полезной составляющей в большинстве случаев является многокомпонентной, что осложняет ее анализ и обработку. В общем случае модель полезного сигнала можно представить элементом множества гладких функций , которое определяется следующим образом [4]:

,

где – максимальный порядок производной функции множества .

Во множестве функций можно выделить подмножество гармонических функций [4]:

,

а также часть пространства составляет подпространство полиномиальных функций:

. (2)

Как правило, на практике рассматривают подмножество , ограниченное условием . Принятое ограничение связано с условием гладкости, заключающееся в том, что любую модель из пространства можно приблизить полиномами невысокой степени на интервале [1].

При построении математической модели случайной (шумовой) составляющей (1) выдвигается предположение о том, что составляющие имеют гауссовский закон распределения с нулевым математическим ожиданием [3]. Как и в случае полезного сигнала, шумовую составляющую в общем случае можно представить элементом множества случайных процессов [2]:

.

В случае представления реализации результатов измерения в виде дискретного ряда выражение (1) запишется в виде [8]:

, . (3)

Таким образом, исходная реализация результатов измерений представляет собой ряд , в котором значения получены в равноотстоящие моменты времени, то есть . Для упрощения дальнейшего анализа полученных результатов измерений произведем нормировку значений относительно времени дискретизации . В результате , а выражение (3) представляется в виде суммы отсчетов дискретных рядов – полезного сигнала и шумовой составляющей:

, . (4)

Отсчеты полезного сигнала принадлежат к пространству . Отсчеты аддитивной шумовой составляющей принадлежат случайному процессу пространства .

Исходная последовательность представляет собой реализацию нестационарного случайного сигнала, математическое ожидание которого является функционально зависимым. Сложность обработки таких реализаций заключается в отсутствии априорных данных о функциональной зависимости математического ожидания [5]. Априорно неизвестна функциональная зависимость полезного сигнала , но предполагается, что она относится к пространству функций (2), шумовая составляющая принадлежит к пространству , а плотность ее распределения симметрична относительно математического ожидания. Наряду с априорной информацией о составляющих обрабатываемого сигнала, немаловажным является объем его реализации. В условиях проведения уникальных экспериментов и невозможности получить достаточных объемов реализаций ограничения на объем выборки являются самыми существенными. В условиях ограниченности объема реализации предполагается, что выборка составляет от 30 до 150 значений [2]. Для получения оценки полезной составляющей сигнала необходимо уменьшить дисперсию шумовой составляющей путем осуществления сглаживания.

Таким образом, при таком определении начальных условий использование большинства существующих методов обработки ограниченно. В первую очередь это связано с зависимостью оптимальных значений их параметров обработки от формы полезной составляющей и закона распределения шума [2]. В большинстве случаев при такой постановке задачи производится сглаживание реализации простыми методами: простое скользящее среднее, взвешенное скользящее среднее, медианное сглаживание, экспоненциальное сглаживание и т.д. [1]. Следует отметить, что их использование на выборках ограниченного объема обладает существенными недостатками [3]. Решение задачи выделения полезной составляющей осуществляется методом наименьших квадратов с использованием наиболее подходящей аппроксимирующей функции в смысле определенного критерия. При этом оптимальный выбор аппроксимирующей функции крайне затруднителен в условиях априорной неопределенности. В работах Дж. Бендата и А. Пирсона, С.М. Переверткина и ряда других указывается на то, что наилучшее оценивание полезного сигнала достигается, когда исходный сигнал представлен ансамблем реализаций, а оценка полезного сигнала осуществляется путем их усреднения по сечениям. В связи с этим предлагается использовать метод выделения полезного сигнала (патент № 2257610), основанный на разбиении исходной реализации на перекрывающиеся интервалы одинаковой длины, с последующей оценкой на каждом из них полезного сигнала методом наименьших квадратов с полиномиальной аппроксимирующей функцией. Такой подход позволяет получить множество оценок полезного сигнала в каждом сечении процесса с последующим их усреднением [1].

Согласно выражению (4) исходная выборка представляет собой последовательность отсчетов . Для получения оценки полезной составляющей разбиваем исходную реализацию на перекрывающихся интервалов, как показано на рис. 1. Длина каждого интервала фиксирована и равна априорно заданной величине . Разбиение формируется таким образом, что отсчетов предыдущего интервала содержится в последующем интервале. Данный способ разбиения позволяет сохранить корреляционные связи между отсчетами при последующем получении оценок полезного сигнала. Исходная последовательность с учетом предлагаемого разбиения перепишется в следующем виде , где [9].

Исходный ряд , можно представить в виде матрицы размера :

. (5)

На каждом скользящем интервале производится оценка полезной составляющей (рис. 1). Как показано на рис. 1, полученные оценки группируются (группы оценок обведены овалами). Результирующая оценка получается путем усреднения множества оценок полезного сигнала, полученных в результате аппроксимации. На основе анализа предлагаемого разбиения исходной реализации выделим три участка:

,,.

Рис. 1. Пример разбиения исходной реализации сигнала на перекрывающиеся интервалы постоянной длины

Выделение трех участков связано с тем, что в начале и конце реализации оценивание происходит по группам оценок различного объема. На первом интервале исходной выборки , количество оценок полезной составляющей в каждый момент времени пропорционально номеру отсчета , на втором интервале – количество оценок равно ширине скользящего интервала и составляет значение, а на последнем интервале оценивания , с ростом номера отсчета количество оценок в каждом сечении уменьшается от до 1 (рис. 1).

Оценка исходного ряда (5) представляет собой также матрицу такого же размера :

. (6)

Матрица (6) получается в результате оценивания полезной составляющей по значениям , , каждой строчки матрицы (5). Для перехода от матричного представления оценки обратно к одномерной реализации необходимо усреднить ее значения по столбцам. Результирующая оценка полезной составляющей запишется в следующем виде:

(7)

Значения оценок, составляющие матрицу (6), получены путем аппроксимации исходной реализации , для каждого методом наименьших квадратов. Таким образом, соответствует номеру строки матрицы оценок (6). В работе [9] приведены результаты исследования для случая, когда на каждом интервале производится аппроксимация функциями пространства (2), при этом оно ограничено условием . Полученные результаты являются частными и не позволяют исследовать зависимость погрешности оценивания от параметров метода обработки. Для проведения таких исследований необходимо получить общее решение задачи аппроксимации на каждом скользящем участке для аппроксимирующего полинома произвольной степени . Использование ранее предложенного подхода имеет следующие недостатки [5]:

    минимизация целевой функции метода наименьших квадратов при произвольной степени аппроксимирующего полинома сводится к решению системы уравнения, что приводит к значительным вычислительным затратам при больших ;

    в случае, если необходимо увеличить или уменьшить степень аппроксимирующего полинома, производится полный пересчет всех ранее полученных коэффициентов и оценок.

Использование системы ортогональных многочленов позволяет устранить эти недостатки.

Исходная дискретная последовательность определена в узле. Введем систему ортогональных многочленов Лежандра, где последовательно возрастающих степеней, обладающие свойством [5]:

,

где – некоторая весовая функция. Будем рассматривать случай, когда .

Таким образом, имея систему ортогональных многочленов, можно построить многочлен наилучшего приближения в смысле минимума квадратичной целевой функции. В общем случае аппроксимирующую полиномиальную функцию можно представить в виде [5]:

. (8)

Отметим, что полином (8) также принадлежит к пространству (2).

В соответствии с общей теорией ортогональных многочленов коэффициенты определяются выражением [5]:

, (9)

где – норма ортогональных многочленов.

В соответствии с предлагаемым методом разбиения оценки коэффициентов полинома (8) на каждом скользящем интервале различны, тогда выражение (9) перепишется в следующем виде:

,

где , – длина интервала разбиения.

Анализ выражения для показывает, что коэффициенты зависят не только от степени полинома, но и от номера интервала . В соответствии с выражением (7) результирующая оценка полезного сигнала через системы ортогональных многочленов запишется в следующем виде:

кусочное размножение оценка сигнал

(10)

где индекс в показывает степень аппроксимирующего полинома на каждом скользящем интервале.

Выражение (10) представляет собой обобщенное уравнение, которое позволяет получить оценку полезной составляющей предлагаемым способом разбиения с последующей аппроксимацией на каждом скользящем интервале полиномом произвольной степени . Так как пространство аппроксимирующих функций (2) ограничено условием , то на основе выражения (10) можно получить частные случаи при , и [9].

В случае, когда , выражение (10) запишется в следующем виде:

(11)

При выражение (10) имеет вид:

(12)

При выражение (10) имеет вид:

(13)

Выражения (11)–(13) эквивалентны ранее полученным выражениям в работе [2]. В отличие от выражений, полученных на основе неортогональных полиномов [2], использование выражения (10) позволяет увеличить степень аппроксимирующего полинома без пересчета ранее полученных оценок. Анализ выражений (12) и (13) показывает, что степень аппроксимирующего полинома может быть увеличена путем вычисления дополнительных членов суммы. Такое свойство (10) позволяет модифицировать предлагаемый способ оценивания. Обладая дополнительной информацией о выделяемом полезном сигнале на локальном участке обработки, можно увеличивать или уменьшать степень аппроксимирующего полинома, тем самым ввести элементы адаптации.

На рис. 2 представлен пример разбиения исходной реализации на перекрывающиеся интервалы одинаковой длины и аппроксимации на каждом из функцией пространства (2) при , при этом модель исходной реализации представляет собой функцию этого же пространства с .

Рис. 2. Пример разбиения исходной реализации на пересекающиеся интервалы постоянной длины и аппроксимации на каждом из них значений сигнала линейной функцией

На рис. 3 представлены результаты вычисления оценки сигнала на основе выражения (12). Кривая 1 представляет собой исходный сигнал, а кривая 2 – его оценку. Множество оценок полезного сигнала, полученные в каждый момент , представлены крестиками (рис. 3). На основе их значений в соответствии с выражением (12) получаем оценку полезной составляющей (кривая 2). Несовпадение исходной реализации с оценкой полезной составляющей на начальном участке реализации объясняется тем, что количество оценок полезной составляющей в каждый момент является неодинаковым и увеличивается до момента . При количество оценок постоянно и равно длине выбранного ранее окна , а ошибка оценки полезного сигнала меньше, чем .

Рис. 3. Пример получения множества оценок полезного сигнала в каждом сечении исходного процесса (1) и формировании на их основе результирующей оценки (2) при отсутствии аддитивной шумовой составляющей

На рис. 2 и 3 представлена только часть реализации. Для третьего интервала оценивания результат оценки схож с первым интервалом .

Недостатком предлагаемого метода обработки является то, что для первых и последних значений исходной реализации множество оценок содержит различное количество элементов (рис. 1). Следствием этого является увеличение ошибки оценки полезной составляющей на интервалах и (рис. 3). Для уменьшения погрешности оценки полезной составляющей на интервалах и предлагается модифицировать разбиение исходной реализации на этих интервалах. Для этого вводится дополнительный параметр , который имеет смысл минимальной длины окна разбиения.

Для осуществления разбиения исходной реализации задается значение и , при этом необходимо, чтобы выполнялось условие . На начальном интервале исходная реализация разбивается на перекрывающиеся интервалы с фиксированной левой границей и нарастающей длиной интервала разбиения от до , как показано на рис. 4.

Рис. 4. Пример модифицированного разбиения исходной реализации на перекрывающиеся интервалы с изменяющейся длиной интервала разбиения в начале и конце выборки

На интервале разбиение исходной реализации осуществляется с уменьшением длины интервалов до минимального значения с фиксированной правой границей (рис. 4).

Обозначим минимальную длину интервала через . Используя модифицированный подход разбиения исходного ряда, матрица (5) перепишется в следующем виде:

. (14)

Использование разбиения, представленного на рис. 4, позволяет получить на интервалах и дополнительные оценки полезной составляющей и тем самым уменьшить ее погрешность.

При проведении аппроксимации на каждом интервале полиномом степени выражение (10) для вычисления результирующих оценок запишется в следующем виде:

(15)

На рис. 5 представлен пример обработки реализации модифицированным методом кусочного размножения оценок полезной составляющей. Представлена часть реализации для интервала .

Анализ рис. 5 показывает, что использование модифицированного подхода разбиения позволяет увеличить количество оценок на граничных интервалах и . Сравнительный анализ результатов, представленных на рис. 3 и 5, показывает, что в случае использования модифицированного алгоритма оценки полезной составляющей ее значения более близко расположены к значениям исходного сигнала, чем для случая немодифицированного подхода.

Рис. 5. Пример получения множества оценок полезного сигнала в каждом сечении исходного сигнала (1) и формирование на их основе результирующей оценки (2) при использовании модифицированного подхода разбиения исходной реализации на перекрывающиеся интервалы и отсутствии аддитивной шумовой составляющей

Предлагаемый метод обработки, несмотря на некоторую сложность представленных выражений, легко реализуется на современной элементной базе. Основу оценивания полезной составляющей на каждом элементарном интервале составляет метод наименьших квадратов с полиномиальной аппроксимирующей функцией. Условие обязательной полиномиальной аппроксимации на каждом участке является нежестким. Аппроксимация может быть произведена любой функцией из пространства (2). Так как интервал разбиения исходной выборки фиксирован, а также фиксирована аппроксимирующая функция в процессе обработки, это позволяет получить выражение оператора предлагаемого метода обработки.

2. структурная схема устройства, реализующая метод кусочного размножения оценок

Следует отметить, что предлагаемый метод обработки является симбиозом метода скользящего среднего и метода размножения оценок [3]. Используя выводы, при получении оценки полезного сигнала методом скользящего среднего, структурная схема устройства, его реализующая, показана на рис. 6. Устройство содержит буферный блок, блок аппроксимации, блок оценки и блок управления. Устройство, реализующее метод скользящего среднего, реализуется последовательной схемой. Исходная реализация поступает в буферный блок, где записываются первые значения . С буферного блока последние значения передаются в блок аппроксимации, где осуществляется их аппроксимация полиномиальной функцией, используя метод наименьших квадратов. Аппроксимирующей функцией является полином степени пространства (2). В блоке оценок осуществляется вычисление оценки полезного сигнала путем вычисления значения аппроксимирующего полинома в центральной точке интервала аппроксимации, что соответствует процедуре нахождения оценки методом простого скользящего среднего. Результирующая оценка поступает на выход устройства (рис. 6).

Рис. 6. Структурная схема устройства, реализующая метод скользящего среднего

С помощью блока управления задаются параметры обработки: длина скользящего интервала (ширина скользящего окна) и степень аппроксимирующего полинома . В случае, когда или , оценка на выходе устройства эквивалентна использованию метода простого скользящего среднего, а при или – методу взвешенного скользящего среднего.

На рис. 7 представлена структурная схема устройства, реализующего метод кусочного размножения оценок (10). Устройство представляет собой набор из каналов, каждый из которых содержит в себе блок задержки, буферный блок, блок аппроксимации, сумматор. Параметры обработки задаются с помощью блока управления. Значения исходной реализации через блоки задержки записываются в буферные блоки каждого из каналов.

Рис. 7. Структурная схема устройства, реализующего метод кусочного размножения оценок

Все блоки задержки устройства являются идентичными и позволяют создавать задержку на один такт работы устройства. В каждом канале содержатся значения исходной реализации в m отсчетов, сдвинутые относительно друг друга на один такт, что соответствует используемому способу разбиения исходной реализации (рис. 1). Значения обрабатываемой реализации с буферных блоков поступают в блоки аппроксимации, где осуществляется их аппроксимация с помощью метода наименьших квадратов, используя полиномиальную аппроксимирующую функцию степени (рис. 7). В блоках аппроксимации вычисляются значения аппроксимирующих функции и производится их взвешивание (7). Значения аппроксимирующих функций через блоки задержки поступают на сумматоры (рис. 7). На выходе устройства формируется оценка полезного сигнала. С помощью блока управления определяется число каналов обработки; размер каждого буфера канала, который равен длине интервала разбиения реализации ; степень аппроксимирующего полинома в блоках аппроксимации. В случае , и – оценки на выходе устройства описываются выражениями (11), (12) и (13) соответственно. Структурная схема устройства, представленная на рис. 1, является одним из прототипов устройства, реализующего метод кусочного размножения оценок (рис. 7). В отличие от метода размножения оценок, интервал разбиения исходной реализации фиксирован, а оценку полезного сигнала можно получать по мере поступления данных. Структурная схема устройства, представленная на рис. 6, также является прототипом устройства, реализующего метод кусочного размножения оценок (рис. 7), но при всей схожести используется оценка полезного сигнала, полученного на всем интервале (10), в отличие от метода скользящего среднего, где она вычисляется только в его середине.

Приведенная структурная схема реализации устройства на основе метода кусочного размножения оценок является одним из вариантов. В каждом конкретном случае и в зависимости от используемого оборудования структурная схема может модифицироваться. Возможность распараллеливания вычислений при реализации метода кусочного размножения оценок позволяет реализовывать его на базе многопроцессорных систем.

В результате при реализации предлагаемого метода кусочного размножения оценок полезного сигнала устройство представляет собой дискретный фильтр, а использование непосредственного вычисления коэффициентов аппроксимирующего полинома и получение оценок на каждом интервале разбиения, с последующим усреднением их по полученным множествам, с вычислительной точки зрения не выгодно. Как правило, стационарная система характеризуется откликом на единичное воздействие. В связи с этим представляет интерес получить выражения отклика системы, который зависит от параметров метода кусочного размножения оценок (размер скользящего окна , степень аппроксимирующей функции ).

3. временные и частотные характеристики устройства, реализующего метод кусочного размножения оценок

В общем случае выражение (10) можно рассматривать как уравнение дискретного фильтра. Рассмотрим предлагаемый метод оценивания с точки зрения реализации его в виде дискретного фильтра и получим его системную функцию [3].

В общем виде системная функция линейного стационарного дискретного фильтра представляет собой отношение -преобразования выходного сигнала к -преобразованию входного сигнала [3, 4]. Сопоставим дискретным сигналам , и импульсной характеристике дискретного фильтра соответственно их Z-преобразования , и . Так как выходной сигнал является сверткой входного сигнала с импульсной характеристикой устройства, то можно записать [3, 4]:

. (16)

Таким образом, чтобы определить системную функцию дискретного фильтра (16), необходимо определить его импульсную характеристику, которая является откликом системы на единичное воздействие.

В этом случае функция единичного скачка, подаваемого на вход, описывается выражением [1]:

, , (17)

где переменная определяет положение единичного импульса в исходной выборке, подаваемой на вход.

В случае стационарной системы ее отклик не зависит от [3]. Отметим, что рассматриваемый метод имеет особенности, связанные с тем, что способы оценивания на интервалах исходной выборки , и различны. Таким образом, введем начальные условия, которые заключаются в определении отклика системы на интервале .

В этом случае функция единичного скачка (17), подаваемого на вход, перепишется в следующем виде:

,. (18)

Используя выражение (5) и определение исходного сигнала (14), запишем отклик системы, описываемой выражением (6):

, (19)

где индекс в показывает степень аппроксимирующего полинома.

Анализ выражения (10) показывает, что отклик системы является четной функцией относительно , тогда выражение (19) для интервала 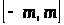перепишется следующим образом:

. (20)

На рис. 8 представлен график функции , при различных значениях параметра . Так как пространство аппроксимирующих функций (2) ограничено условием , то представлены графики функции при , и [9]. Зависимости, показанные на рис. 8, получены при фиксированном значении ширины интервала разбиения . Анализ результатов, представленных на рис. 8, показывает, что полученные импульсные характеристики фильтра имеют затухающий характер. Отклик системы на единичное воздействие при имеет треугольную форму, с ростом значения , характеристика принимает затухающий характер и колеблется относительно нуля. Число колебаний импульсной характеристики пропорционально параметру . Импульсная характеристика по модулю не превосходит некоторой постоянной величины, что позволяет сделать вывод об устойчивости анализируемого фильтра [3, 4].

Рис. Импульсная характеристика дискретного фильтра, реализующего метод кусочного размножения оценок при различных степенях аппроксимирующего полинома на каждом интервале разбиения

Длина импульсной характеристики определяется параметром и является четной функцией относительно . Таким образом, дискретный фильтр представляет собой КИХ фильтр (дискретный фильтр с конечной импульсной характеристикой) с симметричной импульсной характеристикой [17]. Анализ выражения (20) показывает, что форма импульсной характеристики для каждого определяется и пропорциональна ее автокорреляционной функции.

В соответствии с выражением (16) системной функцией дискретного фильтра является -преобразование импульсной характеристики [3, 17]. Произведя -преобразование импульсной характеристики (20), получим выражение для системной функции дискретного фильтра :

(21)

где индекс показывает степень аппроксимирующего полинома.

Заменяя в (21) на , получим выражение для частотного коэффициента передачи цифрового фильтра .

На рис. 9 представлены результаты расчета модуля частотного коэффициента передачи дискретного фильтра (амплитудно-частотные характеристики – АЧХ), полученные выражением (21).

Рис. 9. Амплитудно-частотная характеристика дискретного фильтра, реализующего метод кусочного размножения оценок при длине интервала разбиения и различной фиксированной степени аппроксимирующего полинома на каждом интервале

Так как частотная характеристика является периодической функцией частоты с периодом, равным частоте дискретизации, то используется нормировка для проведения сравнений характеристик различных фильтров. Ось частот рис. 9 нормирована относительно , и вся характеристика находится в интервале . А так как характеристика симметрична относительно , то на рис. 9 и далее рассматривается интервал [3].

Анализ результатов, представленных на рис. 9, показывает, что АЧХ дискретного фильтра зависит от степени аппроксимирующего полинома . Максимальный уровень боковых лепестков составляет -24 дБ при , -17 дБ при и -11 дБ при . Максимальный уровень боковых лепестков практически линейно увеличивается с ростом [2]. Для сравнения АЧХ различных оконных функций вводят понятие эквивалентной шумовой полосы, которая определяется следующим образом [3]:

. (22)

Если исходная обрабатываемая последовательность представляет собой сумму гармонического сигнала с частотой, кратной частоте ДПФ и белого шума, тогда значение показывает, во сколько раз уменьшается отношение сигнал-помеха после обработки входной последовательности оконной функцией. Таким образом, используя выражение (21) и (22), значение эквивалентной шумовой полосы составит при – , при – и при – . С ростом степени аппроксимирующего полинома полоса пропускания дискретного фильтра увеличивается по линейному закону.

Расширение полосы пропускания при увеличении степени аппроксимирующего полинома связано с тем, что происходит выделение не только низкочастотной составляющей, но и учитываются колебательные процессы более высокой частоты. В случае выбора степени полинома, равной , будут учтены все составляющие спектра входного сигнала, и выходной сигнал полностью повторит входной.

На рис. 10 представлены графики расчета фазочастотной характеристики коэффициента передачи фильтра (ФЧХ) (21).

Рис. 10. Фазочастотная характеристика дискретного фильтра, реализующего метод кусочного размножения оценок при длине интервала разбиения и различной степени аппроксимирующего полинома на каждом интервале

Анализ результатов, представленных на рис. 10, показывает, что фазочастотные характеристики имеют колебательный характер и асимптотически затухают. При этом колебания тем быстрее затухают, чем меньше степень . С уменьшением степени аппроксимирующего полинома и увеличением частоты амплитуда колебаний фазы уменьшается, приближаясь к нулю в полосе прозрачности фильтра.

На рис. 11 представлены АЧХ дискретного фильтра, для сравнения, при и . Анализ рис. 11 показывает, что с увеличением значение параметра в два раза привело к уменьшению абсолютной полосы пропускания фильтра во столько же раз. При этом эквивалентная шумовая полоса не изменится, так как является относительной к длине импульсной характеристики , длина которой определяется параметром (22).

Рис. 11. Семейство амплитудно-частотных характеристик дискретного фильтра, реализующего метод кусочного размножения оценок при длине интервала разбиения , и различной степени аппроксимирующего полинома на каждом интервале

Увеличение в два раза несколько уменьшило максимальный уровень боковых лепестков, который составил -26 дБ при , -20 дБ при и -16,6 дБ при . Также одним из показателей сравнения различных дискретных фильтров является ширина главного лепестка АЧХ на уровне дБ и дБ, отнесенная к длине импульсной характеристики.

Для анализируемого фильтра ширина главного лепестка составила и при ; и при ; и при . Проводя сравнения с аналогичными характеристиками для различных оконных функций, приведенных в работах Рабинера и Гоулда, Гольденберга, Хариса [3, 17, 19], отметим следующее: характеристики анализируемого дискретного фильтра при полностью совпадают с характеристиками оконной функции треугольной формы. Полученный результат закономерен, так как отклик дискретного фильтра при имеет такую же форму (рис. 8). С ростом степени аппроксимирующего полинома происходит увеличение ширины главного лепестка АЧХ фильтра по уровню 3 и 6 дБ, при этом также расширяется эквивалентная шумовая полоса . Ширина главного лепестка не зависит от параметра сглаживания , а определяет только длину импульсной характеристики фильтра и, как следствие, его разрешающую способность в частотной области [7, 16].

На рис. 12 представлен график ФЧХ для сравнения при и и различных степенях аппроксимирующего полинома .

Рис. 12. Семейство фазочастотных характеристик дискретного фильтра, реализующего метод кусочного размножения оценок при длине интервала разбиения , и различной фиксированной степени аппроксимирующего полинома на каждом интервале

Анализ характеристики, представленных на рис. 12, позволяет сделать вывод, что форма ФЧХ не зависит от параметра . Таким образом, увеличение значения параметра не привело к эквивалентному изменению формы характеристики, а только изменило масштаб зависимости [9].

При анализе дискретного фильтра, который описывается уравнением (10), рассматривается случай, когда функция единичного скачка (17) определена на интервале , хотя исходное уравнение определено на интервале . Это связано с тем, что способ оценивания на интервалах выборки , и различен, но при этом на интервале существует симметрия в подходе оценивания. В общем случае дискретный фильтр, описываемый уравнением (6), является нестационарным, а отклик системы на интервалах и зависит от положения единичного скачка (17).

Используя выражение (9) и определение исходного сигнала (17), запишем отклик системы, описываемой выражением (10):

(23)

Выражение (23) представляет собой отклик системы в случае, когда исходная последовательность ограничена интервалом и обрабатывается с помощью предлагаемого метода кусочного размножения оценок с учетом особенностей на интервалах и . При этом отметим, что выражение для отклика системы при (23) полностью эквивалентно ранее полученному выражению для (20) и не зависит от (17).

На рис. 13 представлено семейство откликов дискретной системы, которая описывается выражением (23) для интервала и . Отметим, что для характер зависимости эквивалентен. Анализ рис. 13 показывает, что с увеличением отклик системы переходит от антисимметричной зависимости к симметричной зависимости, при этом большему изменению подвергается левая часть импульсной характеристики, чем правая относительно ее максимума. При форма импульсной характеристики становится постоянной и не зависит от .

Рис. 13. Семейство импульсных характеристик дискретной системы, реализующей метод кусочного размножения при получении оценки полезного сигнала на начальном интервале значений при параметре

На рис. 14 представлено семейство АЧХ, полученных на основе семейства характеристик, представленных на рис. 13 при .

Рис. 14. Семейство амплитудно-частотных характеристик дискретной системы, реализующей метод кусочного размножения при получении оценки полезного сигнала на начальном интервале значений при параметре

На рис. 14 представлено семейство АЧХ при различных значениях . Анализ результатов, приведенных на рис. 13 и 14, показывает, что оценка полезного сигнала на интервалах и является нелинейной и представляет собой прохождение исходной реализации через набор фильтров с различными АЧХ. Результаты, представленные на рис. 14 и 13, следует интерпретировать следующим образом. Каждый отсчет на интервале и получен в результате свертки исходной реализации с соответствующей импульсной характеристикой (рис. 13), то есть выбор импульсной характеристики на интервале и для вычисления оценки полезного сигнала определяет значение (23). С точки зрения АЧХ, оценкам полезной составляющей, имеющим большую погрешность, соответствуют фильтры с большей полосой пропускания, то есть большее число спектральных составляющих как полезного сигнала, так и шума участвуют в ее получении. С ростом полоса фильтров уменьшается и стремится к АЧХ для стационарного случая (21) при (рис. 14). На основе полученных результатов устройство, реализующее метод кусочного размножения оценок, можно представить в виде банка фильтров с различными АЧХ. Если зафиксировать объем выборки, то для граничных интервалов оценивания и характеристики фильтров будут иметь вид, представленный на рис. 14.

Таким образом, аналитически показано, что обработку методом кусочного размножения оценок можно рассматривать с точки зрения дискретной фильтрации. Параметры метода обработки однозначно связаны с системной функцией фильтра. Получены выражения для нахождения импульсной характеристики дискретного фильтра, которая зависит как от параметра и степени аппроксимирующего полинома на каждом интервале (20). Исследования показывают, что с ростом происходит расширение эквивалентной шумовой полосы и эквивалентной ширины главного лепестка АЧХ. Максимальный уровень ослабления помехи достигается при условии . Отметим, что этот параметр фильтра имеет смысл рассматривать с точки зрения максимизации отношения сигнал/помеха. Этот критерий не учитывает формы полезной составляющей, так как отдельные спектральные составляющие полезного сигнала могут находиться вне полосы пропускания фильтра, что приведет к искажению оценки и, как следствие, к росту погрешности. Увеличение степени аппроксимирующего полинома на каждом скользящем интервале приводит к увеличению ширины полосы пропускания фильтра и максимального уровня боковых лепестков, однако при этом удается получить оценку с меньшей погрешностью. Существует некоторое противоречие, которое заключается в том, что, повышая гладкость получаемой оценки, приходится расширять полосу пропускания фильтра и ослаблять его фильтрующие свойства в силу роста максимального уровня боковых лепестков.

Использование разработанного дискретного фильтра позволяет существенно упростить реализацию метода обработки в виде устройства на базе цифровых сигнальных процессоров различного класса.

выводы

    Разработан метод кусочного размножения оценки полезного сигнала (патент № 2257610), позволяющий обрабатывать исходную реализацию ограниченного объема в условиях априорной неопределенности о полезном сигнале и аддитивной шумовой составляющей.

    Получены выражения, устанавливающие связь между значениями исходной реализации и значениями оценки полезного сигнала при произвольной степени аппроксимирующего полинома и значении , используя систему ортогональных полиномов. Использование свойств ортогональных многочленов имеет широкие возможности для модификации предлагаемого метода обработки, адаптируя степень аппроксимирующей функции на каждом отдельном скользящем интервале.

    Рассмотрена возможность уменьшения погрешности оценки полезного сигнала на начальном и конечном интервале исходной выборки путем модификации метода кусочного размножения, основанной на дополнительном разбиении исходной реализации на этих интервалах, позволяющая увеличить число оценок полезного сигнала в сечениях исходного процесса.

    Получены выражения для импульсной характеристики и системной функции устройства, реализующего принцип обработки методом кусочного размножения оценок, которые зависят от параметров обработки. Рассмотрен как стационарный, так и нестационарный случай.

    Исследования системной функции дискретного фильтра, реализующего метод кусочного размножения оценок, показали, что степень аппроксимирующего полинома на каждом интервале и ширина интервала разбиения однозначно определяют параметры амплитудно-частотной и фазочастотной характеристики устройства. Максимальный уровень боковых лепестков амплитудно-частотной характеристики слабо зависит от и в среднем составляет -25 дБ при , -18 дБ при и -13 дБ при . Ширина главного лепестка не зависит от параметра и составляет при – , при – и при – .

    Проведены исследования особенности изменения характеристик дискретной системы при реализации обработки на начальном и конечном интервале исходной выборки сигнала.

Библиографический список

      Адаптивные фильтры / под ред. К.Ф.Н. Коуэна и П.М. Гранта. – М. : Мир. – 200

      Бендат, Дж. Прикладной анализ случайных данных ; пер. с англ. / Дж. Бендат, А. Пирсол. – М. : Мир, 2009. – 540 с.

      Гольденберг, Л.М. Цифровая обработка сигналов : учеб. пособие для вузов / Л.М. Гольденберг, Б.Д. Матюшкин, М.Н. Поляк. – 2-е изд., перераб. и доп. – М. : Радио и связь, 2010. – 256 с.

      Гоноровский, И.С. Радиотехнические цепи и сигналы : учебник для вузов / И.С. Гоноровский. – М. : Радио и связь, 2006. – 512 с.

      Корн, Г. Справочник по математике для научных работников и инженеров ; пер. с англ. / Г. Корн, Т. Корн. – М. : Наука, 200 – 832 с.

      Кремер, Н.Ш. Теория вероятностей и математическая статистика : учебник для вузов / Н.Ш. Кремер. – М. : ЮНИТИ-ДАНА, 2010. – 543 с.

      Марчук, В.И. Итерационный метод выделения функции полезного сигнала в условиях априорной неопределенности / В.И. Марчук // Известия вузов. Северо-Кавказкий регион. Технические науки. – 2007. –№ 9. – С. 25–35.

1