Система фазовой автоподстройки частоты

Введение

Радиопередающие устройства (РПдУ) применяются в сферах телекоммуникации, телевизионного и радиовещания, радиолокации, радионавигации. Стремительное развитие микроэлектроники, аналоговой и цифровой микросхемотехники, микропроцессорной и компьютерной техники оказывает существенное влияние на развитие радиопередающей техники как с точки зрения резкого увеличения функциональных возможностей, так и с точки зрения улучшения ее эксплуатационных показателей. Это достигается за счет использования новых принципов построения структурных схем передатчиков и схемотехнической реализации отдельных их узлов, реализующих цифровые способы формирования, обработки и преобразования колебаний и сигналов, имеющих различные частоты и уровни мощности.

Нелинейная модель системы фазовой автоподстройки частоты

Анализ линейной модели может дать полную информацию о работе САР в режиме малых отклонений от установившегося состояния. Однако для исследования таких явлений, как захват и срыв слежения, линейная модель непригодна. В этом случае необходимо обращаться к нелинейной модели. Так как нелинейная модель описывается нелинейным дифференциальным уравнением, то стараются эту модель не усложнять. Поэтому в модели, как правило, учитываются нелинейные свойства только одного элемента.

ФД ФНЧ УПТ ПГ

Рис. 1

 2  0 U>фд> U>m>>фд> -U>m>>фд>

Рис. 2

Из всех систем радиоавтоматики самой распространенной является система фазовой автоподстройки частоты (ФАПЧ), представленная на рис. 1.Выходное напряжение фазового дискриминатора зависит от раз

ности фаз входных колебаний. Часто используется косинусоидальная дискриминационная характеристика фазового дискриминатора: U_>фд> = = U_>m>_>фд>cos (рис. 2).

1 p сos U>m>>фд> 1+pT>фнч> K>упт>К>пг> 1+pT>пг> >н> >н>  >пг>

Рис. 3

Нелинейная модель системы ФАПЧ изображена на рис. 3. В этой модели фазо-вый дискриминатор отображается последовательным соединением вычитающего устройства, интегратора и нелинейного элемента в соответствии с его математическим описанием

,

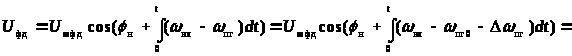
где _>н> – начальная разность фаз,

_>н> = _>вх> - _>пг0> – начальная расстройка,

_>пг0> – частота перестраиваемого генератора при нулевом управляющем напряжении.

Значение начальной разности фаз определяет знак обратной связи. Если 0<_>н><, то, как видно из рис. 2, тангенс угла наклона дискриминационной характеристики отрицательный и, следовательно, обратная связь положительна. При <_>н><2 обратная связь отрицательна. Значит, разность фаз в установившемся режиме _>уст> будет находиться в диапазоне (,2) или отличающемся от него на величину, кратную 2. Начальная расстройка _>н> определяет величину входного процесса интегратора и, следовательно, начальную скорость изменения разности фаз .

Рассмотрим процессы в идеализированной системе ФАПЧ, для которой постоянные времени Т_>фнч> и Т_>пг> равны нулю. Модель идеализированной системы ФАПЧ представлена на рис. 4.

1 p сos >н> >н>  >пг> >у>

Рис. 4

В этой модели произведение U_>m>_>фд>К_>упт>К_>пг>, равное максимальному отклонению частоты перестраиваемого генератора, обозначено через _>у> – полосу удержания. Полоса удержания – это максимальная начальная расстройка, которая компенсируется системой ФАПЧ. По этой модели составляется дифференциальное уравнение в операторной форме:

.

Учитывая, что р – оператор дифференцирования и р_>н> = 0, получаем:

связь фаза автоподстройка

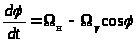. (1)

Система ФАПЧ в установившемся режиме поддерживает разность фаз входных колебаний постоянной. Следовательно, в установившемся режиме d/dt = 0 и, как следует из уравнения (17), _>н> - _>у>cos_>уст> = 0. Отсюда разность фаз в установившемся режиме

_>уст> = arccos(_>н>/_>у>). (2)

Постоянство разности фаз в установившемся режиме означает, что _>пг> = = _>вх>. Режим, при котором расстройка в установившемся состоянии равна нулю, а разность фаз постоянна, называется режимом удержания.

Переходные процессы в системе можно исследовать, пользуясь фазовым портретом системы. Решение дифференциального уравнения (19) изображается на плоскости, декартовыми координатами которой являются искомая функция  и ее производная d/dt. В любой момент времени состояние системы характеризуется определенными значениями разности фаз колебаний  и мгновенной расстройки d/dt и на плоскости отображается точкой, которую называют изображающей. С течением времени  и d/dt изменяются, и изображающая точка перемещается по плоскости. Траектория движения этой точки называется фазовой траекторией. Совокупность фазовых траекторий, построенных для различных начальных условий, образует фазовый портрет системы.

А В С ,рад >уст1> >неуст> >уст2> d/dt,рад/с >у> ->у> >н> 0  2 1 3 2

Рис. 5

Фазовый портрет идеализированной системы ФАПЧ строится по уравнению (19), которое теперь надо понимать как алгебраическое, связывающее независимую переменную  и зависимую переменную d/dt. Линия фазовых траекторий представляет собой, как видно из уравнения (19), перевернутую косинусоиду с амплитудой _>у>, приподнятую на величину начальной расстройки _>н>. На рис.42 изображен фазовый портрет для _>н> = _>у>/2. Стрелками показано направление движения изображающей точки. Это направление определяется по формальному правилу: если производная функции положительна, то функция растет. В верхней полуплоскости d/dt > 0 и изображающая точка движется в сторону возрастания , а в нижней полуплоскости – в сторону уменьшения , так как d/dt < 0.

В фазовом портрете существуют точки, в которые входят и из которых выходят фазовые траектории. Эти точки называются особыми, они соответствуют состояниям равновесия. Особые точки, в которые входят фазовые траектории, называются устойчивыми особыми точками, и они соответствуют устойчивым состояниям равновесия. Заметим, что устойчивые особые точки находятся в том диапазоне разностей фаз, где, как мы отмечали ранее, обратная связь отрицательна.

Прослеживая движение изображающей точки, можно определить, как будут изменяться во времени разность фаз  (горизонтальная координата изображающей точки) и мгновенная расстройка d/dt (вертикальная координата изображающей точки). Начальное состояние системы отображается точкой, находящейся на линии d/dt = _>н>. Так как начальная точка не находится на фазовой траектории (за исключением двух точек в интервале 2), то возникает вопрос, как же точка попадет на фазовую траекторию. Обратимся к процессам, происходящим в идеализированной системе ФАПЧ. В идеализированной системе при ее замыкании мгновенно появляется напряжение на выходе фазового дискриминатора и мгновенно изменяется частота перестраиваемого генератора. Разность фаз при этом не успевает измениться и остается равной _>н>. Следовательно, изображающая точка переместится на фазовую траекторию по вертикальной линии. Например, если _>н> =  (точка 1 на рис. 5), то изображающая точка из своего начального положения 1 переместится по вертикальной линии на фазовую траекторию и далее будет двигаться по фазовой траектории к точке С. В установившемся ре-

t 1 3 2 ,рад  3/2 /2 >уст1> -/2 >уст2> 3 2 t d/dt,рад/с 1 ->у>/2 >у>/2 >у> 3>у>/2

Рис. 6

жиме разность фаз будет равна _>уст2>. Если _>н> = 0, то изображающая точка из своего начального положения 2 вертикально вниз перейдет на фазовую траекторию и будет двигаться по ней к устойчивой особой точке А. Строго говоря, то, что мы называем фазовой траекторией, представляет собой не одну траекторию, а бесконечное множество слившихся фазовых траекторий, соответствующих различным значениям _>н>.

Скорость движения изображающей точки по фазовой траектории непостоянна. Чем больше d/dt, тем быстрее изменяется разность фаз  и быстрее движется изображающая точка. Другими словами, чем дальше от оси  находится изображающая точка, тем быстрее она движется. При приближении к горизонтальной оси скорость ее движения уменьшается до нуля.

Руководствуясь этим правилом, можно приближенно построить переходные процессы в системе (см. рис. 6). Пусть начальная разность фаз _>н> = /2. Изображающая точка из своего начального положения (точка 3 на рис.5) будет двигаться по фазовой траектории вверх. При этом ее вертикальная координата d/dt будет увеличиваться. В переходном процессе d/dt – это тангенс угла наклона зависимости (t). Следовательно, тангенс угла наклона будет расти, и (t) будет изменяться с увеличивающейся крутизной. Крутизна будет расти до тех пор, пока изображающая точка не достигнет вершины фазовой траектории, то есть пока  не станет равным . При дальнейшем движении изображающей точки d/dt уменьшается и разность фаз изменяется с уменьшающейся крутизной. Мгновенная расстройка d/dt сначала увеличивается от _>н> до _>н>+_>у>, принимая максимальное значение при  = , и затем уменьшается до нуля. Переходные процессы зависят от начальной разности фаз. Они показаны на рис.6 для _>н> =  (кривые 1) и для _>н> = 0 (кривые 2). При t = 0 мгновенная расстройка изменяется скачком.

С увеличением начальной расстройки фазовые траектории поднимаются, устойчивая и неустойчивая особые точки сближаются. При _>н>=

,рад  2 3 d/dt,рад/с >у> 2>у> >н> 0

Рис. 7

= _>у> эти особые точки сольются в одну полуустойчивую особую точку. Такой фазовый портрет соответствует режиму захвата. При _>н> > _>у> фазовая траектория проходит над осью , особых точек нет, разность фаз неограниченно возрастает, а мгновенная расстройка изменяется от _>н> - _>у> до _>н> + _>у>. Такой режим называется режимом биений.

На рис. 44 изображен фазовый портрет для _>н> = 1,5_>у>, и на рис. 45 – переходные процессы при _>н> = 0. Максимальная скорость изменения разности фаз будет при  = (2n + 1), а минимальная – при  = 2n.

t ,рад  /2 3/2 2 5/2 3 0 d/dt,рад/с >у> 2>у> 0 t

Рис. 8

Мы рассмотрели процессы в идеализированной системе ФАПЧ. В реальной системе всегда существует фильтр нижних частот. Допустим, в качестве ФНЧ используется интегрирующая цепь с постоянной времени Т. Не вдаваясь в подробности математического описания, отметим только физическую сущность изменений в переходных процессах. Как было сказано, в идеализированной системе изображающая точка, если она вначале не находится на фазовой траектории, переходит на нее по вертикальной линии. Это означает, что изменение мгновенной расстройки происходит настолько быстро, что разность фаз за это время не успевает измениться. С введением ФНЧ управляющее напряжение будет изменяться уже не мгновенно. Также не мгновенно будет изменяться и частота перестраиваемого генератора. Значит, за время изменения частоты изменится и разность фаз. В системе с широкополосным фильтром (_>у>Т<<1) изменение частоты перестраиваемого генератора происходит достаточно быстро и фазовые траектории незначительно отличаются от фазовых траекторий для идеализированной системы. На рис.46 изображены фазовые траектории при _>н> = . Цифрой 1 обозначена фазовая траектория для широкополосной системы. С дальнейшим увеличением постоянной времени Т процессы становятся более медленными, колебательными (фазовая траектория 2). А в узкополосной системе (_>у>Т>>1) изменение напряжения на выходе ФНЧ и, следовательно, изменение частоты перестраиваемого генератора столь незначительны, что не смогут скомпенсиро-

d/dt,рад/с >у> >у>/2 3>у>/2 ,рад  2 0 ->у>/2 1 2 3

Рис. 9

вать начальную расстройку, и система будет находиться в режиме биений (кривая 3).

,рад d/dt,рад/с >у> >н> 

Рис. 10

Характерной фазовой траекторией, позволяющей определить, в каком режиме будет находиться система ФАПЧ, является фазовая траектория, выходящая из полуустойчивой особой точки. Если эта фазовая траектория входит в следующую устойчивую особую точку, то система будет находиться в режиме удержания. Если она входит в следующую полуустойчивую особую точку, то система будет находиться в режиме захвата (рис. 10). Если же фазовая траектория пройдет над следующей полуустойчивой особой точкой,то система будет находиться в режиме биений.

Начальная расстройка, при которой система ФАПЧ переходит из режима биений в режим удержания при уменьшении начальной расстройки, называется полосой

 U U>у макс> >у> >з> >пг>=К>пг>U>у> U>у>() 0 2 1

Рис. 11

захвата. Чем уже полоса пропускания ФНЧ, тем меньше полоса захвата. Качественно это можно пояснить, сравнивая амплитуду напряжения на выходе ФНЧ (линия 2 на рис. 11) с напряжением, требуемым для компенсации начальной расстройки (линия 1 на рис. 11). Если К_>фнч>(_>у>) = 1, то амплитуда напряжения на выходе ФНЧ равна U_>m>_>фд> и этого напряжения достаточно для компенсации начальной расстройки, равной _>у>. Значит, полоса захвата з равна полосе удержания _>у>. Если К_>фнч>(_>у>) < 1, то амплитуда напряжения на выходе ФНЧ меньше напряжения, требуемого для компенсации начальной расстройки, равной _>у>, и в системе сохранится режим биений. При уменьшении начальной расстройки увеличивается амплитуда напряжения на выходе ФНЧ и требуется меньшее напряжение для ее компенсации. Когда амплитуда напряжения на выходе ФНЧ сравняется с требуемым для перестройки значением напряжения, в системе ФАПЧ может произойти захват. Конечно, такая оценка полосы захвата очень грубая, так как не учитывает изменения формы напряжения на выходе ФД при подходе к режиму захвата.

Исследование системы ФАПЧ производится на модели, показанной на рис. 12.

Рис. 12

На вход модели можно подавать постоянную и линейно изменяющуюся

Заключение

Основным направлением развития систем связи является обеспечение множественного доступа, при котором частотный ресурс совместно и одновременно используется несколькими абонентами. К технологиям множественного доступа относятся TDMA, FDMA, CDMA и их комбинации. При этом повышают требования и к качеству связи, т.е. помехоустойчивости, объему передаваемой информации, защищенности информации и идентификации пользователя и пр. Это приводит к необходимости использования сложных видов модуляции, кодирования информации, непрерывной и быстрой перестройки рабочей частоты, синхронизации циклов работы передатчика, приемника и базовой станции, а также обеспечению высокой стабильности частоты и высокой точности амплитудной и фазовой модуляции при рабочих частотах, измеряемых гигагерцами. Что касается систем вещания, здесь основным требованием является повышение качества сигнала на стороне абонента, что опять же приводит к повышению объема передаваемой информации в связи с переходом на цифровые стандарты вещания. Крайне важна также стабильность во времени параметров таких радиопередатчиков - частоты, модуляции. Очевидно, что аналоговая схемотехника с такими задачами справиться не в состоянии, и формирование сигналов передатчиков необходимо осуществлять цифровыми методами.

Список литературы

Коновалов Г.Ф. Радиоавтоматика: Учебник для вузов. – М.: Радиотехника, 2003.

Первачев С.В. Радиоавтоматика: Учебник для вузов. – М.: Радио и связь, 1982.

Радиоавтоматика: Учебное пособие/ Под ред. В.А.Бесекерского. – М.: Высшая школа, 1985

Гришаев Ю.Н. Синтез частотных характеристик линейных систем автоматического регулирования: Метод. указания / РГРТА, 2000

Гришаев Ю.Н. Системы радиоавтоматики и их модели: учебное пособие.: Рязань,1977.

Гришаев Ю.Н. Радиоавтоматика. компьютерный лабораторный практикум/ РГРТА.: Рязань, 2004