Преобразователи напряжение-ток
Содержание
Введение
1. Простейшие преобразователи напряжения в ток
2. ПНТ на основе дифференциальных каскадов
3. Повышение линейности ПНТ
4. Исследование ПНТ
Библиографический список
Введение
Преобразователи напряжение-ток (ПНТ) также являются важным элементом в схемотехнике аналоговых электронных устройств. На их основе могут быть выполнены различные прецизионные операционные усилители, в которых ПНТ используется как входной дифференциальный каскад; ПНТ органично входят в структуры АПН и могут использоваться в различных измерительных схемах.
1. Простейшие преобразователи напряжения в ток
Принцип преобразования напряжения в ток может быть проиллюстрирован с помощью простейшего усилительного каскада на одиночном транзисторе (рис. 1). (Отметим, что резистор R1 выполняет функцию подключения коллектора к шине питания; он достаточно низкоомный и служит как датчик тока при измерении тока коллектора.)

Рис. 1. Простейший преобразователь напряжение-ток на одиночном транзисторе
Предположим, что напряжение смещения UC транзистору обеспечивает источник сигнала UС. Тогда для тока эмиттера IЭ транзистора может быть записано следующее уравнение:
 .
(1)
.
(1)
Оценивать качество преобразования входного напряжения в выходной ток (ток коллектора IK транзистора) наиболее просто, находя крутизну прямого преобразования S:

при условии, что 1.
Находить производную от выражения (1) в явном виде – достаточно громоздкая процедура, поэтому можно найти производную dUC/dIk, а затем взять обратную величину:
 ,
,
то есть
 .
(2)
.
(2)
Выражение (2) показывает, что качество преобразования входного напряжения в выходной ток существенным образом зависит от дифференциального сопротивления эмиттера транзистора, которое, в свою очередь, зависит от тока эмиттера, а следовательно, от входного напряжения. Таким образом, простейший ПНТ обладает двумя существенными недостатками:
нелинейностью крутизны преобразования;
отсутствие возможности осуществлять преобразование двухполярных сигналов.
2. ПНТ на основе дифференциальных каскадов
Обеспечить преобразование двухполярных сигналов можно с помощью ПНТ на основе дифференциального каскада с последовательной отрицательной обратной связью по току в эмиттерной цепи (рис. 2а).


а) б)
Рис. 2. Преобразователь напряжение-ток а) и его проходная характеристика б)
Для схемы ПНТ (рис. 2а), воспользовавшись вторым правилом Кирхгофа, можно записать следующее уравнение для узловых потенциалов:
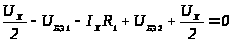 ,
(3)
,
(3)
где T – температурный потенциал;
IХ – приращение тока через резистор R1 при воздействии входного напряжения UX.
С учётом того, что разность напряжений база-эмиттер можно представить как:
 ,
,
проходная характеристика такого звена (рис. 2б) может быть представлена следующим образом:
 .
(4)
.
(4)
Очевидно, что нелинейная составляющая в проходной характеристике определяется первым слагаемым в выражении (4).
Достаточно удобным способом оценки погрешности такого преобразователя, обусловленной нелинейностью, может служить нахождение отклонения реальной функции IХ /I0 (кривая 2 на рис. 2б) от её линейного приближения (кривая 1 на рис. 1б). Отметим, что кривая 2 (рис. 2б) представляет собой разность выходных токов коллекторов транзисторов дифференциальной пары.
Отклонение от линейности можно представить следующим образом:
 ,
(5)
,
(5)
где SX=dIX /dUX – крутизна прямой передачи, определяемая из выражения (4);
IX – абсолютное отклонение тока;
S0 =I0 /U0 – крутизна прямой передачи при линейном приближении;
I0 – максимальный выходной ток преобразователя при подаче на вход максимального напряжения U0.
Отметим, что SX(0) = S0, поэтому:
 ;
(6)
;
(6)
 ,
(7)
,
(7)
где rE = T/I0 – дифференциальное выходное сопротивление транзисторов VT1, VT2 со стороны эмиттера при начальном токе I0; X=IX/I0.
Подставляя (6) и (7) в (8), получаем:
 ,
(8)
,
(8)
поскольку при << 1 можно положить IX/I0 UX/U0.
Формула (5) справедлива при относительно малых погрешностях преобразования – меньше 2-3 %. В этом случае при моделировании относительное отклонение от линейности можно представить как:
преобразователь ток напряжение
 ,
(8а)
,
(8а)
где SМАКС – максимальное значение крутизны на участке U0.
Из (8) следует, что приемлемых уровней погрешности (меньше 0,1 %) можно достичь только при выполнении условий: R1/2rE > 500 и относительном изменении тока X<0,75. Для ПНТ, работающих при питающих напряжениях 15 В, эти условия могут быть легко реализованы. Для низковольтных схем (при их питании от напряжений меньше 5 В) выполнение этих условий приведёт к резкому снижению крутизны преобразования входного напряжения в выходной ток, повышению уровня шумов и т.д.
Основная погрешность линейности преобразования рассмотренного ПНТ обусловлена существенной режимной зависимостью rE от тока эмиттера.
3. Повышение линейности ПНТ
Каким же образом можно уменьшить влияние дифференциального сопротивления эмиттера на работу подобного ПНТ?
Одним из способов снижения влияния дифференциального сопротивления эмиттеров транзисторов служит введение отрицательной обратной связи.
Упрощённая принципиальная схема ПНТ с операционными усилителями в цепи обратной связи приведена на рисунке 3.

Рис. 3. Упрощённая схема ПНТ с операционными усилителями
В этой схемотехнической конфигурации повышение линейности достигается за счёт того, что разность напряжений между входами операционного усилителя имеет достаточно малое значение, которое практически не меняется, значение дифференциального сопротивления эмиттера делится в петлевое усиление раз, что можно описать выражением:
 ,
(9)
,
(9)
где К – коэффициент усиления по напряжению операционного усилителя.
Из (9) можно получить выражение для крутизны преобразования входного напряжения в ток:
 ,
(10)
,
(10)
то есть влияние нелинейной составляющей ослабляется в петлевое усиление раз.
С точки зрения линейности, такая схема обладает наилучшей линейностью преобразования напряжения в ток (при достаточно большом коэффициенте усиления операционного усилителя), практически не требует настройки, однако достаточно сложна и обладает полосой пропускания, определяемой операционным усилителем.
На рисунке 4 приведён достаточно простой вариант реализации такой схемы при интегральном исполнении, однако, как видно из рисунка, он весьма громоздок, причём на рисунке отсутствуют реальные источники тока.

Рис. 4. Схема ПНТ с линеаризацией крутизны преобразования за счёт ООС
В связи с вышеизложенным схему ПНТ (рис. 4) целесообразно использовать только при интегральном исполнении. Кроме того, следует помнить, что частотные свойства такого преобразователя будут не очень хорошими по сравнению с ПНТ на одиночном дифференциальном каскаде.
Другой способ устранения нелинейности преобразования демонстрируется схемой ПНТ, представленной на рисунке 5. Этот способ компенсации нелинейности получил достаточно широкое распространение [19, 20]. Суть его заключается в следующем: тем или иным способом формируется компенсирующий ток, ослабляющий влияние изменения rE дифференциального каскада при изменении тока эмиттера.
Работает схема ПНИ (рис. 5) следующим образом. Транзисторы VT1 и VT6, образующие дифференциальный каскад, с помощью резистора R1 осуществляют преобразование входного напряжения в выходной ток. Транзисторы VT2 и VT5 включены по схеме с общей базой и передают токи коллекторов транзисторов VT1 и VT6 на выход с коэффициентом передачи α 1. Одновременно с этим при изменении токов эмиттеров транзисторов VT2 и VT5 меняются и их напряжения база-эмиттер. В этом случае меняется и разность напряжений база-эмиттер транзисторов VT2 и VT5, причём в зависимости от знака приращения входного напряжения UX разность напряжений база-эмиттер транзисторов VT2 и VT5 также меняет знак. Вспомогательный дифференциальный каскад на транзисторах VT3 и VT4 с помощью резистора RK преобразует напряжение, пропорциональное разности баз-эмиттер транзисторов VT2 и VT5, в ток, который перекрёстным образом отправляется на токовые выходы ПНТ. Поскольку в базовой схеме ПНТ на транзисторах VT1 и VT6 присутствует составляющая, обусловленная UБЭ1,6 этих транзисторов, то при условии, что транзисторы VT2 и VT5 в точности идентичны транзисторам VT1 и VT6, а токи источников опорного тока одинаковы, выбором сопротивления резистора RK можно скомпенсировать влияние UБЭ1,6.

Рис. 5. ПНТ с линеаризацией влияния дифференциального сопротивления эмиттеров транзисторов дифференциального каскада
Оценку нелинейности преобразования напряжения в ток для схемы рисунка 5 можно произвести следующим образом. Рассмотрим следующие уравнения:
 ;
(11)
;
(11)
 ,
(12)
,
(12)
где
 – разность напряжений база-эмиттер
транзисторов VT2
и VT5;
– разность напряжений база-эмиттер
транзисторов VT2
и VT5;
IK – компенсирующий ток вспомогательного дифференциального каскада на транзисторах VT3 и VT4; К = IK/I0, Х = IX/I0.
Суммарный выходной ток ПНТ c учётом знаков приращений можно представить как I = IX - IK, откуда из (11) и (12) следует:
 .
(13)
.
(13)
Поскольку (1+К) 1, последнее слагаемое в выражении (13) можно разложить в ряд. Тогда выражение (13) представить как:
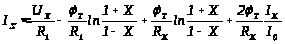 .
(14)
.
(14)
Так как IK =IX - I, а Т/I0=rE, выражение (14) может быть преобразовано к виду:
 .
(15)
.
(15)
При выполнении условия:
 (16)
(16)
второе слагаемое в выражении (15) обращается в нуль, поэтому результирующая крутизна преобразования напряжения в ток не будет зависеть от уровня входного сигнала.
Так как выражение (15) было получено при определённых допущениях (например, всех транзисторов не зависят от тока и равны единице), выполнение условия (14) не исключает полную независимость крутизны от уровня входного напряжения. Однако погрешность преобразования можно сделать достаточно малой, что подтверждается результатами моделирования рассмотренных схем (рис. 6).
Графики, приведённые на рисунке 6, по сути, представляют собой отклонение в процентах нормированной крутизны прямой передачи от единицы, что при U0 = 1 совпадает с выражением (8). Для схемы рисунка 2а максимальное отклонение составляет 0,75 %, а для схемы ПНТ рисунка 5 – не превышает 0,015 %.

Рис. 6. Графики, иллюстрирующие отклонение от линейности схем ПНТ рисунка 2а () и ПНТ рисунка 5 (□)
Следует также отметить, что для схемы ПНТ, приведённой на рисунке 5, достаточно точное выражение для отклонения от линейности может быть получено из выражений (13) и (14) после аппроксимации их полиномами четвёртой степени. В этом случае можно дать следующие рекомендации. Условие (16) даёт приближённое значение сопротивлений резисторов R1 и RK, а дальнейшую параметрическую оптимизацию можно осуществить, добиваясь, чтобы значения отклонения на краях диапазона совпадали со значение отклонения в точке UX = 0. Это будет наилучшее приближение к линейной функции [21].
Некоторый недостаток схемы ПНТ (рис. 5) – наличие четырёх идентичных источников тока, которые, с одной стороны, повышают энергопотребление схемы, с другой – их неидентичность нарушит выполнение условий компенсации нелинейности во всём диапазоне входных напряжений.
Отметим, что для качественной работы подобных схем ПНТ важна абсолютная идентичность (симметричность) каналов усиления для положительных и отрицательных приращений входного сигнала.
Дабы уйти от необходимости использовать четыре согласованных источника тока, можно воспользоваться способом, реализованным в схемах ПНТ, приведённых на рисунках 7 и 8 [22, 23].

Рис. 7. Схема высоколинейного ПНТ с делителями тока в коллекторной цепи для компенсации нелинейной составляющей крутизны преобразования
Работу схемы рисунка 7 можно пояснить следующим образом. Транзисторы VT1 и VT2 образуют дифференциальный каскад, который с помощью резистора R0 осуществляет преобразование входного напряжения в ток коллекторов названных транзисторов. В коллекторные цепи транзисторов VT1 и VT2 включены делители тока на транзисторах VT3, VT4, VT5 и VT6, VT7, VT8 (обведены пунктиром на рисунке 7).
Делители тока представляют собой токовое зеркало Вильсона, которое питается «снизу» от источника тока, поэтому ток коллектора транзистора VT1 (VT2) перераспределяется между транзисторами VT4 и VT5 (VT8 и VT6) в зависимости от отношения площадей эмиттеров транзисторов VT3 и VT5 (VT7 и VT6).
Таким образом, часть тока, пропорциональная входному напряжению UX, ответвляется с помощью делителей тока, и на транзисторах VT9 и VT10 выделяется разность напряжений база-эмиттер, являющаяся функцией приращения выходного тока IX. С помощью резистора RК формируется компенсирующий ток, так что разносное приращение токов на выходе можно представить выражением:
 ,
(17)
,
(17)
где К < 1 – коэффициент деления в делителях тока.
Третье слагаемое в правой части выражения (17) и есть компенсирующий ток. Очевидно, что, если выполнить условие:
 ,
,
слагаемые, содержащие логарифм, обращаются в нуль, в результате крутизна прямого преобразования:
 ,
(18)
,
(18)
что несколько меньше, чем в базовой схеме ПНТ (рис. 2а), в связи с чем К рекомендуется выбирать меньше 0,5 (например 0,1…0,2).
Схожей по принципу действия оказывается схема ПНТ (рис. 8). Здесь делитель тока выполнен непосредственно в дифференциальном каскаде, а принцип формирования компенсирующего тока аналогичен предыдущему случаю.

Рис. 8. Схема высоколинейного ПНТ с делителями тока в дифференциальном каскаде для компенсации нелинейной составляющей крутизны преобразования
Отметим, что в этом случае выбором площадей эмиттеров пар транзисторов VT1 и VT2 (VT3 и VT4) коэффициент деления Кi опорного тока I0 для соответствующего плеча дифференциального каскада выбирается из условий:
 ,
,
где Si – площадь эмиттера соответствующего транзистора.
Очевидна необходимость в том, чтобы S1 > S2 (S4 > S3), так как и в этом случае из-за деления выходных токов дифференциального каскада результирующая крутизна несколько снижается и определяется выражением (15), причём К=S2/S1 = S3/S4.
Формировать компенсирующий ток можно и в эмиттерных цепях базового дифференциального каскада, как это показано на рисунке В этом случае часть компенсирующего тока попадает в эмиттер дифференциального каскада, а часть тока, обусловленная коэффициентом передачи делителя тока на транзисторах VT7, VT8 (VT9, VT10), перекрёстно отправляется в коллекторы транзисторов дифференциальной пары. За счёт этого удаётся незначительно снизить крутизну преобразования при достаточно высокой линейности. Отметим, что последняя схема ПНТ обладает наибольшим динамическим диапазоном входного сигнала из ранее рассмотренных при одинаковом отклонении от линейности.

Рис. 9. Схема ПНТ, формирующая компенсирующие токи в эмиттерных цепях дифференциального каскада
Фактически вся компенсирующая цепь обеспечивает неизменность тока эмиттера транзисторов дифференциальной пары при изменении входного напряжения. Действительно, если входное напряжение UX растёт, растёт и эмиттерный ток транзистора VT1 за счёт приращения тока через резистор R0. Одновременно с этим растёт напряжение и на базе транзистора VT10 (на базе транзистора VT7 напряжение соответственно уменьшается), что приводит к уменьшению тока эмиттера транзистора VT7 за счёт появления приращения тока через резистор RK и к снижению тока эмиттера транзистора VT1. Таким образом, ток эмиттера транзистора VT1, наряду с положительным приращением тока через резистор R0, получает отрицательное приращение тока через коллектор транзистора VT7, и при правильном выборе резистора RK ток эмиттера транзистора VT1 перестаёт зависеть от входного напряжения. Естественно, ток эмиттера транзистора VT2 зависит от входного сигнала «с точностью до наоборот», в результате чего влияние режимно зависимых дифференциальных сопротивлений эмиттеров транзисторов VT1 и VT2 исключается.
Условие максимальной линейности можно получить из выражения для разности выходных токов ПНТ:
 ,
(19)
,
(19)
где К<1 – коэффициент передачи повторителей тока на транзисторах VT7, VT8 и VT9, VT10.
Собственно условие компенсации определяется выражением:
 .
(20)
.
(20)
С учётом (17) линейная составляющая крутизны прямой передачи ПНТ определится как:
 .
.
К сожалению, предложенные схемы не лишены недостатка: за высокую линейность и малое токопотребление приходится «платить» снижением крутизны преобразования на 30–40 %. Если вместо делителя тока в схеме ПНТ использовать ответвитель тока (рис. 10), то наряду с повышением линейности крутизну преобразования можно повысить в два-три раза. Эта схема носит чисто иллюстративный характер, чтобы показать широкие возможности методов компенсации нелинейных составляющих схемной функции крутизны преобразования входного напряжения в выходной ток.

Рис. 10. Схема ПНТ с ответвителями тока
Для определения условий компенсации нелинейности в этой схеме необходимо решить систему трансцендентных уравнений, что можно сделать только численно. Однако принцип функционирования также похож на предыдущие. Ответвители тока на транзисторах VT3, VT4, резисторе R3 и VT5, VT6, резисторе R4 имеют нелинейную характеристику, причём такую, что дифференциальный коэффициент передачи тока транзистора VT1 (VT2) имеет отрицательный знак, поэтому приращения токов транзистора VT1 и VT4 с помощью транзисторов VT7, VT8 складываются (а не вычитаются, как в предыдущих случаях). За счёт этого крутизна прямой передачи ПНТ возрастает. С помощью транзисторов VT8, VT9 и резистора RК формируется компенсирующий ток, пропорциональный Т, так что выполняется условие частичной нейтрализации влияния режимно зависимых сопротивлений эмиттеров транзисторов дифференциального каскада. Ещё одним недостатком подобных схем ПНТ является необходимость использовать транзисторы p-n-p типа, что в большинстве случаев ограничивает частотный диапазон схемы.
Ещё одним перспективным направлением построения высоколинейных ПНТ являются мостовые преобразователи (рис. 11).

Рис. 11. Схема мостового ПНТ
Схема мостового преобразователя напряжение-ток изначально имеет меньшую погрешность преобразования в сравнении с базовой схемой на основе дифференциального каскада, так как в мостовой схеме осуществляется взаимная компенсация выходного сопротивления транзисторов, являющегося основным источником погрешности. Отметим, что резисторы R4 и R5 включены в схему только как датчики тока.
Можно показать, что ток, протекающий через резистор R2, определяется как:
 ,
(21)
,
(21)
где
 – соответственно объёмные сопротивления
баз транзисторов n-p-n
и p-n-p
типов.
– соответственно объёмные сопротивления
баз транзисторов n-p-n
и p-n-p
типов.
Если в первом приближении пренебречь объёмным сопротивлением баз транзисторов, то в выражении (21) исчезает квадратичная (нелинейная) составляющая тока через резистор R2. То есть выходное сопротивление со стороны эмиттеров транзисторов VT1 и VT8 (VT4 и VT6) в первом приближении постоянно и не зависит от уровня входного сигнала.
Существенным недостатком мостового преобразователя является то, что его крутизна в два раза ниже в сравнении с дифференциальным каскадом. В самом деле, приращение тока IX через резистор R2 возникает за счёт того, что ток эмиттера транзистора VT1 получает приращение +IX/2, а ток эмиттера транзистора VT8 получает приращение -IX/2. По аналогии: только с противоположными знаками происходят приращения токов в транзисторах VT4 и VT6 соответственно.
Устранить этот недостаток можно за счёт введения повторителей тока на транзисторах VT13, VT12 и VT14, VT11, выходы которых включены перекрёстно к выходам ПНТ и добавляют в выходной ток составляющую, пропорциональную IX.
Использование резистора R16 придаёт нелинейные свойства повторителю тока, что позволяет дополнительно компенсировать нелинейность преобразователя при одновременном повышении крутизны преобразования в заданное число раз.
Кроме того, динамический диапазон мостовых ПНТ по входному сигналу теоретически может достигать диапазона ЕП, что принципиально недостижимо в преобразователях напряжение-ток на основе дифференциального каскада. Это особенно важно при проектировании низковольтных прецизионных схем.
На рисунке 12 представлены результаты моделирования схемы мостового ПНТ.

Рис. 12. Графики, иллюстрирующие отклонение от линейности мостового и базового ПНТ на основе дифференциального каскада
Моделирование проведено в сравнении с базовой схемой на основе дифференциального каскада при одинаковой крутизне преобразования и близких статических токах выходных транзисторов той и другой схемы. Погрешность крутизны преобразования для базовой схемы достигает 20 %, а для схемы мостового преобразователя – менее 0,01 % (нижний график рис. 12).
4. Исследование ПНТ
«Соберите» упрощённую схему ПНТ, приведённую на рисунке 2а. Упрощение этой схемы обусловлено применением идеальных источников тока, что существенно не повлияет на изучение принципа её работы. Обратите внимание: в схему ПНТ в коллекторные цепи необходимо включить одинаковые резисторы сопротивлением 1…10 Ом. Вторые выводы этих резисторов подключаются к положительной шине питания. Резисторы будут выполнять роль датчиков тока и на работу схемы, с точки зрения оценки её линейности, не повлияют.
Параметрический синтез схемы можно провести, воспользовавшись следующими соображениями. Выбрав напряжение питания ±5 В, для удобства оценки крутизны преобразования резистор R1 можно выбрать 1 кОм. Тогда при условии, что изменение входного напряжения будет составлять ±1 В, ток источников опорного тока целесообразно выбрать 2 мА. В этом случае коэффициент использования тока Х 0,5.
В качестве моделей компонентов можно выбрать модели любых интегральных транзисторов, имеющихся в библиотеке моделирующей программы и способных работать при напряжении коллектор-база более 10 В.
Можно рекомендовать следующий порядок изучения и моделирования схемы.
1. Подключите вспомогательные резисторы сопротивлением в несколько килоом между входами ПНТ и общей шиной. Эти резисторы необходимы для создания пути протекания базовых токов транзисторов дифференциальной пары. Функциональный элемент Е1 представляет собой источник напряжения, управляемый напряжением (ИНУН). (Его параметр GANE оставьте по умолчанию равным единице.) Он необходим для того, чтобы создать дифференциальное напряжение между входами ПНТ. В результате у Вас должна получиться схема, представленная на рисунке 13.

Рис. 13. Схема ПНТ, предназначенная для моделирования
В режиме .DC задайте вариацию источника V1 в пределах ±1 В. После выполнения моделирования через меню Trace\Add Trace наберите в командной строке
(1-d(I(R23)- I(R22))/ MAX(d(I(R23)- I(R22))))*100.
Смысл этого выражения в следующем: находятся разность выходных токов, протекающих через резисторы R22 и R23; производная от этой разности, которая нормируется по отношению к максимальному значению производной; отклонение нормированной производной от максимального значения (1) и умножается на 100 %. Такой способ оценки линейности полностью соответствует выражению (5а), полученному аналитическим путём.
Должен получиться график, подобный тому, что представлен на рисунке 14. Отметим, что максимальное отклонение от линейности у вас может получиться иным (несколько больше или меньше) в зависимости от используемых моделей транзисторов, но характер графика будет подобен приведённому на рисунке 14.

Рис. 14. График, иллюстрирующий отклонение от линейности ПНТ рисунка 2а
2. «Соберите» схему ПНТ на основе операционных усилителей (рис. 4). Для сопоставительного моделирования с базовой схемой ПНТ на основе дифференциального каскада в этом же файле представьте схему ПНТ рисунка 2а. У вас должна получиться схема, приведённая на рисунке 15. Поскольку операционные усилители допускают питание от ±15 В, входное напряжение для такой схемы может достигать и ±10 В, если сопротивление резистора R1 и токи источников токов выбраны соответственно. Естественно, если сопротивление резистора R1 выбрать 10 кОм, линейность ПНТ с ОУ будет ещё выше.

а) б)
Рис. 15. Схема для сопоставительного моделирования ПНТ с операционными усилителями в цепи обратной связи а) и базового ПНТ б)
Но для объективного сравнения выберем токи источников токов и преобразующие сопротивления, как и в предыдущем случае, 2 мА и 1 кОм. Результаты сравнительного моделирования схем ПНТ рисунка 15 приведены на рисунке 16.

Рис. 16. Зависимость нормированной крутизны схемы ПНТ рисунка 15а (кривая □) и базовой схемы (б) (кривая ◊)
На рисунке 16 результаты моделирования представлены в иной форме, потому что отклонение от линейности в схеме ПНТ рисунка 15а) будут столь малы (примерно 9,5·10-4 %), что даже в достаточно мощных современных компьютерах возникает проблема вычисления производных. Это приводит к появлению так называемого «цифрового шума», что делает график малоинформативным. В то же время применение курсора на графике показывает, что отклонение нормированного значения крутизны от максимального в схеме ПНТ с ОУ составляет 9,5·10-6, что в процентном отношении соответствует 9,5·10-4 %. При этом в базовой схеме ПНТ отклонение от линейности равно 0,76 %. То есть схема ПНТ с ОУ даёт выигрыш перед базовой схемой примерно в 800 раз.
3. По аналогии с предыдущими случаями проведите сопоставительное моделирование схем ПНТ рисунков 7 и 8, задавая токи и выбирая сопротивления резисторов из тех же соображений, что и ранее.
4. Проведите сопоставительное моделирование мостовой схемы ПНТ (рис. 11), установив значения опорных токов в мостовой схеме 1…2 мА, в базовой схеме – 2 мА.
4.1. Вначале постройте графики крутизны преобразования при закороченных на шину отрицательного напряжения питания баз транзисторов VT13 и VT11. В этом случае повторители тока на транзисторах VT13, VT122 и VT11, VT14 исключаются из схемы.
Постройте графики при изменении входного сигнала в диапазоне ±1 В, затем в диапазоне ±2 В.
Сравните численное значение крутизны преобразования мостовой и базовой схем.
4.2. Сравните отклонение крутизны преобразования от линейного для мостовой и базовой схем при изменении входного сигнала в диапазоне ±1 В, затем в диапазоне ±2 В. Объясните получившиеся результаты.
4.3. Включите в действие повторители тока на транзисторах VT13, VT12 и VT11, VT14, убрав цепи, соединяющие выводы баз транзисторов VT13 и VT11 с шиной отрицательного источника питания. При этом резистор R16 (рис. 11) из схемы удалите.
Оцените изменение численного значения крутизны преобразования мостовой схемы ПНТ при наличии повторителей тока.
Измените отношение площадей эмиттеров транзисторов VT13, VT12 и VT11, VT14 так, чтобы коэффициент передачи повторителей тока стал больше единицы (например, установив в атрибутах модели транзисторов VT11 и VT12 коэффициент AREA =2). Определите, как изменится численное значение крутизны преобразования мостовой схемы ПНТ в этом случае, и объясните почему.
4.4. Установите резистор R16 ориентировочно с номиналом, указанным на схеме рисунка 11. Проведите моделирование и оцените отклонение от линейности мостовой схемы ПНТ. Изменяя сопротивление R16 в пределах 0,1…0,5 %, установите такой вид кривой отклонения от линейности, чтобы значение погрешности на краях диапазона соответствовало значению погрешности в нуле. Этот случай будет соответствовать максимальному линейному приближению.
Библиографический список
Активные RC-фильтры на операционных усилителях / пер. с англ. ; под ред. Г.Н. Алексакова. – М. : Энергия, 2010. – 64 с. : ил.
Алексенко, А.Г. Применение прецизионных аналоговых микросхем / А.Г. Алексенко, Е.А. Коломбет, Г.И. Стародуб. – М. : Радио и связь, 2009. – 256 c.
Аналоговые и цифровые интегральные микросхемы : справ. пособие / Н.А. Барканов [и др.] ; под ред С.В. Якубовского. – 2-е изд., перераб. и доп. – М. : Радио и связь, 2008. – 432 с. : ил. – (Проектирование РЭА на интегральных микросхемах).
Анисимов, В.И. Операционные усилители с непосредственной связью каскадов / В.И. Анисимов, М.В. Капитонов, Ю.М. Соколов, Н.Н. Прокопенко. – Л. : Энергия, 2009. – 168 с. : ил.
Источники вторичного электропитания / под ред. Ю.И. Конева. – М. : Радио и связь, 2010. – 280 с., ил. (Проектирование РЭА на интегральных микросхемах).
Model of BD329. Philips Semiconductor. Product specification (электронный ресурс). – URL : http://www.philips.com/_Models.
Ногин, В.Н. Аналоговые электронные устройства : учеб. пособие для вузов / В.Н. Ногин. – М. : Радио и связь, 2010. – 304 с. : ил.
Полупрововодниковые приборы : диоды, тиристоры, оптоэлектронные приборы : cправочник / под общ. ред. Н.Н. Горюнова. – 2-е изд., перераб. – М. : Энергоатомиздат, 2009. – 744 с. : ил.
Разевиг, В.Д. Применение программ P-CAD и Pspise для схемотехнического моделирования на ПЭВМ. В 4 вып. Вып. 2. Модели компонентов аналоговых устройств / В.Д. Разевиг. – М. : Радио и связь, 2008. – 70 с. : ил.
Разевиг, В.Д. Система сквозного проектирования электронных устройств DesingLab 8.0 / В.Д. Разевиг. – М. : СОЛОН-Р, 2009. – 704 с. : ил. (Серия «Системы проектирования»).
Синтез активных RC-цепей. Современное состояние и проблемы / под ред. А.А. Ланнэ. – М. : Связь, 2010. – 296 с. : ил.
Соклофф, С. Аналоговые интегральные схемы : пер. с англ. / С. Соклофф. – М. : Мир, 2008. – 583 с. : ил.
Старченко, Е.И. PSpice пользователю : пособие / Е.И. Старченко. – Шахты : Изд-во ЮРГУЭС, 2009. – 37 с. : ил.
Старченко, Е.И. Базовые матричные кристаллы. Схемотехника типовых аналоговых микроэлектронных устройств : пособие по изучению теоретической части дисциплины «Аналоговые электронные устройства» / Е.И. Старченко, В.Г. Манжула. – Шахты : ШТИБО, 2010. – 61 с. : ил.
Степаненко, И.П. Основы теории транзисторов и транзисторных схем / И.П. Степаненко. – М. : Энергия, 2010. – 615 с. : ил.
Титце, У. Полупроводниковая схемотехника : пер. с нем. / У. Титце, К. Шенк. – М. : Мир, 2008. – 586 с. : ил.
Шило, В.Л. Линейные интегральные схемы в радиоэлектронной аппаратуре / В.Л. Шило. – 2-е изд., перераб. и доп. – М. : Советское радио, 2009. – 386 с. : ил.
Шкритек, П. Справочное руководство по звуковой схемотехнике : пер. с нем. / П. Шкритек. – М. : Мир, 2010. – 446 с. : ил.
Старченко, Е.И. Принципы проектирования низковольтных прецизионных аналоговых перемножителей напряжения / Е.И. Старченко // Альтернативные естественно возобновляющиеся источники энергии и энергосберегающие технологии, экологическая безопасность регионов : Выездная сессия Секции энергетики Отделения энергетики, машиностроения и процессов управления РАН : материалы сессии, Ессентуки, 12–15 апреля 2008. В 2 ч. Ч. 2 / под ред. Я.Б. Данилевича. – Шахты : Изд-во ЮРГУЭС, 2008. – С. 155–163.
Pat. 4,322,688 US. Cascode Fid-Forward amplifier / G. Kennet Schltzhauer, 2010.