Качество линейных непрерывных САУ и методы их оценки
Качество линейных непрерывных САУ и методы ее оценки
ОЦЕНКА КАЧЕСТВА ЛИНЕЙНЫХ САУ
310181 замкнутый линейный квадратичная интегральная ошибка
Устойчивость является необходимым, но недостаточным условием работоспособности САУ. К ним предъявляют определенные требования качества.
Наиболее полной характеристикой качества системы является текущая ошибка

 (1)
(1)
 - фактическое возмущающее движение
- фактическое возмущающее движение
 - заданное невозмущающее движение
- заданное невозмущающее движение
Если
 ,
где
,
где
 - заданное воздействие, то ошибка
совпадает с величиной на выходе
сравнивающего устройства.
- заданное воздействие, то ошибка
совпадает с величиной на выходе
сравнивающего устройства.
Если на систему действуют два внешних
воздействия - задающее
 и возмущение
и возмущение
 ,
причем
,
причем



 (2)
(2)




 - ошибка от задающего воздействия
- ошибка от задающего воздействия
 -
ошибка от возмущения
-
ошибка от возмущения

Из (2) видно, что ошибка
 зависит как от свойств системы, так и
от видов входных воздействий
зависит как от свойств системы, так и
от видов входных воздействий
 .
Для одной и той же системы она различна
в зависимости от входных воздействий.
Поэтому при определении качества системы
используют так называемые типовые
воздействия:
.
Для одной и той же системы она различна
в зависимости от входных воздействий.
Поэтому при определении качества системы
используют так называемые типовые
воздействия:
-
 - ступенчатое;
- ступенчатое;
-
 - линейное;
- линейное;
-
 - гармоническое.
- гармоническое.
Различают качество системы в переходном и установившемся режимах.
Качество в переходном режиме - свойство
системы на начальном отрезке времени
 ,
где
,
где
 - момент приложения на систему воздействия.
- момент приложения на систему воздействия.
Качество в установившемся режиме - свойство системы в асимптотике при
 .
.
Для оценки качества в переходном режиме
используют ступенчатое воз-действие
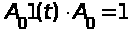 ,
т.к. вид кривой переходного процесса не
зависит от
,
т.к. вид кривой переходного процесса не
зависит от
 .
.
 где
где
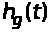 и
и
 - переходные функции.
- переходные функции.


Оценивать качество систем и сравнивать их между собой по текущим ошибкам и переходным функциям неудобно. Поэтому для оценки качества систем используют числовые показатели, которые, так или иначе, определяют характерные свойства ошибок и переходных характеристик.
Прямые показатели качества определяются непосредственно по переходной характеристике.
2. Алгебраические критерии устойчивости
Алгебраическими критериями называются критерии, которые основаны на проверке определенных соотношений, составленных из коэффициентов характеристического уравнения.
Поэтому при использовании алгебраических
критериев нужно иметь только
характеристическое уравнение вида:

Если исследование устойчивости проводится с помощью алгебраических критериев, нужно, прежде всего, проверить выполнение необходимого условия устойчивости, так как его проверка не требует никаких вычислений и при невыполнении этого условия дальнейших исследований проводить не нужно.
Необходимое условие устойчивости. Для того чтобы система была устойчива, необходимо, чтобы коэффициенты ее характеристического уравнения были одного знака:
 или
или
 (3)
(3)
Если необходимое условие не выполняется, то система неустойчива.
Если же необходимое условие выполняется, то система при n 3 (n - порядок системы) может быть устойчивой и неустойчивой и для установления устойчивости нужно воспользоваться каким-либо критерием устойчивости. Как уже установлено, в случае систем первого и второго порядков необходимое условие (3) является и достаточным.
Перейдем к формулировке критерия Гурвица. Составим из коэффициентов характеристического уравнения определитель Гурвица п-го порядка

На главной диагонали к располагаются
коэффициенты в порядке возрастания их
индексов, начиная с
 и кончая
и кончая
 .
В каждом столбце при движении от элемента,
находящегося на главной диагонали,
вверх индексы коэффициентов возрастают,
вниз – убывают. При этом на место
элементов с индексами, превышающими п
(при движении вверх), и отрицательными
индексами (при движении вниз) проставляются
нули.
.
В каждом столбце при движении от элемента,
находящегося на главной диагонали,
вверх индексы коэффициентов возрастают,
вниз – убывают. При этом на место
элементов с индексами, превышающими п
(при движении вверх), и отрицательными
индексами (при движении вниз) проставляются
нули.
Определители Гурвица – это миноры, входящие в главный определитель Гурвица
Запишем главные миноры определителя :
:
 ,
,  ,
,  ,
…
,
…
Эти миноры, включая определитель называются определителями Гурвица.
Примем для определенности
называются определителями Гурвица.
Примем для определенности
 .
Это допущение не нарушает общности, так
как если
.
Это допущение не нарушает общности, так
как если
 ,
то обе части характеристического
уравнения можно умножить на —1.
,
то обе части характеристического
уравнения можно умножить на —1.
Критерий Гурвица. Для того чтобы система была устойчива, необходимо и достаточно, чтобы все определители Гурвица, составленные из коэффициентов ее характеристического уравнения, были больше нуля при
 ):
):
 ,
,
 (2)
(2)
Из этого критерия следует, что при n =3 необходимое и достаточное условие устойчивости имеет вид:
 ,
,
 ,
,
 ,
, 
Следовательно, уже при п = 3 необходимое
условие устойчивости (1) не является и
достаточным. Для устойчивости систем
третьего порядка кроме необходимого
условия (3) должно выполняться неравенство
 ,
(т.е. разность между произведением
средних коэффициентов и произведением
крайних коэффициентов должна быть
положительной).
,
(т.е. разность между произведением
средних коэффициентов и произведением
крайних коэффициентов должна быть
положительной).
Пример: Исследуем устойчивость системы
с единичной отрицательной обратной
связью, в разомкнутом и замкнутом
состояниях, если задана передаточная
функция разомкнутой системы
 .
Характеристическое уравнение разомкнутой
системы:
.
Характеристическое уравнение разомкнутой
системы:
 .
.
Необходимое условие не выполняется:
при
 коэффициент
коэффициент
 .
Поэтому разомкнутая система неустойчива.
.
Поэтому разомкнутая система неустойчива.
Характеристическое уравнение замкнутой
системы
 .
Необходимое условие устойчивости
выполняется. Поэтому достаточно проверить
условие (4):
.
Необходимое условие устойчивости
выполняется. Поэтому достаточно проверить
условие (4):
 ,
,
 ,
,
 ,
,
 .
.
Замкнутая система устойчива.
Критерий Льенара—Шипара. При выполнении необходимого условия (1) для устойчивости системы необходимо и достаточно, чтобы были положительны или все определители Гурвица с четными индексами, или все определители Гурвица с нечетными индексами.
Следовательно, для того чтобы система была устойчива, необходимо и достаточно, чтобы
 ,
,  ,…,
,…,  ;
;  ,
,  ,
,  …
…
Или
 ,
,  ,…,
,…,  ;
;  ,
,  ,
,  …
…
Таким образом, для исследования устойчивости нет необходимости вычислять все определители Гурвица.
3. Оценка качества САУ в переходном режиме. Показатели качества.
Показатели качества в переходном режиме:
1 Прямые показатели качества:
1.1Время регулирования
1.2Перерегулирование
Время регулирования
 - минимальное время, по истечение которого
(с момента подачи ступенчатого воздействия)
отклонение выходной величины от
установившегося значения не превышает
некоторой заданной величины
- минимальное время, по истечение которого
(с момента подачи ступенчатого воздействия)
отклонение выходной величины от
установившегося значения не превышает
некоторой заданной величины
 ,
где
,
где
 - установившееся значение переходной
ха-рактеристики.
- установившееся значение переходной
ха-рактеристики.
Перерегулирование –максимальное отклонение переходной характеристики от установившегося значения
 .
.
Если
 (при
(при
 )
)


Порядок построения переходной характеристики не зависит от места приложения входного воздействия. Поэтому достаточно рассматривать, как строится переходная характеристика при действии какого-либо одного воздействия, например задающего.


Пусть
 - дробно - рациональная функция. Если
полюсы
- дробно - рациональная функция. Если
полюсы

 этой функции простые, то
этой функции простые, то

Если полюсы
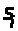 кратные, то формула усложняется (через
предел).
кратные, то формула усложняется (через
предел).
Пример.
Пусть
 - п.ф. разомкнутой системы, тогда п.ф.
замкнутой системы
- п.ф. разомкнутой системы, тогда п.ф.
замкнутой системы



 .
.
2 Косвенные показатели качества:
2.1 Корневые
2.2 Частотные
2.3 Интегральные.
2.1.1 степень устойчивости
Корневые
2.1.2 колебательность
Качество системы можно рассматривать, когда все корни характеристического уравнения левые, т.е. система устойчива.
Степень устойчивости - расстояние от мнимой оси до ближайшего корня
 ,
где
,
где
 - корни характеристического уравнения
- корни характеристического уравнения
характеризует быстродействие системы.
При прочих равных условиях чем больше
 ,
тем быстрее затухает переходной процесс.
,
тем быстрее затухает переходной процесс.
Колебательность - мера склонности системы к колебаниям

2.2 Частотные показатели качества:
2.2.1 Запас устойчивости по амплитуде
2.2.2 Запас устойчивости по фазе.
По ЛАЧХ и ФЛЧХ По АФЧХ

 - частота, при которой сдвиг фазы
- частота, при которой сдвиг фазы

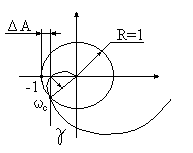
 - частота среза
- частота среза
Чем меньше запасы по амплитуде
и фазе, тем медленнее затухает процесс.

2.3 Интегральные показатели качества.
2.3.1 Интегральная ошибка – определяется
при апериодическом и монотонном
переходном процессе –

2.3.2 Квадратичная интегральная ошибка
– определяется при колебательном
переходном процессе–

Ошибку системы можно представить в виде
суммы
 ,
где
,
где
 - переходная составляющая ошибки;
- переходная составляющая ошибки;
 - установившаяся ошибка.
- установившаяся ошибка.

 - квадратичная интегральная ошибка
- квадратичная интегральная ошибка
