Расчет количественных характеристик надежности

Волжский университет им. В.Н. Татищева

Факультет информатики и телекоммуникации

Кафедра промышленной информатики

Контрольная работа

по дисциплине: Надежность систем

тема: Расчет количественных характеристик надежности

Тольятти

2009

Задание №1

На испытание поставлено изделий. За время t час вышло из строя n(t) штук изделий. За последующий интервал времени вышло из строя изделий. Необходимо вычислить вероятность безотказной работы за время t, частоту отказов и интенсивность отказов на интервале . Исходные данные для решения задачи приведены в таблице 1.

Таблица 1. Исходные данные для задачи 1

№ вар	N>0>	t, час	,час	n()
18	45	5	5	5

Решение

Вероятность безотказной работы :

=(45-5)/45=0,888888889

Частота отказов на интервале :

=5/(45*5)= 0,022222222

Интенсивность отказов на интервале :

=0,022222222/0,888888889=0,0250000

Задание №2

Изделие состоит из N элементов, средняя интенсивность отказов которых . Требуется вычислить вероятность безотказной работы в течение времени t и среднюю наработку до первого отказа. Исходные данные для решения задачи приведены в таблице 2.

Таблица 2. Исходные данные для задачи 2

№ вар	N	, 1/час	t, час
18	189000	1,4*10-6	2

Решение

Вероятность безотказной работы P( t ):

P( t ) = e^-с*t ,

Где, _>с> – средняя интенсивность отказов;

_>с> = N*_>cp> ,

_>с> = 189000*1,4*10^-6 = 0,2646;

P( t ) = е ^-0,2646*2 = 0,589076.

Средняя наработка до первого отказа Т_>ср>:

Т_>ср> = 1 / _>с>

Т_>ср> = 1 / 0,2646= 3,779289.

Задание №3

Пусть время работы элемента до отказа подчинено экспоненциальному закону распределения с параметром . Требуется вычислить количественные характеристики надежности элемента при значение t. Построить графики зависимости от t. Исходные данные для решения задачи приведены в таблице 3.

Таблица 3. Исходные данные для задачи 3

№ варианта
18	1,4*10-6	400	500	600

Решение

Вероятность безотказной работы P( t ):

P( t ) = e^-*t

P( t_>1> ) = е ^{– 0,0000014*400} = 0,999440157;

P( t_>2> ) = е ^{– 0,0000014*500} = 0,999300245;

P( t_>3> ) = е ^{– 0,0000014*600} = 0,999160353.

Рис.1. График зависимости вероятности безотказной работы от времени

Число отказов a( t ):

a( t ) =  * e ^{-  * t}

a( t_>1> ) = 0,0000014 * е ^{– 0,0000014*400} =0,0000013992;

a( t_>2> ) = 0,0000014 * е ^{– 0,0000014*500} = 0,0000013990;

a( t_>3> ) = 0,0000014 * е ^{– 0,0000014*600} = 0,0000013988.

Рис.2. График зависимости числа отказов от времени

Средняя наработка до первого отказа T_>cp>:

T_>cp> = 1 / 

T_>cp> = 1 / 0,0000014 = 714285,7143.

Задание №4

Время работы изделия до отказа подчиняется закону распределения Релея. Требуется вычислить количественные характеристики для t час, если параметр распределения  час. Исходные данные для решения задачи приведены в таблице 5.

Таблица 5. Исходные данные для задачи 4 (вариант 11-20)

№ варианта	
18	1000	600	650	700

Решение

Вероятность безотказной работы Р(t):

= 0,8352702114;

= 0,8095716487;

= 0,7827045382.

Частота отказов (плотность распределения) а(t):

= 0,0005011621;

= 0,0005262216;

= 0,0005478932.

Интенсивность отказов (t):

= 0,00060;

= 0,00065;

= 0,00070.

Средняя наработка до первого отказа Тср:

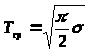= 1253,296.

Задание №5

За время испытаний по плану [n, Б, t_>0>] отказало d устройств, причем отказавшие устройства проработали до выхода из строя соответственно t_>1>-t_>n> час. Требуется определить оценку и двусторонний доверительный интервал для . Исходные данные для решения задачи приведены в таблице 8.

Таблица 8. Исходные данные для задачи 5 (вариант 11-20)

№ варианта	n	t>0>	d	t>1>-t>n>
18	70	500	5	150, 200, 300, 350, 450	0,8

Решение

Суммарная наработка :

= 33950;

Оценка интенсивности отказов :

= 0,000147275;

Верхняя граница :

0,000268041;

Нижняя граница :

= 0,00013947.

Двусторонний доверительный интервал: [0,00013947; 0,000268041].

Список литературы

Голинкевич Т.А. Прикладная теория надежности. Учебник для вузов. - М.: Высшая школа, 1985.

Боэм Б., Браун Дж., Каспар Х. И др. Характеристики качества программного обеспечения/Пер. с англ. Е. К. Масловского.- М.: Мир, 1981 – 208 с., ил.

Надежность и эффективность АСУ. Заренин Ю. Г., Збырко М. Д., Креденцер Б. П., Свистельник А. А., Яценко В. П. “Техника”, 1975, 368 стр.