Проектирование системы оптимального корректирующего устройства

ОГЛАВЛЕНИЕ

введение

1. СИНТЕЗ ЛИНЕЙНОЙ СИСТЕМЫ

1.1 Анализ исходной системы

1.2 Анализ системы с пропорциональным регулятором

1.2.1 Определение коэффициента усиления пропорционального регулятора

1.2.2 Проверка устойчивости замкнутой системы

1.2.3 Определение показателей качества

1.2.4 Анализ системы на соответствие ТЗ

1.3 Синтез регулятора

1.4 Анализ скорректированной системы

1.4.1 Построение частотных характеристик, определение устойчивости системы

1.4.2 Определение частотных ПК, запасов устойчивости, критического коэффициента усиления

1.4.3 Определение оценок прямых ПК

1.4.4 Определение корневых оценок прямых ПК

1.4.5 Оценка точности системы

2. ОТРАБОТКА ТИПОВЫХ ВХОДНЫХ СИГНАЛОВ

2.1 Единичный ступенчатый сигнал

2.1.1 Начальные и конечные значения переходных функций по передаточным функциям системы

2.1.2 Переходные функций системы, прямые ПК

2.1.3 Сравнение начальных и установившихся значений переходных функций

2.1.4 Определим величину Y_>0> ступенчатого сигнала, при котором система работает в зоне линейности УМ

2.2 Сигнал с постоянной скоростью

2.3. Гармонический сигнал

2.3.1 Определение частоты ω_>0>

2.3.2 Реакция системы на гармонический входной сигнал

2.3.3 Определение амплитудно-фазовых искажений

3. ОБЛАСТЬ УСТОЙЧИВОСТИ

4. АНАЛИЗ СИСТЕМЫ С УЧЕТОМ НЕЛИНЕЙНОСТИ УМ

4.1 Отработка ступенчатых сигналов

4.2 Определение автоколебаний в замкнутой системе

4.3 Отработка гармонических сигналов

ЗАКЛЮЧЕНИЕ

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

введение

В курсовой работе рассматривается замкнутая, одномерная, стационарная, непрерывная, следящая система с частично заданной структурой, то есть большинство ее элементов уже выбраны в соответствии с принятым принципом управления, функциональным назначением и условиями согласования с объектом управления. Система является нелинейной, однако анализ проводится как с учетом, так и без учета нелинейностей ее отдельных элементов.

При проектировании системы с частично заданной структурой основной проблемой является синтез линейной системы, т.е. определение параметров корректирующего устройства, обеспечивающего заданные требования к качеству регулирования.

В широком смысле выбор оптимального корректирующего устройства осуществляется на основе требований к массе, габаритным размерам, стоимости и других параметров, определяемых условиями эксплуатации. В более узком смысле, необходимо обеспечить качество системы в установившемся и в переходном режимах.

Для рассматриваемой системы, кроме обеспечения заданных требований, необходимо выполнить некоторые ограничения:

ограничения на коэффициент усиления: его увеличение может неблагоприятно сказаться на возрастании влияния помех, что вызывает проблемы при конструировании и наладке системы;

ограничения на положение высокочастотных асимптот логарифмической амплитудной характеристики: желательно иметь больший наклон асимптот;

ограничения на порядок модели корректирующего устройства: не выше второго порядка;

ограничения на величину частоты среза: ее уменьшение неблагоприятно сказывается на быстродействии системы.

1. СИНТЕЗ ЛИНЕЙНОЙ СИСТЕМЫ

1.1 Анализ исходной системы

Составим функциональную схему замкнутой системы. Система содержит последовательно включенные в прямой цепи: усилитель мощности (УМ) и объект управления (ОУ), в цепи обратной связи: датчик обратной связи (ДОС), связанный с ОУ при помощи кинематической связи (КС). Схема показана на рис. 1.1.

Рис. 1.1. Функциональная схема исходной системы

Составим структурную схему исходной системы. УМ предполагается безынерционным, но с ограниченной зоной линейности . В КС между ОУ и ДОС присутствует люфт (зазор) величиной 2∆. Схема изображена на рис. 1.2.

Рис. 1.2. Структурная схема исходной системы

Проведем линеаризацию исходной системы. Для этого необходимо пренебречь наличием нелинейных эффектов, то есть считать, что УМ имеет неограниченную зону нелинейности, зазор (люфт) в КС отсутствует, а коэффициент передачи равен единице.

Рассчитаем коэффициент УМ:

В техническом задании (ТЗ) коэффициент передачи датчика угла имеет размерность В/град. Для согласования размерностей в системе необходимо привести к размерности В/рад. Для этого введем коэффициент согласования град/рад:

В/рад.

Структурная схема линеаризованной системы в общем виде изображена на рис. 1.3, с числовыми параметрами на рис. 1.4.

Рис. 1.3. Структурная схема линеаризованной системы в общем виде

Рис. 1.4. Структурная схема линеаризованной системы с числовыми параметрами

Передаточная функция разомкнутой системы (ПФ РС):

Проведем анализ устойчивости исходной системы по алгебраическому критерию Гурвица [1, §6.2]. Для этого запишем характеристическое уравнение замкнутой системы (ХУ ЗС):

; ; ; ; .

Все коэффициенты ХУ ЗС положительны (), следовательно, необходимое условие устойчивости выполняется.

Проверим достаточное условие устойчивости. Для этого все n определителей Гурвица, где n – порядок системы, должны быть положительны. Составим определители для системы четвертого порядка:

Все определители положительны, следовательно, исходная система устойчива.

Проведем анализ системы на соответствие требованиям ТЗ.

1. Для определения амплитудно-фазовых искажений запишем передаточную функцию замкнутой системы (ПФ ЗС) по выходу ДОС, а также выражения для логарифмических частотных характеристик (ЛАЧХ и ЛФЧХ):

Заданные в ТЗ и рассчитанные значения амплитудно-фазовых искажений приведены в табл. 1.1.

Таблица 1.1

, Гц	0…0,15	0,15…0,5	0,5… 1,3
, с^-1	0,942	3,142	8,168
Заданные значения	, дБ	0,1	0,4	2,5
, град	3	5	16
Расчетные значения	, дБ	0,025	0,294	2,354
, град	8,57	28,68	73,35

2. Для определения величины показателя колебательности системы [4, §4.2] запишем выражение амплитудной частотной характеристики замкнутой системы (АЧХ ЗС) по выходу ДОС и построим график (рис. 1.5):

Рис. 1.5. АЧХ замкнутой системы

Показатель колебательности определяется по формуле:

где − максимальное значение АЧХ ЗC;

− начальное значение АЧХ ЗC.

Исходя из требований ТЗ, показатель колебательности не должен превышать 1,25.

Вывод: исходная система не соответствует требованиям ТЗ, так как амплитудно-фазовые искажения превышают допустимые значения.

1.2 Анализ системы с пропорциональным регулятором

1.2.1 Определение коэффициента усиления пропорционального регулятора

Структурная схема линеаризованной системы с пропорциональным регулятором в общем виде изображена на рис. 1.6.



Рис. 1.6. Структурная схема системы с пропорциональным регулятором

Расчет минимального коэффициента усиления разомкнутой системы оформим в виде таблицы (см. табл. 1.2).

Таблица 1.2

, Гц	0…0,15	0,15…0,5	0,5…1,3
, с^-1	0,942	3,142	8,168
_>>, дБ	0,1	0,4	2,5
ΔA_>n>=	0,011	0,045	0,25
_>>, град	3	5	16
_>>	0,0108	0,043	0,2
sin	0,052	0,087	0,276
ρ_>n>=	0,0108	0,043	0,2
	87,222	73,07	40,82

с^-1.

При построении ЛЧХ системы с пропорциональным регулятором необходимо чтобы график ЛАЧХ проходил выше так называемой запретной области. Асимптотическая ЛАЧХ системы с полученным таким образом коэффициентом будет обеспечивать данное условие. Необходимо проверить данное условие для расчетной ЛАЧХ.

Выражение для построения ЛАЧХ системы:

Воспользовавшись данными из табл. 1.2 запишем координаты запретной области и сравним их со значениями ЛАЧХ системы на тех же частотах (табл. 1.3).

Таблица 1.3

, Гц	0…0,15	0,15…0,5	0,5…1,3
, с^-1	0,942	3,142	8,168
ρ_>n>	0,0108	0,043	0,2
Координаты запретной области
	-0,026	0,497	0,912
	39,332	27,331	13,979
Значения расчетной ЛАЧХ
	39,322	28,76	19,885

Из таблицы (см. табл. 1.3) видно, что на частоте расчетная ЛАЧХ заходит в запретную область. Следовательно, ЛАЧХ необходимо поднять на 0,011 дБ. Таким образом, минимальный коэффициент усиления разомкнутой системы будет равен:

с^-1.

Коэффициент усиления пропорционального регулятора рассчитывается по формуле:

Структурная схема системы с пропорциональным регулятором с числовыми параметрами изображена на рис. 1.7.

Рис. 1.7. Структурная схема системы с пропорциональным регулятором



.2.2 Проверка устойчивости замкнутой системы

Проверим устойчивость системы по алгебраическому критерию Гурвица (см. п.1.1).

ХУ ЗС: ,

; ; ; ; .

Необходимое условие устойчивости выполняется, так как .

Проверим достаточное условие устойчивости. Для системы четвертого порядка достаточно проверить выполнение условия:

Условие выполняется, следовательно, система устойчива.

Проверим устойчивость системы по критерию Найквиста [1, §6.5, §6.6].

1. С использованием амплитудно-фазовой частотной характеристики (АФЧХ):

Запишем ПФ РС:

Для того чтобы судить об устойчивости замкнутой системы, необходимо проверить устойчивость разомкнутой системы. Для этого запишем характеристическое уравнение разомкнутой системы (ХУ РЗ) и найдем корни уравнения:

; ; ; .

Так как один из корней равен нулю (), а все остальные корни с отрицательными вещественными частями (левые), то можно сделать вывод, что разомкнутая система находится на апериодической границе устойчивости.

Далее необходимо построить АФЧХ разомкнутой системы (годограф Найквиста). Запишем выражение для построения АФЧХ и выделим действительную и мнимую части:

Задаваясь различными значениями ω в пределах от нуля до бесконечности, построим годограф Найквиста (рис. 1.8) по характерным точкам (табл. 1.4):

Таблица 1.4

ω
0	-5,146	-∞
46,7	-0,7	0
290,3	0	0,008
	0	0

Рис. 1.8. Годограф Найквиста

Так как годограф Найквиста, дополненный на участке разрыва дугой бесконечно большого радиуса, не охватывает особую точку (−1;j0), то замкнутая система устойчива.

2. С использованием ЛЧХ:

Запишем выражения и построим ЛАЧХ и ЛФЧХ (рис. 1.9):

Рис. 1.9. ЛЧХ системы

Замкнутая система устойчива, если выполняется неравенство:

где – частота среза, при которой ;

– критическая частота, при которой .

Так как неравенство выполняется, следовательно, замкнутая система устойчива.

Проверим устойчивость системы по критерию Михайлова [1, §6.3].

Запишем ХУ ЗС:

Подставим в этот полином чисто мнимое значение . При этом получим функцию Михайлова, как характеристический полином, состоящий из вещественной и мнимой части:

Задаваясь различными значениями ω в пределах от нуля до бесконечности, построим годограф Михайлова (рис. 1.10) по характерным точкам (табл. 1.5):

Таблица 1.5


0	87,336	0
38,82	0	11,7
46,424	-36,683	0
287,71	0	-10763,5
∞	∞	∞

Так как годограф системы, имеющей четвертый порядок, при изменении ω от 0 до ∞, начинается на вещественной положительной полуоси и при увеличении ω в положительном направлении последовательно проходит четыре квадранта, и при этом не обращается в 0, то можно сделать вывод, что замкнутая система устойчива.

Рис. 1.10. Годограф Михайлова (справа увеличен вблизи начала координат)

1.2.3 Определение показателей качества

1. Частота среза разомкнутой системы.

Частота среза разомкнутой системы была определена в анализе системы по критерию Найквиста с использованием ЛЧХ (см. п.1.2.2):

2. Запасы устойчивости.

Запасы устойчивости по амплитуде и по фазе определяются по формулам:

, ,

где , , и – ЛЧХ разомкнутой системы (см. п.1.2.2):

дБ, град.

3. Критический коэффициент усиления системы.

Коэффициент определим по алгебраическому критерию Гурвица (см. п.1.1).

ХУЗС: ,

; ; ; ; .

Условие нахождения системы на границе устойчивости:

4. Прямые показатели качества.

Прямые показатели качества системы определяются по графику переходной характеристики замкнутой системы по выходу ДОС [1, §8.4]. Запишем выражение и построим график (рис. 1.11):

Рис. 1.11. Переходная характеристика замкнутой системы по выходу ДОС

Перерегулирование определяется по формуле:

где h_>max>= 1,793 – максимальное значение переходной характеристики;

h_>уст>= 1 – установившееся значение переходной характеристики;

h(0) = 0 – начальное значение переходной характеристики.

Время регулирования определяется на уровне вхождения графика h(t) в интервал . Границы интервала [0,95;1,05] отмечены на рис. 1.11. Время регулирования определяем на уровне пересечения графиком h(t) нижней границы:

t_>р>= 1,136 с.

5. Показатель колебательности.

Показатель колебательности определяется по АЧХ ЗС по выходу ДОС (рис. 1.12):

Рис. 1.12. АЧХ замкнутой системы с пропорциональным регулятором

Показатель колебательности (см. п.1.1):

6. Частота среза замкнутой системы.

Частота среза замкнутой системы определяется по графику АЧХ ЗС (см. рис. 1.12) на уровне :

1.2.4 Анализ системы на соответствие ТЗ

Определим амплитудно-фазовые искажения системы с пропорциональным регулятором. Заданные и рассчитанные по формулам из п.1.1 значения приведены в табл. 1.6.

Таблица 1.6

, Гц	0…0,15	0,15…0,5	0,5… 1,3
, с^-1	0,942	3,142	8,168
Заданные значения	, дБ	0,1	0,4	2,5
, град	3	5	16
Расчетные значения	, дБ	0,005	0,052	0,361
, град	0,618	2,065	5,419

Вывод: система с пропорциональным регулятором не соответствует требованиям ТЗ, так как показатель колебательности () превышает допустимое значение ().

1.3 Синтез регулятора

Синтез системы управления – это направленный расчет, имеющий конечной целью отыскание рациональной структуры системы и установления оптимальных величин параметров ее отдельных звеньев. Более узкая цель синтеза – это определение вида параметров корректирующего устройства (КУ), которое необходимо ввести в исходную систему, для обеспечения требуемого качества ее функционирования, то есть обеспечения совокупности требований ТЗ, утвержденного заказчиком.

Существует большое количество методов синтеза систем автоматического управления. Наиболее известными и хорошо разработанными являются методы синтеза системы в частотной области.

Рассмотрим метод логарифмических частотных характеристик, используемый для синтеза минимально-фазовых систем. Процесс синтеза включает в себя следующие операции:

1. Построение ЛАЧХ исходной (располагаемой) системы.

2. Построение ЛАЧХ желаемой системы в соответствии с требованиями ТЗ.

3. Определение вида и параметров передаточной функции последовательного КУ.

4. Проверочный расчет, подтверждающий правильность проведенного синтеза.

1. Построение ЛАЧХ исходной системы.

Запишем выражение для построения ЛАЧХ исходной системы (см. п.1.1):

График ЛАЧХ исходной системы изображен на рис. 1.16.

2. Построение ЛАЧХ желаемой системы в соответствии с требованиями ТЗ.

Желаемую ЛАЧХ условно разделяют на три участка: низкочастотный, среднечастотный, высокочастотный.

Низкочастотный участок отвечает за точность системы в установившемся режиме, причем, чем шире этот участок (по оси ), тем больший диапазон частот воспроизводится системой без заметного ослабления. На этом участке ЛАЧХ должна проходить выше запретной области (см. табл. 1.3). Минимальный коэффициент усиления, обеспечивающий данное условие рассчитан в п.1.2.1:

Также необходимо чтобы желаемая ЛАЧХ проходила как можно ближе к границе запретной области, поэтому низкочастотный участок состоит из двух асимптот. Первая асимптота пересекает ось в точке и имеет наклон -20 дБ/дек. Вторая асимптота с наклоном -40 дБ/дек начинается на частоте сопряжения , которая соответствует наиболее близкому расположению асимптоты к запретной области. Точке пересечения второй асимптоты с осью соответствует базовая частота:

где 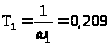– первая постоянная времени желаемой ЛАЧХ.

Среднечастотный участок определяет устойчивость, запасы устойчивости и, следовательно, качество переходных процессов. Так как в ТЗ задан показатель колебательности, то для построения данного участка необходимо воспользоваться методом Бесекерского. Постоянные времени определяются по формулам:

где ; ; .

Тогда:

, .

Таким образом, среднечастотный участок ЛАЧХ начинается на частоте

имеет наклон -20 дБ/дек, и продолжается до следующей частоты сопряжения

соответствующей высокочастотному участку.

Высокочастотный участок ЛАЧХ определяет устойчивость системы к помехам. Чтобы уменьшить влияние высокочастотных помех, необходимо иметь как можно больший наклон асимптот. Высокочастотный участок начинается на частоте и затем формируется путем последовательного увеличения наклонов на сопрягающих частотах

3. Определение вида и параметров передаточной функции последовательного КУ.

Передаточная функция полученной желаемой ЛАЧХ:

Передаточная функция последовательного КУ определяется по формуле:

Последовательное КУ включается в прямую цепь непосредственно после элемента сравнения (рис.1.13 и рис.1.14).



Рис. 1.13. Структурная схема скорректированной системы в общем виде



Рис. 1.14. Структурная схема скорректированной системы с числовыми параметрами

4. Проверочный расчет, подтверждающий правильность проведенного синтеза

Проведем анализ скорректированной системы на соответствие требованиям ТЗ.

1. Заданные в ТЗ и рассчитанные значения амплитудно-фазовых искажений (см. п.1.1) приведены в табл. 1.7.

Таблица 1.7

, Гц	0…0,15	0,15…0,5	0,5… 1,3
, с^-1	0,942	3,142	8,168
Заданные значения	, дБ	0,1	0,4	2,5
, град	3	5	16
Расчетные значения	, дБ	0,009	0,095	0,417
, град	0,624	2,262	7,653

2. Для определения величины показателя колебательности системы запишем выражение АЧХ ЗС по выходу ДОС и построим график (рис. 1.15):

Рис. 1.15. АЧХ замкнутой системы

Показатель колебательности (см. п.1.1):

Исходя из требований, показатель колебательности не должен превышать 1,25.

Соответствие показателя колебательности требованиям ТЗ также можно определить по графику ЛФЧХ скорректированной разомкнутой системы. Для этого на графике ЛФЧХ необходимо построить запретную зону [2, §7.5]. В диапазоне частот:

график ЛФЧХ не должен заходить в зону, ограниченную прямой -180^ и кривой -180^+, где

; ; .

На рис. 1.16 видно что график ЛФЧХ не заходит в эту запретную зону, следовательно, показатель колебательности не превышает заданного в ТЗ значения.

Вывод: корректирующее устройство рассчитано верно, скорректированная система соответствует требованиям ТЗ.

1.4 Анализ скорректированной системы

1.4.1 Построение частотных характеристик, определение устойчивости системы

Запишем выражения для построения ЛАЧХ и ЛФЧХ разомкнутой системы:

Графики ЛАЧХ и ЛФЧХ построены на рис. 1.16.

Определим устойчивость системы по графикам ЛАЧХ и ЛФЧХ по критерию Найквиста (см. п.1.2.2):

Так как неравенство выполняется, то замкнутая система устойчива.

Из рис. 1.16 видно, что частота среза скорректированной системы больше чем у системы с пропорциональным регулятором, что благоприятно сказывается на качестве переходных процессов. Также видно, что график ЛФЧХ системы с пропорциональным регулятором заходит в запретную зону, следовательно, не соответствует требованиям к показателю колебательности.

Запишем выражение для построения АФЧХ разомкнутой системы (годограф Найквиста):

Построим годограф Найквиста (рис. 1.17) по характерным точкам (табл. 1.8):

Таблица 1.8

ω
0	-9,78	-∞
530,8	0	0,006
152,4	-0,178	0
	0	0

Рис. 1.17. АФЧХ разомкнутой системы

Из рис. 1.17 видно, что годограф скорректированной системы наиболее удален от особой точки (−1;j0), следовательно, имеет наибольшие запасы устойчивости в отличие от системы с пропорциональным регулятором.

Построим годограф Михайлова замкнутой системы (см. п.1.2.2).

Годограф Михайлова изображен на рис. 1.18 по характерным точкам (табл. 1.9):

Таблица 1.9

ω
0	87,336	0
20,037	0	190,39
64,71	-687,1	0
158,94	0	-7673
534,97		0

Так как годограф системы, имеющей пятый порядок, при изменении ω от 0 до ∞, начинается на вещественной положительной полуоси и при увеличении ω в положительном направлении последовательно проходит пять квадрантов, и при этом не обращается в 0, то можно сделать вывод, что система устойчива.

Рис. 1.18. Годограф Михайлова (справа увеличен в начале координат)

1.4.2 Определение частотных ПК, запасов устойчивости, критического коэффициента усиления

1. Частота среза разомкнутой системы.

Частота среза разомкнутой системы была определена в п.1.4.1:

2. Запасы устойчивости.

Из п.1.4.1: , ,

дБ, град.

3. Критический коэффициент усиления системы.

Коэффициент определим аналогично п.1.2.3.

ХУ ЗС: ,

; ; ; ; ;

Условие нахождения системы на границе устойчивости:

с^-1.

4. Показатель колебательности.

Из п.1.3: .

5. Частота среза замкнутой системы.

Частота среза замкнутой системы определяется по графику АЧХ ЗС (рис. 1.15) на уровне :

Сравним показатели качества системы с пропорциональным регулятором и скорректированной системы (табл. 1.10).

Таблица 1.10

	С пропорциональным регулятором	Скорректированная система
, разомкнутой системы	38,639	43,67
, замкнутой системы	54,961	55,807
,	46,424	152,356
, дБ	3,038	14,958
, град.	7,813	54,935
	7,721	1,113
,	123,904	490,257

1.4.3 Определение оценок прямых ПК

Выражение для построения вещественной частотной характеристики (ВЧХ) системы по выходу ДОС (рис. 1.19):

Рис. 1.19. ВЧХ по выходу ДОС

По графику ВЧХ замкнутой системы можно оценить прямые ПК [1, §8.5].

1. Оценка перерегулирования.

В данном случае график имеет положительный максимум и отрицательный минимум. Тогда верхняя оценка перерегулирования:

где – положительный максимум ВЧХ;

– отрицательный минимум ВЧХ;

– начальное значение ВЧХ.

Следовательно: .

2. Оценка времени регулирования.

Время регулирования находится в пределах:

где – частота положительности.

Тогда: .

Выражения для построения ЛАЧХ и ЛФЧХ замкнутой системы по выходу ДОС (рис. 1.20):

Рис. 1.20. ЛЧХ замкнутой системы по выходу ДОС

1.4.4 Определение корневых оценок прямых ПК

Оценить прямые ПК можно также по корням ПФ ЗС:

Нули передаточной функции – корни полинома числителя:

Полюса передаточной функции – корни полинома знаменателя:

Изобразим нули и полюса на комплексной плоскости (рис. 1.21).

Рис. 1.21. АФЧХ разомкнутой системы

Чтобы оценить прямые ПК необходимо определить доминирующие полюса. Близко расположенные нуль и полюс компенсируют друг друга. Полюс, скомпенсированный нулем, не участвует в оценке прямых ПК. Если выполняется хотя бы одно из неравенств критерия «близости», то нуль компенсирует полюс:

Проверим выполнение критерия «близости» нуля и полюса :

Ни одно из неравенств не выполняется, следовательно, близко расположенных нулей и полюсов нет.

Доминирующим является вещественный полюс , так как он наиболее близко расположен к мнимой оси. Из этого следует, что система имеет апериодическую степень устойчивости , равную величине вещественной части доминирующего полюса ().

1. Оценка времени регулирования.

Верхняя оценка времени регулирования определяется по формуле:

где ; .

Тогда: , .

2. Оценка перерегулирования.

Нижняя оценка перерегулирования:

где – колебательность;

– наиболее близкие к мнимой оси комплексно-сопряженные корни.

Тогда: .

1.4.5 Оценка точности системы

Точность системы характеризует величина установившейся ошибки, для определения которой воспользуемся методом коэффициентов ошибок.

Запишем ПФ ЗС по ошибке:

Данную функцию можно разложить в ряд Тейлора по степеням s:

где – коэффициенты ошибок.

Переходя от изображения к оригиналу, выражение для установившейся ошибки можно представить в виде:

( 1)

Известно два способа, определения коэффициентов ошибки :

1. Вычисление производных соответствующих порядков ПФ ЗС в точке s=0:

2. Деление уголком полинома числителя ПФ ЗС на полином знаменателя. Для этого необходимо коэффициенты числителя и знаменателя записать в порядке возрастания степени s, начиная со свободного члена:

Делить весь полином числителя нет необходимости, так как необходимо узнать только первые три коэффициента ошибки:

, , .

В данном случае система астатическая первого порядка, так как в прямой цепи системы имеется интегрирующее звено, а также . С увеличением коэффициента усиления разомкнутой системы К_>р> значения коэффициентов ошибки и уменьшаются, однако увеличение К_>р>приводит к ухудшению показателей качества переходной характеристики, а при К_>р>больше граничного значения система оказывается неустойчивой.

Рассчитаем установившуюся ошибку для заданных в ТЗ сигналов:

1. Единичное ступенчатое воздействие . Ошибку определим по формуле (1):

2. Сигнал с постоянной скоростью . По формуле (1):

3. Гармонический сигнал , где (из п.2.3).

Ошибка системы определяется выражением вида:

где – амплитуда;

– сдвиг фаз.

Тогда установившаяся ошибка системы:

2. ОТРАБОТКА ТИПОВЫХ ВХОДНЫХ СИГНАЛОВ

2.1 Единичный ступенчатый сигнал

2.1.1 Начальные и конечные значения переходных функций по передаточным функциям системы

ПФ ЗС по выходу системы:

ПФ ЗС по выходу ДОС:

ПФ ЗС по выходу УМ:

Начальное и конечное значение переходной функции , зная ПФ ЗС , можно рассчитать исходя из свойств преобразования Лапласа [3, §2.2]:

Рассчитанные начальные и конечные значения переходных функций ( и ) по всем выходам приведены в табл. 2.1.

Таблица 2.1


0	0	4415,98
0,0873	1	0

Конечное значение переходной функции по выходу системы определяется как отношение коэффициентов в прямой цепи системы (, , ) к коэффициенту усиления разомкнутой системы .

Конечное значение переходной функции по выходу ДОС от величин параметров системы не зависит.

Начальное значение переходной функции по выходу УМ зависит от коэффициентов и , а также от всех постоянных времени системы.

2.1.2 Переходные функций системы, прямые ПК

Построим переходную характеристику системы (рис. 2.1) по выходу ОУ (по выходу системы). Выражение для построения:

Рис. 2.1. Переходная характеристика системы по выходу системы

Определим прямые ПК по выходу системы (см. п.1.2.3).

Перерегулирование:

где h_>max>= 0,101;

h_>уст>= 0,0873;

h(0) = 0.

Границы интервала для установившегося значения [0,083;0,092].

Время регулирования: t_>р>= 0,104 с.

Построим переходную характеристику системы (рис. 2.2) по выходу ДОС. Выражение для построения:

Рис. 2.2. Переходная характеристика системы по выходу ДОС

Определим прямые ПК (см. п.1.2.3).

Перерегулирование:

где h_>max>= 1,151;

h_>уст>= 1;

h(0) = 0:

Границы интервала для установившегося значения [0,95;1,05].

Время регулирования: t_>р>= 0,106 с.

Полученные прямые ПК по выходу системы и по выходу ДОС, а также оценки ПК, найденные в пп.1.4.3 и 1.4.4 занесем в таблицу (табл. 2.2).

Таблица 2.2

	По выходу системы	По выходу ДОС	Оценки прямых ПК
Нижняя граница	Верхняя граница
	15,4	15,14	6,65	35
t_>р>, с	0,104	0,106	0,053	0,292

ПК найденные по выходу системы и по выходу ДОС различаются незначительно. Это объясняется тем, что в обратной связи имеется малая постоянная времени, практически не влияющая на динамические свойства системы.

Из таблицы также видно, что полученные ПК находятся в пределах нижней и верхней границ, найденных в пп.1.4.3 и 1.4.4.

2.1.3 Сравнение начальных и установившихся значений переходных функций

Определим начальное и установившееся значение переходной функций по выходу УМ:

, .

Начальные и установившиеся значения переходных функций, рассчитанные в пп.2.1.1 и 2.1.2, совпадают. Эти значения приведены в табл. 2.3.

Таблица 2.3


0	0	0	0	4415,98	4415,98
0,0873	0,0873	1	1	0	0

2.1.4 Определим величину Y_>0> ступенчатого сигнала, при котором система работает в зоне линейности УМ

Допустимая величина ступенчатого сигнала Y_>0>, при котором система работает в зоне линейности УМ:

где B – максимальное выходное напряжение УМ;

– максимальное значение выходного сигнала УМ на единичное ступенчатое воздействие.

Тогда:

2.2 Сигнал с постоянной скоростью

Воздействие в виде сигнала с постоянной скоростью имеет вид:

Выражение для построения ошибки системы при обработке такого сигнала имеет вид:

где – ПФ ЗС (из п.1.4.4);

– изображение по Лапласу сигнала с постоянной скоростью.

Тогда:

Значение установившейся составляющей ошибки было вычислено в п.1.4.5:

В.

График ошибки и ее установившейся составляющей изображен на рис. 2.3.

Рис. 2.3. График ошибки и ее установившейся составляющей при подаче сигнала с постоянной скоростью

Вынужденный режим устанавливается на уровне вхождения графика в интервал .

Границы интервала [0,098;0,108].

Время установления вынужденного режима:

t_>в>= 0,313 с.

Время установления вынужденного режима при воздействии сигнала с постоянной скоростью (t_>в>= 0,313 с) больше времени регулирования (t_>р>= 0,106 с).

2.3 Гармонический сигнал

2.3.1 Определение частоты

Запишем выражение для АЧХ по выходу УМ и построим график (рис. 2.4):

Рис. 2.4. АЧХ по выходу УМ

По графику АЧХ системы по выходу УМ определим такую частоту входного гармонического сигнала , для которой амплитуда установившихся колебаний равна =110 В при амплитуде входного сигнала :

2.3.2 Реакция системы на гармонический входной сигнал

Воздействие в виде гармонического сигнала имеет вид:

Выражение для построения реакции системы по выходу ДОС при обработке такого сигнала имеет вид:

где – ПФ ЗС по выходу ДОС;

– изображение по Лапласу гармонического сигнала.

Запишем выражение реакции системы на гармонический сигнал и построим график (рис. 2.5):

Рис. 2.5. График реакции системы на гармонический входной сигнал

2.3.3 Определение амплитудно-фазовых искажений

Амплитудные искажения определяются по формуле:

где – максимальное значение амплитуды выходного сигнала;

– максимальное значение амплитуды входного сигнала.

По графику реакции системы на гармонический сигнал (рис. 2.5):

Тогда амплитудные искажения:

дБ.

Фазовые искажения определяются по формуле:

где – временной сдвиг между входным и выходным сигналом.

По графику реакции системы на гармонический сигнал (рис. 2.5):

Тогда фазовые искажения:

град.

Определим амплитудно-фазовые искажения по частотным характеристикам (см. п.1.1) на частоте :

дБ,

град.

Полученные значения занесем в таблицу (табл. 2.4).

Таблица 2.4

	При отработки гармонического сигнала	По частотным характеристикам
, дБ	0,701	0,698
, град	16,23	15,93

Из табл. 2.4 видно, что рассчитанные разными способами амплитудно-фазовые искажения практически совпадают. Различие можно объяснить округлением значений при расчетах.

3. ОБЛАСТЬ УСТОЙЧИВОСТИ

Рассчитаем и построим область устойчивости с использованием критерия Гурвица (см. п.1.1) на плоскости параметров «постоянная времени корректирующего устройства – коэффициент усиления разомкнутой системы ».

ХУ ЗС: ,

; ; ; ; ; .

Необходимое условие устойчивости , .

Достаточное условие нахождения системы пятого порядка на границе устойчивости:

Таким образом, достаточное условие нахождения системы на границе устойчивости:

Область устойчивости изображена на рис. 3.1.

Рис. 3.1. Область устойчивости в области параметров К

Точка А[0,109;87,336], соответствующая параметрам системы и , удалена от границы и находится внутри области устойчивости, что соответствует большим запасам устойчивости системы.

Точка В[0,109;490,257], соответствующая параметрам системы и , находится на границе устойчивости и совпадает с найденным в п.1.4.2 критическим коэффициентом усиления .

4. АНАЛИЗ СИСТЕМЫ С УЧЕТОМ НЕЛИНЕЙНОСТИ УМ

4.1 Отработка ступенчатых сигналов

Исследуем систему с учетом нелинейности УМ (рис. 4.1 и рис. 4.2).



Рис. 4.1. Структурная схема системы с учетом нелинейности УМ в общем виде



U_>дос>

Рис. 4.2. Структурная схема системы с учетом нелинейности УМ с числовыми параметрами

Построим реакции системы по выходу УМ (рис. 4.3), скорости выхода системы (рис. 4.4) и по выходу ДОС (рис. 4.5) на ступенчатый входной сигнал величины Y_>0>, 2Y_>0>, 5Y_>0> и 1 В, где В. Построение выполнено в программе VisSim.

Рис. 4.3. Реакции системы по выходу УМ на ступенчатый сигнал

Рис. 4.4. Реакции системы по выходу системы на ступенчатый сигнал

Рис. 4.5. Реакции системы по выходу ДОС на ступенчатый сигнал

По построенным реакциям (рис. 4.4 и рис. 4.5) найдем прямые ПК по выходу системы и выходу ДОС по формулам из п. 2.1.2 и сравним их с ПК, полученными в п. 2.1. Результаты занесем в таблицы (табл. 4.1 и табл. 4.2).

Таблица 4.1

ПК по выходу системы

	Без учета нелинейности	С учетом нелинейности
В	В	В	1 В
	15,4	15,517	8,343	5,307	9,759
t_>р>, с	0,104	0,102	0,095	0,209	0,31

Таблица 4.2

ПК по выходу ДОС

	Без учета нелинейности	С учетом нелинейности
В	В	В	1 В
	15,14	15,36	8,3	5,034	9,76
t_>р>, с	0,106	0,106	0,097	0,19	0,309

При подаче на вход ступенчатого воздействия В, значения прямых ПК близки значениям ПК линейной системы, так как при таком воздействии система работает в зоне линейности УМ. При воздействиях 2Y_>0> и 5Y_>0>время регулирования увеличивается, следовательно, ухудшается быстродействие системы, но перерегулирование уменьшается. Этот процесс аналогичен уменьшению коэффициента усиления разомкнутой системы, при котором увеличивается время регулирования и уменьшается показатель перерегулирования.

4.2 Определение автоколебаний в замкнутой системе

Для определения возможности возникновения автоколебаний в замкнутой системе воспользуемся частотным методом анализа симметричных автоколебаний. Однако прежде чем использовать этот метод необходимо линеаризовать нелинейный элемент с помощью метода гармонической линеаризации.

Согласно методу гармонической линеаризации нелинейный элемент, описываемый уравнением , заменяется на эквивалентный линейный. Условием эквивалентности является совпадение линейного и нелинейного элементов при обработке одинаковых гармонических сигналов .

Таким образом, эквивалентный линейный элемент описывается уравнением:

где – эквивалентный комплексный коэффициент усиления (ЭККУ);

– амплитуда автоколебаний.

ЭККУ можно представить в виде:

где коэффициенты гармонической линеаризации.

В данном случае рассматривается нелинейный элемент типа «насыщение», описываемый однозначной нелинейностью. Для всех однозначных нелинейностей . Следовательно, ЭККУ примет вид:

Линейная часть системы такова, что выполняется гипотеза фильтра, то есть график ЛАЧХ линейной части системы состоит из асимптот с наклоном не менее -20 дБ/дек. Следовательно, выходной сигнал нелинейного элемента раскладывается в ряд Фурье и рассматривается только первая гармоника разложения.

Таким образом:

Рассчитаем ЭККУ, причем параметры нелинейности примем , , а коэффициент усиления учтем при построении годографа Найквиста:

Таким образом, ЭККУ нелинейного элемента:

Исследуем возможность возникновения автоколебаний в замкнутой системе с помощью частотного метода. Для этого на одной координатной плоскости (рис. 4.6) изобразим годограф Найквиста (АФЧХ разомкнутой системы из п.1.4.1) и годограф ЭККУ (инверсный ЭККУ взятый с обратным знаком):

Рис. 4.6. Годографы Найквиста и ЭККУ

Из рис. 4.6 видно, что годографы Найквиста и ЭККУ не пересекаются, следовательно, возможности возникновения автоколебаний в системе нет.

4.3 Отработка гармонических сигналов

Построим реакции системы с учетом насыщения в УМ по выходу УМ (рис. 4.7) и по выходу ДОС (рис. 4.8) на гармонический входной сигнал с амплитудой 1 В, 3 В и 5 В, и с частотой . Построение выполнено в программе VisSim.

Рис. 4.7. Реакции системы по выходу УМ на гармонический сигнал

Рис. 4.8. Реакции системы по выходу ДОС на гармонический сигнал

Рассчитаем амплитудно-фазовые искажения по выходу ДОС и сравним их со значениями, полученными в п.2.3.3 (табл. 4.3).

Таблица 4.3

	Без учета нелинейности	С учетом нелинейности
А = 1 В	А = 3 В	А = 5 В
, дБ	0,701	0,642	6,472	9,525
, град	16,23	16,232	85,217	102,261

При подаче на вход гармонического сигнала с амплитудой А = 1 В, система работает в зоне линейности УМ и амплитудно-фазовые искажения близки значениям полученным при исследовании линейной системы. При увеличении амплитуды входного сигнала система работает в зоне нелинейности УМ, вследствие чего сигнал на выходе заметно искажен по амплитуде и по фазе, что заметно ухудшает работу системы.

ЗАКЛЮЧЕНИЕ

В результате проделанной работы произведен расчет корректирующего устройства, удовлетворяющего заданной совокупности требований, а также обеспечивающего рациональную структуру системы и установление оптимальных величин параметров ее отдельных звеньев.

Соответствие характеристик рассчитанной системы, требованиям технического задания приведено в табл. 4.5.

Таблица 4.5

Амплитудно-фазовые искажения
, Гц	0…0,15	0,15…0,5	0,5… 1,3
, с^-1	0,942	3,142	8,168
Заданные значения	, дБ	0,1	0,4	2,5
, град	3	5	16
Расчетные значения	, дБ	0,009	0,095	0,417
, град	0,624	2,262	7,653
Показатель колебательности
Заданное значение		1,25
Расчетное значение	1,113

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

Бесекерский, В.А. Теория систем автоматического регулирования: монография / В.А. Бесекерский, Е.П. Попов. – 3-е изд., испр. – М.: Наука, 1975. – 768 c.

Макаров, И.М. Линейные автоматические системы: учебное пособие / И.М. Макаров, Б.М. Менский. – 2-е изд., перераб. и доп. – М.: Машиностроение, 1982. – 504 c.

Зырянов, Г.В. Динамический синтез систем автоматического управления: учебное пособие / Г.В. Зырянов, А.А. Кощеев. – Челябинск: ЮУрГУ, 2001. – 40 c.

Павловская, О.О. Теория автоматического управления: учебное пособие / О.О. Павловская, Е.В. Плотникова.  Челябинск: ЮУрГУ, 2000. – 60 c.