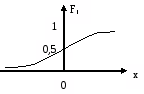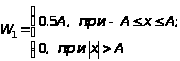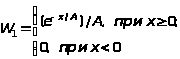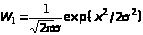Випадкові процеси та одновимірні закони розподілу ймовірностей
Випадкові процеси та одновимірні закони розподілу ймовірностей
Характер прийнятих сигналів як носіїв інформації є випадковим і заздалегідь не є відомий, тому з цього погляду сигнали треба розглядати як випадкові функції часу. Крім того, передавання інформації завжди супроводжується дією різноманітних завад та шумів, тому реальні сигнали є сумішшю корисного сигналу та завади.
Ha відміну від детермінованих сигналів, які не несуть інформації і однозначно визначають значення конкретного процесу в будь-який момент часу, перебіг випадкових сигналів передбачити неможливо. Проте, спостерігаючи за численними реалізаціями одного і того ж випадкового процесу під імовірнісним кутом зору, можна виявити певні закономірності, що характеризують цей процес, та визначити сукупність невипадкових числових характеристик, які описують його.
Математичною
моделлю випадкового сигналу є випадкова
функція. Випадкова функція будь-якого
аргументу – це функція, значення якої
при кожному значенні аргументу є
випадкове. Випадкову функцію часу
називають випадковим процесом. Випадковий
процес позначимо функцією
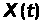 .
Спостерігаючи багаторазово за одним і
тим же випадковим процесом, що перебігає
в незмінних умовах, кожен раз отримуємо
конкретні реалізації
.
Спостерігаючи багаторазово за одним і
тим же випадковим процесом, що перебігає
в незмінних умовах, кожен раз отримуємо
конкретні реалізації
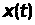 ,
не подібні одна на одну.
,
не подібні одна на одну.
Крім того, неможливо передбачити, яку саме реалізацію отримаємо при даному конкретному спостереженні. Кожне окреме спостереження називають дослідом або випробуванням.
Випадковий процес повністю характеризується нескінченно великою кількістю реалізацій, які утворюють ансамбль реалізацій. Ha основі дослідження заданого ансамблю можна визначити статистичні характеристики, властиві випадковому процесові.
Розглянемо
 реалізацій випадкового процесу
реалізацій випадкового процесу
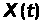 (рис. l). Сукупність миттєвих значень
випадкового процесу, заданого ансамблем
реалізацій у довільний момент часу,
називають перетином випадкового процесу.
(рис. l). Сукупність миттєвих значень
випадкового процесу, заданого ансамблем
реалізацій у довільний момент часу,
називають перетином випадкового процесу.
Ha
рис. 1 показано перетин випадкового
процесу
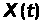 в момент
в момент
 ,
який дає змогу визначити сукупність
миттєвих значень процесу
,
який дає змогу визначити сукупність
миттєвих значень процесу
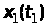 ;
;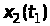 ,..
,..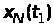 .
Ця сукупність дає можливість визначити
одновимірну функцію розподілу ймовірностей
випадкової величини
.
Ця сукупність дає можливість визначити
одновимірну функцію розподілу ймовірностей
випадкової величини
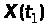 .
Для цього виділимо ті значення, які в
момент часу
.
Для цього виділимо ті значення, які в
момент часу
 задовольняють умову:
задовольняють умову:
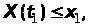 (1)
(1)
де
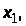 – деяке вибране значення випадкового
процесу.
– деяке вибране значення випадкового
процесу.
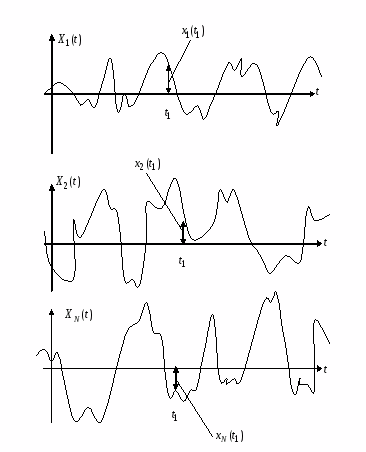
Рисунок 1 – Ансамбль реалізацій випадкового процесу
Позначимо
число цих значень як
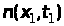 .
Відношення
.
Відношення
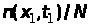 називають у теорії ймовірностей частотою
настання події. У даному разі під подією
розуміємо виконання умови (1). При
достатньо великому значенні
називають у теорії ймовірностей частотою
настання події. У даному разі під подією
розуміємо виконання умови (1). При
достатньо великому значенні
 відношення
відношення
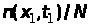 прямуватиме до постійного числа, яке
називають ймовірністю того, що при
прямуватиме до постійного числа, яке
називають ймовірністю того, що при
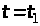 випадкова функція
випадкова функція
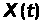 менша від значення
менша від значення
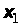 :
:
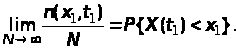 (2)
(2)
Ha
практиці при достатньо великих
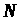 можна наближено вважати:
можна наближено вважати:
 (3)
(3)
Діючи
аналогічно для інших значень
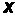 в інтервалі
в інтервалі
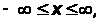 можемо побудувати одновимірну функцію
розподілу ймовірностей випадкового
процесу (рис.2):
можемо побудувати одновимірну функцію
розподілу ймовірностей випадкового
процесу (рис.2):
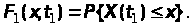 (4)
(4)
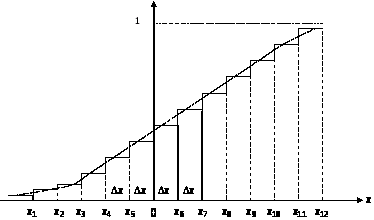
Рисунок 2 – Одновимірна функція розподілу ймовірностей випадкового процесу
Функція
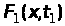 матиме ступінчастий характер у тому
разі, якщо випадковий процес набирає
дискретних значень. Якщо ж випадковий
процес змінює свої значення неперервно,
то функція
матиме ступінчастий характер у тому
разі, якщо випадковий процес набирає
дискретних значень. Якщо ж випадковий
процес змінює свої значення неперервно,
то функція
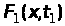 теж матиме вигляд плавної кривої.
Очевидно, що для її побудови треба
зменшувати до нуля інтервал
теж матиме вигляд плавної кривої.
Очевидно, що для її побудови треба
зменшувати до нуля інтервал
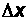 між сусідніми значеннями
між сусідніми значеннями
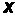 (рис.2). Зауважимо, що функція розподілу
ймовірностей є неспадаючою функцією
свого аргументу. Це випливає з її
означення.
(рис.2). Зауважимо, що функція розподілу
ймовірностей є неспадаючою функцією
свого аргументу. Це випливає з її
означення.
Тісно пов'язаною з одновимірною функцією розподілу ймовірностей випадкового процесу є одновимірна густина розподілу ймовірностей випадкового процесу, яку на основі ансамблю реалізацій наближено визначимо так:
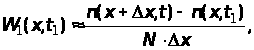 (5)
(5)
де
 – кількість реалізацій, значення яких
у момент
– кількість реалізацій, значення яких
у момент
 були менші від
були менші від
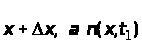 визначаємо, як і раніше.
визначаємо, як і раніше.
За такого визначення густина розподілу теж має ступінчастий вигляд, як показано нa рис.
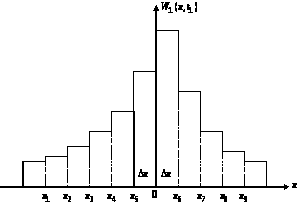
Рисунок 3 – Одновимірна густина розподілу ймовірностей
Підвищення
точності визначення густини розподілу
можна досягти зменшенням інтервалу
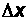 до нуля:
до нуля:
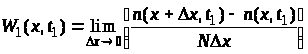 .
(6)
.
(6)
Із
(6) бачимо, що густина розподілу є похідною
по
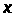 одновимірної функції розподілу.
Узагальнюючи, можемо записати:
одновимірної функції розподілу.
Узагальнюючи, можемо записати:
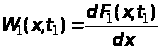 .
(7)
.
(7)
Очевидно,
що в загальному випадку графік функції
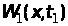 має вигляд плавної кривої (рис. 3):
має вигляд плавної кривої (рис. 3):
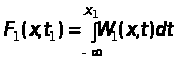 ,
(8)
,
(8)
з
якого випливає, що значення функції
розподілу ймовірностей для аргументу
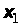 дорівнює площі під кривою густини
розподілу ймовірностей у межах від
дорівнює площі під кривою густини
розподілу ймовірностей у межах від
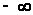 до
до
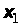 .
.
Очевидно,
що ймовірність того, що значення
випадкового процесу лежить у межах від
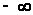 до
до
 ,
дорівнює одиниці, тобто
,
дорівнює одиниці, тобто
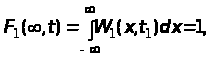 (9)
(9)
а
ймовірність того, що випадкова функція
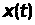 у момент
у момент
 перебуває в інтервалі між
перебуває в інтервалі між
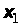 та
та
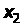 ,
дорівнює:
,
дорівнює:
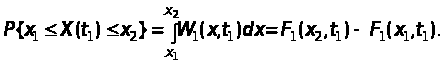 (10)
(10)
Отже,
ймовірність того, що значення випадкової
функції у момент
 перебувають у заданому інтервалі,
дорівнює різниці значень функції
розподілу ймовірностей для верхньої
та нижньої меж заданого інтервалу.
перебувають у заданому інтервалі,
дорівнює різниці значень функції
розподілу ймовірностей для верхньої
та нижньої меж заданого інтервалу.
Співвідношення (9) називають умовою нормування.
Зауважимо
також, що функції
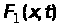 та
та
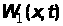 для довільних значень
для довільних значень
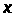 та
та
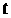 завжди приймають додатні значення.
завжди приймають додатні значення.
Часто
функцію розподілу ймовірностей
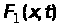 називають інтегральним законом розподілу,
а густину розподілу ймовірностей –
диференціальним законом розподілу
ймовірностей.
називають інтегральним законом розподілу,
а густину розподілу ймовірностей –
диференціальним законом розподілу
ймовірностей.
Функції
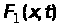 та
та
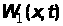 статистично
повністю характеризують значення
випадкової функції
статистично
повністю характеризують значення
випадкової функції
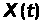 у заданий момент часу
у заданий момент часу
 і тому їх називають одновимірними. Ці
функції є найпростішими характеристиками
випадкового процесу, оскільки вони
дають уявлення про процес лише в окремі
фіксовані моменти часу.
і тому їх називають одновимірними. Ці
функції є найпростішими характеристиками
випадкового процесу, оскільки вони
дають уявлення про процес лише в окремі
фіксовані моменти часу.
У таблицях 1 та 2. подані деякі найбільш поширені одновимірні закони розподілу ймовірностей випадкових процесів.
Таблиця 1 – Типові
одновимірні функції розподілу ймовірностей
випадкових процесів

|
Назва закону |
Одновимірна
функція розподілу
|
Графік
функції
|
|
1 |
2 |
3 |
|
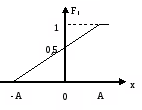
Рівномірний |
|
|
|
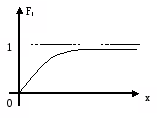
Експоненційний |
|
|
|
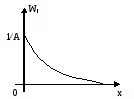
Нормальний (закон Гауса) |
|
|
Таблиця
2 – Типові одновимірні функції розподілу
ймовірностей випадкових процесів
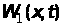
|
Назва закону |
Одновимірна
густина розподілу
|
Графік
функції
|
|
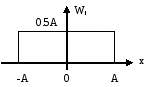
Рівномірний |
|
|
|
Експоненційний |
|
|
|
Нормальний (закон Гауса) |
|
|
Проходження сигналів в електронних колах супроводжується різноманітними перетвореннями характеристик сигналів. У випадкових сигналів можуть змінюватися закони їх розподілу, аналітичний розрахунок часто дуже складний.
Виявляється, що значно простішим є завдання розрахунку певних числових характеристик законів розподілу, які можна визначити на основі нескладних експериментів. У багатьох випадках точність розрахунків, що забезпечують згадані числові характеристики, цілком задовільна для потреб практики. Такими числовими характеристиками є моменти випадкової величини. Вони є детермінованими числами.
Момент
 -го
порядку
-го
порядку
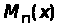 неперервної випадкової величини
неперервної випадкової величини
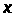 визначають за формулою:
визначають за формулою:
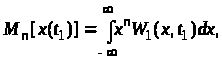 (11)
(11)
де
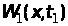 – одновимірна густина розподілу
ймовірностей випадкової величини
– одновимірна густина розподілу
ймовірностей випадкової величини
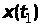 .
.
Момент першого порядку
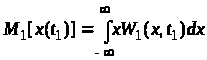 (12)
(12)
називають математичним сподіванням або середнім значенням випадкової величини.
Зауважимо,
що згідно з (12) усереднення випадкової
величини
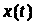 проводиться по ансамблю із
проводиться по ансамблю із
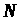 реалізацій випадкового процесу.
Статистичне визначення його середнього
значення у перетині в момент часу
реалізацій випадкового процесу.
Статистичне визначення його середнього
значення у перетині в момент часу
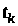 здійснюємо за формулою:
здійснюємо за формулою:
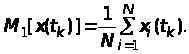 (13)
(13)
Для прикладу визначимо моменти першого та другого порядку для рівномірного та експоненційного закону розподілу ймовірностей (табл. 1 та 2).
Рівномірний закон розподілу.
Математичне сподівання
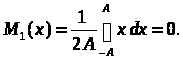 (14)
(14)
Момент другого порядку
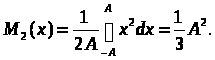 (15)
(15)
Експоненційний закон розподілу.
Математичне сподівання
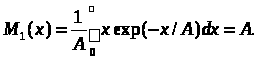 (16)
(16)
Момент другого порядку
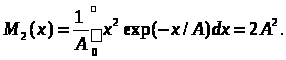 (17)
(17)
Взаємозв'язок між формою закону розподілу ймовірностей та його числовими характеристиками стає більш наочним при використанні поняття центрованої випадкової величини. Випадкова величина називається центрованою, якщо її середнє значення дорівнює нулеві.
Отже,
випадкова величина
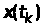 центрується відніманням від неї
середнього значення
центрується відніманням від неї
середнього значення
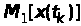 :
:
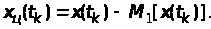 (18)
(18)
Із
(18) випливає, що центрування випадкової
величини є рівнозначне зміщенню початку
координат на графіку одновимірної
густини розподілу ймовірностей
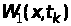 на величину
на величину
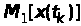 вздовж осі абсцис і не приводить до
деформації закону розподілу. Сказане
ілюструє рис. 4.
вздовж осі абсцис і не приводить до
деформації закону розподілу. Сказане
ілюструє рис. 4.
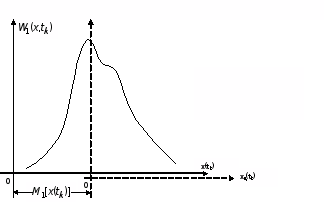
Рисунок 4 – Центрування випадкової величини
Ha відміну від початкових моментів, які визначають за формулою (11), моменти центрованої величини називають центральними моментами.
Центральний
момент
 ro порядку визначають за формулою:
ro порядку визначають за формулою:
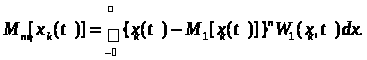 (19)
(19)
Центральний момент першого порядку центрованої випадкової величини завжди дорівнює нулеві за означенням:
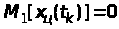 .
(20)
.
(20)
Центральний момент другого порядку
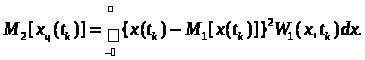 (21)
(21)
Із (21) випливає, що другий центральний момент можна визначити через початкові моменти таким чином:
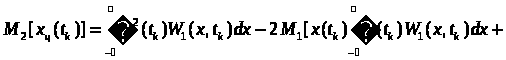
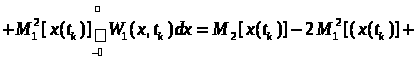
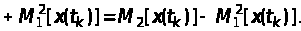 (22)
(22)
Цей
момент характеризує розсіювання можливих
значень випадкової величини
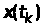 відносно її середнього значення і
називається дисперсією. Стосовно
електричних сигналів дисперсія
характеризує потужність відхилень
випадкової величини від середнього
значення, яка виділяється на навантаженні
в 1 Ом.
відносно її середнього значення і
називається дисперсією. Стосовно
електричних сигналів дисперсія
характеризує потужність відхилень
випадкової величини від середнього
значення, яка виділяється на навантаженні
в 1 Ом.
Часто використовують таке позначення дисперсії:
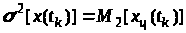 .
(23)
.
(23)
Величину
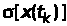 ,
що дорівнює додатному значенню кореня
квадратного з центрального моменту
другого порядку, називають середнім
квадратичним відхиленням випадкової
величини
,
що дорівнює додатному значенню кореня
квадратного з центрального моменту
другого порядку, називають середнім
квадратичним відхиленням випадкової
величини
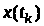 .
.
Розмірність
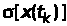 збігається із розмірністю випадкової
величини
збігається із розмірністю випадкової
величини
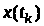 і тому її можна використовувати для
оцінювання ширини кривої густини
розподілу ймовірностей: чим більше
значення
і тому її можна використовувати для
оцінювання ширини кривої густини
розподілу ймовірностей: чим більше
значення
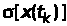 ,
тим ширшим є графік функції
,
тим ширшим є графік функції
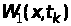 .
.
На
основі ансамблю з
 реалізацій випадкового процесу
статистичне визначення дисперсії
проводимо за формулою:
реалізацій випадкового процесу
статистичне визначення дисперсії
проводимо за формулою:
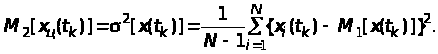 (24)
(24)
Визначимо перший та другий центральні моменти для рівномірного та експоненційного законів (табл.1 та 2).
Рівномірний закон. Оскільки математичне сподівання для цього випадку дорівнює нулеві, то обидва центральні моменти збігаються з початковими моментами, тобто
 ,
,
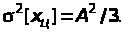
Експоненційний закон. Перший центральний момент за означенням дорівнює нулеві. Другий центральний момент (дисперсія), згідно з (22), визначаємо за формулою:
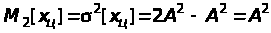 .
.
При розв'язуванні багатьох практичних завдань доводиться додавати, віднімати та перемножувати випадкові сигнали. При цьому числові характеристики результуючих сигналів достатньо просто визначають через числові характеристики первинних сигналів.
Наприклад,
якщо
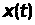 та
та
 є первинними незалежними сигналам,
є первинними незалежними сигналам,
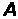 –
постійна величина, то справедливі такі
співвідношення:
–
постійна величина, то справедливі такі
співвідношення:
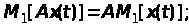 (25)
(25)
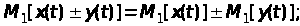 (26)
(26)
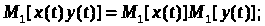 (27)
(27)
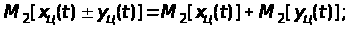 (28)
(28)
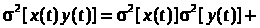
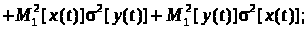 (29а)
(29а)
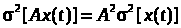 .
(29б)
.
(29б)
Подані
співвідношення можна узагальнити на
випадок більшої кількості випадкових
сигналів. У загальному випадку числові
характеристики одновимірних розподілів
залежать від часу. Це зумовлюється
часовою залежністю функції розподілу
 та одновимірної густини розподілу
та одновимірної густини розподілу
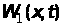 .
Тому в цьому разі числові характеристики
замість чисел стають функціями часу і
їх називають моментними функціями. На
рис. 5a зображена реалізація випадкового
процесу, перша моментна функція якого
(середні значення) не змінюється в часі
і дорівнює нулеві, а центральна моментна
функція другого порядку (дисперсія) з
часом зростає. Рисунок 5б ілюструє
варіант реалізації випадкового процесу
з незмінною дисперсією та змінним у
часі середнім значенням.
.
Тому в цьому разі числові характеристики
замість чисел стають функціями часу і
їх називають моментними функціями. На
рис. 5a зображена реалізація випадкового
процесу, перша моментна функція якого
(середні значення) не змінюється в часі
і дорівнює нулеві, а центральна моментна
функція другого порядку (дисперсія) з
часом зростає. Рисунок 5б ілюструє
варіант реалізації випадкового процесу
з незмінною дисперсією та змінним у
часі середнім значенням.
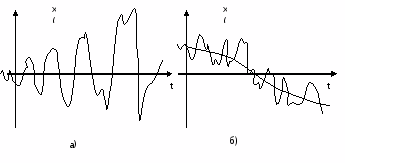
Рисунок 5 – Варіанти реалізацій випадкового процесу із змінними в часі числовими характеристиками.
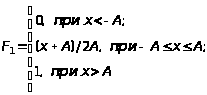
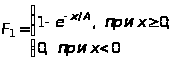
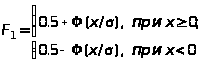
 -
інтеграл імовірностей
-
інтеграл імовірностей