Разработка математической модели электронного устройства
Курсовая работа
по курсу
“Моделирование в электронике”
”Разработка математической модели электронного устройства"
Содержание
Введение
1. Анализ поставленной задачи
2. Расчет переходного процесса на основе численных методов решения дифференциальных уравнений
2.1 Разработка математической модели и её решение с использованием метода пространства состояний
2.2 Составление математической модели с помощью матрично-векторного метода
3. Разработка алгоритма и программ модели
4. Исследование схемы в частотной области
Заключение
Литература
Приложения
Введение
Развитие вычислительной техники и повышение требований к разрабатываемой электронной аппаратуре выдвинули на первый план создание систем автоматизированного проектирования. До начала шестидесятых годов вычислительные методы использовались при анализе и проектировании цепей крайне незначительно. Квалифицированный инженер мог синтезировать простые цепи, пользуясь минимумом вычислений. Он создавал макет схемы, производил измерения и различные модификации и в результате получал конечный вариант цепи. За последние годы ситуация значительно изменилась. Появились интегральные схемы и стали доступными ЭВМ. Оба эти обстоятельства повлияли друг на друга. Интегральные схемы сделали возможным производство более совершенных и дешевых ЭВМ, а те, в свою очередь, облегчили проектирование новых интегральных схем. Относительно дешевые ЭВМ стали широкодоступными, так что малые фирмы и даже индивидуальные пользователи могут себе позволить их иметь. Несомненно, что в этой связи вычислительные методы будут иметь все большее значение. Рассмотрев эту проблему под другим углом зрения, можно заключить, что технологический прогресс сделал возможным проектирование больших функциональных блоков, содержащей в одной схеме тысячи взаимосвязанных транзисторов. Очевидно, разработка такой схемы невозможна при экспериментальной отладке на макете. Изучением методов разработки моделей, электронных компонентов, их устройств, а также решением этих моделей и определением их параметров занимается моделирование. Моделирование это исследование каких-либо явлений, процессов или систем путём построения и изучения их моделей, использование моделей для определения или уточнения характеристик и рационализации способов построения вновь конструированных объектов.
Модель (фр. modele, лат. modulus) образ (аналог, изображение, описание, схема, чертеж, график, план, карта и т.п.) какого-либо процесса, объекта или явления, используемый в качестве его заместителя. Для анализа физических систем с использованием цифровых, аналоговых или гибридных ЭВМ применяется метод математического моделирования. Это описание поведения физической системы при помощи математических уравнений или соотношений называется математическими моделями. Воспроизведение математической модели на ЭВМ называется машинным моделированием. При этом машина становится рабочей моделью физической системы. Определение переменных математической модели, взаимосвязанных с переменными изучаемого физического процесса и отражающихся основным законом его поведения при заданных начальных условиях и внешних воздействиях, даёт решение задачи моделирования. При решении задачи моделирования выполняются следующие этапы:
постановка задачи;
получение математической модели;
выбор и применение метода решения;
разработка алгоритма решения;
написание программы на ЭВМ;
отладка программы, корректировка ошибок;
реализация программы на ЭВМ, расчет и оценка результатов.
Результат реальных измерений исследуемого явления или объекта и результаты расчета на ЭВМ обрабатываются, сравниваются и рассчитываются поправки к математической модели. Учёт поправок приводит к более точной математической модели. Этот замкнутый процесс повторяется до тех пор, пока не достигается требуемая точность совпадения реальных и имитационных данных. Важным характером математической модели является степень её адекватности реальному процессу и её реализуемость на имеющихся технических средствах.
1. Анализ поставленной задачи
Согласно варианта задания №25 в рамках курсовой работы необходимо произвести следующие расчеты для схемы рис.1.1:
Р
исунок
1.1 Структурная
схема устройства
1) Определить длительность и
вид переходного процесса при подаче на
вход схемы единичного скачка напряжения
(найти
)
рис.1.2
Рисунок 1.2 График зависимости U>вх> от t
2) Рассчитать частотные характеристики цепи. Определить АЧХ и ФЧХ.
3) Проанализировать зависимость вида переходного процесса от параметров схемы.
2. Расчет переходного процесса на основе численных методов решения дифференциальных уравнений
2.1 Разработка математической модели и её решение с использованием метода пространства состояний
При рассмотрении физической системы как объекта исследования или проектирования целесообразно распределить все переменные, характеризующие систему, или имеющие к ней какое-либо отношение на три множества:
1) Входные переменные, характеризующие внешнее воздействие на входы системы.
2) Переменные состояния внутренние (промежуточные) переменные, совокупность которых полностью характеризует свойства системы.
3) Выходные переменные, представляющие реакцию системы на внешние воздействия и те состояния системы, которые представляют интерес для исследователя.
Собственно система, её входы и выходы это три взаимосвязанных объекта, которые в каждом конкретном случае однозначно описывают систему. В зависимости от того, какой из объектов подлежит определению при остальных двух заданных различают три типа задач исследования проектирования: анализ, синтез и измерения. Решение любой из этих задач связано с исследованием состояний системы, множество которых образует пространство состояний.
Переменными состояниями динамической системы является минимальный набор переменных или чисел, содержащих информацию о предыстории системы, достаточную для полного определения её поведения в настоящий и будущий момент времени при известных возмущениях, воздействующих в настоящий момент. Они выбираются так, чтобы имели физический смысл.
Выбор переменных состояний не является однозначным, т.е. разные наборы переменных состояний дают разные описания одного объекта. Уравнения, описывающие поведение системы и определяющие всю вышеуказанную информацию, называются уравнениями состояния.
Для схемы устройства, приведенной на рис.2.1, получим выражение для передаточной функции, которая представляет собой отношение выходного сигнала ко входному, преобразованные по Лапласу при начальных нулевых условиях. Для этого составим систему уравнений, используя метод контурных токов.
Рисунок 2.1 Структурная схема устройства
Составляем уравнения для каждого
Выражаем из системы
Перейдём от передаточной функции W (p) к дифференциальному уравнению.
Представим дифференциальное уравнение во временной области:
или
где: А>2>=4R2C2A>1>=6RCA>0>=1
Полученное дифференциальное уравнение является математической моделью и описывает поведение анализируемого устройства. Решим эту математическую модель с использованием метода пространства состояний.
Уравнение является дифференциальным уравнением второго порядка. Приведём его к системе уравнений первого порядка и решим эту систему.
Выражаем дифференциальное уравнение относительно старшей производной:
Осуществляем цепочку замен:
Пусть
,
тогда
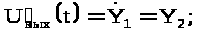
По полученной системе уравнений сформируем структурную схему нашей математической модели, где операцию интегрирования обозначим с помощью интегратора.
Р
исунок
2.2 Структурная
схема алгоритма решения нашего
дифференциального уравнения
Запишем матрицу коэффициентов переменных состояний:
На следующем этапе анализа системы составляем строки для подпрограммы, реализующей метод Рунге-Кутта, осуществляем запуск программы и получаем результат в виде числового и графического материала.
Для анализа системы зададимся в исходном случае следующими значениями сопротивления и ёмкости: R = 100 Ом; С = 0,1 Ф.
Тогда коэффициенты в матрице будут иметь следующие значения:
A>0 >= 1; A>1 >= 60 (ОмФ); A>2 >= 400 (ОмФ) 2
Составляем строки для подпрограммы:
500 F (1) =H*y2
510 F (2) =H*Y (3)
520 F (3) =H* (-A0/A2Y ())
Осуществляем запуск программы RUNKUT. BAS (приложение 2), в режиме диалога вводим следующие значения:
МЕТОД РУНГЕ-КУТТА ДЛЯ N УРАВНЕНИЙ
НАЧ. И КОН. ЗНАЧЕНИЕ АРГУМЕНТА (X,XK)? 0,50
КОЛИЧЕСТВО ФУНКЦИЙ N? 2
ВВЕДИ КОЛИЧЕСТВО ТОЧЕК М? 1500
ЧЕРЕЗ СКОЛЬКО ТОЧЕК ВЫВОДИТЬ НА ЭКРАН?? 150
НАЧ. ЗНАЧЕНИЯ ФУНКЦИЙ
Y (1) =? 0
Y (2) =? 0
В результате получаем решение (приложение 3, а).
Определим длительность
переходного процесса, как
,
где r>min>
- минимальный корень соответствующего
характеристического уравнения, которое
мы получим, если приравняем левую часть
нашего неоднородного дифференциального
уравнения к нулю, если корни действительные
и вещественная часть корня, если корни
комплексные.
Соответственное характеристическое уравнение имеет вид:
Корни этого уравнения будем искать по формуле:
Где: A>0 >= 1; A>1 >= 60; A>2 >= 400
То есть:
То есть время переходного процесса:
Увеличиваем емкость С в 5 раз: R = 100 Ом; С = 0,5 Ф.
Тогда коэффициенты в матрице будут иметь следующие значения:
A>0 >= 1; A>1 >= 300 (ОмФ); A>2 >= 10000 (ОмФ) 2
Составляем строки для подпрограммы:
500 F (1) =H* (1/10000*Y (1) - 300/10000*Y (2) +1/10000)
510 F (2) =H*Y (2)
Осуществляем запуск программы RUNKUT. BAS (приложение 2), в режиме диалога вводим следующие значения:
МЕТОД РУНГЕ-КУТТА ДЛЯ N УРАВНЕНИЙ
НАЧ. И КОН. ЗНАЧЕНИЕ АРГУМЕНТА (X,XK)? 0, 200
КОЛИЧЕСТВО ФУНКЦИЙ N? 2
ВВЕДИ КОЛИЧЕСТВО ТОЧЕК М? 1500
ЧЕРЕЗ СКОЛЬКО ТОЧЕК ВЫВОДИТЬ НА ЭКРАН?? 150
НАЧ. ЗНАЧЕНИЯ ФУНКЦИЙ
Y (1) =? 0
Y (2) =? 0
В результате получаем решение (приложение 3, б).
Найдем время переходного процесса при этих параметрах.
Где
A>0> = 1; A>1> = 300; A>2> = 10000
Время переходного процесса:
2.2 Составление математической модели с помощью матрично-векторного метода
Для автоматизации анализа переходных процессов наибольшее распространение получили матричные методы контурных токов и узловых потенциалов.
Метод контурных токов
Н
а
рисунке 3.1 показана принципиальная
схема устройства.
Рисунок 3.1 Структурная схема устройства
Для анализируемой схемы составим матрицу сопротивлений по следующему правилу:
1) Диагональные элементы матрицы положительны и равны сумме сопротивлений, входящих в данный контур.
2) Внедиагональные элементы Z>ij> отрицательны, сопротивления внедиагональных элементов равны сопротивлениям общих элементов для контуров с номерами ij. Кроме того Z>ij>= Z>ji>.
3) Исходная матрица сопротивлений является симметричной относительно главной диагонали.
4) Элемент E>i> вектора напряжений с номером i равен сумме напряжений независимых источников, входящих в i-й контур.
Составляем матрицу сопротивлений для данной схемы:
Так как данная матрица даёт нам дифференциальные уравнения, содержащие интегралы, то нам необходимо избавиться от знаменателя, для этого воспользуемся компонентными уравнениями:
Пополним исходную систему по методу контурных токов вышеприведенными компонентными уравнениями. Запишем результирующую матрицу, дополненную компонентными уравнениями:
Разделяем матрицу на две части: содержащие множитель p составляющие оставляем в левой части, а составляющие без множителя p переносим в правую часть:
Запишем первые 3 строки матрицы в виде системы уравнений для выражения токов через напряжения без производных:
,
Откуда
Перепишем 3последние строки матрицы в виде системы уравнений:
Подставляя значения токов в уравнения предыдущей системы, получаем систему дифференциальных уравнений:
Нам необходимо исследовать
характер изменения величины выходного
напряжения U>вых>.
Анализируя схему (рис.3.1), можно записать:
Для анализа системы зададимся следующими значениями сопротивления и ёмкости: R = 100 Ом; С = 0,1 Ф.
Составляем строки для подпрограммы:
500 F (1) =H/0,2* (-Y (1) +Y (2))
510 F (2) =H/0,2* (1+Y (1) - 2*Y (2))
Осуществляем запуск программы RUNKUT. BAS (приложение 2), в режиме диалога вводим следующие значения:
МЕТОД РУНГЕ-КУТТА ДЛЯ N УРАВНЕНИЙ
НАЧ. И КОН. ЗНАЧЕНИЕ АРГУМЕНТА (X,XK)? 0,250
КОЛИЧЕСТВО ФУНКЦИЙ N? 2
ВВЕДИ КОЛИЧЕСТВО ТОЧЕК М? 1500
ЧЕРЕЗ СКОЛЬКО ТОЧЕК ВЫВОДИТЬ НА ЭКРАН?? 150
НАЧ. ЗНАЧЕНИЯ ФУНКЦИЙ
Y (1) =? 0
Y (2) =? 0
В результате получаем решение (приложение 4).
3. Разработка алгоритма и программ модели
Для численной реализации полученных результатов необходимо решить систему дифференциальных уравнений первого порядка. В ручную это делать очень неудобно и долго, для этого целесообразно написать программу, которая выдавала бы решение в численном и графическом виде. Современная компьютерная база позволяет сделать это.
Прежде всего, определимся с методом решения. Выберем один из методов Рунге - Кутта. Разные представители этой категории методов требуют большего или меньшего объема вычислений соответственно обеспечивают большую или меньшую точность. Эти методы имеют рад важных преимуществ:
Являются явными, одноступенчатыми,
т.е. значение
вычисляется
по ранее найденным значениям
.
Допускают использование изменяемого шага, что дает возможность уменьшать его там, где функция быстро изменяется, и увеличивать в противоположном случае.
Легки в использовании, потому
что для начала расчета достаточно
выбрать сетку
и
задать значение
.
Согласуются с рядом Тейлора
включительно до членов порядка
,
где степень p неодинакова
для разных методов и называется порядком
метода.
Не требуют вычисления
производных от
,
а требуют лишь вычисления самой функции.
Если
непрерывна и ограничена вместе со своими
четвертыми производными, то хорошие
результаты дает метод четвертого
порядка. Он описывается системой
следующих соотношений:
(
);
Алгоритм метода Рунге - Кутта:
Выбираем начальный шаг h на отрезке [a,b], задаем точность ε.
Создаем множество равноудаленных точек (узлов)
Находим решение y>i+1>> >по формулам при шаге h и при шаге h/2, 0 ≤ i ≤ n-1.
Проверяем неравенство
.
Если это неравенство
выполняется, то принимаем
и продолжаем вычисление
с
тем же шагом, если нет, то уменьшаем
начальный шаг h в 2
раза и переходим к пункту 3.
Если ограничиться одним шагом, то у нас точность не будет задаваться.
Алгоритм программы реализации этого метода выражен блок - схемой и представлен в приложении 1.
Написание и отладка программы.
Программа написана в среде gwBasic и представляет собой откомпилированный файл runkut. bas. Реализован автоматический подбор масштаба вывода графика на дисплей. Данная программа была написана и полностью отлажена, так что представляет собой полностью готовое к работе приложение.
Инструкция пользователя.
При работе с данной программой необходимо произвести следующие действия:
Запустить среду gwBasic
Нажать F3, ввести runkut. bas, программа загрузится в память.
Ввести LIST 500 - 530, отобразятся эти строки
В данных строках ввести коэффициенты при Y>1>, Y>1>, и так далее. Значение производной представляется в виде F (1), F (2) и т.д.
Вводите run. Программа запросит интервал расчета, кол-во функций, кол-во точек, интервал между выводимыми точками и начальные значения функций.
После ввода всей информации пункта 5 будут выводиться численные данные, а в конце - графики.
4. Исследование схемы в частотной области
Исследование схемы в частотной области проводится при подаче на вход схемы синусоидального напряжения. Исследование проводится для определения таких характеристик, как: коэффициент колебательности, полоса пропускания, частота среза и резонансная частота.
Передаточная характеристика является комплексной функцией, ее модуль - это амплитудно-частотная характеристика (АЧХ), а аргумент - фазо-частотная (ФЧХ).
АЧХ - амплитудно-частотная характеристика тракта. Это - частотная зависимость отношения нормированных амплитуд синусоидальных сигналов на выходе и входе тракта. АЧХ лишь косвенно характеризует свойства тракта при передаче несинусоидальных сигналов.
ФЧХ - фазо-частотная характеристика. Это - частотная зависимость разности фаз синусоидальных сигналов на выходе и входе тракта.
Перепишем передаточную функцию, полученную в пункте 2:
В уравнении передаточной функции p заменим на j [7] и произведем преобразования таким образом, чтобы разделить вещественную и мнимую часть:
Где P () - вещественная частотная характеристика;
Q () - мнимая частотная характеристика.
Здесь
Тогда
Функция K () называется амплитудно-частотной характеристикой (АЧХ), а
-
фазо-частотной характеристикой (ФЧХ).
В приложении 5 приведены графики АЧХ и ФЧХ для R =10 (Oм) и С = 0.1 (Ф).
Проанализируем графики:
Показатель колебательности:
.
Полоса пропускания (интервал
частот, где выполняется условие
):
0. .0.185 (рад/с)
Частота среза (частота, в
которой
):
ω>ср> = 0 (рад/с).
Резонансная частота (в ней
имеет максимум): 0 (рад/с)
Заключение
В заключение можно сделать следующие выводы:
Разработана математическая модель, которая была решена с помощью метода пространства состояний.
Также разработана модель переходного процесса на основе матричных методов контурных токов и узловых потенциалов. Была проведена сравнительная характеристика этих двух методов для решения заданной модели.
Разработан алгоритм к программе решения модели. С помощью ЭВМ численно и графически проанализирована исходная модель.
Анализируя полученные результаты, можно сказать, что наша система устойчива и монотонна, о чем свидетельствуют графики в приложении 3 (а и б). Так же очевидно что мы можем влиять на длительность переходного процесса меняя номиналы R и C. Это тоже подтверждается графиками: увеличение емкости с С=0.1 (Ф) до С=0.5 (Ф) привело к увеличению длительности переходного процесса с τ=22,92 (с) до τ =114,59 (с).
Исследование схемы в частотной области также дает нам возможность оценить устойчивость схемы. Наш показатель колебательности М = 1 свидетельствует о том, что мы имеем дело с устойчивой системой.
Литература
Ажогин В.В., Згуровский М.З. Моделирование на цифровых, аналоговых и гибридных ЭВМ. М: Радио и связь, 1983.
Влах И., Сингхал К. Машинные методы анализа и проектирования электронных схем. М: Радио и связь, 1988.
Гринчишин Я.Г., Ефимов В.И., Ломякович А.Н. Алгоритмы и программы на языке Basic. М: Радио и связь, 1988.
Дьяконов В.П. Справочник по алгоритмам и программам на языке Basic для персонального ЭВМ. М: Радио и связь 1987.
Нерретер В. Расчёт электрических цепей на персональной ЭВМ. М: Радио и связь, 1991.
Сигорский В.П. Математический аппарат инженера. М: Радио и связь, 1975.
Бессонов Л.А. Теоретические основы электротехники. - М: Высшая школа. 1964.
Приложения
Приложение 1
Б
локсхема
алгоритма
Начало
Приложение 2
Листинг программы RUNKUT. BAS
10 PRINT "МЕТОД РУНГЕ-КУТТА ДЛЯ N УРАВНЕНИЙ "
20 INPUT "НАЧ. И КОН. ЗНАЧЕНИЕ АРГУМЕНТА (X,XK)"; X,XK
30 INPUT "КОЛИЧЕСТВО ФУНКЦИЙ N"; N
31 INPUT "ВВЕДИ КОЛИЧЕСТВО ТОЧЕК М"; M
32 INPUT "ЧЕРЕЗ СКОЛЬКО ТОЧЕК ВЫВОДИТЬ НА ЭКРАН?"; Z1
40 DIM Y (6),Y1 (6),K1 (6),F (6),X (1500),FY (6,1500)
50 PRINT "НАЧ. ЗНАЧЕНИЯ ФУНКЦИЙ"
60 FOR I=1 TO N
61 PRINT "Y ("I;
62 INPUT ") ="; Y (I)
63 NEXT I
100 H= (XK-X) /M: MC= (XK-X) /20: Z9=0
101 FOR I=1 TO N
102 Y1 (I) =Y (I): Y9 (I) =0
103 NEXT I
110 FOR I=1 TO M
120 GOsub> 500
130 FOR L=1 TO N
131 K1 (L) =F (L)
132 Y (L) =Y1 (L) +F (L) /2
133 NEXT L
140 X=X+H/2
141 GOsub> 500
150 FOR L=1 TO N
151 K1 (L) =K1 (L) +2*F (L)
152 Y (L) =Y1 (L) +F (L) /2
153 NEXT L
160 GOsub> 500
170 FOR L=1 TO N
171 K1 (L) =K1 (L) +2*F (L)
172 Y (L) =Y1 (L) +F (L)
173 NEXT L
180 X=X+H/2
181 GOsub> 500
182 FOR L=1 TO N
183 Y (L) =Y1 (L) + (K1 (L) +F (L)) /6
184 Y1 (L) =Y (L)
185 NEXT L
186 X (I) =X
190 IF I MOD Z1=0 THEN PRINT X,
191 FOR L=1 TO N: FY (L, I) =Y (L)
192 IF I MOD Z1=0 THEN PRINT FY (L, I),
193 IF FY (L, I) >=Y9 (L) THEN Y9 (L) =FY (L, I)
194 NEXT L
195 IF I MOD Z1=0 THEN PRINT: Z=Z+1
200 IF Z=11 THEN 226 ELSE GOTO 228
226 Z=1: PRINT "ЖМИ ЛЮБУЮ КЛАВИШУ: *******"
227 IF LEN (INKEY$) =0 THEN 227 ELSE GOTO 228
228 NEXT I
229 PRINT "КОНЕЦ РАСЧЕТА ПЕРЕХОДНОГО ПРОЦЕССА: ЖМИ ЛЮБУЮ КЛАВИШУ."
230 IF LEN (INKEY$) =0 THEN 230 ELSE GOTO 231
231 FOR I=1 TO N
232 M (I) =Y9 (I) /7: PRINT "МАСШТАБ ДЛЯ Y ("; I; ")"; M (I); "ЕДЕНИЦ В 1 СМ"
233 IF I=1 THEN M (I) =30.5/M (I) ELSE M (I) =13.34/M (I)
234 NEXT I
235 PRINT "ДЛЯ ПРОДОЛЖЕНИЯ ЖМИ ЛЮБУЮ КЛАВИШУ."
240 PRINT " ФАЗОВЫЙ ПОРТРЕТ СИСТЕМЫ"
241 IF LEN (INKEY$) =0 THEN 241 ELSE GOTO 262
262 GOTO 1010
500 F (1) =H* (-1.8/.216*Y (1) +Y (2))
510 F (2) =H* (-3.6/.216*Y (1) +Y (3))
520 F (3) =H* (-.6/.216*Y (1) +1/.216)
530 RETURN
1010 SCREEN 2: KEY OFF: CLS
1030 LINE (0,0) - (639, 199),7,B
1040 LINE (0,100) - (639,100),7
1050 LINE (320,0) - (320, 199),7
1060 FOR I=1 TO M
1061 A=FY (1, I) *M (1)
1062 A%=CINT (A) +320
1070 FOR L=2 TO N
1073 B=FY (L, I) *M (L)
1074 B%=100-CINT (B)
1080 PSET (A%,B%),7
1090 NEXT L
1100 NEXT I
1110 Z$=INKEY$: IF LEN (Z$) =0 GOTO 1110
1120 SCREEN 0: CLS
2000 PRINT " РАЗВЕРТКА ПО ВРЕМЕНИ"
2010 PRINT "МАСШТАБ ПО ВРЕМЕНИ: "; MC; " СЕК В 1 СМ ЭКРАНА."
2020 PRINT "ЖМИ ЛЮБУЮ КЛАВИШУ ДЛЯ ПРОДОЛЖЕНИЯ ***********"
2030 IF LEN (INKEY$) =0 THEN 2030 ELSE 2040
2040 MC=30.5/MC
2050 SCREEN 2: CLS: KEY OFF
2080 LINE (0,0) - (639, 199),7,B
2090 LINE (0,100) - (639,100),7
2091 M (1) =Y9 (1) /7: M (1) =13.34/M (1)
2110 FOR I=1 TO M
2120 A=X (I) *MC
2130 A%=CINT (A)
2140 FOR L=1 TO N
2150 B=FY (L, I) *M (L)
2160 B%=100-CINT (B)
2170 PSET (A%,B%),7
2180 NEXT L
2190 NEXT I
2200 Z$=INKEY$: IF LEN (Z$) =0 GOTO 2200
2210 SCREEN 0: CLS
2230 END
Приложение 3
Результаты решения модели с помощью метода пространства состояний
а) Исходный случай:
R=100 Ом; С=0,1Ф;
A>0>=1; A>1>=60 (ОмФ); A>2>=400 (ОмФ) 2;
Результат решения в виде числового материала:
TY (1) Y (2)
20.000040.21335444.563361E-02
40.000080.45550427.862294E-02
59.999770.62781770.1012733
79.999470.74593830.1167423
99.99160.82659530.127301
119.99890.8816480.1345075
139.99860.91922260.1394261
159.99830.94486770.1427831
17.99790.96237140.1450744
199.99760.97431790.1466382
МАСШТАБ ДЛЯ Y (1) 0.1391883 ЕДИНИЦ В 1 СМ
МАСШТАБ ДЛЯ Y (2) 2.094832E-02 ЕДИНИЦ В 1 СМ
РАЗВЕРТКА ПО ВРЕМЕНИ
МАСШТАБ ПО ВРЕМЕНИ: 85 СЕК В 1 СМ ЭКРАНА.
Y1
Y2
б) R=100 Ом; С=0,5Ф;
A>0> = 1 (ОмФ); A>1> = 300 (ОмФ); A>2> = 10000 (ОмФ)2;
Результат решения в виде числового материала:
T Y(1) Y(2)
169.9998 0.3903698 1.399509E-02
340.0018 0.6805174 2.163532E-02
510.006 0.833094 2.563034E-02
680.0013 0.91281 2.771734E-02
849.9963 0.9544531 2.880757E-02
1019.991 0.9762068 2.937709E-02
1189.987 0.9875708 0.0296746
1359.982 0.9935071 2.983002E-02
1529.977 0.9966082 0.0299112
1699.972 0.9982281 2.995361E-02
МАСШТАБ ДЛЯ Y( 1 ) 0.142604 ЕДИНИЦ В 1 СМ
МАСШТАБ ДЛЯ Y( 2 ) 4.279087E-03 ЕДИНИЦ В 1 СМ
РАЗВЕРТКА ПО ВРЕМЕНИ
МАСШТАБ ПО ВРЕМЕНИ: 10 СЕК В 1 СМ ЭКРАНА.
Y1
Y2
Приложение 4
Результаты решения модели с помощью методов контурных токов
Результат решения в виде числового материала:
T Y(1) Y(2)
25.00005 0.2801473 0.5406263
49.99982 0.5496613 0.7211265
74.99994 0.7204853 0.8272296
100.0007 0.826595 0.9828291
125.0015 0.8924267 0.933516
150.0002 0.9332659 0.9587562
174.9987 0.9586008 0.9744139
199.9972 0.9743177 0.9841274
224.9956 0.9840681 0.9901535
249.9941 0.9901165 0.9938917
МАСШТАБ ДЛЯ Y( 1 ) 0.1414452 ЕДИНИЦ В 1 СМ
МАСШТАБ ДЛЯ Y( 2 ) 0.1419845 ЕДИНИЦ В 1 СМ
РАЗВЕРТКА ПО ВРЕМЕНИ
МАСШТАБ ПО ВРЕМЕНИ: 12.5 СЕК В 1 СМ ЭКРАНА.
Y2
Y1=Uвых
Приложение 5
АЧХ
ФЧХ
