Приемная антенна для СТВ

Министерство образования Российской Федерации.

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ

(ТУСУР).

Кафедра сверхвысоких частот и квантовой радиотехники
(СВЧиКР).

Курсовая работа по дисциплине Антенны и устройства СВЧ.

Приемная антенна для СТВ

Студент гр.:

_____

“__”______.

Преподаватель:

_____.

“__”______.

Реферат

Пояснительная записка содержит стр. 16., рисунков 11, таблицы 2.

АНТЕННА, РУПОР, ПОЛЯРИЗАТОР, СТВ, ДИАГРАММА НАПРАВЛЕННОСТИ, ОБЛУЧАТЕЛЬ, ЗЕРКАЛО

В курсовом проекте была рассчитана зеркальная антенна для приема СТВ.

Курсовой проект выполнен с использованием текстового редактора Microsoft World 2000 для Windows 2000 и MathCAD 11а Enterprise.

Введение 4

2. Расчет параболической антенны. 5

2.1. Расчет облучателя. 5

2.1.1. Определение угла раскрыва параболоида 6

2.2 Расчет параболоида. 7

2.2.1 Определение диаметра параболоида 2R_>п> и фокусного расстояния f 7

2.3 Расчет диаграммы направленности. 8

2.4 Расчёт G антенны 10

3. Расчет принятой мощности. 11

3.1 Затухания в свободном пространстве. 11

3.1.1 Затухания в тропосфере. 11

3.2.2 Затухания в ионосфере. 13

4. Принцип действия ферритового поляризатора. 15

Список использованных источников. 16

Введение

Широкое распространение в диапазоне СВЧ получили остронаправленные широкодиапазонные антенные устройства, аналогичные оптическим рефлекторам или прожекторам. С помощью них оказалось возможным радиорелейная связь, межконтинентальные телевизионные передачи (спутниковая связь), связь с космическими объектами, радиоастрономия, радиолокация и некоторые другие практические приложения радиотехники СВЧ.

Зеркальные антенны характерны тем, что их геометрические размеры намного превосходят длину волны. Они подобны оптическим приборам и электромагнитные процессы в таких антеннах приближенно могут быть описаны с помощь законов геометрической оптики. Поэтому внешний вид некоторых антенн напоминают оптические линзы и зеркала, которые в радиотехнике преобразуют сферические и цилиндрические волны в плоские.

Зеркальные антенны составлены из облучателя и зеркальной поверхности. В качестве облучателя используется любая слабонаправленная антенна, в данном случае открытый конец прямоугольного волновода.

2. Расчет параболической антенны.

2.1. Расчет облучателя.

Так как облучатель является важнейшим элементов зеркальной антенны, в значительной степени определяющим ее параметры, то расчет обычно начинается с выбора облучателя. Основными критериями для его выбора являются рабочая длина волны, требования к диапазонности, тип фидера, величина подводимой мощности, близкий к сферическому фронт волны в пределах угла раскрыва зеркала (с допуском порядка ±λ/16), диаграмма направленности с концентрацией энергии в пределах одной полусферы, хорошее согласование с фидером, малое затенение и ряд специфических требований, обусловленных особенностями радиотехнического устройства, где используется антенна.

Облучатели в виде открытого конца волновода или рупора удобно использовать при больших мощностях излучения. Они обладают также хорошими диапазонными свойствами. Однако открытый конец прямоугольного волновода обладает разными диаграммами направленности в плоскостях E и Н. От этого недостатка свободны рупорные облучатели, где имеется возможность почти независимой регулировки диаграмм направленности в плоскостях Е и Н путем подбора размеров раскрыва рупора и , таким образом получения диаграммы в виде тела вращения.

Т

(2.1.1)

ак как для большинства облучателей антенна получается оптимальной, когда уровень облучения края зеркала на 10 дБ ниже уровня его центра (0,316 по напряженности поля), то диаграмма направленности облучателя должна удовлетворять соотношению

где – угол раскрыва параболоида.

Как известно, нормированное распределение поля на раскрыве зеркала связано с диаграммой направленности облучателя м параметрами парабалоида соотношением

(2.1.2)

где f – фокусное расстояние, – расстояние от фокуса до точки на поверхности зеркала.

Диаграмму направленности небольшого рупора можно рассчитать при помощи следующих приближенных соотношений

((2.1.3)

где – нормированные диаграммы направленности по напряженности поля в плоскостях Е и Н соответственно;

– угол, отсчитываемый от направления максимума диаграммы направленности;

– размер раскрыва рупора в плоскости Н;

– размер раскрыва рупора в плоскости E;

, где

2.1.1. Определение угла раскрыва параболоида

После выбора излучателя следует найти соотношение между радиусом параболоида

определим из следующего соотношения и фокусным расстоянием (рис. 2.1) при помощи выражения

(2.1.4)

Рис. 2.1

Чтобы определить угол раскрыва выбирается в пределах , выберем его равным 0.5, тогда

С помощью выражений (2.1.2),(2.1.3) получим следующие уравнения

(2.1.5)

Решим уравнения (2.1.5) с помощью графиков функций (рис. 2.2)

Рис. 2.2 Графики функций

откуда

2.2 Расчет параболоида.

2.2.1 Определение диаметра параболоида 2R_>п> и фокусного расстояния f

Из приближенной формулы для КНД найдем радиус параболоида R_>п>

(2.2.1)

где - площадь раскрывa парабалоида.

(2.2.2)

Следовательно,

Фокусное расстояние можно определить пользуясь формулой

(2.2.3)

Диаметр парабалоида связан с заданной длиной волны и требуемым углом раствора диаграммы направленности на уровне половинной мощности (2_>0.5>) приближенной зависимостью

(2.2.4)

Тогда

2.3 Расчет диаграммы направленности.

Используя формулы (2.1.3) построим нормированную диаграмму направленности облучателя.

Рис. 2.3.1. Диаграмма направленности облучателя в полярной системе координат

Найдем распределение поля в раскрыве параболоида, для этого воспользуемся следующей формулой

(2.3.1)

где .

Полученные данные занесем в таблицу 2.3.1.

Таблица 2.3.1

	sin()	cos()						F(R)	F1(R)	F2(R)
0 5,3 10,6 15,9 21,2 26,5 31,8 37,1 42,4 47,7	0 0.092 0.184 0.274 0.362 0.446 0.527 0.603 0.674 0.74 0.799	1 0.996 0.983 0.962 0.932 0.895 0.85 0.798 0.738 0.673 0.602	0.54 0.541 0.545 0.551 0.559 0.57 0.584 0.601 0.621 0.646 0.674	1 0.998 0.991 0.981 0.966 0.947 0.925 0.899 0.869 0.837 0.801	1 0.99 0.961 0.914 0.853 0.782 0.705 0.625 0.547 0.473 0.405	0 0.05 0.1 0.151 0.202 0.254 0.308 0.362 0.419 0.477 0.538	0 0.093 0.186 0.279 0.374 0.471 0.57 0.671 0.776 0.884 0.997	1 0.988 0.953 0.897 0.825 0.741 0.652 0.562 0.475 0.396 0.325	1 0.994 0.977 0.947 0.905 0.85 0.781 0.696 0.594 0.472 0.329	1 0.988 0.954 0.899 0.824 0.734 0.633 0.529 0.432 0.357 0.325

Рис. 2.3.2 Распределение поля на раскрыве рупора

По найденному распределению поля на раскрыве вычисляется диаграмма направленности зеркальной антенны . Картина распределения поля на раскрыве зеркала может быть аппроксимирована при помощи соотношения:

(2.3.2)

где - равномерная часть распределения поля;

- неравномерная часть распределения поля;

n=1,2,3

Полученные значения (при n=1 и n=2) внесены в таблицу 2.3.1.

Как видно из таблицы 2.3.1, более точная аппроксимация распределения поля на раскрыве зеркала при n=2.

Выражение для нормированной диаграммы направленности антенны будет иметь вид:

(2.3.3)

где

n – показатель степени выражения, аппроксимирующего поле на раскрыве. (n=2)

Результаты расчета диаграммы направленности представим в виде таблицы 2.3.2

Таблица 2.3.2

, град	sin()		1(u)	31(u)	3(u)	3(u)
0 0.17 0.34 0.51 0.68 0.85 1.02 1.19 1.36 1.53 1.7	0 0.003 0.006 0.009 0.012 0.015 0.018 0.021 0.024 0.027 0.03	0 0.419 0.839 1.258 1.678 2.097 2.517 2.936 3.355 3.775 4.194	1 0.978 0.915 0.815 0.687 0.542 0.392 0.247 0.118 0.012 0.065	0.975 0.954 0.892 0.794 0.67 0.529 0.382 0.241 0.115 0.012 -0.064	1 0.985 0.93 0.9 0.837 0.81 0.74 0.627 0.498 0.392 0.316	0.675 0.665 0.628 0.608 0.565 0.547 0.5 0.423 0.336 0.265 0.213	1 0.981 0.921 0.85 0.748 0.652 0.535 0.402 0.273 0.168 0.09

Построим диаграмму направленности в декартовой системе координат

Рисунок 2.3.3 Диаграмма направленности антенны в декартовой системе координат

2.4 Расчёт G антенны

Расчёт G антенны будем вести по следующей формул

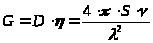(2.4.1)

где – коэффициент использования площади раскрыва зеркала, полностью определяется характером распределения поля в раскрыве.

S – геометрическая площадь раскрыва;

- коэффициент полезного действия параболической антенны (примем )

Коэффициент направленного действия (усиления), определенный по формуле (2.4.1) не учитывает потерь энергии на рассеивание, т.е. потерь энергии, проходящей от облучателя мимо зеркала.

3. Расчет принятой мощности.

3.1 Затухания в свободном пространстве.

Распространение УКВ на линии Земля-Космос осуществляется через тропосферу и ионосферу Земли и сопровождается ослаблением радиоволн. Ослабление обусловлено тремя причинами: поглощением радиоволн водяными парами и газами, поглощением и рассеянием различными гидрометеообразованиями (дождь, снег, облака, туман и т.п.) и поглощением радиоволн в ионосфере.

Сначала рассчитаем принятую мощность без учета влияния атмосферы, а затем найдем затухания в атмосфере.

Определим принятую мощность по формуле

(3.1.1)

где – коэффициент усиления приемной антенны.

– коэффициент усиления спутниковой антенны.

– расстояние до спутника.

Множитель ослабления в общем виде может быть записан следующим образом:

где - полный показатель ослабления на участке трассы проходящем в ионосфере;

- полный показатель ослабления на участке радиолинии в “чистой” атмосфере;

- полный показатель ослабления на участке радиолинии с гидрометеообразованиями;

3.1.1 Затухания в тропосфере.

Ослабление в “чистой” атмосфере и атмосферных образованиях происходит в результате поглощения энергии радиоволн и их рассеяния молекулами газов или взвешенными частицами вещества.

Полные показатели ослабления можно записать в виде:

(3.1.2.)

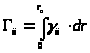(3.1.3.)

где и - коэффициенты ослабления в “чистой” атмосфере и в атмосферных образованиях

Показатель ослабления радиоволн в тропосфере зависит от угла места , т.е. от угла, под которым траектория волны направлена к горизонту (рис. 3.1.1). Так как плотность газов уменьшается с высотой, то наименьшая величина будет при распространении радиоволн в направлении, перпендикулярном к поверхности Земли ()

Рис. 3.1.1

Гидрометеообразования, или гидрометеоры (осадки, туман, облака и т.п.), вызывают ослабление электромагнитных волн, имеющих длину волны 3-5см и короче.

Коэффициент ослабления в тумане и облаках для водности, равной 1 представлен на рис. 3.1.2. Под водностью понимается количество водяного пара (в граммах), находящегося в одном кубическом метре воздуха. Водность тумана (облака) колеблется от 0,03 (слабый туман) до 2,3 (сильный туман).

Результаты расчетов для радиоволн сантиметрового и миллиметрового диапазонов, распространяющихся в дождях интенсивностью от 0.1мм/ч (очень слабый моросящий дождь) до 100 мм/ч (ливень), представлены в виде кривых (рис. 3.1.3). С увеличением интенсивности дождя и уменьшением длины волны коэффициент ослабления возрастает.

Рис. 3.1.3

Пользуясь графиками 3.1.1, 3.1.2, 3.1.3, определим суммарные показатели ослабления радиоволны в тропосфере , , для нашего случая ( или , , ).

при отсутствии дождя

при очень сильном дожде

3.2.2 Затухания в ионосфере.

Поглощение радиоволн в ионосфере обусловлено столкновениями электронов с нейтральными молекулами и ионами. В результате энергия радиоволны уменьшается вследствие частичного ее перехода в тепловую энергию.

(3.2.1)

где - коэффициент поглощения в ионосфере

(3.2.2)

где - относительная диэлектрическая проницаемость ионизированного газа;

- проводимость ионизированного газа.

(3.2.3)

(3.2.4)

где - электронная концентрация ионизированного газа (определяется из графика 3.2.1);

- число столкновений электронов с молекулами или с ионами в единицу времени (определяется из графика 3.2.2)

Рис 3.2.1 Рис. 3.2.2

Пользуясь графиками 3.2.1, 3.2.2, а также формулами 3.2.1-3.2.4 найдем коэффициент ослабления в ионосфере.

На данной частоте (12,5 ГГц) ослабление радиоволн в ионосфере отсутствует (очень мало по сравнению с ослаблением в тропосфере)

расстояние до спутника (стационарная орбита)

Итак множитель ослабления радиоволн на трассе Земля-Космос можно найти из формулы (3.2.4)

(3.2.4)

Для самого худшего случая (сильный дождь)

Принятая мощность с учетом влияния атмосферы

4. Принцип действия ферритового поляризатора.

Действие поляризационного циркулятора основано на использовании поворота плоскости поляризации электромагнитной волны в волноводе с продольно намагниченным ферритовым стержнем.

Ферритовый поляризатор представлен на рисунке 4.1.

Рис. 4.1 Чертеж ферритового поляризатора

Вдоль оси круглого волновода установлен ферритовый стержень круглого сечения, находящийся под воздействием постоянного магнитного поля , направленного вдоль стержня. Такое магнитное поле создается с помощью соленоида, намотанного снаружи круглого волновода. Для уменьшения управляющего постоянного магнитного поля применяются диэлектрические втулки, которые надеваются на ферритовый стержень и значительно увеличивают концентрацию поля в области расположения феррита, что приводит к увеличению угла поворота плоскости поляризации.

Длина ферритового стержня и напряженность постоянного магнитного поля подбираются такими, чтобы плоскость поляризации электромагнитной волны при распространении вдоль стержня повернулась на угол . Направление поворота плоскости поляризации будет зависеть от направления постоянного магнитного поля.

Список использованных источников.

1.Жук М.С., Молочкон Ю.Б. Проектирование антенно-фидерных устройств. –М.1966

2.Зузенко В.А., Кислов А.Г., Цыган Н.Я. Расчет и проектирование антенн.-Л.1969

3.Драбкин А.Л., Зузенко В.Л., Кислов А.Г. Антенно-фидерные устройства.-М1974.

4.Красюк Н.П., Дымович Н.Д.Электродинамика и распространение радиоволн.-М1974