Синтеза и анализ комбинационных схем

Содержание

1. Полный дешифратор с прямыми выходами

2. Полный дешифратор с инверсными выходами

3. Неполный дешифратор (дешифратор кода Джонсона)

4. Шифратор (4-канальный приоритетный шифратор прерываний)

5. Мультиплексор. Мультиплексор-демультиплексор

6. Синтез КС на мультиплексорах (арифметический сумматор)

7. Преобразователь кода Грея в двоичный код 8-4-2-1

8. Узел свертки по четности

Список литературы



1. Полный дешифратор с прямыми выходами

Дешифраторами называются КС, входящие в группу преобразователей кодов. Дешифратор (декодер) преобразует входной n-разрядный двоичный код в унитарный (позиционный) код. В унитарном коде только на одной позиции разряд принимает активное значение: на одной позиции 1, на остальных – 0 (в дешифраторах с прямыми выходами) или на одной позиции 0, на остальных – 1 (в дешифраторах с инверсными выходами).

В зависимости от количества выходов k (количества разрядов в выходном позиционном коде) дешифраторы могут быть полными, неполными или селекторами. Полный дешифратор имеет n входов и k = 2n выходов, неполный – n входов и k < 2n выходов, селектор – n входов и 1 выход.

На рис. 10,а приведена таблица истинности для полного дешифратора 3×8 (3 входа, 8 выходов) с прямыми выходами, на рис.10,б – его условное графическое обозначение в соответствии с ЕСКД, на рис. 10,в – результаты его синтеза на ЛЭ основного базиса.

Из таблицы истинности следует, что дешифратор реализует систему выходных логических функций y>0 >,...,y>7> от входных переменных x>2>, x>1>, x>0>. Каждая функция содержит только одно единичное значение, поэтому ее представление в СДНФ имеет вид y>i> = m>i>. Все реализуемые дешифратором выходные функции приведены на рис. 10,в.

Из сказанного следует, что полный дешифратор на своих выходах реализует полный набор (2n) минтермов. Поэтому дешифратор может быть применен для реализации произвольных ПФ (систем произвольных ПФ). Для этого ПФ представляются в СДНФ через дизъюнкцию соответствующих минтермов.



2. Полный дешифратор с инверсными выходами

На рис.11,а приведена таблица истинности для полного дешифратора 3×8 с инверсными выходами, на рис.11,б его условное графическое обозначение и реализуемые выходные функции. Такой дешифратор реализует на своих выходах полный набор макстермов M>i>, так как все его выходные функции содержат только одно нулевое значение. Дешифратор с инверсными выходами также можно применять для реализации произвольных ПФ, представленных в СКНФ через конъюнкцию макстермов.

Сигнал E для дешифраторов является сигналом разрешения его работы (E=1), если E = 0 – не формируется ни один минтерм (рис.10,б), ни один макстерм (рис.11,б).

3. Неполный дешифратор (дешифратор кода Джонсона)

Приведенные примеры полных дешифраторов показывают, что при получении схем не выполнялась минимизация выходных функций, так как отсутствуют соседние минтермы или макстермы.

Неполный дешифратор формирует неполный набор минтермов (макстермов) – N из возможных 2n для полного дешифратора (N < 2n). Следовательно, в составе наборов входных переменных нет кодовых комбинаций, соответствующих отсутствующим минтермам (макстермам). Отсутствующие кодовые комбинации являются факультативными, что является основанием для минимизации функций выходов дешифратора и может уменьшить сложность схемы неполного дешифратора. В таком случае неполный дешифратор является специализированным преобразователем кода, который для заданных входных кодовых комбинаций формирует соответствующие контермы (дизтермы).

На рис.12 приведен пример синтеза неполного дешифратора для декодирования кода Джонсона. Код Джонсона - специальный цифровой код заданной разрядности n, в котором кодовые комбинации формируются путем “вытеснения” единиц нулями, затем – наоборот (см. пример на рис.12,а для n = 3). Количество комбинаций кода Джонсона N = 2n.

Таблица истинности для рассматриваемого примера (рис.12,а) имеет всего 6 строк, отсутствуют наборы с номерами 2 и 5, которые являются факультативными, и которым в картах Карно для выходных функций дешифратора (рис.12,б) соответствуют клетки, обозначенные знаком ×.

Минимизация по картам Карно выходных функций дешифратора с включением в подкубы факультативных клеток приводит к получению для всех функций контермов второго ранга (вместо минтермов третьего ранга для полного дешифратора). Специализированный дешифратор для декодирования кода Джонсона (рис.12,в) требует меньших аппаратных затрат по сравнению с полным дешифратором 3×23, который тоже можно для этого использовать, задействовав нужные выходы.

4. Шифратор (4-канальный приоритетный шифратор прерываний)

Шифраторами называются КС, входящие в группу преобразователей кодов. Шифратор решает задачу, обратную задаче дешифратора. Шифратор (кодер) преобразует входной унитарный (позиционный) код в выходной двоичный код.

При проектировании микропроцессорных устройств часто возникает ситуация, когда несколько периферийных устройств (ПУ) одновременно хотят связаться с микропроцессором (МП) для того, чтобы выполнить определенные совместные действия (подпрограмму, запрашиваемую ПУ). В этом случае говорят, что ПУ вырабатывает сигнал прерывания с целью прервать текущую работу МП и перейти на подпрограмму обслуживания этого ПУ.

Логической задачей обработки всех запросов прерываний для КС, представленной на рис 13,а, является выработка для МП сигнала INT, если есть хотя бы один запрос I>0>, I>1>, I>2>, I>3> на прерывание от ПУ и получение кода ПУ, сделавшего запрос (адресного кода A>1>A>0>) , по которому МП находит требуемую подпрограмму. При наложении запросов (при совпадении по времени) КС формирует адрес ПУ, имеющего высший приоритет. КС, решающая такую задачу, называется приоритетным шифратором.

Таблица истинности рис.13,б отображает логику работы приоритетного шифратора. Наивысший приоритет имеет запрос I>0>, низший - I>3>. Символ показывает, что запрос низкого приоритета игнорируется при совпадении с запросом более высокого приоритета.

Результаты минимизации логических функций INT,A>1>,A>0> и КС для их реализации на ЛЭ основного базиса приведены на рис. 13,в,г.

5. Мультиплексор. Мультиплексор-демультиплексор

Мультиплексорами называются КС, входящие в группу коммутационных узлов, работающие как переключатели цифровых сигналов. Логику работы мультиплексора раскрывает 4-канальная (4-входовая) механическая модель коммутатора (рис.14,а). Подвижный контакт коммутатора К устанавливается в позицию, задаваемую двухразрядным адресным кодом А>1>, А>0>, и соединяет соответствующий неподвижный контакт с выходом y .

При этом на выход поступает выбранный с помощью адресного кода цифровой сигнал D>i>.

Условное графическое обозначение 4-канального мультиплексора (MUX) приведено на рис.14,б, а на рис.14,в – обобщенная таблица истин- ности, отображающая логику его работы. Структурная формула (рис.14,в) для логической функции выхода мультиплексора y получена из таблицы истинности в СДНФ и представлена затем через минтермы, реализуемые дешифратором 2×22. Структурная схема 4-канального дешифратора, составленная на основе дешифратора, показана на рис.14,г.

Демультиплексор (рис.15) выполняет операцию, обратную операции мультиплексора (рис.14,а), коммутирует сигнал D на один из 2n выходов, где n – разрядность адресного кода выхода y>i>.

В качестве демультиплексора можно использовать полный дешифратор с входом разрешения E (рис.10,б,в). Если подать коммутируемый сигнал D на вход разрешения E (E = D), то на адресуемом выходе дешифратора будет сигнал, эквивалентный сигналу D.

Демультиплексор можно также реализовать на основе использования интегральных схем (рис. 14,д), называемых мультиплексоры-демультиплексоры. В структуру такой схемы входят дешифратор и аналоговые ключи (АК). Аналоговые ключи выполняются по КМОП-технологии и позволяют создавать схемы с двунаправленной передачей сигналов как в аналоговой, так и в цифровой форме. Ключ управляется цифровым сигналом z>i>, переводящим его в замкнутое состояние (z>i> = 1 - сопротивление ключа мало), или разомкнутое (z>i>> >= 0 - сопротивление ключа велико). Для аналоговых ключей входы и выходы неразличимы, поэтому любой вход x>i> может служить выходом, а любой выход y>i>> >- входом.

Мультиплексор-демультиплексор (рис. 14,д) выполняет функцию демультиплексора, если соединить все входы x = x>0> =x>1> = x>2> =x>3> и на объединенный вход x подать сигнал D, тогда выходами являются линии y>0>, y>1>, y>2>, y>3> . Для получения мультиплексора соединяются все выходы, и объединенный выход y = y>0> = y>1> = y>2> = y>3 >является выходом мультиплексора.

6. Синтез КС на мультиплексорах (арифметический сумматор)

Логическая функция, реализуемая мультиплексором (рис.14,в) с n адресными входами, по структуре полностью совпадает с СДНФ для функций n переменных (1). Из этого следует, что любую ПФ n переменных можно реализовать тривиальным прямым способом, подав переменные на адресные входы, а на входы D>i> - константы 0 или 1.

Более эффективен (по критерию затрат аппаратных средств) способ реализации ПФ на основе мультиплексора, когда на информационные входы D>i> подаются не только константы 0 и 1, но и переменные и некоторые функции от переменных, выполняемые простыми ЛЭ (рис.16). В этом случае 4-канальный мультиплексор, имеющий два адресных входа, можно использовать для реализации функции трех переменных y( x>2>,x>1>,x>0 >).

В качестве примера рассмотрим синтез логической схемы одноразрядного арифметического полного сумматора на основе 4-канальных мультиплексоров. Таблица истинности сумматора приведена на рис.17,а. В таблице: a>i> и b>i> – суммируемые разряды, p>i>>-1 >- перенос из (i-1)-го разряда; s>i> - значение суммы; p>i> – перенос из i-го в (i+1)-й разряд.

В СДНФ логическая функция переноса p>i>> >имеет вид:

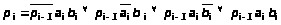. (12)

Примем в качестве адресных переменных A>1>, A>0> соответственно переменные и перепишем уравнение (12) в виде, соответствующем логическому уравнению 4-канального мультиплексора (рис.14,в)

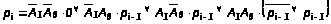. (13)

Из сопоставления уравнения (13) и уравнения 4-канального мультиплексора (рис.14,в) следует: D>0> = 0, D>1> = p>i>>-1>, D>2> = p>i>>-1>, D>3> = () = 1.

Проще и нагляднее получаются функции входов мультиплексора при использовании карт Карно. При сделанном выборе адресных переменных каждому из четырех информационных входов мультиплексора соответствует одна из четырех зон карты Карно, показанных на рис.17,б. Каждую из этих зон можно рассматривать как двухклеточную карту Карно, которая задает логическую зависимость сигнала входа D>i> мультиплексора от переменной p>i>>-1>, не используемой в качестве адресной переменной. Для выявления этой логической связи необходимо сопоставить значения, принимаемые переменной p>i>>-1>, и значения функции (p>i>> >или s>i>> >), записанные в клетках карты. Эти значения либо равны, либо находятся в инверсной связи, либо значение функции не зависит от переменной p>i>>-1> (равно 0 или 1).

Полученные по картам значения функций входов мультиплексоров приведены на рис.17,в,г, а на рис.17,д – соответствующая им структурная схема арифметического сумматора, выполненная на двух мультиплексорах с общими адресными входами. На рис.17,е – условное графическое обозначение одноразрядного арифметического полного сумматора. Многоразрядные арифметические сумматоры (рис.17,ж – арифметический сумматор двух четырехразрядных двоичных чисел) строятся на основе одноразрядных арифметических сумматоров (рис.17,е), на рис.17,з – условное графическое обозначение такого сумматора.

Для функций трех переменных y( x>2>,x>1>,x>0 >) возможны три варианта выбора адресных переменных А>1>,А>0> (рис.18,а). Каждому варианту соответствует свой способ разделения карты Карно на четыре зоны, определяющие логические функции информационных входов D>j> .

На рис.18,б приведены все возможные варианты выбора адресных переменных и разделения карт Карно на зоны, если 4-канальный мультиплексор используется для реализации функции y( x>3>,x>2>,x>1>,x>0 >) четырех переменных.

Выбор адресных переменных должен быть оптимальным, так как сложность функций на информационных входах D>j>> >, а значит и КС в целом, в общем случае зависит от сделанного выбора. Критерием оптимальности выбора адресных переменных может служить количество функций, равных 0 и 1, а также сложность функций, не равных 0 и 1. В качестве адресных сигналов следует использовать те переменные, которые входят в МДНФ наибольшее число раз. В этом случае наибольшую логическую нагрузку будет нести внутренний дешифратор мультиплексора. Такой подход к выбору адресных сигналов позволяет исключить полный перебор всех вариантов.

7. Преобразователь кода Грея в двоичный код 8-4-2-1

Код Грея является циклическим кодом, который используется в системах контроля цифровых устройств, в преобразователях механических перемещений в цифровой код и т.д. Две соседние цифровые комбинации кода Грея отличаются всегда значениями только одного разряда. Такие комбинации образуют цепь длиной 2n, где n – число разрядов в коде Грея.

На рис.19,а показаны кодовые комбинации цепи Грея для n = 2, которые используются для задания координат строк и столбцов карт Карно для ПФ четырех переменных (рис.19,б). Если обойти все клетки карты рис.19,б в направлении стрелки и для каждой клетки записать ее координаты x>3>,x>2>,x>1>,x>0>, получим все (24) комбинации 4-разрядного кода Грея (рис.19,в). Правая часть таблицы содержит все комбинации двоичного кода 8-4-2-1.

Синтезируемый преобразователь должен формировать для каждой комбинации кода Грея соответствующую комбинацию кода 8-4-2-1.Задача синтеза сводится к синтезу системы логических функций y>3>,y>2>,y>1>,y>0> от переменных x>3>,x>2>,x>1>,x>0>. Карты Карно для этих функций позволяют получить структурные формулы для формирования разрядов y>3>,y>2>,y>1>,y>0> выходного кода (рис.19,г). Скобочные преобразования всех полученных по картам исходных формул (МДНФ) с использованием тождеств алгебры логики приводят к логическим выражениям на основе операции (Исключающее ИЛИ):

.

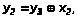
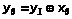Структурная схема преобразователя кода Грея в двоичный код

8-4-2-1 приведена на рис.19,д, а на рис.19,е – условное графическое изображение преобразователей кода.

8. Узел свертки по четности

Сверткой по четности цифрового кода (слова) x>3>,x>2>,x>1>,x>0> называется логическое преобразование вида 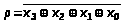. Для n-разрядных кодов преобразование для функции p записывается аналогично. Логическая функция p является признаком четного число единиц в коде. Если число единиц четное, то p = 1, если – нечетное, то p = 0 (в истинности этого утверждения можно убедиться методом перебора вариантов).

Свертка по четности очень часто используется для контроля по четности (контроля по паритету) при передаче цифровых кодов по каналам передачи данных, при чтении их из устройств памяти и т.п. Задача контроля по четности – обнаружение одиночных ошибок в принимаемом из канала связи (или извлекаемом из памяти) коде. Одиночной ошибкой является замена единицы в каком-то одном разряде нулем или - наоборот.

Общая схема организации контроля по четности показана на рис.20. Источник данных для каждой кодовой комбинации (для n-разрядного цифрового слова) формирует признак четности, который в качестве дополнительного (n+1)-го разряда отправляется вместе с передаваемым словом в канал передачи данных. Передаваемое (n+1)-разрядное слово имеет всегда нечетное число единиц. Если в исходном коде число единиц было нечетным, то на выходе КС1 значение контрольного разряда p = 0 не меняет число единиц при передаче слова. Если же число единиц в исходном коде было четным, то контрольный разряд для такого кода p =1, и результирующее число единиц в передаваемом (n+1)-разрядном слове станет нечетным. На приемном конце канала от полученного (n+1)-разрядного слова снова берется свертка по четности e. Если значение этой свертки равно 1, то или в передаваемом слове , или в контрольном разряде при передаче произошла ошибка.

Столь простой контроль не позволяет исправить ошибку, но он дает возможность при обнаружении ошибки исключить неверные слова, затребовав повторную передачу и т.п. Двойную ошибку контроль по четности не обнаруживает.

Развитием принципа контроля по четности являются корректирующие коды, например код Хэмминга, который позволяет не только обнаруживать, но и исправлять одиночную ошибку. Возможность исправления ошибки основывается на повторенной k раз процедуре контроля по четности, но не всего слова сразу, а k определенных групп его разрядов. Слово разбивается на группы так, чтобы номер любого разряда, однозначно определялся по его принадлежности или непринадлежности к этим группам. По номерам групп, в которых обнаружена ошибка, определяется номер искаженного разряда. Исправление ошибки сводится к инвертированию искаженного бита.



Список литературы

1.Пухальский Г.И., Новосельцева Т.Я. Цифровые устройства: Учеб. пособие для втузов. СПб.: Политехника, 1996.

2.Угрюмов Е.П. Цифровая схемотехника. СПб.: БХВ-Петербург, 2001.

3.Проектирование импульсных и цифровых устройств радиотехнических систем: Учеб. пособие для радиотехнич. спец. вузов / Ю.П.Гришин, Ю.М.Казаринов, В.М.Катиков и др.; Под. ред. Ю.М.Казаринова. М.: Высш. шк., 1985.