Синтез системы автоматического управления непрерывным объектом

Содержание

Введение

1 Описание объекта в области z-преобразований, переменных состояний

2 Синтез непрерывного регулятора

3 Синтез компенсатора

4 Синтез дискретного регулятора

5 Синтез дискретного компенсатора

6 Формирование интегрального квадратичного критерия

7 Синтез оптимального закона управления

8 Расчёт релейного регулятора

Заключение

Введение

Задача синтеза возникает при проектировании системы автоматического регулирования. Она заключается в таком выборе структурной схемы и технических средств ее реализации, при котором обеспечиваются требуемые динамические и эксплуатационные свойства всей системы в целом.

Синтез – лишь первый этап проектирования и создания системы.

В зависимости от вида исходных данных, принимаемых при проектировании системы, к задачам синтеза можно подходить с различных точек зрения. Если имеется возможность достаточно полной свободы выбора структуры и параметров в пределах физической реализуемости и с учетом наложенных ограничений, то решается задача синтеза оптимальной системы регулирования.

Оптимальность – наилучшие свойства системы в смысле некоторого критерия оптимальности (например, наилучшее быстродействие).

Задачи синтеза систем регулирования можно разбить на две группы. В задачах первой группы задается только объект управления и требуется определить закон функционирования регулятора в целом. При этом, обычно, предполагается, что полученные при расчетах свойства регулятора могут быть технически реализованы с необходимой точностью. Задачи подобного типа возникают при синтезе систем регулирования промышленных непрерывно функционирующих объектов (химических реакторов, электростанций и пр.).

В задачах второй группы в понятие синтеза вкладывается более узкий смысл. При этом рассматриваются задачи выбора и расчета параметров специальных корректирующих устройств, обеспечивающих заданные статические и динамические характеристики системы. При этом предполагается, что основные функциональные элементы системы (исполнительные, измерительные устройства) уже выбраны в соответствии с техническим заданием и вместе с объектом регулирования представляют собой неизменяемую часть системы. Подобная задача возникает чаще всего при проектировании различного рода следящих систем.

Разработано большое число в основном приближенных методов синтеза корректирующих устройств. Наибольшее распространение получили графоаналитические методы синтеза, основанные на построении инверсных и логарифмических частотных характеристик разомкнутой системы. При этом, используются косвенные оценки качества переходного процесса: запас по модулю, запас по фазе, частота среза, колебательность – которые можно непосредственно определить по частотным характеристикам.

К другой группе относятся аналитические методы синтеза. Для них находится выражение, аналитически связывающее качества с параметрами корректирующего устройства, и определяются значения параметров, соответствующих экстремальному значению функции. К этим методам относится синтез по интегральным критериям качества переходного процесса, а также по критерию среднеквадратичной ошибки.

Задача синтеза противоположна задаче анализа. Если при анализе структура и параметры заданы, а ищут поведение системы в заданных условиях, то в данной задаче задание и цель меняются местами.

Существуют методы синтеза, при которых задается кривая переходного процесса. Но реализация систем с переходным процессом, заданным чрезмерно жестко, как правило, оказывается довольно трудной: система получается неоправданно сложной и зачастую нереализуемой. Поэтому большее распространение получил метод задания более грубых качественных оценок (таких, как перерегулирование, время регулирования, колебательность), при которых сохраняется большая свобода в выборе детальной формы кривой переходного процесса.

Динамические характеристики объектов обычно могут быть аппроксимированы некоторыми типовыми зависимостями. Это позволяет все возможное разнообразие требуемых законов свести к нескольким типовым законам регулирования, которые используются на практике. Следовательно, задача синтеза системы регулирования сводится к выбору подходящего регулятора с типовым законом регулирования и определению оптимальных значений параметров настройки выбранного регулятора.

1. Описание объекта в области z-преобразований, переменных состояний

Анализ дискретных систем существенно упрощается, если величины, описывающие поведение системы, рассматриваются в дискретные моменты времени. Поэтому непрерывная функция времени может быть заменена дискретной, значения которой определены только в дискретные моменты времени.

Для таких функций времени может быть введено понятие дискретного преобразования Лапласа:

которое называется z-преобразованием при подстановке , и связывает изображение с оригиналом.

Рис. 1. Структура системы управления

Преобразование системы в дискретную область и выбор периода квантования будем проводить с помощью Matlab’а.

Чтобы обеспечить заданную погрешность аппроксимации менее 10%, нужно выбрать период квантования так, чтобы он составлял не более 10% от постоянной времени Т.

Также, при выборе преиода квантования нужно учитывать значение запаздывания. Выберем период квантования, равным 0.5.

W1=tf([0.9],[20 1],'td',1) % задаем передаточную функцию

W2=tf([1],[500 100 1],'td',15) % задаем передаточную функцию

Wob=W1*W2 % общая передаточная двух последовательных частей системы

T=0.5 % время квантования

Wdiskr=c2d(Wob,T,'zoh') % передаточная в дискретной области

Получим значение передаточной функции дискретной системы:

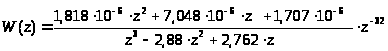
Найдем описание объекта в пространстве состояний с помощью Matlab’а.

W1=tf([0.9],[20 1],'td',1) % задаем передаточную функцию

W2=tf([1],[500 100 1],'td',15) % задаем передаточную функцию

Wob=W1*W2 % общая передаточная двух последовательных частей системы

[A, B, C]=ssdata(Wob) % матрицы в пространстве состояний

Получим значения матриц:

2. Синтез непрерывного регулятора

На практике, применяются следующие регуляторы:

П-регулятор.

Регулятор перемещает регулирующий орган пропорционально отклонению регулируемой величины от заданного значения:

k – коэффициент передачи П-регулятора.

И-регулятор.

Регулятор перемещает регулирующий орган пропорционально интегралу от отклонения регулируемой величины:

Коэффициент пропорциональности k, численно равный скорости перемещения регулирующего органа при отклонении регулируемой величины на единицу ее измерения, называется коэффициентом передачи И-регулятора.

ПИ-регулятор.

Эти регуляторы перемещают регулирующий орган пропорционально сумме отклонения и интеграла от отклонения регулируемой величины:

Постоянная времени Т – постоянная времени интегрирования (время изодрома).

В динамике, ПИ-регулятор соответствует системе из двух параллельно включенных звеньев: пропорционального и интегрирующего.

ПД-регулятор.

Рассматриваемые регуляторы перемещают регулирующий орган пропорционально отклонению и скорости изменения регулируемой величины:

Постоянная времени Т характеризует степень ввода в закон регулирования производной. Она называется постоянной времени дифференцирования (временем предварения регулятора).

В динамическом отношении, эти регуляторы подобны системе из двух параллельно включенных звеньев: безынерционного и идеального диффиренцирующего.

ПИД-регулятор.

В динамическом отношении, эти регуляторы подобны системе из трех параллельно включенных звеньев: безынерционного, интегрирующего и идеального дифференцирующего.

Структура и параметры настройки регуляторов выбираются исходя из динамических или математических моделей объектов.

При определении оптимальных параметров настройки регуляторов промышленных процессов в качестве показателя оптимальности системы регулирования обычно выбирается требование минимума того или иного критерия качества при действии на объект наиболее тяжелого возмущения (или изменении заданного значения регулируемой величины) с учетом добавочного ограничения на запас устойчивости системы.

При практических расчетах запас устойчивости удобно характеризовать показателем колебательности системы, величина которого в системах совпадает с максимумом амплитудно-частотной характеристики замкнутой системы регулирования.

Для заданной системы (Рис. 1.) нужно подобрать регулятор, обеспечивающий желаемый показатель колебательности.

Допустимое значение показателя колебательности М определяется на основании опыта эксплуатации систем регулирования. В хорошо демпфированных системах регулирования показатель колебательности не должен превосходить значений 1,1-1,5. Хотя в некоторых случаях допускается значение 2-2,5.

В нашем случае, М=1,25

Расчет регулятора сводится к следующей методике расчета:

Величина параметра регулятора, при которой амплитудно-фазовая характеристика разомкнутой системы будет касаться окружности с заданным М, определяется следующим образом:

1. Строится АФЧХ регулируемого объекта, и из начала координат проводится луч под углом к отрицательной вещественной полуоси.

2. Проводится окружность с центром на вещественной отрицательной полуоси, касающаяся одновременно АФЧХ регулируемого объекта и этого луча.

В качестве регулятора попробуем использовать ПИ-регулятор. Найдем его параметры с помощью Mat lab’а.

clc

clear

W1=tf([0.9],[20 1],'td', 1) % задаем передаточную функцию

W2=tf([1],[500 100 1],'td', 15) % задаем передаточную функцию

Wob=W1*W2 % общая передаточная двух последовательных частей системы nyquist(Wob)

M=1.25;

w=0.0001:0.0001:0.3;

s=i*w;

Kp=3.2;

Ki=0.03

Wob1=((0.9).*(Kp+(Ki./(s))))./(10000*s.^3+2500*s.^2+120*s+1);

re=real(Wob1);

im=imag(Wob1);

R=M/(M^2-1);

C=(M^2)/(1-M^2);

x=-1:0.00001:0.4;

y1=sqrt(R^2-(x-C).^2);

y2=-sqrt(R^2-(x-C).^2);

K=tan(asin(1/M));

y3=K*x;

plot(re, im, x,y1,x,y2,x,y3)

grid on

Изменяя значения K_>p> и K_>i>, подберем такие значения, при которых окружность одновременно касается АФЧХ и луча. Это достигается при:

Рис. 5. Расчет ПИ-регулятора

Промоделируем систему с и

Рис.6. Структура объекта с регулятором

Получим характеристику:

Рис. 7. Поведение непрерывного объекта с ПИ-регулятором

При использовании данного регулятора точность составит

что удовлетворяет заданному условию

Следовательно будем использовать ПИ-регулятор с параметрами

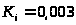
Передаточная функция такого регулятора имеет вид:

3. Синтез компенсатора

Для того, чтобы добиться желаемого качества процесса управления или регулирования (требуемой точности системы и качества переходного процесса), можно изменить структуру системы, введя дополнительные звенья корректирующие устройства (компенсаторы).

Основная задача компенсаторов состоит в улучшении точности системы и качества переходных процессов.

Систему с компенсатором можно представить в виде:

Рис. 8. Система с компенсатором

Рассчитать компенсатор можно следующим образом:

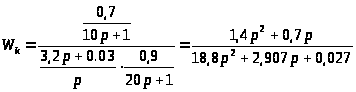
Условие физической реализуемости компенсатора соблюдено – степень числителя не превышает степень знаменателя.

Промоделируем в Simulink систему без учёта компенсатора

Рис. 9. Структура системы без компенсатора

Характеристика системы будет следующей

Рис. 10. Поведение системы без компенсатора

Промоделируем в Simulink систему с учётом компенсатора

Рис. 11. Структура системы с компенсатором

Характеристика системы будет следующей

Рис. 12. Поведение системы с компенсатором

Характеристики систем

Рис. 13.

Из Рис. 13 делаем вывод : компенсатор снизил возникшую при введении в систему внешнего воздействия ошибку.

4. Синтез дискретного регулятора

Предполагается, что ступенчатое изменение задающей переменной происходит в момент времени k=0:

ω(k)=1 для k= 0,1,2,… .

Так как время запаздывания не равно нулю (d≠0), то необходимо использовать следующую модель объекта:

(2.1)

Коэффициенты этой модели удовлетворяют соотношениям:

(2.2)

На процесс управления наложены теперь следующие ограничения:

y(k)=ω(k)=1 для k ≥ ν=m+d,

u(k)=u(m) для k ≥ m.

Тогда параметры регулятора:

(2.3)

Таким образом, получим передаточную функцию апериодического регулятора:

(2.4)

Отсюда следует, что передаточная функция по задающему сигналу при использовании точной модели объекта будет равна:

(2.5)

а ее характеристическое уравнение:

(2.6)

что говорит об апериодическом характере переходного процесса.

Будем рассчитывать регулятор, включенный последовательно с объектом, с помощью Matlab’а.

W1=tf([0.9],[20 1],'td', 1) % задаем передаточную функцию

W2=tf([1],[500 100 1],'td', 15) % задаем передаточную функцию

Wob=W1*W2 % общая передаточная двух последовательных частей системы

T=1 % время квантования

Wdiskr=c2d(Wob,T,'zoh') % передаточная в дискретной области

[Numer Denom]=tfdata(Wdiskr, 'v') % коэффициенты числителя и знаменателя

m=length (Numer)

Denom1=Denom(2:m)

Numer1=Numer(2:m)

q0=1/sum(Numer1)

for i=1:(m-1)

q(i)=q0*Denom1(i)

p(i)=q0*Numer1(i)

end

Q=[q0 q] % матрица коэффициентов числителя

P=[1 -p] % матрица коэффициентов знаменателя

Wr=tf(Q, P, T) % передаточная функция регулятора

Получим значение передаточной функции дискретного регулятора:

Посмотрим на поведение системы при использовании такого регулятора. Промоделируем поведение системы в Simulink’e.

Рис. 12. Структура системы с дискретным регулятором

Получим следующий график:

Рис. 13. Поведение системы с дискретным регулятором

Как видно из полученного графика, установившаяся ошибка и время перерегулирования отсутствует. Время регулирования составляет 3 такта.

Таким образом, произведен синтез дискретного регулятора.

5. Синтез дискретного компенсатора

Систему с компенсатором можно представить в виде:

Рис. 14 Система с компенсатором

Таким образом, рассчитать компенсатор можно следующим образом:

Рассчитаем дискретный компенсатор с помощью Matlab’а.

W1=tf([0.9],[20 1],'td', 1) % задаем передаточную функцию

W2=tf([1],[500 100 1],'td', 15) % задаем передаточную функцию

Wf=tf([0.7],[10 1]) % задаем передаточную функцию

Wob=W1*W2 % общая передаточная двух последовательных частей системы

T=1 % время квантования

Wdiskr=c2d(Wob,T,'zoh') % передаточная в дискретной области

W1d=c2d(W1,T,'zoh') % передаточная в дискретной области

W2d=c2d(W2,T,'zoh') % передаточная в дискретной области

Wfd=c2d(Wf,T,'zoh') % передаточная в дискретной области

[Numer Denom]=tfdata(Wdiskr, 'v') % находим числитель и знаменатель

m=length (Numer)

Denom1=Denom(2:m)

Numer1=Numer(2:m)

q0=1/sum(Numer1)

for i=1:(m-1)

q(i)=q0*Denom1(i)

p(i)=q0*Numer1(i)

end

Q=[q0 q] % матрица коэффициентов числителя

P=[1 -p] % матрица коэффициентов знаменателя

Wr=tf(Q, P, T) % передаточная функция регулятора

Wkomp=(Wfd)/(Wr*W1d) % передаточная функция компенсатора

[Nk Dk]=tfdata(Wkomp, 'v') % коэффициенты числителя и знаменателя

[Nf Df]=tfdata(Wfd, 'v') % коэффициенты числителя и знаменателя

[N1 D1]=tfdata(W1d, 'v') % коэффициенты числителя и знаменателя

[N2 D2]=tfdata(W2d, 'v') % коэффициенты числителя и знаменателя

Получим значение передаточной функции дискретного компенсатора:

Посмотрим на поведение системы при использовании такого компенсатора. Промоделируем поведение системы в Simulink’e.

Рис. 15. Система без компенсатора

Получим следующую характеристику:

Рис. 16. Поведение системы без дискретного компенсатора

С дискретным компенсатором система примет вид:

Рис. 17. Система с компенсатором

И характеристика будет следующей:

Рис. 18. Поведение системы с дискретным компенсатором

Как видно из характеристик, полученный дискретный компенсатор достаточно хорошо компенсирует возмущение.

6. Формирование интегрального квадратичного критерия

Любой критерий оптимальности есть аналитическая оценка оптимизируемого качества системы, зависящая от её параметров, задающих x и возмущающих f воздействий на объект управления u. Таким образом, критерий оптимальности выражается в виде функционала J(u), зависящего от функции управления, а оптимальное управление U_>опт> определяется как функция, реализующая экстремум критерия качества, т. е. функционал J(u).

Изначально объект задан в виде:

Рисунок 19 – Исходная модель объекта

Имеем систему, которая описывается моделью в области переменных состояния:

A, B, S – постоянные матрицы;x – ошибка по каждой из координат и равна:

Необходимо построить систему, которая обеспечит стабилизацию этих координат , т.е. сформировать оптимальный закон управления, минимизирующий функционал качества. Будем использовать квадратичный критерий вида:

Поскольку система имеет не первый порядок, то будем использовать квадратичный функционал, который примет вид:

7.Синтез оптимального закона управления

Для начала необходимо перейти к модели переменных состояний. Для этого необходимо избавиться от запаздывания.

Разобьем запаздывание на 4 равных:

Разложим экспоненту в ряд, ограничиваясь двумя первыми членами:

Таким образом, наше исходное запаздывание можно представить в виде четырех последовательно соединенных блоков и переходить в область переменных состояний от следующей модели:

Рис.20.Вариант системы с учетом возмущающего воздействия и запаздывания

Передаточной функцию второй части объекта, в знаменателе содержит полином второго порядка, представим его в виде произведения двух полиномов первого порядка:

На основе полученных дифференциальных уравнений запишем матрицы A,B,S.

C, D – единичные матрицы, служат в качестве весовых коэффициентов. B – управляющего воздействия, S – матрица возмущающего воздействия.

Функцию φ примем в виде:

где R– положительно определенная симметричная матрица

Воспользуемся уравнением оптимальности Беллмана:

Подставляя производные от φ и в формулу (4.9), получим:

Оптимальный закон управления, минимизирующий выражение в скобках, равен:

Подставляя полученный закон управления в функциональное уравнение Беллмана, и приравнивая коэффициенты при одинаковых степенях переменных состояния, находим уравнения для нахождения матриц Rи L:

Видно, что в первом уравнении системы неизвестной является только матрица R, после её нахождения, на основании второго уравнения системы, можно найти матрицу L, которая представляет собой матрицу коэффициентов обратной связи по возмущению.

И так рассчитаем оптимальный регулятор, для этой цели используем математический пакет MatLab.

clc,clear,echo on

% Расчёт оптимального регулятора

% задание матрицы коэффициентов при переменных состояния

clc

clear

A=[-0.045 0 0 0 0 0 0 0 0;1 -1 0 0 0 0 0 0 0;0 0 -0.07 0 0 0 0 0 0;0 0.01 0.01 -0.01 0 0 0 0 0;0 0 0 0.18 -0.18 0 0 0 0;0 0 0 0 0.26 -0.26 0 0 0;0 0 0 0 0 0.26 -0.26 0 0;0 0 0 0 0 0 0.26 -0.26 0;0 0 0 0 0 0 0 0.26 -0.26];

B =zeros(9)

B(1,1)=0.045;

C=eye(9);

S=zeros(9);

S(3,1)=0.07;

D=eye(9);

R=0.5*eye(9);

Q=R;

% решение уравнения Рикатти

[X,L,G,RR]=care(A,B,Q)

% матрица коэффициентов обратной связи по возмущению

L=G*S*(-G*B-A')

В результате получаем коэффициенты обратной связи по переменным состояния:

G_>1>= 0.5089 G_>5>= 0.0139 G_>9>= 0.0001

G_>2>= 0.0175 G_>6>= 0.0033

G_>3>= 0.0968 G_>7>= 0.0012

G_>4>= 0.6909 G_>8>= 0.0003

Матрица L имеет вид

Построим модель для проверки работы рассчитанного регулятора.

Рис.21. Модель системы с оптимальным регулятором

Получим следующий график переходного процесса:

Рис.22.

Из рисунка можно сделать заключение о том, что регулятор осуществляет качественное управление, так как обеспечивает незначительную статическую ошибку (ε = 0.03).

8. Расчёт релейного регулятора

Реальные автоматические системы требуют при рассмотрении учитывать всякого рода нелинейности. Для элементов, содержащих нелинейности, не выполняется принцип суперпозиции. Это, в свою очередь, ограничивает возможность применения преобразования Лапласа и Фурье.

Нелинейная система – система, содержащая хотя бы одно нелинейное звено, т. е. описываемое нелинейным уравнением. Особые свойства нелинейных систем широко используются в технике. На этих свойствах основано генерирование электромагнитных колебаний, выпрямление переменного тока, умножение и деление частот. По динамическим качествам нелинейные автоматические системы во многих случаях превосходят линейные системы.

Простейшим видом нелинейных корректирующих звеньев являются корректирующие звенья с нелинейной статической характеристикой.

Если пользоваться частотным описанием таких нелинейных динамических корректирующих звеньев (на основе гармонической линеаризации), то их назначение можно определить следующим образом. Во-первых, они применяются для получения определенной желаемой зависимости частотных характеристик от амплитуды сигнала и тем самым для получения различной реакции системы на воздействие разной величины или, наоборот, для устранения нежелательных таких зависимостей, обусловленных имеющимися в системе нелинейностями основных звеньев. Во-вторых, такие корректирующие звенья применяются для преодоления той жесткой зависимости между амплитудной и фазовой частотными характеристиками, которая существует в линейных системах, с целью независимой корректировки каждой из этих характеристик.

Расчет системы с учётом нелинейного элемента:

Заменим в системе ПИ-регулятор на нелинейный элемент. В качестве нелинейного элемента возьмём идеальное реле, статическая характеристика звена изображена на рисунке 23.

Рис.23. Идеальное реле

Чтобы реализовать данный регулятор в заданной системе автоматического управления, требуется рассчитать значения параметра с.

Проанализируем работу системы с нелинейной характеристикой и без неё в Simulink, а затем найдём параметры которые наиболее оптимально обеспечивают качество переходного процесса. На вход системы будем подавать единичное ступенчатое воздействие:

Рис.24. Сравнение работы нелинейной системы с исходной

Получим следующие графики

Рис.25. Работа системы с релейным регулятором и без него

Из переходных характеристик видно, что переходный процесс не выходит на установившееся значение равное единице. Следовательно надо подобрать значение параметра , удовлетворяющее данному условию, а также учесть амплитуду автоколебаний возникающих при желаемом параметре .

Для нахождения значений параметра будем использовать графический метод гармонической линеаризации. Периодическое решение линеаризованной системы получается при наличии в характеристическом уравнении замкнутой системы пары чисто мнимых корней. Тогда в соответствии с критерием Найквиста можно записать:

Применительно к нашему нелинейному элементу передаточная функция, полученная путём гармонической лианеризации, будет иметь следующий вид:

где , а

Построим амплитудно-фазовую характеристику заданной разомкнутой системы в комплексной плоскости. Графическую зависимость, которая соответствует идеальному релейному регулятору, можно и не строить, т.к. передаточная функция идеального реле не содержит мнимых составляющих. Следовательно графическая зависимость будет линейно проходить вдоль вещественной оси координат.

clc;clear;cla;

A=0:0.001:5;

C=0:0.001:5;

Wnon1=4*C./3.14.*A

Z=-1./Wnon1;

Re=real(Z);Im=imag(Z);

W1=tf([0.9],[20 1],'td',1);

W12=tf([1],[500 100 1],'td',15);

W2=W1*W12

figure(1);nyquist(W2);

hold on

figure(1);plot(Re,Im)

Рис. 26 Анализ точки пересечения АФЧХ линейной и нелинейной части системы

Из рис 26. мы определяем координату по вещественной оси точки пересечения амплитудно-фазовой характеристики линейной части и графической зависимости нелинейной части системы управления:

В соответствии с критерием Найквиста

Рассчитаем параметр с:

Амплитуду гармонических колебаний принимаем равным значению желаемой установившейся ошибки. После расчёта получаем значение параметра

Построим в Simulink релейный регулятор с найденными параметрами

clc;

clear;

c=0.177;

C1=1/0.9+c;

C2=1/0.9-c;

Рис.27. Моделирование нелинейного регулятора

Получим следующий график

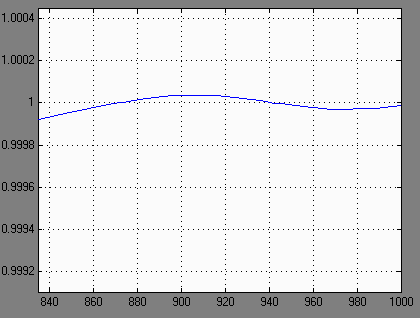
Рис.28. Переходный процесс при использовании нелинейного регулятора

Как видно из графика переходного процесса: имеют место устойчивые автоколебания, амплитуда которых не превышает значения установившейся ошибки равной 3%, заданной по заданию. Следовательно, полученный регулятор на основе нелинейного звена удовлетворяет заданным условиям.

Структура объекта с регулятором

Структура системы без компенсатора

Характеристика системы будет следующей:

Поведение системы без компенсатора

Структура системы с компенсатором

Характеристика системы будет следующей:

Поведение системы с компенсатором

Структура системы с дискретным регулятором

Получим следующий график:

Поведение системы с дискретным регулятором

Система без дискретного компенсатора

Получим следующую характеристику:

Поведение системы без дискретного компенсатора

Система с дискретным компенсатором

Характеристика будет следующей

Поведение системы с дискретным компенсатором

Модель системы с оптимальным регулятором

Получим следующий график переходного процесса

Моделирование нелинейного регулятора

Переходный процесс при использовании нелинейного регулятора

Заключение

В данной курсовой работе был выполнен расчет дискретного регулятора, обеспечивающего максимальную скорость переходного процесса. Предварительно система была переведена в дискретный вид.

Далее был рассчитан дискретный компенсатор возмущающего воздействия. Для системы также был разработан оптимальный регулятор по переменным состояния и рассчитан наблюдатель состояния этих переменных.

Следует отметить, что оптимальные системы крайне чувствительны к возмущениям, кроме того, наблюдатель должен обладать быстродействием в 2-4 раза более высоким, чем остальная часть системы, что не позволяет реализовать его для высокоскоростных процессов. По этим причинам на практике оптимальные системы реализуются лишь частично.

Отметим также, что в настоящее время для целей синтеза систем автоматического регулирования используются электронные вычислительные машины, позволяющие производить полное или частичное моделирование проектируемой системы. Кроме того, все современные системы управления, в следствии всё возрастающих вычислительных и логических возможностей современных микропроцессоров, выполняются на останове цифровой техники.