Визначення і способи задання групових кодів
Зміст
Вступ
Елементи теорії кодування
Відстань Хеммінга
Матричне кодування
Групові коди
Досконалі і квазідосконалі коди
Висновки
Література
Вступ
Використання електронно-обчислювальних машин для переробки інформації з'явилося корінним етапом у вдосконаленні систем планування і управління на всіх рівнях народного господарства. Проте при цьому, на відміну від звичайних способів збору і обробки інформації, виникли проблеми перетворення інформації в символи, зрозумілі для машини. Невід'ємним елементом цього процесу є кодування інформації.
У теорії передачі інформації надзвичайно важливим є вирішення проблеми кодування і декодування, що забезпечує надійну передачу по каналах зв'язку з «шумом».
Метою даної роботи є розглянути деякі питання кодування інформації по каналах зв'язку з перешкодами.
Елементи теорії кодування
Передача інформації зводиться до передачі по якомусь каналу зв'язку символів деякого алфавіту. Проте в реальних ситуаціях сигнали при передачі практично завжди можуть спотворюватися, і переданий символ сприйматиметься неправильно. Наприклад, в системі ЕОМ → ЕОМ одна з обчислювальних машин може бути пов'язана з іншою через супутник. Канал зв'язку в цьому випадку фізично реалізується електромагнітним полем між поверхнею Землі і супутником. Електромагнітні сигнали, накладаючись на зовнішнє поле, можуть спотворитися і ослабитися. Для забезпечення надійності передачі інформації в таких системах розроблені ефективні методи, що використовують коди різних типів.
Одна з таких моделей зв’язана з груповими кодами.
Алфавіт, в якому записуються повідомлення, вважаємо за той, що складається з двох символів {0, 1}. Він називається двійковим алфавітом. Тоді повідомлення є кінцева послідовність символів цього алфавіту. Повідомлення, що треба передати, кодується по певній схемі довшою послідовністю символів в алфавіті {0, 1}. Ця послідовність називається кодом або кодовим словом. При прийомі можна виправляти або розпізнавати помилки, що виникли при передачі по каналу зв'язку, аналізуючи інформацію, що міститься в додаткових символах. Прийнята послідовність символів декодується по певній схемі в повідомлення, з великою вірогідністю співпадаюче з переданим.
Блоковий двійковий (m, n) -код визначається двома функціями: E:{0,1}m - {0, 1}n і D: {0, 1}n - {0, 1}m, де m . n і {0, 1}n - безліч всіх двійкових послідовностей довжини n. Функція E визначає схему кодування, а функція D - схему декодування. Математичну модель системи зв'язку можна представити у вигляді схеми (мал. 1):

Малюнок 1 – Модель системи зв'язку.
Тут T - «функція помилок» ; E і D вибираються так, щоб композиція D T E була функцією, з великою вірогідністю близькою до тотожної. Двійковий (m, n) -код містить 2m кодових слів.
Коди діляться на два великі класи: коди з виявленням помилок, які з великою вірогідністю визначають наявність помилки в прийнятому повідомленні, і коди з виправленням помилок, які з великою вірогідністю можуть відновити послане повідомлення.
Відстань Хеммінга
На безлічі двійкових слів довжини m відстанню d(а, b) між словами а і b називають число неспівпадаючих позицій цих слів, наприклад: відстань між словами а = 01101 і b = 00111 рівне 2.
Визначене таким чином поняття називається відстанню Хеммінга. Воно задовольняє наступним аксіомам відстаней:
1) d(а, b) 0 і d(а, b)= 0 тоді і тільки тоді, коли а = b;
2) d(а, b)= d(b, а);
3) d(а, b)+ d(b, з) d(а, з) (нерівність трикутника).
Вагою w(a) слова а називають число одиниць серед його координат. Тоді відстань між словами а і b є вага їх суми а b: d(а, b)= w(а b), де символом позначена операція покоординатного складання по модулю 2.
Інтуїтивно зрозуміло, що код тим краще пристосований до виявлення і виправлення помилок, чим більше розрізняються кодові слова. Поняття відстані Хеммінга дозволяє це уточнити.
Теорема. Для
того, щоб код дозволяв виявляти помилки
(або менш) позиціях, необхідно і достатньо,
щоб найменша відстань між кодовими
словами була
 k
+ 1.
k
+ 1.
Доведення цієї теореми аналогічно доказу наступного твердження.
Теорема. Для
того, щоб код дозволяв виправляти всі
помилки (або менш) позиціях, необхідно
і достатньо, щоб найменша відстань між
кодовими словами була
 2k + 1.
2k + 1.
У математичній моделі кодування і декодування зручно розглядати рядки помилок. Дане повідомлення a = a>1>a>2> ...a>m> кодується кодовим словом b= b>1>b>2>...b>n>.. При передачі канал зв'язку додає до нього рядок помилок e=e>1>e>2>...e>n>,, отже приймач приймає сигнал c = c>1>c>2>...c>n>, , де c>i >= b>i> + e>i>.. Система, що виправляє помилки, переводить слово c>1>c>2>...c>n> у найближче кодове слово b>1>b>2> ...b>n>.. Система, що виявляє помилки, тільки встановлює, чи є прийняте слово кодовим чи ні. Останнє означає, що при передачі відбулася помилка.
Ідею представлення код, що коректують, можна представити за допомогою N-вимірного куба.
Візьмемо тривимірний куб (мал. 2), довжина ребер, в якому дорівнює одній одиниці. Вершини такого куба відображають двійкові коди. Мінімальна відстань між вершинами визначається мінімальною кількістю ребер, що знаходяться між вершинами. Ця відстань називається кодовою (або хемінговою) і позначається буквою d.

Малюнок 2 – Представлення двійкових код за допомогою куба
Інакше, кодова відстань - це те мінімальне число елементів, в яких одна кодова комбінація відрізняється від іншої. Для визначення кодової відстані досить порівняти дві кодові комбінації по модулю 2. Так, склавши дві комбінації
10110101101
11001010101
01111111000
визначимо, що відстань між ними d=7.
Для коду з N=3 вісім кодових комбінацій розміщуються на вершинах тривимірного куба. Такий код має кодову відстань d=1, і для передачі використовуються всі вісім кодових комбінацій 000,001..,111. Такий код є не перешкодостійким, він не в змозі виявити помилку.
Якщо виберемо комбінації з кодовою відстанню d=2, наприклад, 000,110,101,011, то такий код дозволить виявляти одноразові помилки. Назвемо ці комбінації дозволеними, призначеними для передачі інформації. Всі останні 001,010,100,111 - заборонені.
Будь-яка одиночна помилка приводить до того, що дозволена комбінація переходить в найближчу, заборонену комбінацію (див. мал. 2). Отримавши заборонену комбінацію, ми виявимо помилку. Виберемо далі вершини з кодовою відстанню d=3

Такий код може виправити одну одиночну помилку або виявити дві помилки. Таким чином, збільшуючи кодову відстань можна збільшити перешкодостійкість коди. У загальному випадку кодова відстань визначається по формулі
d=t + l + 1
де t - число помилок, що виправляються, l - число помилок, що виявляються. Зазвичай l>t.
Більшість кодів, що коректують, утворюються шляхом додавання до початкової k - комбінації r - контрольних символів. У результаті в лінію передаються n=k+r символів. При цьому коди, що коректують, називаються (n,k) кодами. Як можна визначити необхідне число контрольних символів?
Для побудови коди
здатного виявляти і виправляти одиночну
помилку необхідне число контрольних
розрядів складатиме
 .
Це рівносильно відомому завданню про
мінімум числа контрольних питань, на
які можуть бути даны відповіді вигляду
“та чи ні”, для однозначного визначення
одного з елементів кінцевої множини.
.
Це рівносильно відомому завданню про
мінімум числа контрольних питань, на
які можуть бути даны відповіді вигляду
“та чи ні”, для однозначного визначення
одного з елементів кінцевої множини.
Якщо необхідно виправити
дві помилки, то число різних результатів
складатиме
 Тоді
Тоді
 ,
в цьому випадку виявляються одноразові
і двократні помилки. У загальному
випадку, число контрольних символів
має бути не менше
,
в цьому випадку виявляються одноразові
і двократні помилки. У загальному
випадку, число контрольних символів
має бути не менше

Ця формула називається нерівністю Хеммінга, або нижньою межею Хеммінга для числа контрольних символів.
Матричне кодування
При явному завданні схеми кодування в (m, n) -коде слід вказати 2m кодових слів, що вельми неефективно.
Одним з економних способів опису схеми кодування є методика матричного кодування.
Хай  - матриця порядку m f n з елементами e>ij>,
рівними 0 або 1. Символ + позначає складання
по модулю 2. Тоді схема кодування задається
системою рівнянь
- матриця порядку m f n з елементами e>ij>,
рівними 0 або 1. Символ + позначає складання
по модулю 2. Тоді схема кодування задається
системою рівнянь

або в матричній формі b = aЕ, де a = a>1>a>2>...a>m> - вектор, відповідний передаваному повідомленню; b = b>1>b>2>...b>n> - вектор, відповідний кодованому повідомленню; Е - матриця коду, що породжує.
Матриця коду, що породжує, визначена неоднозначно. Код не повинен приписувати різним словам-повідомленням одне і те ж кодове слово. Можна довести, що цього не відбудеться, якщо перші m стовпців матриці Е утворюють одиничну матрицю.
Замість 2m кодові слова досить знати m слів, що є рядками матриці Е.
Групові коди
Безліч всіх двійкових слів a=a>1> … a>m> довжини m утворює абелеву (комутативну) групу щодо порозрядного складання.
Хай E - кодуюча
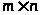 -матрица, у якої є
-матрица, у якої є
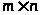 -підматриця з відмінним від нуля
визначником, наприклад, одинична. Тоді
відображення
-підматриця з відмінним від нуля
визначником, наприклад, одинична. Тоді
відображення
 переводить групу всіх двійкових слів
довжини m в групу кодових слів довжини
n.
переводить групу всіх двійкових слів
довжини m в групу кодових слів довжини
n.
Припустимо, що
 .
.
Тоді для b=b>1>…b>n>=aE,
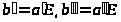 ,
отримуємо
,
отримуємо

тобто
 . Отже, взаємно-однозначне відображення
групи двійкових слів довжини m за
допомогою заданої матриці E зберігає
властивості групової операції, що
означає, що кодові слова утворюють
групу.
. Отже, взаємно-однозначне відображення
групи двійкових слів довжини m за
допомогою заданої матриці E зберігає
властивості групової операції, що
означає, що кодові слова утворюють
групу.
Блоковий код називається груповим, якщо його кодові слова утворюють групу.
Більшість код, що коректують, є лінійними кодами. Лінійні коди - це такі коди, у яких контрольні символи утворюються шляхом лінійної комбінації інформаційних символів. Крім того, що коректують коди є груповими кодами. Групові коди (G>n>) - це такі коди, які мають одну основну операцію. При цьому, повинна дотримуватися умова замкнутості (тобто, при складанні двох елементів групи виходить елемент що належить цій же групі). Число розрядів в групі не повинне збільшуватися. Цій умові задовольняє операція порозрядного складання по модулю 2. У групі, крім того, має бути нульовий елемент.
Наприклад, нижче приведені кодові комбінації, що є групою чи ні.
1) 1101 1110 0111 1011 – не група, оскільки немає нульового елементу
2) 0000 1101 1110 0111 – не група, оскільки не дотримується умова замкнутості (1101+1110=0011)
3) 000 001 010 011 100 101 110 111 - група
4) 000 001 010 111 - підгрупа
Якщо код є груповим, то найменша відстань між двома кодовими словами дорівнює найменшій вазі ненульового слова.
Це витікає із
співвідношення
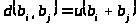 .
.
При використанні групової коди непоміченими залишаються ті і лише ті помилки, які відповідають рядкам помилок, в точності рівним кодовим словам.
Такі рядки помилок переводять одне кодове слово в інше.
Отже, вірогідність того, що помилка залишиться невиявленою, дорівнює сумі вірогідності всіх рядків помилок, рівних кодовим словам.
Розглянемо завдання
оптимізації декодування групової коди
з двійковою матрицею кодування Е.
Требуєтся мінімізувати вірогідність
того, що
 .
.
Схема декодування
складається з групи G всіх слів, які
можуть бути прийняті (#G=2n).
Оскільки кодові слова B утворюють
нормальну (нормальність виходить з
комутативності G) підгрупу G, то безлічі
G можна додати структуру таблиці:
записуватимемо в один рядок ті елементи
G, які є членами одного суміжного класу
G по B. Перший рядок, відповідний нульовому
слову з G, буде тоді всіма кодовими
словами з B, тобто
 .
У загальному випадку, якщо
.
У загальному випадку, якщо
 ,
то рядок, що містить g>i>
(суміжний клас g>i>B
), має вигляд
,
то рядок, що містить g>i>
(суміжний клас g>i>B
), має вигляд
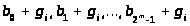 .
.
Лідером кожного з таких побудованих суміжних класів називається слово мінімальної ваги.
Кожен елемент g з G
однозначно представляється у вигляді
суми g>i>+b>j>
де
 - лідер відповідного суміжного класу і
- лідер відповідного суміжного класу і
 .
.
Безліч класів суміжності групи утворюють чинник-групу, яка є чинник-множина безлічі G по відношенню еквівалентності-приналежності до одного суміжного класу, а це означає, що множини, складові це чинник-множина, утворюють розбиття G. Звідси витікає, що рядки побудованої таблиці попарно або не перетинаються, або збігаються.
Якщо в даній таблиці в першому стовпці записати лідери, то отримана таблиця називається таблицею декодування. Вона має вигляд:

Те, що рядків буде 2n-m виходить з теореми Лагранжа1), оскільки 2n-m - це порядок фактор-группы G/B #(G/B)=#(G)/#(B), #B=2m.
Декодування слова g=b>j>+g>i> полягає у виборі кодового слова b>j> як переданий і подальшому застосуванні операції, зворотної множенню на E. Така схема декодування зможе виправляти помилки.
Для (3,6) -кода з даного прикладу таблиця декодування буде наступною:
|
000000 |
100110 |
010011 |
110101 |
001111 |
101001 |
011100 |
111010 |
|
100000 |
000110 |
110011 |
010101 |
101111 |
001001 |
111100 |
011010 |
|
010000 |
110110 |
000011 |
100101 |
011111 |
001101 |
001100 |
101010 |
|
001000 |
101110 |
011011 |
111101 |
000111 |
100001 |
010100 |
110010 |
|
000100 |
100010 |
010111 |
110001 |
001011 |
101101 |
011000 |
111110 |
|
000010 |
100100 |
010001 |
110111 |
001101 |
101011 |
011110 |
111000 |
|
000001 |
100111 |
010010 |
110100 |
001110 |
101000 |
011101 |
111011 |
|
000101 |
100011 |
010110 |
11000 |
001010 |
101100 |
011001 |
111111 |
Перший рядок в ній - це рядок кодових слів, а перший стовпець - це лідери.
Щоб декодувати слово b>j>+e, слід відшукати його в таблиці і вибрати як переданого слово в тому ж стовпці і в першому рядку.
Наприклад, якщо прийнято слово 110011 (2-й рядок, 3-й стовпець таблиці), то вважається, що було передане слово 010011; аналогічно, якщо прийнято слово 100101 (3-й рядок, 4-й стовпець таблиці), за передане вважається слово 110101, і так далі
Групове кодування з схемою декодування за допомогою лідерів виправляє всі помилки, рядки яких збігаються з лідерами. Отже, вірогідність правильного декодування переданої по двійковому симетричному каналу коди дорівнює сумі вірогідності всіх лідерів, включаючи нульовий.
У розглянутій схемі вірогідність правильної передачі слова буде
p6+6p5q+p4q2.
Кодове слово будь-якого стовпця таблиці декодування є найближчим кодовим словом до всіх інших слів даного стовпця.
Хай передане слово b>i> прийняте як b>i>+e, d(b>i>,b>i>+e)=u(e), тобто ця відстань дорівнює вазі відповідного лідера. Відстань від b>i>+e до будь-якого іншого кодового слова b>j> дорівнює вазі їх порозрядної суми, тобто

оскільки e- лідер суміжного класу, до якого належать як b>k>+e, так і b>i>+e.
Доведено, при схемі декодування лідерами по отриманому слову береться найближче до нього кодове.
Досконалі і квазідосконалі коди
Груповий
 -код, що виправляє всі помилки ваги, не
більшої k, і ніяких інших, називається
досконалим.
-код, що виправляє всі помилки ваги, не
більшої k, і ніяких інших, називається
досконалим.
Властивості досконалого коду:
Для досконалого
 -кода, що виправляє всі помилки ваги,
не більшої k, виконується співвідношення
-кода, що виправляє всі помилки ваги,
не більшої k, виконується співвідношення
 . Вірно і зворотне твердження;
. Вірно і зворотне твердження;
Досконалий код, що виправляє всі помилки ваги, не більшої k, в стовпцях таблиці декодування містить всі слова, віддалені від кодових на відстані, не більшому k. Вірно і зворотне твердження;
Таблиця декодування досконалого коду, що виправляє всі помилки в не більше ніж k позиціях, має як лідерів всі рядки, що містять не більш k одиниць. Вірно і зворотне твердження.
Досконалий код - це
кращий код, що забезпечує максимум
мінімальної відстані між кодовими
словами при мінімумі довжини кодових
слів. Досконалий код легко декодувати:
кожному отриманому слову однозначно
ставиться у відповідність найближчу
кодову. Чисел m, n і
 ,
що задовольняють умові досконалості
коди, дуже мало. Але і при підібраних m,
n і k досконалий код можна побудувати
тільки у виняткових випадках.
,
що задовольняють умові досконалості
коди, дуже мало. Але і при підібраних m,
n і k досконалий код можна побудувати
тільки у виняткових випадках.
Якщо m, n і k не задовольняють умові досконалості, то кращий груповий код, який їм відповідає, називається квазідосконалим, якщо він виправляє всі помилки кратності, не більшої k, і деякі помилки кратності k+1. Квазідосконалі код також дуже мало.
Двійковий блоковий
 -код називається оптимальним, якщо він
мінімізує вірогідність помилкового
декодування. Досконалий або квазідосконалий
код - оптимальний. Загальний спосіб
побудови оптимальних код поки невідомий.
-код називається оптимальним, якщо він
мінімізує вірогідність помилкового
декодування. Досконалий або квазідосконалий
код - оптимальний. Загальний спосіб
побудови оптимальних код поки невідомий.
Для будь-якого цілого
позитивного числа r існує досконалий
 -код, що виправляє одну помилку, званий
кодом Хеммінга (Hamming), в якому
-код, що виправляє одну помилку, званий
кодом Хеммінга (Hamming), в якому
 і
і
 .
.
Дійсно
 .
.
Порядок побудови коди Хеммінга наступний:
Вибираємо ціле
позитивне число r. Повідомлення будуть
словами довжини
 ,
а кодові слова - довжини
,
а кодові слова - довжини
 ;
;
У кожному кодовому
слові
 r біт з індексами-ступенями двійки
r біт з індексами-ступенями двійки
 - є контрольними, останні - в природному
порядку - бітами повідомлення. Наприклад,
якщо r=4, то биті
- є контрольними, останні - в природному
порядку - бітами повідомлення. Наприклад,
якщо r=4, то биті
 - контрольні, а
- контрольні, а
 - з початкового повідомлення;
- з початкового повідомлення;
Будується матриця M
з
 рядків і r стовпців. У i-ому рядку стоять
цифри двійкового представлення числа
i. Матриці для r=2, 3 і 4 такі:
рядків і r стовпців. У i-ому рядку стоять
цифри двійкового представлення числа
i. Матриці для r=2, 3 і 4 такі:

Записується система рівнянь bM=0, де M - матриця з попереднього пункту. Система складається з r рівнянь. Наприклад, для r=3

Щоб закодувати повідомлення а, беруться як b>j>, j не дорівнює ступеню двійки, відповідні біти повідомлення і відшукуються, використовуючи отриману систему рівнянь, ті b>j>, для яких j- ступінь двійки. У кожне рівняння входить тільки одне b>j,> j=2j. У виписаній системі b>4> входить в 1-е рівняння, b>2> - в друге і b>1> - в третє. У розглянутому прикладі повідомлення a=0111 буде закодовано кодовим словом b=0001111.
Декодування коду Хеммінга проходить за наступною схемою. Хай прийнято слово b+e, де b - передане кодове слово, а e - рядок помилок. Оскільки bM=0, то (b+e) M=bM+eM=eM. Якщо результат нульовий, як відбувається при правильній передачі, вважається, що помилок не було. Якщо рядок помилок має одиницю в і -ій позиції, то результатом множення eM буде i-й рядок матриці M або двійкове представлення числа i. В цьому випадку слід змінити символ в i-й позиції слова
Код Хеммінга - це
груповий код. Це витікає з того, що (m, n)
-код Хеммінга можна отримати матричним
кодуванням, за допомогою
 -матрицы, в якій стовпці з номерами не
ступенями 2 утворюють одиничну підматрицю.
Решта стовпців відповідає рівнянням
кроку 4 побудови коди Хеммінга, тобто
1-у стовпцю відповідає рівняння для
обчислення 1-го контрольного розряду,
2-у - для 2-го, 4-у - для 4-го і так далі Така
матриця при кодуванні копіюватиме біти
повідомлення у позиції не ступеня 2 коди
і заповнювати інші позиції коди згідно
схемі кодування Хеммінга.
-матрицы, в якій стовпці з номерами не
ступенями 2 утворюють одиничну підматрицю.
Решта стовпців відповідає рівнянням
кроку 4 побудови коди Хеммінга, тобто
1-у стовпцю відповідає рівняння для
обчислення 1-го контрольного розряду,
2-у - для 2-го, 4-у - для 4-го і так далі Така
матриця при кодуванні копіюватиме біти
повідомлення у позиції не ступеня 2 коди
і заповнювати інші позиції коди згідно
схемі кодування Хеммінга.
До (m, n) -коду Хеммінга можна додати перевірку парності. Вийде (m, n+1) -код з найменшою вагою ненульового кодового слова 4, здатний виправляти одну і виявляти дві помилки.
Коди Хеммінга накладають обмеження на довжину слів повідомлення: ця довжина може бути тільки числами вигляду 2r-r-1: 1, 4, 11, 26, 57 . . Але в реальних системах інформація передається байтам або машинними словами, тобто порціями по 8, 16, 32 або 64 бита, що робить використання досконалих кодів не завжди відповідним. Тому в таких випадках часто використовуються квазідосконалі коди.
Квазідосконалі (m, n)
-коды, що виправляють одну помилку,
будуються таким чином. Вибирається
мінімальне n так, щоб

Кожне кодове слово такої коди міститиме k=n-m контрольних розрядів. З попередніх співвідношень виходить, що

Кожному з n розрядів
привласнюється зліва-направо номер від
1 до n. Для заданого слова повідомлення
складаються k контрольних сум S>1>,…,S>k>
по модулю 2 значень спеціально вибраних
розрядів кодового слова, які поміщаються
в позиції-ступені 2 в ньому: для
 вибираються розряди, що містять біти
початкового повідомлення, двійкові
числа-номери яких мають в i-м розряді
одиницю. Для суми S>1>
це будуть, наприклад, розряди 3, 5, 7 і так
далі, для суми S>2>
- 3, 6, 7 і так далі Таким чином, для слова
повідомлення a=a>1>…a>m>
буде побудовано кодове слово
b=S>1>S>2>a>1>S>3>a>2>a>3>a>4>S>4>a>5>...a>m>..
Позначимо через
вибираються розряди, що містять біти
початкового повідомлення, двійкові
числа-номери яких мають в i-м розряді
одиницю. Для суми S>1>
це будуть, наприклад, розряди 3, 5, 7 і так
далі, для суми S>2>
- 3, 6, 7 і так далі Таким чином, для слова
повідомлення a=a>1>…a>m>
буде побудовано кодове слово
b=S>1>S>2>a>1>S>3>a>2>a>3>a>4>S>4>a>5>...a>m>..
Позначимо через
 суму по модулю 2 розрядів отриманого
слова, відповідних контрольній сумі S>i>
і самій цієї контрольної суми. Якщо
суму по модулю 2 розрядів отриманого
слова, відповідних контрольній сумі S>i>
і самій цієї контрольної суми. Якщо
 ,
то вважається, що передача пройшла без
помилок. У разі одинарної помилки
,
то вважається, що передача пройшла без
помилок. У разі одинарної помилки
 дорівнюватиме двійковому числу-номеру
збійного біта. У разі помилки, кратності
більшої 1, коли
дорівнюватиме двійковому числу-номеру
збійного біта. У разі помилки, кратності
більшої 1, коли
 ,
її можна виявити. Подібна схема декодування
не дозволяє виправляти деякі подвійні
помилки, чого можна було б досягти,
використовуючи схему декодування з
лідерами, але остання значно складніше
в реалізації і дає незначне поліпшення
якості коди.
,
її можна виявити. Подібна схема декодування
не дозволяє виправляти деякі подвійні
помилки, чого можна було б досягти,
використовуючи схему декодування з
лідерами, але остання значно складніше
в реалізації і дає незначне поліпшення
якості коди.
Приклад побудови кодового слова квазідосконалого (9, n) -кода, що виправляє всі одноразові помилки, для повідомлення 100011010.

Шукане кодове слово має вигляд
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
S>1> |
S>2> |
1 |
S>3> |
0 |
0 |
0 |
S>4> |
1 |
1 |
0 |
1 |
0 |
Далі потрібно обчислити контрольні суми.

Таким чином, шуканий код - 0011000111010. Якщо в процесі передачі цієї коди буде зіпсований його п'ятий біт, то приймач отримає код 0011100111010. Для його декодування знову обчислюються контрольні суми:

Приймач перетворить зміною п'ятого біта отримане повідомлення у відправлене передавачем, з якого потім відкиданням контрольних розрядів відновлює початкове повідомлення.
Досконалий код Хеммінга
також можна будувати за розглянутою
схемою, оскільки для нього
 .
.
Для виправлення
одинарної помилки до 8-розрядного коду
досить приписати 4 розряди
 ,
до 16-розрядного - 5, до 32-розрядного - 6,
до 64-розрядного - 7.
,
до 16-розрядного - 5, до 32-розрядного - 6,
до 64-розрядного - 7.
Висновки
Передача інформації по каналах зв'язку найчастіше пов'язана з рішенням задачі перешкодостійкого кодування. При цьому групове кодування є одним з можливих варіантів рішення даної задачі.
Коди, що виявляють помилку, і коди, що коректують, обов'язково мають додаткові символи (надмірні).
Матричне кодування є одним з економних способів опису схеми кодування.
Груповий код – це блоковий код, у якого кодові слова утворюють групу.
Одними з найбільш поширених перешкодостійких кодів є коди Хеммінга.
У реальних системах для кодування інформації застосовується квазідосконале кодування.
Література
Чисар И., Кернер Я. Теория информации. М.: Мир, 1985
Блейхер Р. Теория и практика кодов, контролирующих ошибки. М.: Мир, 1986
Питерсон Р., Уэлдон Э. Коды, исправляющие ошибки. М.: Мир, 1976