Дистанційна слідкуюча система на сельсинах

Міністерство освіти і науки України

Житомирський державний технологічний університет

Кафедра А і КТ

Група АТ-12

Теорія автоматичного керування

Курсовий проект

„Дистанційна слідкуюча система на сельсинах”

Варіант №1

Схема №1

Виконав К.Г. Біденко

Перевірив С.С. Свістельник

Житомир 2006

Зміст

1. Завдання на курсовий проект

2. Опис роботи САК

3. Аналіз і синтез лінійної неперервної САК

3.1 Структурна схема САК

3.2 Визначення передаточної функції розімкнутої та замкнутої САК відносно вхідної

3.3 Визначення стійкості системи по критерію Гурвіца

3.4 Побудова амплітудно-фазової частотної характеристики (АФЧХ) та визначення стійкості САК за критерієм Найквіста. Дослідження системи методом D – розбиття

3.5 Побудова логарифмічної частотної характеристики САК та визначення запасів стійкості

3.6 Використовуючи логарифмічні частотні характеристики, виконання корекції САК в області середніх частот з метою отримання заданих запасів стійкості по фазі та амплітуді

3.7 Схема корегуючого пристрою та розрахунок його елементів

3.8 Розрахунок та побудова графіку перехідної характеристики скорегованої САК

3.9 Для заданого типу вхідної дії розрахунок та побудова графіку усталеної помилки скорегованої САК

3.10 Оцінка якості скорегованої САК

3.11 Моделювання системи в програмному модулі Simulink

4. Аналіз дискретної САК (ДСАК)

4.1 Визначення періоду дискретизації імпульсного елемента

4.2 Визначення передаточної функції розімкнутої та замкнутої ДСАК відносно вхідної дії

4.3 Визначення стійкості отриманої системи по критерію Гурвіца

4.4 Побудова логарифмічної псевдочастотної характеристики ДСАК та визначення запасів стійкості

4.5 Розрахунок та побудова графіку перехідної характеристики ДСАК

4.6 Для заданого типу вхідної дії розрахунок та побудова графіку усталеної помилки ДСАК.

4.7 Оцінка якості ДСАК

Висновки по роботі

Список літератури

Завдання на курсовий проект

Система керування описується наступними рівняннями:

СД - сельсин-датчик ,

СТ - сельсин-трансформатор де _>1>, _>0> - кут повороту вісі СД та СТ відповідно.

ИР - вимірювач неузгодженості

де U_>с> - напруга змінного струму

УН - підсилювач напруги та демодулятор

де U_>1> - напруга постійного струму

КУ - послідовний коригувальний пристрій схему коригувального пристрою розробити самостійно в ході проведення розрахунків (U_>2> - напруга постійного струму)

УМ - підсилювач потужності та

модулятор де U_>U>_>>- напруга змінного струму

ИД - виконавчий двигун

де - кут повороту валу виконавчого двигуна

ОУ - обмотка управління ИД

U_>U> - напруга управління змінного струму

ОВ - обмотка збудження ИД

U_>В> - напруга збудження змінного струму

Р - понижуючий редуктор

2. Опис роботи САК

Сельсин - електрична машина, що дозволяє здійснювати кутове переміщення вала якого-небудь пристрою або механізму відповідно до кутового переміщення іншого вала, механічно не пов'язаного з першим. За принципом дії сельсин являє собою поворотний трансформатор, у якого при обертанні ротора відбувається плавна зміна взаємної індуктивності між його обмотками - однофазною первинної (обмоткою збудження) і трифазною вторинної (обмоткою синхронізації). Залежно від виконуваних функцій (у системах "передачі кута") розрізняють сельсин - датчики (СД), сельсин - приймачі (СП) і диференціальні сельсин. Ротор СД механічно зв'язується з валом, що повертає, а в СП, електрично пов'язаного зі СД, поворот ротора синхронно й синфазно повторює поворот ротора СД. За допомогою диференціального сельсин алгебраїчно підсумують кутові переміщення двох механічно не зв'язаних між собою валів.

В одному з найпростіших випадків як СД, так і СП має однофазну обмотку, розташовану на роторі, і трифазну обмотку, з'єднану зіркою і розташовану в пазах статора. Однофазні обмотки підключаються паралельно до загальної мережі змінного струму, а трифазні з'єднуються один з одним. Якщо ротори СД і СП займають такі положення, при яких у їхніх обмотках синхронізації виникають рівні по величині, але протилежно спрямовані ЕРС, струм у ланцюзі синхронізації відсутній і ніякі обертаючі моменти, що діють на ротори, немає. При повороті ротора СД у ланцюзі синхронізації виникають відмінні від нуля сумарна ЕРС і струм. За рахунок взаємодії магнітних потоків обмоток збудження зі струмом в обмотках синхронізації в кожній з машин виникають обертаючі моменти; у СП цей момент прагне повернути ротор на кут, дорівнює куту повороту ротора СД, тобто перевести ротор у таке положення, при якому ЕРС, що наводять в обмотках синхронізації, знову вирівнюються.

Сельсини підрозділяють на контактні й безконтактні. У контактні сельсини одна з обмоток розташована на роторі, у зв'язку із чим останній має контактні кільця для з'єднання з іншими обмотками. У безконтактні С. обидві обмотки розташовані на статорі, причому вісь обмотки збудження перпендикулярна осі обмотки синхронізації; для зв'язку потоку порушення з обмоткою синхронізації використають рухливий магнітопровод (ротор) спеціальної форми, що дає можливість змінювати напрямок магнітного потоку в межах 90°.

Сельсини застосовують для контролю й керування в системах, що стежать, і для дистанційної передачі показань вимірювальних приладів.

Слідкуюча система, система автоматичного регулювання (керування), що відтворює на виході з певною точністю вхідний вплив, що задає, що змінюється по заздалегідь невідомому закону. Слідкуюча система може мати будь-яку фізичну природу й різні способи технічного здійснення. Блок-схема пояснює загальний принцип дії слідкуючої системи. Один з основних елементів слідкуюча система - пристрій, що порівнює, у якому виробляється порівняння вихідної величини, що фактично виходить, х із заданою вхідною величиною g(t) і виробляється сигнал неузгодженості  = g(t)-x. Передача величини х з виходу на вхід здійснюється по ланцюзі негативного зворотного зв'язку; при цьому знак х міняється на зворотний. Так як, за завданням повинне бути х = g(t), та неузгодженість є помилкою слідкуючої системи. Ця помилка в добре працюючій слідкуючій системі повинна бути досить малою. Тому сигнал е підсилюється й перетвориться в новий сигнал u, що пускає в хід виконавчий пристрій. Виконавчий пристрій змінює х так, щоб ліквідувати неузгодженість. Однак через наявність різних впливів, що обурюють, f(t) і перешкод n(t) неузгодженість виникає знову, і слідкуюча система увесь час працює на його знищення, тобто "стежить" за ним й, у підсумку, за заданою величиною g(t). Для здійснення процесу керування з необхідною точністю застосовують спеціальні коригувальні пристрої, що входять до складу підсилювача-перетворювача, і додаткові місцеві зворотні зв'язки. У результаті сигнал і досить складним образом залежить від їй від параметрів стану самого виконавчого пристрою. У деяких випадках слідкуючої системи відтворюють вхідну величину g (t) в іншому масштабі x(t)=kg(t), де k - масштабний коефіцієнт, або відповідно до більше складного функціонального зв'язку x (t)= = F [g (t)].

Приклад слідкуючої системи - система відпрацьовування на вихідному валу кута повороту, що задає довільно на вході, 1(t).

Неузгодженість  = 1(t) - 2 виробляється з'єднаними за трансформаторною схемою сельсинами - датчиком і приймачем (останній пов'язаний з вихідним валом). Виконавчим пристроєм є система "генератор-двигун" з редуктором; вплив, що обурює, - зміна навантаження на вихідному валу.

За принципом слідкуючої системи працюють системи наведення. У слідкуючих системах антени радіолокаційної станції неузгодженістю служить кутова помилка між радіолокаційним променем і напрямком на мету; виконавчий пристрій - електропривод антени. Автопілот наводить ракети, що, також працює за принципом слідкуюча система, причому для нього неузгодженістю служить відхилення ракети від напрямку променя, а виконавчим пристроєм є кермова машинка й рулі. За принципом слідкуючої системи працюють багато систем телекерування й самонаведення. Слідкуючою системою є також вимірювальні прилади, що працюють по компенсаційному принципі; у них неузгодженістю служить різниця між показанням приладу й вхідною вимірюваною величиною. За принципом слідкуючої системи працюють деякі обчислювальні пристрої. Слідкуючої системи, вихідною величиною яких є механічне переміщення, називається приводом, що стежить. Приклади слідкуючої системи можна виявити й у живих організмах.

Розрахунок слідкуючої системи при її проектуванні в цілому заснований на теорії автоматичного регулювання й керування. Слідкуючі системи можуть мати безперервне керування (лінійне, нелінійне) або дискретне (релейне, імпульсне, цифрове), що відбивається на виборі методу динамічного розрахунку. Крім того, виробляється технічний розрахунок кожного блоку й елемента. Одна з головних цілей динамічного розрахунку слідкуючої системи - синтез коригувальних пристроїв виходячи із заданих вимог до якості процесу керування.

3. Аналіз і синтез лінійної неперервної САК

3.1 Структурна схема САК

Рис. 1. Структурна схема досліджуваної САК в загальному випадку

Для варіанту №1 САК матиме наступний вигляд (рис. 2):

Рис. 2. Структурна схема вказаної САК згідно з варіантом

Визначимо передатні функції розімкненої та замкненої САК відносно вхідної

а) передатну функцію розімкненої САК визначимо як добуток передатних функцій усіх ланцюгів САК, оскільки маємо послідовне з’єднання ланцюгів. Таким чином

w(s)=w_>ир>(s)·w_>ун>(s)·w_>ум>(s)·w_>ид>(s)·w_>р>(s) =,

w(s) = .

Схема розімкненої САК зображена на рис. 3.

б) передатну функцію замкненої САК отримаємо за формулою

Ф(s) = :

Ф(s) = .

Зображення схеми замкненої САК зображена на рис. 4.

3.3 Визначимо стійкість системи по критерію Гурвіца

Знаючи перехідну функцію, знайдемо характеристичне рівняння системи:

D(s)=.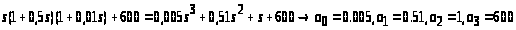

На основі отриманих коефіцієнтів характеристичного рівняння побудуємо головний визначник Гурвіца:

 = .

За критерієм Гурвіца для того, щоб система автоматичного керування була стійкою, необхідно та достатньо, щоб при а_>0>>0 всі визначники Гурвіца були додатними. Умовою стійкості для системи третього порядку будуть: а_>1>·a_>2>>a_>0>·a_>3>.

В даному випадку: а_>0>= 0,005 > 0; а_>1>·a_>2>= 0,51·1 = 0,51; a_>0>·a_>3>= 0,005·600 = 3; 0,51<3. Умова стійкості системи не виконуються, отже за критерієм Гурвіца САК нестійка.

а). Побудуємо амплітудно-частотну характеристику в визначимо стійкість системи по критерію Найквіста:

1) запишемо перехідну характеристику розімкнутої САК

w(s)=.

2) в рівнянні перехідної функції проведемо заміну s→j·ω та проведемо всі можливі перетворення та спрощення, тоді

w(j·ω) = =

= = .

Дійсна частина цього виразу

Re(w(j·ω)) = = Х(ω),

уявна частина – Im(w(j·ω)) = = У(ω).

3) Побудуємо на комплексній площині (Х0У) криву Найквіста та зробимо висновок про стійкість системи:

У(ω) = 0 → ω = 0 → Х(0) = 0;

У(ω) = 0 → ω = =14 →

Х(14) = = -6.

По цим точкам побудуємо криву Найквіста (рис. 5).

Критерій Найквіста: Для того щоб замкнута система була стійкою необхідно, щоб годограф розімкненої системи починаючись на дійсній вісі і рухаючись проти годинникової стрілки (при змінній частоті від 0 до ∞) не охоплював точку (-1, j0).

Замкнена САК охоплює точку (-1, j0), що видно на рис. 5. Отже, САК нестійка.

б). Дослідження системи методом D – розбиття

За даними, що були отримані в пункті 3.3 знайдемо критичний коефіцієнт підсилення системи k_>кр>:

0,51 ≥ k·0,005

k ≤ 102

k = 102 (теоретично розрахований коефіцієнт підсилення).

Використовуючи методику D-розбиття та за допомогою програми MathCad побудуємо межу D-розбиття, обравши за параметр дослідження коефіцієнт підсилення системи.

Характеристичний поліном САК, враховуючи, що параметр, який досліджується, коефіцієнт підсилення:

D(p) = .

Звідси k(p) = і k(ωj) =

Побудуємо область D-розбиття, знаючи, що Re(k) = , Im(k) = = (див. рис. 6).

На побудованій області D- розбиття можна визначити коефіцієнт підсилення (точка перетину області з дійсною віссю).

3.5 Побудова логарифмічної частотної характеристики САК та визначення запасів стійкості

Знаючи перехідну характеристику розімкненої САК

w(s)=,

знайдемо нульову контрольну точку: L_>0> = 20lgk = 20lg600 = 55,6 дБ.

2) Визначимо спряжені частоти: ω_>1> = 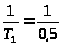= 2с^-1; ω_>2> = = 100с^-1.

3) Враховуючи, що до складу системи входить пропорційна, інтегруюча та дві аперіодичні ланки першого порядку ЛАХ і ЛФХ для даної САК (рис. 7).

Як видно з графіків, оскільки ЛАХ перетинає вісь 0ω під нахилом -40, а ЛФХ перетинає пряму –π, система є нестійкою.

Знайдемо запаси стійкості системи за ЛАХ та ЛФХ:

 по амплітуді: ΔL = 20lg (w(j*ω_>с>)), де ω_>с> – частота, за якої φ(ω_>c>) = -π. З графіка видна ω_>c> = 25 (див. рис.7). Тоді ΔL = 20lg (w(j*ω_>с>)) = 20lg (w(j*25)) = -16.

Порівнюємо з значенням визначеним критерієм Найквіста h=20lg(1/Wcp) = =20lg(1/6)= 15,6 з h=16 знайденому по рис. 7.

 по фазі: Δφ = π-Arg(w(j*ω_>з>)), де ω_>з> – частота зрізу, коли L(ω_>з>) = 1, тобто

ω_>з> = 34. Тоді Δφ = arg(w(j*34)) = -40°.

Корекцію системи проведемо при заданих якісних параметрах (час регулювання t_>p> = 0,3с перерегулювання δ = 30%). Побудуємо ЛАХ бажаної роботи системи та корегуючого пристрою (рис. 8).

Складемо передаточні характеристики для бажаної та корегуючої систем:

w_>б>(s) = Враховуючи, що w_>б>(s) = w_>з>(s)·w_>к>(s),

отримаємо

w_>к>(s) = .

3.7 Схема корегуючого пристрою та розрахунок його елементів

Приведемо схему корегуючого пристрою, обравши його з довідника. Згідно з наявною ЛАХ, що приведена вище, найбільше нашим вимогам задовольняють схеми №52 та №33 корегуючого пристрою (рис. 9).

в) г)

Рис. 9. Схеми корегуючого пристрою та відповідні фрагменти ЛАХ: а) фрагмент ЛАХ, що відповідає схемі №52; б) фрагмент ЛАХ, що відповідає схемі №33; в) схема №52 (К1) , г)схема №33 (К2).

Розрахуємо кожен з елементів схем:

Для схеми №52

L_>0>=,L_>>=.

Оберемо ємності конденсаторів: С1=100мкФ, С2=100мкФ.

Т_>1> = .

3) T_>2>_>>= 

Оберемо підсилювач з таким коефіцієнтом:

20lgk=-22,5, k=10^(-22,5/20)=0,075 (П1).

Підберемо з ряду опорів Е24 відповідні значення опорів:

R1 = 24 кОм, R2 = 27 кОм.

Для схеми №33

L_>0>=,L_>>=.

Оберемо ємності конденсаторів: С1=100мкФ, С2=100мкФ та значення опору R2=1кОм.

Т_>1> = .

T_>2>_>>= .

Оберемо підсилювач з таким коефіцієнтом підсилення: 20lgk=22,5, k=10^(22,5/20)=13,34 (П2).

Підберемо з ряду опорів Е24 відповідні значення опорів: R1 = 0,03кОм, R2 = 1 кОм, R3 = 0,1кОм, R4 = 1 кОм.

Загальна схема корегуючого пристрою має такий вигляд:

3.8 Розрахунок та побудова графіку перехідної характеристики скорегованої САК

Визначимо аналітичний вираз для перехідної характеристики замкнутої скоректованої системи за передаточною функцією розімкнутої САК при одиничному ступінчатому вхідному сигналі та побудуємо графік.

Передатна функція w(s) = .

Передатна функція замкненої системи:

Перехідна характеристика замкненої системи за вхідним сигналом: H(s)=G(s)*Ф(s), де G(s) = - одиничний ступінчатий вхідний сигнал.

H(s) = .

Графік перехідної характеристики САК зображений на рис. 10.

Рис. 10. Перехідна характеристика САКк

3.9 Для заданого типу вхідної дії розрахунок та побудова графіку усталеної помилки скорегованої САК

Дослідимо точність замкнутої системи за передаточною функцією розімкнутої САК. При дослідженні визначимо три коефіцієнти помилок С0, С1, С2, використовуючи передаточну функцію замкнутої системи за похибкою:

Ф_>x>(s) =

Тоді

Тобто С0 = 0, С1 = 0,0017, С2 = 0,008.

Побудуємо графіки помилок в усталеному режимі при:

- одиничному ступінчатому сигналі G1(t) = 1 (G1(s) = 1/s) (рис. 11).

- помилка від вхідної керуючої дії.

- усталена похибка.

при сигналі G2(t) = 20+40t+5t² (рис. 12),

- помилка від вхідної керуючої дії.

- усталена похибка.

3.10 Оцінка якості скорегованої САК

Оцінимо якість перехідних процесів у заданій системі:

- перерегулювання δ – відносне максимальне відхилення перехідної характеристики від усталеного значення вихідної координати, виражене у відсотках: δ = . (h_>max>, h_>уст> – відповідно максимальне та усталене значення перехідної характеристики для досліджуваної системи побачимо на графіку (рис.10))

δ = .

- час регулювання (час перехідного процесу) t_>p> – мінімальний час, після сплину якого регульована координата буде залишатися близькою до усталеного значення із заданою точністю .

, тоді t_>p> = 0,47 (с).

- число коливань n, яке має перехідна характеристика h(t) за час регулювання t_>p>: n = 1.

Висновок: приведені вище розрахунки та дослідження показують, що задана система є нестійкою, але її можна скорегувати порівняно нескладними корегуючими пристроями (передаточна функція після корегування має пропорційну, інтегруючу, форсуючу та три аперіодичні ланки першого порядку), метод розрахунку яких приведений вище; при роботі системи спостерігали усталену похибку САК з заданою вхідною дією, розрахунок провели за допомогою приведених вище формул.

3.11 Моделювання системи в програмному модулі Simulink

Змоделюємо систему в програмному модулі Simulink – зберемо структурну схему отриманої скоректованої системи (рис. 13).

Рис. 13. Модель скоректованої САК в програмному модулі Simulink

Реакція системи на одиничний ступінчатий сигнал (рис. 14).

Порівнюючи реакцію САК, отриману за допомогою моделювання (рис. 14), з теоретично отриманою перехідною характеристикою (рис. 10) в пункті 3.8 виявили, що вони співпали (розрахунки в обох випадках проведені правильно).

Побудова графіка вихідної координати при заданій вхідній дії

g(t) = 20+40t+5t² (рис. 16).

Змоделюємо систему з заданою вхідною дією в програмному модулі Simulink (рис. 15).

Рис. 15. Модель САК з заданою вхідною дією

Реакція системи на вхідний сигнал (рис. 16).

Рис. 16. Реакція САК на задану вхідну дію

З графіків видно, що робота системи залежить від вхідного сигналу.

4. Аналіз дискретної САК (ДСАК)

В основі аналізу дискретної САК візьмемо лінійну неперервну САК після корекції з передаточною характеристикою

w(s) = .

4.1 Визначення періоду дискретизації імпульсного елемента

В якості формоутворювача сигналу приймемо екстраполятор нульового порядку.

ω_>з>= 125с^-1 – максимальна частота в спектрі вхідного сигналу.

За теоремою Котельникова для нормальної роботи системи необхідно, щоб виконувалася умова T_>k> = - період дискретизації, відповідно ω_>к>≥ 2ω_>з> – частота дискретизації. Оберемо ω_>к>≥ 3·125 = 375 с^-1, тоді T_>k>≤ (с).

Виберемо період дискретизації T_>k> = 0,006с, ω_>к> = 628 с^-1.

4.2 Визначення передаточної функції розімкнутої та замкнутої ДСАК відносно вхідної дії

w(z) = .

Спочатку розкладемо функцію на простіші дроби:

Виконаємо z-перетворення Лапласа отриманої функції:

Отже,

Передатна функція замкненої ДСАК:

4.3 Визначення стійкості отриманої системи по критерію Гурвіца

Знаючи перехідну функцію, знайдемо характеристичне рівняння системи: D(s)=.

Виконаємо білінійне перетворення .

Отримаємо наступне характеристичне рівняння:

На основі отриманих коефіцієнтів характеристичного рівняння побудуємо головний визначник Гурвіца:

 = .

За критерієм Гурвіца для того, щоб система автоматичного керування була стійкою, необхідно та достатньо, щоб при а_>0>>0 всі визначники Гурвіца були додатними.

а_>0>=7,50340,

Умова стійкості системи виконуються, отже за критерієм Гурвіца САК стійка.

4.4 Побудова логарифмічної псевдочастотної характеристики ДСАК та визначення запасів стійкості

Для побудови логарифмічної псевдочастотної характеристики використаємо передаточну функцію розімкненої системи після корекції та виконання z- перетворення:

Виконаємо , де  - абсолютна псевдочастота, с^-1.

Знайдемо нульову контрольну точку: L_>0> = 20lgk = 20lg599,98 = 55,6 дБ.

Визначимо спряжені частоти:

λ_>1> = = 256с^-1, λ_>2> = = 154с^-1,

λ_>3> = = 0,4с^-1, λ_>4> = = 312,5с^-1, λ_>5> = = 11с^-1,

λ_>6> = = 322,6с^-1.

Враховуючи, що до складу системи входить пропорційна, інтегруюча, три аперіодичні ланки першого порядку та три форсуючі ланки отримуємо ЛАХ і ЛФХ для даної САК (рис. 17).

Рис. 17. Логарифмічні частотні характеристики системи.

Знайдемо запаси стійкості системи за ЛАХ та ЛФХ:

 по амплітуді запас стійкості h= (L), тому що ЛФХ не перетинає межу -.

 по фазі: Δφ = π-Arg(w(j*ω_>з>)), де ω_>з> – частота зрізу, коли L(ω_>з>) = 1, тобто

ω_>з> = 8. Тоді Δφ = arg(w(j*8) = -38°.

4.5 Розрахунок та побудова графіку перехідної характеристики ДСАК

Для побудови перехідної характеристики ДСАК використаємо перехідну характеристику замкненої системи отриману раніше.

Розрахуємо перехідну характеристику ДЦСАК Y(z) = Ф(z)*G(z), де G(z) = - зображення вхідного одиничного сигналу. Тобто

Побудуємо графік перехідного процесу, попередньо розклавши перехідні характеристики в ряд Лорана:

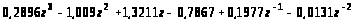
Тобто С_>0>=0,1677, C_>1> = 0,1822, C_>2> = 0,241, C_>3> = 0,327, C_>4> = 0,4237, C_>5> = 0,522. За цими даними побудуємо графік - гістограму перехідного процесу (рис. 18).

Рис. 18. Перехідна характеристика досліджуваної ДСАК

Провівши розрахунки та побудову за допомогою Math Lab отримали такі результати:

Отримані перехідні характеристики в обох випадках не співпадають, що означає неточність розрахунків, а також специфіка розрахунку передаточних відношень в Math Lab.

4.6 Для заданого типу вхідної дії розрахунок та побудова графіку усталеної помилки ДСАК

Ф_>x>(z) = .

Виконаємо заміну, тоді отримаємо такий вираз:

Для побудови графіку усталеної похибки визначимо коефіцієнти С_>0>та С_>1>– коефіцієнти похибок, які є коефіцієнтами розкладу передаточної функції системи за похибкою Ф_>x>(z) в ряд Маклорена за степенями s, тобто

, в нашому випадку:

В загальному випадку при вхідній дії, що повільно змінюється, усталену похибку системи можна представити у вигляді ряду

В нашому випадку при g(n)=20+40n+5n² усталена похибка має вигляд:

Рис. 19. Графік усталеної похибки ДСАК.

4.7 Оцінка якості ДСАК

Для оцінки якості ДСАК розрахуємо та побудуємо перехідну характеристику.

Рис. 20. Перехідна характеристика ДСАК

Оцінимо якість перехідних процесів у заданій системі:

δ = .

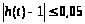, тоді t_>p> = 58 (с).

- число коливань n, яке має перехідна характеристика h(t) за час регулювання t_>p>:n = 1.

Висновок: провівши аналіз ДСАК можна сказати, що отримана система після квантування є стійкою, коефіцієнт підсилення співпадає з коефіцієнтом підсилення лінійної САК; отримані результати вказують на те, що аналіз проведений правильно, хоча деякі якісні параметри ДСАК відрізняються від лінійної САК, це вказує на те, що деяка інформація про систему під час квантування все ж втратилась.

Висновок

При дослідженні та аналізі дистанційної слідкуючої системи на сельсинах за критеріями Гурвіца, Найквіста та частотними критеріями система виявилася не стійкою, а за допомогою D – розбиття було досліджено, що для даної системи достатньо коефіцієнта підсилення 102 замість 600. Виконали корекцію методом синтезу послідовних корегуючих пристроїв розблених проф. Солодовніковим. Таким чином було введено два корегуючих пристрої та знайдена бажана передаточна функція. Подальші дослідження проводилися за бажаною передатною функцією. Так оцінили якість скорегованої САК за такими параметрами: перерегулювання 27,27%, час перехідного процесу 0,47с та число коливань n=1. Отримані параметри є допустимими, тому можна вважати, що робота скорегованої системи проходить якісно та точно.

Моделювання системи в програмному модулі Simulink дозволило показати графічно як на систему впливають різні вхідні сигнали та ще раз підтвердити точність проходження скорегованої САК.

Аналізуючи дискретну САК провели дослідження за критерієм Гурвіца та частотними критеріями, щоб потім порівняти результати з результатами лінійної САК. ДСАК дещо відрізняється від лінійної САК, що означає втрату деяких параметрів лінійної САК після її квантування. Хоча в цілому ДСАК за всіма досліджуваними критеріями є стійкою, а якість та точність перехідного процесу задовольняє допустимим параметрам.

Список літератури

Самотокін Б.Б. Лекції з теорії автоматичного керування. –Житомир ЖІТІ, 2001. -504с.

Топчеев Ю.А. Атлас для проектирования систем автоматического регулирования. –Москва „Машиностроение”, 1989. -752с.

Свечарник Д.В., Дистанционные передачи, 3 изд., М. — Л., 1974.

Кочетков В.Т., Половко А.М., Пономарев В.М., Проектирование и расчет следящих систем, Л., 1964;

Бесекерский В.А., Попов Е.П., Теория систем автоматического регулирования, 3 изд., М., 1975.