Основные характеристики пространственной структуры излучения
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
кафедра ЭТТ
РЕФЕРАТ на тему:
«Основные характеристики пространственной структуры излучения»
МИНСК, 2008
До сих пор при
изложении вопросов обнаружения сигналов
на фоне помех учитывалась только
их временная
структура. В то же время как сигналы,
так и помехи являются электромагнитными
полями, которые характеризуются
амплитудными
и фазовыми
распределениями
на раскрыве передающей или приемной
антенны, где x,y
- координаты раскрыва.
Под пространством
сигнала будем понимать для определенности
плоскость (x,y).
На плоскости (x,y)
в пределах площади
существует
поле f(x,y,t),
а внеполе
равно нулю (рис. 2.9.1)
где A(x,y,t)
и
-
амплитуда и фаза поля.
Пусть пространственный сигнал f(x,y) представляет распределение на плоскости Z = 0, т.е. на плоскости (x,y), амплитуд и фаз поля монохроматического колебания
,
где
-
амплитуда, круговая частота и начальная
фаза монохроматического колебания.
При этом поле в полусфере бесконечного радиуса при Z > 0, опирающейся на плоскости Z = 0, является суммой плоских волн с различными амплитудами, фазами и направлениями распространения:
Рис. 1. Пространство сигнала.
Рис. 2. Проекции волнового вектора на координатные оси.
где
- радиус-вектор, проведенный из начала
координат в точку наблюдения;
- волновой вектор, модуль которого
;
- проекция волнового вектора;
- комплексная функция, которая
описывает амплитуду и фазу отдельной
плоской волны с направлением
распространения, определяемым
совокупностью двух действительных
переменных
и
.
Заметим, что факт распространения плоской волны в любом направлении отражается условием сохранения фазы волнового фронта, распространяющегося со скоростью света С :
,
если
.
Факт суммирования плоских волн, распространяющихся во всех направлениях передней полусферы, отражается их двойным интегрированием по всем направлениям.
Направление
распространения волна определяется
проекциями волнового вектора на
координатные оси (рис.2). В общем случае
направление распространения волны
определяется двумя
углами
и
.
Если эти углы выбраны по отношению к
прямоугольной системе координат x,
y,
z
так, как показано на рис. 2, то
,
.
Так как три проекции
волнового вектора связаны соотношением
,
то независимых проекций всего две -
и
,
а третья проекция
.
Используя введенные обозначения, перепишем выражение для искомого поля так
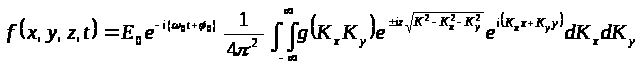Определим
комплексную функцию
.
Очевидно, что приведенное решение
волнового уравнения должно удовлетворять
следующему условию – на плоскости Z=0
это решение должно иметь вид заданного
пространственного сигнала
Полученное выражение
представляет собой обратное двумерное
преобразование Фурье. Прямое двумерное
преобразование Фурье позволяет найти
функцию
:
.
Функция
,
определяющая распределение амплитуд
и фаз плоских волн по направлениям
согласно последнему выражению может
быть названа спектром волнового поля
или угловым спектром поля. Название
“угловой спектр” отражает связь
аргументов
и
с углами распространения
и
соответствующих плоских волн.
Последние два
соотношения представляют собой прямое
и обратное преобразование Фурье для
двух переменных -
и
(x,
y).
Переменные x,
y
являются координатами точек пространства
и имеют размерность длины. Переменные
и
имеют размерность, обратную длине. Эти
переменные называются пространственными
частотами. Такое название вполне
оправдано. Параметр x
или у в пространственном сигнале подобен
времени t
во временном сигнале, а параметр
или
подобен
круговой частоте в спектре временного
сигнала. Поэтому оправданным является
и другое обозначение переменных
и
как круговых пространственных частот
,
.
Таким образом,
переменные
и
имеют двойной физический смысл – это,
с одной стороны, пространственные
частоты, а с другой стороны, величины,
определяющие углы распространения
плоских волн, на которые разлагается
волновое поле.
Решение волнового уравнения остается двузначным, так как можно выбрать любой из двух знаков перед координатой z в показателе экспоненты. Эта неопределенность знака устраняется, если учесть поведение неоднородных волн при увеличении z.
В отличие от распространяющихся плоских волн при
неоднородные волны получаются при
,
которые экспоненциально затухают вдоль координаты z. При этом убывающее с ростом z поле мы получим только в том случае, если выберем в указанном показателе экспоненты перед z знак ''+". С учетом этого решение волнового уравнения, определяющее комплексную амплитуду поля в передней полусфере в виде суперпозиции плоских волн различных направлений (в том числе и неоднородных) с различными амплитудами и фазами, обретает окончательный вид
Заметим, что решение волнового уравнения является отражением двух базовых явлений: явления дифракции радиоволн, т.е. отклонения направления распространения радиоволн от нормали к излучающему раскрыву, и явления интерференции радиоволн, т.е. сложения (суперпозиции) плоских радиоволн с различными амплитудами, фазами и направлениями распространения.
Сомножитель
подынтегральном выражении доопределяет
фазу каждой составляющей углового
спектра поля с учетом того, что сигнал
в передней полусфере наблюдается на
плоскости, перпендикулярной оси z
на расстоянии z
от плоскости
входного пространственного сигнала.
Поэтому этот сомножитель условно может
рассматриваться как частотная
характеристика свободного пространства
.
Амплитудно-частотная характеристика свободного пространства для распространяющихся в передней полусфере радиоволн равна единице
,
,
,
где
- координаты волнового вектора в полярной
системе координат (рис. 2.9.2):
,
,
- угол между направлением
распространения плоской радиоволны и
осью z,
т.е. угол отклонения (дифракции)
электромагнитных волн от направления,
перпендикулярного плоскости
пространственного сигнала.
Фазочастотная характеристика свободного пространства
изображена на рис. 3.
Поведение фазочастотной
характеристики свободного пространства
представляет наибольший интерес в
диапазоне пространственных частот,
равной ширине амплитудно-частотного
спектра пространственного сигнала,
которая по аналогии с шириной спектра
временного сигнала
определяется пространством сигнала :
,
,
,
где
- обобщенный линейный размер пространства
сигнала.
Это означает, что поведение фазочастотной характеристики свободного пространства представляет интерес в диапазоне углов дифракции:
.
Учитывая это, фазочастотная характеристика свободного пространства может приближенно рассматриваться в различных условиях дифракции:
1) в условиях
приближения геометрической оптики
изменением ФЧХ свободного пространства
в диапазоне углов дифракции
можно пренебречь
Рис. 3. Фазочастотная характеристика свободного пространства.
Рис. 4. Диаграмма направленности антенны при равномерном АФР.
,
если
второе (отброшенное) слагаемое разложения
в ряд Маклорена много меньше
радиан
,
что выполняется в области глубокой ближней зоны
.
2)
в условиях дифракции Френеля фазочастотную
характеристику свободного пространства
в диапазоне углов дифракции
можно аппроксимировать параболой
,
если
третье (отброшенное) слагаемое разложения
в ряд Маклорена много меньше
радиан
,
что выполняется на расстояниях
т.е. практически в области ближней зоны
.
3)
в условиях дифракции Фраунгофера, когда
изменение фазочастотной характеристики
свободного пространства в диапазоне
углов рефракции
больше
радиан
т.е. практически в области дальней зоны
.
При этом решение дифракционной задачи упрощается в большей мере, чем даже в частных случаях дифракции Френеля или приближения геометрической оптики. Действительно, поле в дальней зоне, используя полярную систему координат
,
,
,
можно представить в следующем виде:
.
Учитывая ограниченную
область изменения пространственной
частоты
,
относительно малые размеры пространства
сигнала
,
относительно небольшой диапазон
изменения углов дифракции
,
можно вычислить интеграл путем ряда
уточнений, преобразований переменной
интегрирования упрощений:
- уточнение пределов интегрирования
,
- упрощение подынтегрального выражения
,
,
-
переход к переменной интегрирования
,
а от нее – к переменной
Дальнейшее
вычисление интеграла основано на
использовании относительно медленного
изменения функции
по
сравнению с изменением функций
и
в дальней зоне
.
Это позволяет вынести за знак интеграла
функцию
:
.
Осуществляя замену переменной интегрирования
,
приводим выражение в интегралах Френеля
.
Учитывая асимптотические свойства интегралов Френеля,
,
находим окончательно:
.
Возвращаясь
к двумерному интегралу, определяющему
поле в дальней зоне источника излучения
(в плоскости
),
с точностью до несущественного постоянного
фазового сдвига, получаем
.
Таким образом, в дальней зоне (зоне Фраунгофера) распределение поля определяется формой спектра исходного поля. Этот результат широко известен в теории антенн, где распределение поля по углам в дальней зоне (диаграмма направленности антенны) есть преобразование Фурье от распределения в раскрыве антенны.
При регулярном АФР поля в плоскости излучения диаграмма направленности характеризуется наличием главного лепестка определенной формы и ширины,а также наличием боковых лепестков определенного уровня. Так, например, при равномерном распределении (АФР) поля на раскрыве
,
,
,
диаграмма
направленности излучения имеет форму
в обеих плоскостях:
Угловая ширина диаграммы направленности антенны пропорциональна ширине спектра пространственного сигнала
,
.
Таким образом, диаграмма направленности антенны и ее ширина (рис. 4) является важнейшими пространственными характеристиками излученного (зондирующего) сигнала, определяющими направленность излучения антенной системы с регулярным амплитудно-фазовым распределением поля на ее разрыве.
ЛИТЕРАТУРА
Охрименко А.Е. Основы извлечения, обработки и передачи информации. (В 6 частях). Минск, БГУИР, 2004.
Девятков Н.Д., Голант М.Б., Реброва Т.Б.. Радиоэлектроника и медицина. –Мн. – Радиоэлектроника, 2002.
Медицинская техника, М., Медицина 1996-2000 г.
Сиверс А.П. Проектирование радиоприемных устройств, М., Радио и связь, 2006.
Чердынцев В.В. Радиотехнические системы. – Мн.: Высшая школа, 2002.
Радиотехника и электроника. Межведоств. темат. научн. сборник. Вып. 22, Минск, БГУИР, 2004.