Оптимальність у системах керування

оптимальність у системах керування

1. Умови оптимальності у неавтономних системах керування

У загальному випадку неавтономної системи права частина закону руху й підінтегральна функція цільового функціонала залежать явно від часу , тобто закон руху має вигляд:

, (1)

а цільовий функціонал дорівнює

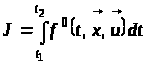. (2)

Тут функції і – неперервні по сукупності змінних і неперервно диференційовані по змінних , , .

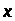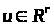Також вважатимемо, що момент часу 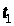, який відповідає початковому стану 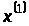, відомий, а момент часу проходження через кінцеву точку не заданий і повинен бути знайдений, тобто сформульована задача – це задача з вільним часом.

Поставлена задача може бути зведена до автономної задачі введенням додаткової змінної . До закону руху при цьому додається рівняння

,

а до початкових умов – співвідношення .

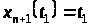Тепер систему (2) можна переписати у вигляді:

(3)

а функціонал дорівнюватиме

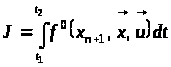, (4)

де 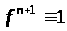(відповідно до доданого у початкову систему рівняння).

Отже, неавтономну -вимірну задачу було зведено до автономної задачі з розширеним фазовим простором. У новій задачі потрібно знайти оптимальну траєкторію, що поєднує точку розширеного фазового простору з деякою точкою на прямій, яка проходить через точку 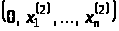паралельно осі . Оскільки кінцеве значення змінної 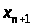невідоме, то нова задача – це задача з фіксованим лівим і рухомим правим кінцями.

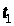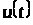Якщо в задачі оптимального керування (3) – (4) відомі і початковий момент часу й кінцевий момент часу , то задача називається задачею з фіксованим часом. Перетворення цієї задачі введенням додаткового змінного приводить до задачі з фіксованими кінцями в такому формулюванні. Потрібно знайти керування , що переводить фазову точку системи (2) зі стану в момент часу 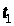у стан в момент часу , причому функціонал (4) набуває найменшого значення. Зауважимо, що момент часу попадання в точку можна не вважати фіксованим, оскільки в силу тотожності 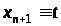попадання в точку може відбутися тільки в цей момент часу. Таким чином, до даної задачі можна застосувати теорему, відповідно до якої для одержання необхідних умов екстремуму функціонала необхідно максимізувати функцію Понтрягіна

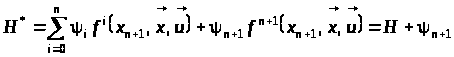, (5)

де – загальний вигляд функції Понтрягіна з теореми 1, у якій не врахована додаткова, (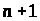)-ша змінна. Спряжена система для цієї задачі за умов 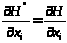набуває вигляду:

(6)

Має місце така теорема.

Припустимо, , – оптимальний процес для задачі з фіксованим часом. Тоді існує ненульова вектор-функція , що відповідає цьому процесу, така що:

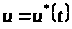1. Для будь-якого функція змінної набуває максимального значення в точці , тобто:

: .

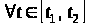2. , .

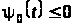Оскільки, як і раніше, 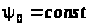, то умову 2 цієї теореми достатньо перевірити в якій-небудь одній точці відрізка .

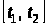Розглянемо випадок, коли при фіксованому правий кінець вільний. Ця задача полягає в тому, щоб із заданого стану 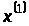за заданий час 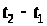пройти по траєкторії з довільним кінцевим станом за умови мінімізації цільового функціонала. Умови трансверсальності для цієї задачі набувають вигляду:

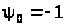, . (7)

Для цього випадку необхідна умова оптимальності полягає в тому, щоб функція досягала максимального значення для кожного на оптимальному керуванні 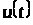і мала місце умова (7).

2 Поняття особливого керування

На практиці часто зустрічаються задачі оптимального керування, у яких функція Понтрягіна лінійно залежить від всіх керувань або від частини з них (наприклад, в лінійних задачах оптимальної швидкодії). Однак у нелінійних задачах оптимального керування (якщо функція Понтрягіна є нелінійною по одній або декількох фазових змінних) можлива ситуація, коли на оптимальній траєкторії коефіцієнт при одній з компонент вектора керування обертається на нуль всюди на деякому інтервалі часу, і тоді умова максимуму функції за не дозволяє однозначно визначити оптимальне керування. Ця ситуація називається особливим режимом керування. Дослідимо її детальніше.

Розглянемо автономну задачу оптимального керування

,

Де ; , , , ,

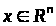– довільна множина з ;

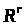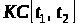– лінійний простір кусково-неперервних на функцій.

Крайові умови задачі мають вигляд:

, .

Потрібно знайти таке припустиме керування 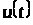, що переводить систему зі стану 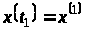у стан 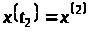, причому відповідний припустимий процес 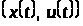доставляє мінімальне значення функціоналу

,

де функції , неперервні по сукупності всіх змінних і неперервно-диференційовані по змінних .

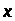Вважатимемо, що функція Понтрягіна для цієї задачі є лінійною за частиною компонент вектора 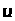. Виділимо із цих компонент групу з керувань (з тих, за якими функція лінійна) і позначимо їх через , а інші керувань зберемо у вектор 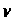(він також може включати компоненти, за якими функція лінійна). За таких умов закон руху набуває вигляду:

,

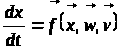де .

Складемо функцію Понтрягіна для даної задачі:

.

Очевидно, що

, . (8)

Припустимо, що процес разом з розв’язком спряженої системи

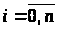, , (9)

задовольняє принципу максимуму і, крім того, припустимо, що у всіх точках деякого інтервалу має місце рівність

, (10)

або, враховуючи (10),

, , . (11)

Ця ситуація означає, що коефіцієнти при на деякому часовому відрізку дорівнюють 0, і оптимальне керування визначити неможливо. У цьому випадку вектор керувань називається особливим керуванням на відрізку 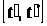, процес – особливим режимом, траєкторія – траєкторією особливого режиму, а відрізок часу 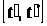– ділянкою особливого керування.

З формули (11) випливає, що на ділянці особливого режиму функція Понтрягіна не залежить від . Дійсно, :

.

Тому в даній ситуації умова максимуму по не дає жодної інформації про конкретні значення керувань .

Оскільки на ділянці особливого режиму має місце співвідношення (11), то очевидно, що

,

і т.д. Останні співвідношення разом з умовою (10) дозволяють визначити всі особливі режими.

3. Лінійна задача оптимальної швидкодії

Розглянемо лінійну задачу оптимальної швидкодії:

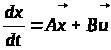, , (12)

де , ,

, – числові матриці розмірності та відповідно.

Область керування задачі – замкнутий обмежений багатогранник в :

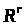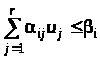, , (13)

Якщо для будь-якого вектора 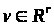, паралельного будь-якому ребру багатогранника , система векторів , , 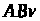…, (14) є лінійно незалежною, то багатогранник задовольняє умові спільності положення відносно системи (14).

Для перевірки лінійної незалежності векторів (13) достатньо перевірити, чи матриця, стовпцями якої є стовпці (12), є невиродженою, тобто

.

Перепишемо формулу (10):

, ,

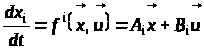де 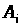, – -і рядки матриць і .

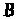Функція Понтрягіна лінійної задачі оптимальної швидкодії має вигляд:

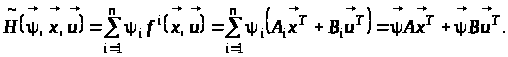(15)

Оскільки перший доданок у формулі (15) не залежить від , то функція досягає максимуму за змінною одночасно з функцією

.

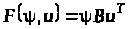Спряжена система у цьому випадку може бути записана у вигляді:

, ,

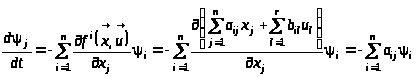або у векторній формі

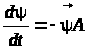. (16)

Позначимо через . З теореми 2 випливає, що якщо 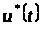– оптимальне керування, то існує такий ненульовий розв’язок системи (16), для якого в кожний момент часу функція набуватиме максимального значення за змінною :

. (17)

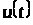Оскільки система (17) з постійними коефіцієнтами не містить невідомих функцій і , то всі її розв’язки можна легко знайти, після чого, використовуючи їх для розв’язання задачі максимізації функції на множині 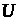, знаходимо оптимальні керування .

Для будь-якого нетривіального розв’язання системи (11) співвідношення (14) однозначно визначає керування 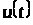, причому це керування кусково стале, а значеннями керування в точках неперервності є вершини багатогранника .

Точки розриву оптимальної функції керування 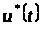відповідають зміні значення керування і називаються точками перемикання. Якщо – точка перемикання, то ліворуч від неї керування має одне значення, наприклад, , а праворуч інше – .

Позначимо через підмножину у 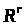виду

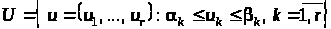. (18)

Якщо всі корені характеристичного рівняння матриці з (14) є дійсними, то для будь-якого розв’язання рівняння (18) кожна з функцій є кусково сталою і має не більше ніж перемикань ( – порядок системи (16)).

Керування 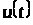називається екстремальним керуванням, якщо воно задовольняє принципу максимуму.

Для лінійної задачі оптимальної швидкодії з областю керування – багатогранником 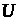керування 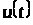є екстремальним, якщо існує таке нетривіальне розв’язання системи (17), для якого матиме місце співвідношення (18).

Зрозуміло, що будь-яке оптимальне керування є екстремальним. Тому, щоб знайти оптимальне керування, що переводить фазову точку зі стану у стан , треба відшукати всі екстремальні керування з цими крайовими умовами, а потім серед них вибрати те, що здійснює перехід за найменший час.

У загальному випадку можуть існувати кілька оптимальних керувань, що переводять фазову точку зі стану у стан , але якщо початок координат у просторі керувань є внутрішньою точкою багатогранника , то екстремальне керування єдине. Отже, у лінійних задачах оптимальної швидкодії принцип максимуму дозволяє не тільки визначити вид оптимальних керувань, але й одержати умови єдиності оптимального керування.

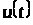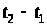Припустимо, що початок координат є внутрішньою точкою багатогранника припустимих керувань. Якщо і – два екстремальних керування, що переводять фазову точку зі стану у стан за час і відповідно, то і , .

У теоремі має місце умова .

Теорема. Якщо існує хоча б одне керування, що переводить систему (17) зі стану у стан , то існує й оптимальне по швидкодії керування, що також переводить систему з у .

4. Умови оптимальності у задачі з рухомими кінцями

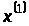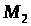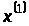У задачі з рухомими кінцями або початковий стан , або кінцевий стан , або обидва ці стани невідомі. Задані тільки множини і , що містять точки та .

Гіперповерхня – це множина всіх точок 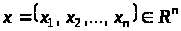, які задовольняють співвідношенню

,

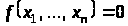де 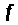– скалярна диференційована функція. Якщо 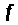– лінійна функція, то гіперповерхня називається гіперплощиною і описується рівнянням

. (19)

Якщо 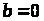, то гіперплощина (19) є ()-вимірним лінійним підпростором в .

Будь-який ()-вимірний підпростір може бути заданий як множина розв’язань лінійної однорідної системи з рівнянь із невідомими, матриця якої має ранг :

.

Такий лінійний підпростір називається -вимірною площиною. Множина розв’язань системи нелінійних рівнянь

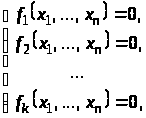
де функції , …, диференційовані і ранг матриці Якобі цієї системи функцій дорівнює , є -вимірним гладким різноманіттям.

Задача оптимального керування з рухомими кінцями полягає в тому, щоб знайти таке припустиме керування 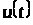для системи із законом руху

, , ,

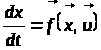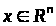яке переводить фазову точку з деякого, заздалегідь невідомого, стану на -вимірному різноманітті () у деякий стан 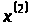на -вимірному різноманітті 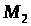() і надає найменшого значення функціоналу

.

Задача оптимального керування з фіксованими кінцями є окремим випадком цієї задачі при , тобто коли різноманіття і 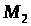вироджуються в точку.

Відсутність рівнянь, що задають початковий і кінцевий стани, приводить до того, що система необхідних умов перестає бути повною. У цьому разі для одержання відсутніх рівнянь використовують умови, що називаються умовами трансверсальності.

Умови трансверсальності. Вектор спряжених змінних із принципу максимуму задовольняє умові трансверсальності на лівому кінці траєкторії , якщо вектор ортогональний дотичній площини до різноманіття в точці , тобто

, (20)

де – довільний вектор, що лежить у дотичній площини. Аналогічно формулюється умова на правому кінці.

Якщо , – оптимальний процес у задачі з рухомими кінцями , , то ненульова вектор-функція , що існує відповідно до теореми 3, задовольняє на кожному з кінців траєкторії умовам трансверсальності.

Розглянемо окремий випадок задачі з рухомими кінцями, коли, наприклад, правий кінець траєкторії вільний (тобто 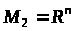). Тоді умови трансверсальності зводяться до співвідношення . Повний вектор спряжених змінних

визначається з точністю до довільної сталої, зокрема, вважають, що 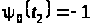(відповідно до принципу максимуму , 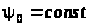) і тоді

.