Модель биполярного транзистора

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

КАФЕДРА РЭС

РЕФЕРАТ

НА ТЕМУ:

«Модель биполярного транзистора»

МИНСК, 2009

В данной программе реализованы две классические модели, описывающие характеристики биполярного транзистора (БТ) при работе на постоянном токе и в режиме "большого сигнала". Это модель Эберса-Молла и зарядовая модель Гуммеля-Пуна.

Модель Эберса-Молла основана на суперпозиции нормального и инверсного БТ, работающих в активном режиме. Такой подход к моделированию обусловлен тем, что при управлении "большим сигналом" БТ работает в двух режимах:

активном - нормальном режиме работы БТ, при котором рабочий ток обусловлен инжекцией носителей заряда из эмиттера (emitter) в базу (base);

насыщения - режим: работы БТ, при котором рабочий ток обусловлен инжекцией из коллектора (collector) в базу. В этом режиме р-п -переходы меняются ролями и в связи с этим изменяется направление протекания выходного тока на противоположное - инверсное.

Модель Эберса-Молла связывает токи на выводах БТ с напряжениями на р-п - переходах, поэтому она удобна для схемотехнического анализа.

Однако модель Эберса-Молла не учитывает некоторые эффекты, сопровождающие работу БТ в широком диапазоне изменения рабочих токов и напряжений.

Зарядовая модель Гуммеля-Пуна фактически дополняет модель Эберса-Молла выражениями связывающими токи инжекции с зарядом в базе. Эти выражения, в частности, позволяют учесть зависимость коэффициента передачи тока от рабочих токов и напряжений Эквивалентная схема модели БТ по постоянному току и для режима "большого сигнала" приведена на рис28.4. Элементы эквивалентной схемы, приведенной на рис 4, моделируют:

- генераторы тока I_>B> и I_>C>, управляемые напряжениями соответственно - статические ВАХ БТ;

- элементы накопления заряда Q_>BE> и Q_>BC> - накопление заряда вблизи соответствующих р-п-переходов (между соответствующими электродами) БТ;

- резисторы R_>B> , R_>C> R_>E> - омические сопротивления областей базы, коллектора и эмиттера соответственно.

Генератор тока I_>B> моделирует ток, протекающий в цепи базы (через электрод базы) в двух режимах работы активном (нормальном, прямом -forward) и насыщения (инверсном - reverse) и описывается выражением

(1)

где I_>B>^F и I_>B>^R - токи базы в прямом и инверсном включении БТ.

При моделировании генераторов тока I_>B> и I_>С> следует учитывать токовую зависимость коэффициентов передачи БТ, которая в режиме малых токов обусловлена суперпозицией двух физических эффектов, определяющих величину тока базы: генерация (инжекция) и рекомбинация носителей заряда. Эти эффекты имеют место в прямом и инверсном, включении и потому выражение (1) Можно представить в следующем виде:

(2)

где - составляющие тока базы, обусловленные инжекцией (injection) и рекомбинацией (recombination) носителей заряда в прямом и инверсном включениях соответственно.

В режиме малых (менее 1 мА) токов коллектора зависимость коэффициента передачи тока от тока коллектора B(I_>С>) имеет вид, представленный на рис.1. Спад коэффициента В в режиме малых токов объясняется с помощью ВАХ, генераторов тока базы I_>B> и коллектора I_>С>, представленной на рис.2. Из данной ВАХ видно, что при токах I_>С> больше некоторого тока I_>L>, графики I_>С> (V_>be>) и I_>B> (V_>be>) параллельны, что и обеспечивает постоянство коэффициента В (см рис.5), определяемого отношением тока I_>С> к I_>B>. При I_>С> меньше I_>L> большой вклад в ток I_>B> вносит составляющая I_>BR>, зависимость Ibr(Vbe) которой имеет наклон, отличный от зависимости I_>С> (V_>BE>), и поэтому коэффициент В при уменьшении V_>BE>, a соответственно и тока I_>С>, падает.

Рис.1. Зависимость коэффициента передачи тока от тока коллектора

Рис. 2. ВАХ генераторов тока I_>С> и I_>B>

В передаточной модели Эберса-Молла инжекционные составляющие тока базы, протекающие в прямом и инверсном включениях БТ, описываются через выходной ток для прямого I^F и инверсного I^R включений и соответствующие этим включениям коэффициенты передачи тока B^R и B^F. C учетом изложенного для токов I_>BI>^F и I_>BI>^R можно записать

	(3)
	(4)

В передаточной модели Эберса-Молла токи I^F и I^R описываются следующими выражениями

	(5)
	(6)

где I_>S> – начальное значение тока инжекции неосновных носителей в базу, которое в программе PSPICE определяется следующим образом

	(7)
	(8)

Из выражений (5) и (6) следует, что для расчета токов I^F я I^R используется одно начальное значение этих токов. Это может быть объяснено тем, что эти токи обусловлены инжекцией носителей заряда в одну и ту же область - область базы БТ. Такое допущение упрощает модель благодаря уменьшению ее параметров. Однако вносит неточность в расчет, так как инжекция и прохождение носителей заряда в базе, обусловленные двумя механизмами - диффузией и дрейфом под действием электрического поля - Неодинаковы в различных направлениях по базе. Диффузия носителей заряда через р-п-переход прямо пропорциональна градиенту (перепаду) их концентрации вблизи соответствующего р-п-перехода. Градиент концентрации носителей заряда у эмиттерного р-п-перехода интегрального п-р-п БТ всегда выше, чем у коллекторного.

Кроме того, в базе такого транзистора, сформированной методом диффузии, вследствие наличия градиентов концентраций легирующей примеси и основных носителей заряда из-за диффузии последних произойдет перераспределение зарядов и образуется электрическое поле. Это поле является ускоряющим для электронов, инжектированных из эмиттера в базу, и тормозящим для электронов, инжектированных из коллектора в базу.

Подставив (3)...(6) в (2), получим выражение для ВАХ генератора тока I_>B>:

(9)

Где N_>e> и N_>с> - коэффициенты неидеальности ВАХ генератора тока базы, обусловленной рекомбинацией носителей заряда, в прямом и инверсном включениях соответственно,

- начальные значения рекомбинационных составляющих тока базы в прямом и инверсном включениях соответственно.

Генератор I_>C> моделирует токи, протекающие в цепи коллектора (через электрод коллектора) в прямом и инверсном включении и согласно передаточной модели Эберса-Молла может быть описан выражением

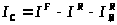
(10)

В выражении (10) первое слагаемое описывает ток через электрод коллектора в прямом включении. Второе и третье слагаемые в сумме дают Ток, протекающий через электрод коллектора в инверсном включении.

Зарядовая модель Гуммеля-Пуна дополняет передаточную модель Эберса-Молла введением некоторого заряда в базе Q_>b> в модель для генератора тока Iс, что позволяет описать два хорошо известных на практике эффекта: зависимость I_>C>(V_>CE>) в активной области выходной ВАХ БТ и спад коэффициента передачи тока при высоких уровнях тока I_>C> В модели Гуммеля-Пуна выражение (10) имеет следующий вид:

(11)

Подставив в (10) выражения (5), (6), с учетом (1), (2) и (9) получим:

(12)

где Q_>B> - зарядовый коэффициент.

График зависимости Ic(Vce) (выходной ВАХ) приведен на рис.7. Рост тока I_>C> при увеличении V_>CE> активной области ВАХ обусловлен уменьшением толщины квазинейтральной базы (эффект Эрли). С ростом обратносмещающего потенциала на коллекторе увеличивается толщина обедненной области р-п - перехода коллектор - база и уменьшается толщина квазинейтральной базы. Хорошо известно, что при уменьшении толщины базы и неизменном потенциале на базе ток I_>C> растет.

Из графика зависимости В(I_>C>), приведенного на рис.5, видно, что при токе I_>C> больше некоторого значения I_>K> происходит спад коэффициента В. Уменьшение коэффициента В объясняется тем, что при больших токах I_>C> и соответственно высоких концентрациях подвижных носителей заряда растет плотность заряда в р-п-переходе коллектор - база и как следствие этого уменьшается его ширина (эффект Кирка). Сужение р-п - перехода коллектор-база приводит к увеличению толщины квазинейтральной базы, а это в свою очередь - к уменьшению коэффициента В.

Таким образом, рост тока I_>C> в активной области выходной ВАХ, а также спад коэффициента В при больших токах I_>C> связаны с изменением толщины квазинейтральной базы. В то же время при изменении толщины базы и постоянной концентрации основных носителей заряда в ней изменяется заряд в базе. Такая модуляция заряда в базе и используется в модели Гуммеля-Пуна для моделирования рассмотренных выше эффектов. При этом изменение заряда в базе оценивается с помощью зарядового коэффициента Q_>b>, который представляет собой отношение концентрации основных носителей в базе к заряду в базе при нулевых смещениях на р-п-пререходах. То есть при напряжениях V_>CE> =0, V_>BC> =0 коэффициент Q_>b>=1.

Поскольку с помощью коэффициента Q_>b> моделируются два рассмотренных выше эффекта, то в свою очередь он зависит от двух других зарядовых коэффициентов и описывается выражением

(13)

Где Q_>1> - зарядовый коэффициент, моделирующий зависимость тока Iс от выходного напряжения в активной области выходной ВАХ;

Q_>2> - зарядовый коэффициент, моделирующий спад зависимости В(Iс) при больших токах Iс

Зарядовый коэффициент Q_>1> в прямом и инверсном включениях моделируется выражением

(14)

где V_>A> и V_>B> напряжения Эрли в прямом и инверсном включениях.

Зарядовый коэффициент Q_>2> в прямом и инверсном включениях моделируется выражением

(15)

где: I_>K> и I_>K>^R - значения тока I_>C>, при которых в прямом и инверсных включениях начинается спад зависимости В(I_>C>) (см. рис.5).

Резисторы Re, Rc и Rb моделируют сопротивления тех частей эмиттера, коллектора и базы, по которым протекают (растекаются) соответствующие токи. В рассматриваемой модели сопротивления резисторов Re и Rc считаются постоянными и от режимов работы по току и напряжению не зависят (не моделируются).

Резистор Rb моделирует сопротивление квазинейтральной базы (ее проводящей части), расположенной под эмиттером ("активная база"). Сопротивление остальной части базы (пассивная база), подключенной последовательно, сравнительно мало, так как она легирована сильнее, чем "активная база". Сопротивление "активной базы" зависит от толщины ее проводящей части, а, следовательно, с учетом эффектов Кирка и Эрли, от режимов работы по току и напряжению. Эта зависимость моделируется с использованием зарядового коэффициента Q_>B>

(16)

где Rso - сопротивление области базы при напряжениях V_>BE>_>=> V_>BC> =0. Элементы накопления заряда Q_>BE> и Q_>BC>_> >моделируют накопление заряда в обедненной области р-п-переходов база-эмиттер и база-коллектор и заряда неосновных носителей, инжектированных в базу. Эти элементы эквивалентны емкостям р-п - переходов база-эмиттер Све и база-коллектор C_>BC>, зависящим от соответствующих напряжений. Эти емкости по аналогии с емкостью диода состоят из барьерных емкостей соответствующих р-п - переходов и диффузионных емкостей, обусловленных инжектированными в базу неосновными носителями заряда. ВФХ этих элементов в прямом и инверсном включениях моделируются следующими выражениями:

- элемент Qbe

	(17)
	(18)

- элемент Qbc

	(19)
	(20)

Где τ^F и τ^R – времена существования (времена жизни или прохождения) неосновных носителей заряда л базе в прямом и инверсном включениях; - коэффициент резкости и контактная разность потенциалов р-п - перехода база-эмиттер;

M_>E> и φ_>BE> – коэффициент резкости и контактная разность потенциалов р-п - перехода база-коллектор;

Хс - коэффициент, определяющий часть барьерной емкости р-п-перехода база - коллектор, которая подключена к электроду базы через резистор R_>B>.

С помощью коэффициента Хс р-п - переход база-коллектор и его емкость С_>BC> разбиваются на две части: одна подключается к электроду базы через резистор R_>B>, а другая - непосредственно к этому электроду. Такое разбиение обусловлено тем, что, как было сказано выше, резистор R_>B> моделирует сопротивление "активной базы", расположенной между донной частью эмиттера и коллектором. То есть с ней соприкасается только часть р-п - перехода база - коллектор. Остальная часть этого р-п - перехода соприкасается с "пассивной базой", сопротивлением которой пренебрегают, и поэтому эта часть р-р-перехода накоротко соединена с электродом базы. Такое разбиение р-п-перехода база-коллектор при моделировании его емкости повышает достоверность моделирования частотных характеристик БТ.

Переход база - эмиттер и его емкость не разбиваются на части по-видимому потому, что через боковую "пассивную" часть этого р-п -перехода токи эмиттера и базы практически не протекают (очень малы) и ее емкость исключается из рассмотрения. То есть емкость С_>ве >оценивает накопление заряда в "активной" части р-п-перехода и заряд в "активной базе".

Малосигнальная модель биполярного транзистора

Рассмотренная выше модель используется для анализа характеристик БТ по постоянному току и в режиме "большого сигнала" Для анализа частотной зависимости передаточных (усилительных) характеристик в рамках анализа по переменному току (напряжению) используются малосигнальные модели БТ, в которых нелинейные элементы: генераторы токов I_>B> и I_>C> элементы накопления заряда Q_>BC>_> >и Q_>BE> резистор R_>B>, характеристики которых зависят от величины входного управляющего сигнала, заменяются линейными элементами.

Анализу по переменному току (напряжению) всегда предшествует анализ по постоянному току (напряжению), а точнее, расчет "рабочих точек",то есть расчет потенциалов в узлах (на электродах ЭРЭ) и токов в цепях анализируемой схемы при подключении к ней только источника питающего напряжения. Это необходимо для того, чтобы определить эквивалентной схемы ЭРЭ, которые остаются неизменными при последующем подключении входного малосигналыюго источника переменного управляющего напряжения и проведения анализа частотных характеристик схемы. Таким образом, нелинейные элементы эквивалентной схемы становятся линейными, то есть обеспечивают линейную связь между переменным напряжением, приложенным к ним, и переменным током, через них протекающим.

Элементы этой эквивалентной схемы моделируют:

резисторы R_>B>, R_>E>, R_>C> – то же, что и в эквивалентной схеме модели "большого сигнала";

конденсаторы С_>π> и С_>μ> - емкости р-п - переходов база – эмиттер и база-коллектор, которые соответственно равны их значениям в рабочих точках (р.т.),то есть

	(21)
	(22)

проводимости С_>π> и С_{>μ –}> проводимости генератора тока базы в прямом

(23)

в инверсном

(24)

включениях;

- проводимость G_>C> – проводимость генератора тока коллектора в прямом и инверсных включениях

(25)

Шумовая модель биполярного транзистора

При анализе частотных зависимостей передаточных характеристик в рамках анализа по переменному току линейных (усилительных) ИС может проводиться и анализ шумовых характеристик.

Эквивалентная схема шумовой модели дополнительно к элементам эквивалентной схемы малосигнальной модели содержит генераторы шумовых токов, включенных параллельно источникам шума (рис.29.3).

В приведенной эквивалентной схеме генераторы шума моделируют:

- генераторы тока I_>NRB>, I_>NRC>, I_>NRE> - тепловые шумы резисторов R_>B>, R_>C>_>,> R_>E> соответственно и описываются уравнениями:

	(26)
	(27)
	(28)

- генераторы I_>NC>, и Inb – дробовой и фликер-шумы генераторов тока I_>C> и I_>B> соответственно и описываются уравнениями:

	(29)
	(30)

где K_>f>_> >и α_>f>- коэффициенты фликер-шума,

f- частота переменного входного сигнала.

Температурная модель биполярного транзистора

В программе PSPICE моделируются следующие температурные зависимости параметров БТ:

- начального значения тока инжекции в базу I_>S>(T) (моделируется так же, как начальное значение тока диода (14));

Рис. 3. Эквивалентная схема шумовой модели БТ

Рис. 4. Эквивалентная схема ПТУП

- начального значения рекомбинационной составляющей тока базы в прямом включении

(31)

где X_>TB> - коэффициент температурной зависимости коэффициента передачи тока,

X_>T>_>1> - коэффициент температурной зависимости начального тока; -начального значения рекомбинационной составляющей тока базы в обратном включении I^R_>BRO>(Т) (моделируется аналогично I^F_>BRO>(Т), только вместо параметра N_>E> в выражение (48) подставляется Nc)', - коэффициента передачи тока в прямом включении

(32)

– коэффициента передачи тока в обратном включении B^R(T) (моделируется аналогично B^F(T), только вместо B^F в выражение (49) подставляется B^R

–контактных разностей потенциалов р-п - переходов база-эмиттер φ_>BE>(t) и база-коллектор φ_>BC>(t) (моделируются так же, как контактная разность потенциалов диода (14), только вместо φ_>J>_> >подставляются φ_>BE> или φ_>B>_>С> соответственно);

емкостей р-п - переходов база-эмиттер Све(Т) и база-коллектор Свс(T) (моделируются так же, как емкость р-п - перехода диода (15) только вместо C_>JO> подставляются Сbe или Сbс соответственно;

-коэффициентов фликер-шума К_>f>(Т) и а_>f>(Т) (моделируются аналогично диоду).

ЛИТЕРАТУРА

1. Новиков Ю.В. Основы цифровой схемотехники. Базовые элементы и схемы. Методы проектирования. М.: Мир, 2001. - 379 с.

2. Новиков Ю.В., Скоробогатов П.К. Основы микропроцессорной техники. Курс лекций. М.: ИНТУИТ.РУ, 2003. - 440 с.

3. Пухальский Г.И., Новосельцева Т.Я. Цифровые устройства: Учеб. пособие для ВТУЗов. СПб.: Политехника, 2006. - 885 с.

4. Преснухин Л.Н., Воробьев Н.В., Шишкевич А.А. Расчет элементов цифровых устройств. М.: Высш. шк., 2001. - 526 с.

5. Букреев И.Н., Горячев В.И., Мансуров Б.М. Микроэлектронные схемы цифровых устройств. М.: Радио и связь, 2000. - 416 с.

6. Соломатин Н.М. Логические элементы ЭВМ. М.: Высш. шк., 2000. - 160 с.