Расчёт переходных процессов в линейных электрических цепях с сосредоточенными параметрами
Министерство Образования Украины
Кафедра электротехники
Курсовая работа
по курсу “Теория электрических и электронных цепей”
на тему “Расчёт переходных процессов в линейных электрических цепях с сосредоточенными параметрами”
Вариант № 12
Содержание курсовой работы
1. В электрической цепи, (схема которой представлена на рис.1, а параметры цепи приведены в таблице 1, причём R>4>=R>3> ), происходит переходной процесс. На входе цепи действует постоянное напряжение величиной Е>m>.
2. Классическим методом расчёта найти выражения для мгновенных значений всех токов цепи и напряжений на реактивных элементах после коммутации. Построить графики изменения этих величин в одних осях. Графики изменения построить на интервале, равном времени переходного процесса t>nn>.
Это время определить по следующим формулам:
t
 >nn>=
>nn>=
 или t>nn>=
или t>nn>=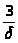
где λ>min> – наименьший из двух вещественных корней;
δ - вещественна часть комплексного корня.
3. Операторным методом расчёта найти выражение для тока в катушке индуктивности.
4. На входе цепи (рисунок 1) действует источник, напряжение которого меняется по синусоидальному закону
e(t)=E>m>sin(ωt +φ).
Определить выражение для мгновенного значения тока в катушке индуктивности.
Построить график переходного процесса тока катушки индуктивности.
5.На входе цепи,(рисунок 2) действует источник, напряжение которого меняется по закону(заданное графиком 1). Найти выражение для величины, указанной в 17-м столбце таблицы исходных данных (таблица 1). Построить совместные графики измерения заданного напряжения и искомой величины. В таблице исходных данных даны абсолютные значения напряжений U>0, >U>1,> U>2, >U>3. >Принимая значение времени: t>1>=τ , t>2>=1,5τ , t>3>=2τ , t>4>= 2,5τ .
Здесь τ – постоянная времени рассматриваемой цепи.
Таблица 1:
|
Номер варианта |
Номер схемы |
Параметры источника |
Параметры цепи |
Параметры источника для интеграла Дюамеля |
Номер схемы по рисунку 2 |
Исследуемая величина ƒ(t) |
||||||||||
|
Напряжение U, В |
Частота ƒ, Гц |
Нач. фаза φ,град. |
R1 Ом |
R2 Ом |
R3 Ом |
L мГн |
C мкФ |
№ графика |
Uо В |
U1 В |
U2 В |
U3 В |
||||
|
12 |
12 |
70 |
30 |
75 |
26 |
10 |
10 |
100 |
25 |
12 |
20 |
5 |
10 |
0 |
4 |
UR2 |
Р
R>1>
исунок 1:



R>2>




C
L


t=0










R>3>
Рисунок 2:








i>1>
R>1>
R>3>
R3




C
R>2>



U(t)
i>2>





i>c>
Г
U

 рафик 1:
рафик 1:
U>0>


t
t>2>
t>3>
0

t>1>



U>1>> >

U>2>
1 этап курсовой работы
Расчет цепи с двумя реактивными элементами в переходных процессах классическим методом
R>1>






i>1>


i>2>
R>2>


C


L
t=0


i>c>







R>3>



1 этап
Запишем начальные условия в момент времени t>(-0) >
i >2(-0)>=i>1(-0)>=
>2(-0)>=i>1(-0)>= =
= =
1.52 (A)
=
1.52 (A)
U>c(-0)>= i>2>.R>2>=U>c(+0)>
Напишем уравнения по законам Кирхгофа для цепи:
i>1>-i>2>-i>c>=0 (1)
i >1>.R>1>+
i>2>.
R>2>+L
>1>.R>1>+
i>2>.
R>2>+L =U
(2)
=U
(2)
i>1>.R>1>+ U>c>=U (3)
Из (2) уравнения выразим i>1 >
i>1>=>
>
 >
>(2.1)
>
>(2.1)
i>1> из уравнения (2.1) подставим в (1) и выразим i>c>
i>c>= >
>(1.1)
>
>(1.1)
i>1> подставим в (3) и выразим U>c>
U= (3)
(3)
U>c>=U-U-
i>2>.
R>2>->
>
 >
>(3)
>
>(3)
U>c>=i>2>.R>2>+ >
>(3.1)
>
>(3.1)
U>c>=>
>
 >
>
>
>
 >
>(3.2)
>
>(3.2)
Подставим в место U>c >и i>c >в> >уревнение (3.2), получим:
 (3.3)
(3.3)
Продифференцируем уравнение (3.3) и раскроем скобки:

 (3.4)
(3.4)
В дифференциальном уравнении(3.4) приведём подобные слогаемые:

2 этап
Во втором этапе мы решим дифференциальное уравнение относительно i>2>, для этого мы представим i>2> как сумму двух составляющих i>2св >– свободная составляющая и i>2вын> – вынужденная составляющая
i>2>=i>2св>+i>2вын>
i>2вын >найдём по схеме
i>2вын>=
i>2св>
найдём из дифференциального уравнения
подставив численные значения в уравнение
и заменив
 через
,
а
через
,
а
 через
2
получим:
через
2
получим:
L2+R>2>+ +
+ =0
(3.5)
=0
(3.5)
Решим характеристическое уравнения (3.5) найдя его корни >1> и >2>
0.12+10+ +
+
15384,6+153,85+40000+10+0,12=0
Д=b2-4ac=(163,85)2-4.0,1.55384,6=26846,82-22153,84=4692,98
 >1,2>=
>1,2>= ;
;
 ;
;
 >1>
>1> >2>
– вещественные
>2>
– вещественные
>1>=


>2>=

i>2св>=А>1>е-477t+А>2>е-1162t (3.6)
i>2>=1.94+ А>1>е-477t+А>2>е-1162t (3.7)
3 этап
Найдём А>1> и А>2> исходя из начальных условий, законов коммутации и на основании системы уравнений Кигхгофа записаных на 1 этапе.
Найдём ток i>2> для момента времени t = +0. Для этого продифференцируем уравнение (3.6) при t=0.
i>2(+0)>=i>2вын(+0)>+ А>1>+А>2>
 -477
А>1>-1162
А>2>
-477
А>1>-1162
А>2>
Из уравнения (2) найдём
 для
момента времени t+0
для
момента времени t+0
 (3.8)
(3.8)
Из уравнения (3) выразим i>1> для момента времени t+0 при U>c>=i>2>R>2>
i>1>= (3.9)
(3.9)
Найдём
 подставив значение i>1>
из уравнения (3.9) в уравнение (3.8)
подставив значение i>1>
из уравнения (3.9) в уравнение (3.8)
 (4.0)
(4.0)
Подставим
значение
 ,
i>2(+0)>,
i>2вын>
в систему и найдём коэффициенты А>1>
и А>2>
,
i>2(+0)>,
i>2вын>
в систему и найдём коэффициенты А>1>
и А>2>
1 ,52=1,94+
А>1>
+ А>2
>(4.1)
,52=1,94+
А>1>
+ А>2
>(4.1)
2=-477 А>1>-1162 А>2 >(4.2)
Из уравнения (4.1) выразим A>1> и подставим в (4.2)
А>1>=-0,42-А>2>
2=-477(-0,42-А>2>)-1162А>2> (4.3)
Из уравнения (4.3) найдём А>2>
2=200,34+477А>2>-1162А>2>
2=200,34-685А>2>
А>2>=
А>1>=-0,42-0,29=-0,71
Подставим найденные коэффициенты А>1> и А>2> в уравнение (3.7)
i>2>=1,94-0,71е-477t+0,29е-1162t (А)
4 этап
Определяем остальные переменные цепи U>L>, U>c>, i>c>, i>1>
U>L>= (В)
(В)
U>c>=
 +i>2>R>2>=
+i>2>R>2>=

=
 (В)
(В)
i>c>= (А)
(А)
i>1>=i>c>+i>2>=(0,044е-477t+0,014е-1162t)+( 1,94-0,71е-477t+0,29е-1162t) =
=1,94-0,666е-477t+0,304е-1162t (А)
Построим графики изменения найденных величин в одних осях. Графики изменения построим на интервале, равном времени переходного процесса t>nn>.
Это время определим по формуле:
t
 >nn>=
>nn>=

Найдём t>пп> время переходного процесса
t>пп>= (с)
(с)
Таблица переменных
-
Время переходного процесса tnn (c)
Значение тока
i1
(A)
Значение тока
i2
(A)
Значение тока
ic
(A)
Значение напряжения
UL
(B)
Значение напряжения
UC
(B)
0.000
1.578
1.520
0.058
0.20
15.22
0.001
1.622
1.590
0.032
10.49
16.95
0.002
1.713
1.695
0.018
9.75
17.92
0.003
1.790
1.779
0.011
7.07
18.50
0.004
1.844
1.837
0.006
4.70
18.84
0.005
1.879
1.875
0.004
3.02
19.06
0.006
1.902
1.899
0.0025
1.90
19.19
0.0063
1.907
1.905
0.0022
1.65
19.21
Рисунок 3 - График токов

где


 i>1
>
i>2>
i>c>
i>1
>
i>2>
i>c>
Рисунок 4 – График напряжений

где

 U>L>
U>C>
U>L>
U>C>
2 этап курсовой работы
2. Найдём выражение для тока в катушке при действии в цепи источника синусоидального напряжения:
e
R>2>
(t)=E>m>sin(t+) 

 R>1>
R>1>



i>1>

i>3>


R>3>

C
U(t)



L

i>2>



R>3>


где E>m>=100 (B)
=2f
 =2 3,14 50=314 (Гц)
=2 3,14 50=314 (Гц)
=300
R>1>=R>2>=10 (Ом) L=100 (мГн)
R>3>=9 (Ом) С=100 (мкФ)
=314 (Гц)
X>L>=L=314. 0,1=31,4 (Ом)
X>C>= (Ом)
(Ом)
Найдём начальные условие:
U(t)=U>m>sin(t+)=100sin(314+30);
U>m>=100ej30=86,603+j50 (В)
U>C(-0)>=0 (B)
Найдём полное сопротивление цепи
Z>п>=R>1>+R>3>+jX>L>=10+9+j31,4=19+j31,4 (Ом)
Зная сопротивление и напряжение найдём I>3m>
I>3m>=I>1m>=
 (А)
(А)
Найдём мгновенное значение тока
i>3>(t)=I>3m>sin(t+)=2.725sin(314t-28.82) (A)
Для времени t=0 ток будет равен
i>3(-0)>=2.725sin(-28.82)=-1.314 (A)6 (A)
Таким образом
U>C(-0)>=U>C(+0)>=0 (B)
i>3(-0)>= i>3(+0)>=-1.314 (A)
1 этап
Напишем уравнения по законам Кирхгофа для цепи:
i >1>-i>2>-i>3>=0
(1)
>1>-i>2>-i>3>=0
(1)
i>1>.R>1>+
i>3>.R>3>+L =U(t)
(2/)
=U(t)
(2/)
i>1>.R>1>+i>2>.R>2>+U>c>=U(t) (3/)
Из (2/) уравнения выразим i>1 >
i>1>=>
>
 >
>(2/.1)
>
>(2/.1)
i>1> из уравнения (2/.1) подставим в (1/) и выразим i>2>
i>2>= >
>(1/.1)
>
>(1/.1)
U(t)=U(t)-i>3>.R>3>-L +R>2
+R>2 >
>

- (3.1)
(3.1)
Продифференцируем уравнение (3.1) раскроем скобки и приведём подобные слагаемые:
 (3.2)
(3.2)
2 этап
Вид решения для i>3св> при действии в цепи источников постоянного и переменного напряжений одинаков, так как в однородном дифференциальном уравнении отсутствует параметр U, а значит, вид i>3св> не зависит от входного напряжения.
Таким образом, выражение, которое было найдено в 1этапе, будет иметь следующий вид:
i>3св>=А>1>е-406t+А>2>е-234t
Теперь найдём вынужденную составляющую тока катушки i>3вын>
i>3вын> находим для цепи в послекоммутационном режиме. Расчёт параметров схемы при действии e(t);
Найдём вынужденную составляющую амплитудного тока I>1>, а для этого найдём Z>п вын> сопротивление цепи:
Z>п>>
>>вын>= (Ом)
(Ом)
I>1m>= (A)
(A)
Найдём U>ab вын>
U>ab m>=
I>1m>> >>
>(В)
>>
>(В)
I>3 m>=
 (A)
(A)
Найдём i>3 вын>
I>3 >>вын>= I>3 m>sin(t+)=2.607sin(314t-43.60) (A)
Таким образом
i>3>=2.607sin(314t-43.60)+А>1>е-406t+А>2>е-234t
3/ этап
Найдём А>1> и А>2> исходя из начальных условий, законов коммутации и на основании системы уравнений Кигхгофа записаных на 1/ этапе.
i >3>=2.607sin(314t-43.60)+А>1>е-406t+А>2>е-234t
>3>=2.607sin(314t-43.60)+А>1>е-406t+А>2>е-234t

i>3(+0)>=i>3(-0)>=-1.314 (A)
i >3(+0)>=2.607sin(-43.60)+A>1>+A>2>=-1.798+A>1>+A>2>
>3(+0)>=2.607sin(-43.60)+A>1>+A>2>=-1.798+A>1>+A>2>


R>1>i>1>=U(t)-R>2>i>2>-U>C>


 =
=

=

Подставим значение
 ,
i>3(+0)>,
и найдём коэффициенты А>1>
и А>2 >для
времени t+0
,
i>3(+0)>,
и найдём коэффициенты А>1>
и А>2 >для
времени t+0
 -1.314=-1.798+A>1>+A>2>
-1.314=-1.798+A>1>+A>2>
433.96=592/806-406A>1>-234A>2>
A>1>=-1.314+1.798-A>2>=0.484- A>2>
433.96=592.806-406(-0.484- A>2>)-234 A>2>
433.96-592.806+406 .0.484= A>2>(406-234)
3 7.658=172A>2>>
> A>2>=0.219
7.658=172A>2>>
> A>2>=0.219
A>1>=0.265
Ток i>3> будет равняться
I>3>=2.607sin(314t-43.600)+0.265е-406t+0.219е-234t (A)
Таблица переменных
-
Время t, c
0.000
0.001
0.002
0.003
0.004
0.005
0.006
0.0063
Ток i2, A
1.115
1.327
1.528
1.671
1.7428
1.7430
1.6745
1.6413

3 этап курсовой работы
Найдём выражение для тока катушки операторным методом:


 R>1>
R>1> R>2>
R>2>



i>1>

i>3>


R>3>

C
U



i>2>
L






Запишем начальные условия в момент времени t>(-0)>
I >3(-0)>=
>3(-0)>= =
= =
5.263 (A)
=
5.263 (A)
U>c(-0)>=0 (В)
Нарисуем схему замещения цепи для расчёта тока катушки операторным методом.
В ветви с реактивными элементами добавим ЭДС, так как у нас не нулевые начальные условия. Причём в ветвь катушки по на правлению тока, а в ветвь конденсатора против тока.
R>1>
R>2>









I>1>(p)


I>3>(p)

R>3>




Lp




Li>L(0)>
I>2>(p)







Определим операторное изображение тока катушки. Для этого составим систему уравнений по законам Кирхгофа, направление ЭДС катушки указанo на схеме.
I >1(p)>-I>2(p)>-I>C(p)>=0
(1.3)
>1(p)>-I>2(p)>-I>C(p)>=0
(1.3)
 (2.3)
(2.3)
 (3.3)
(3.3)
Из уравнения (2.3) выразим ток I>1>(p) и подставим в уравнение (3.3):


Из уравнения (3.3)
 (2.3.1)
(2.3.1)
 (2.3.2)
(2.3.2)





Подставим численные значения элементов

По полученному изображению найдём оригинал тока .
Операторное
решение тока имеет вид правильной дроби
I= .
Оригинал тока найдём при помощи теоремы
разложения.
.
Оригинал тока найдём при помощи теоремы
разложения.
Определим корни знамена теля, для этого приняв его равным нулю.
p>1>=0
0,000065p2+0,1065p+36=0
Д =(0б1065)2-4.0,000065.36=0,0019
=(0б1065)2-4.0,000065.36=0,0019



I>2>(p)=
Найдём A>1 >A>2 >A>3>
Коэффициент
A>n>
будем искать в виде,
 где
N(p) – числитель, а M(p) – знаменатель
где
N(p) – числитель, а M(p) – знаменатель
A>1>=
A>2>=
A>3>=
Таким
образом, i>2>(t)
будет равняться

i>2>(t)=A>1>.exp(p>1>t)+ A>2>.exp(p>2>t)+ A>3>.exp(p>3>t)=1,944-0,71e-477t+0,3e-1162t
Искомый ток катушки i>2 >равняется :
i>2>=1,944-0,71e-477t+0,3e-1162t (A)
Токи сходятся.
4 этап курсовой работы
Начертим схему для расчёта цепи интегралом Дюамеля и рассчитаем её








i>1>
R>1>
R>3>
R3




C
R>2>



U(t)
i>2>





i>c>
Определим переходную характеристику h1(t) цепи по напряжению U>R2>. Для этого рассчитаем схему при подключении цепи в начальный момент t=0 к источнику единичного напряжения. Рассчитаем схему классическим методом. Так как нулевые начальные условия U>C(-0)>=U>C(+0)>=0, это значит дополнительных ЕДС не будет.
Напишем уравнения по законам Кирхгофа для цепи:
i >1>-i>2>-i>c>=0
>1>-i>2>-i>c>=0
i>1>.R>1>+
i>2>.R>2>=U
i>с>=
i>с>.R>3>-i>2>.R>1>+U>c>=0 i>1>=i>2>+i>с>
i >1>=i>2>+i>с>
>1>=i>2>+i>с>
> > i>2>(R>1>+R>2>)+i>с>R>1>=U
i>2>=
i>2>(R>1>+R>2>)+i>с>R>1>=U
i>2>=
i>с>.R>3>-i>2>.R>1>+U>c>=0
i>с>.R>3>+U>c>- +
+
ic> >+
>+
 >
> >+
>+
> >+
>+
0 ,00043+1=0
=
-2322,58
(
,00043+1=0
=
-2322,58
( )
)
U>C св>=Ae-2322,58t
U>C
вын>= (B)
(B)
U >C>=U>C
св>+U>C
вын>=0,278+Ae-2322,58t
A=-0,278
>C>=U>C
св>+U>C
вын>=0,278+Ae-2322,58t
A=-0,278
U>C>=0,278-0,278e-2322,58t (B)
i>с>= =25.10-6.0,278.2322,58e-2322,58t=0,016e-2322,58t
(A)
=25.10-6.0,278.2322,58e-2322,58t=0,016e-2322,58t
(A)
U>ab>=i>c>R>3>+U>C>=0,278-0,12e-2322,58t (B)
Таким образом переходная характеристика h1(t) будет равна
h1(t)=U>R2>(t)=0,28-0,12.e-2322,58t (В)
= (c)
(c)
5 этап курсовой работы

U>0>


t
t>2>
t>3>
0

t>1>



U>1>> >

U>2>
Для расчета переходного процесса используем интеграл Дюамеля.
Переходную характеристику h1(t) возьмем из предыдущего этапа
h1(t)=0,28-0,12.e-2322,58t (В)
t>пп>= (c)
(c)
Найдём , t>1>, t>2>, U>1>/(), U>2>/():
= (с)
(с)
t>1>==0.00043 (c) t>2>=1,5=0.00065 (c) t>3>=2=0.00086 (c)
U>0>=20 (В); U>1>=-5 (B); U>2>=-10 (B);
U>1>/()=0
( )
U>2>/()=
)
U>2>/()= (
( )
)
U>3>/()= (
( )
)
Запишем уравнение U>R2>(t) для интервала :

U>R2>=U>0>.h1(t)+ (B)
(B)
-
t (c)
0
0.0001
0.0002
0.0003
0.0004
0.00043
UR2 (B)
3.2
3.697
4.092
4.404
4.652
4.716
Запишем уравнение U>R2>(t) для интервала :

U>R2>=U>0>.h1(t)+
+
-
 (B)
(B)
-
t (с)
0,00043
0.00045
0.0005
0.00055
0.0006
0.00065
UR2 (B)
4,14
3,64
2,37
1,06
-0,27
-1,64
Запишем уравнение U>R2>(t) для интервала :

U>R2>=U>0>.h1(t)+
+ =
=
- )+
)+
+ (B)
(B)
-
t (c)
0.00065
0.0007
0.00075
0.0008
0.00085
0.00086
UR2(B)
-5,145
-4,396
-3,653
-2,914
-2,179
-2,03
Запишем уравнение U>R2>(t) для интервала :

U>R2>=U>0>.h1(t)+
+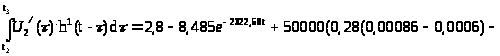
-
+ (B)
(B)
-
t (c)
0.00086
0.0009
0.00095
0.001
0.0013
UR2(B)
-1,97
-1,79
-1,60
-1,42
-0,707
Строим графики U(t) и U>R2>(t) по данным таблиц.