Расчет САУ скоростью электродвигателя постоянного тока независимого возбуждения

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РБ

БЕЛОРУССКАЯ ГОСУДАРСТВЕННАЯ

ПОЛИТЕХНИЧЕСКАЯ АКАДЕМИЯ

КАФЕДРА ЭАПУ и ТК

КУРСОВОЙ ПРОЕКТ

ПО ДИСЦИПЛИНЕ “ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ”

НА ТЕМУ:

РАСЧЕТ САУ СКОРОСТЬЮ

ЭЛЕКТРОДВИГАТЕЛЯ ПОСТОЯННОГО ТОКА

МИНСК

2008

СОДЕРЖАНИЕ

Введение

1.Функциональная схема объекта управления

2.Математическая модель и определение параметров объекта управления

2.1.Математическая модель двигателя

2.2.Математическая модель преобразователя

3.Синтез САУ методом последовательной оптимизации контуров

3.1.Синтез контура регулирования тока

3.1.Синтез статического контура регулирования скорости

3.3.Синтез астатического контура регулирования скорости

4.Синтез САУ методом модального управления

4.1.Синтез САУ без улучшенных динамических показателей

4.2.Синтез САУ скоростью с улучшенными динамическими показателями 5.Синтез САУ с использованием наблюдателя

6.Синтез цифрового управляющего устройства

7.Проектирование принципиальной схемы управляющего устройства

7.1.Расчет принципиальной схемы управляющего устройства, синтезированного методом последовательной оптимизации

7.2.Проектирование принципиальной схемы методом последовательной оптимизации контуров

7.3.Проектирование принципиальной схемы с использованием наблюдателя

Заключение

ВВЕДЕНИЕ

Основная задача управления электроприводами, работающими в режиме пуска, торможения и реверса, состоит в формировании диаграмм тока, обеспечивающей заданное время переходных процессов.

Основное назначение электроприводов, работающих в режиме автоматической стабилизации скорости состоит в автоматическом поддержании скорости или существовании заданного закона изменения скорости с помощью определяемой требованиями технологического процесса. Техническими параметрами подобных систем являются электроприводы механизмов подач металлорежущих станков, обеспечивающих широкий диапазон регулирования и поддержания заданной скорости каждого механизма в отдельности и поддержание заданных соотношений скоростей этих механизмов.

Большинство производственных электроприводов выполняется с наиболее простыми статическими системами регулирования. Для этих систем большое значение имеет получение статических характеристик, обеспечивающих требуемую мощность в установившихся режимах. В современных системах широко применяются астатические системы регулирования, использующие принцип инвариантности.

Для систем стабилизации скорости большое значение имеют показатели качества переходного процесса при возмущающем воздействии.

Режим пуска и торможения являются не основными и к ним в отношении быстродействия не предъявляются повышенные требования.

В особую группу электроприводов следует выделить электрические привода механизмов, для которых в одинаковой степени важны как режим автоматической стабилизации скорости, так и режим пуска и торможения. К этой группе относятся механизмы, в которых время пуска, торможения и реверса соизмеримо со временем установившегося режима движения.

Как правило, структура современного электропривода, работающего в режиме автоматической стабилизации скорости, представляет собой замкнутую контурную систему автоматического регулирования, содержащую главную регулируемую обратную связь и дополнительные обратные связи.

1 ФУНКЦИОНАЛЬНАЯ СХЕМА ОБЪЕКТА УПРАВЛЕНИЯ

В качестве объекта управления используется управляемый полупроводниковый выпрямитель, двигатель постоянного тока независимого возбуждения типа 2ПН-132МУХЛ4. Вал двигателя соединен с тахогенератором.

Выписываем из справочника параметры двигателя:

Pн=2,5кВт

Nн=1000 обмин;

Nм=4000 обмин;

Rя=0,27 Ом;

Rдп=0,2;

Lя.ц=5,7мГн;

Jд. =0,038 кг*м^2.

Вентильный преобразователь представлен апериодическим звеном:

; Tо=0,005с; п=25.

Статические характеристики:

Функциональная схема объекта управления представлена на рис.1.1. Здесь введены следующие обозначения:

- управляемый преобразователь электроэнергии;

- двигатель постоянного тока;

- напряжение управления преобразователем;

- выходное напряжение преобразователя (зависит от );

- угловая скорость электродвигателя.

2 МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И определение ПАРАМЕТРОВ ОБЪЕКТА УПРАВЛЕНИЯ

2.1 МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИГАТЕЛЯ

С
хема замещения электродвигателя представлена на рис.2.1.

На основании второго закона Кирхгофа для схем замещения можно записать уравнение:

(2.1)

где .

На основании уравнения динамики:

(2.2)

где – полный момент

- статический момент

- суммарный момент инерции двигателя

- угловая скорость электродвигателя

При постоянном магнитном потоке () справедливо:

;

где - конструктивные постоянные электродвигателя, которые в системе СИ отличаются на 2% т.е. их можно считать равными.

Подставив в уравнение 2.1 и 2.2 имеющиеся значения получим:

(2.3)

(2.4)

где - статический ток

Уравнение 2.4 разделим на и умножим на :

(2.5)

Выведем:

электрическую постоянную времени:

(2.6)

электромеханическую постоянную времени:

(2.7)

Подставим значения постоянных величин времени в уравнение 2.3 и в 2.5:

;

Запишем уравнения в дифференциальном виде:

;

откуда

;

Н
а основании двух последних уравнений составим структурную схему электродвигателя (рис.2.2).

2.2 МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРЕОБРАЗОВАТЕЛЯ

Полупроводниковый преобразователь представлен интегрирующим звеном с передаточной функцией:

;

Такое представление отражает инерционные свойства выпрямителя, обусловленные дискретным характером его работы, управляемостью вентилей. Т.о. вычертим структурную схему объекта управления (рис.2.3).

Выпишем передаточную функцию по заданию:

Передаточная функция по возмущению:

;

Рассчитаем номинальный ток и номинальную угловую скорость двигателя по следующим уравнениям:

Iн=Pн/(нUн)=2500/(0.72*110)=31,6 A

н=*nн/30=3.14*1000/30=104.7 рад/c

Сопротивление якорной цепи определяется:

Rяц=Uщ/Iд.н=Uщ/Iн=2/31.57=0.063 Ом

Rя.ц=1,26(0,27+0,2)+0,063=0,66 Ом

Lо=(1,2-1,4)*Lя.ц=1,2*0,0057=0,00684 Ом

Rо=(1,2-1,4)*Rя.ц=1,2*0,66=0,8 Ом

Суммарный момент инерции системы:

J=(1.2-2)*Jо=1,4*0,048=0,07 кг/м^2

Определяем конструктивную постоянную:

Се=(Uн-Iн*Rя.ц)/н=(110-31,57*0,66)/104.7=0.85

Определяем электромеханическую постоянную времени и электромагнитную постоянную двигателя:

Tм=JRo/Сe^2=0.07*0.8/0.85^2=0.078 c

T=Lo/Ro=0.00684/0.8=0.0098 c

3 СИНТЕЗ САУ МЕТОДОМ ПОСЛЕДОВАТЕЛЬНОЙ ОПТИМИЗАЦИИ КОНТУРОВ

Синтез – это определение структуры и параметров управляющего устройства, обеспечивающие заданные статические и динамические показатели.

Существуют следующие методы синтеза систем автоматического управления:

- метод параметрической оптимизации контуров,

- метод последовательной оптимизации контуров,

- метод модального управления,

- метод, основанный на теории оптимального управления.

В данной работе рассматриваются метод последовательной оптимизации контуров и метод модального управления.

Метод последовательной оптимизации контуров является более грубым (менее точным), т.к. он основан на радио допущениях. Причем синтез каждого контура рассматривается в отдельности без учета влияния их друг на друга. В настоящее время практически все электропривода рассчитываются данным методом.

Структурная схема системы представлена на рис.3.1.

Система автоматического управления скоростью двигателя включает в себя три контура:

контур регулирования тока, здесь:

- передаточная функция регулятора тока,

- коэффициент обратной связи по току.

km=10/(Im*Ro)=10/(2*31.57*0.8)=0.2

где

статический контур регулирования скорости

- передаточная функция статического регулятора скорости.

- сигнал задания для статического контура скорости

астатический контур регулирования скорости

- передаточная функция астатического регулятора скорости.

3.1 СИНТЕЗ КОНТУРА РЕГУЛИРОВАНИЯ ТОКА

При синтезе контура тока принимаем допущение, что не учитывается внутренняя обратная связь по ЭДС двигателя.

С
труктурная схема контура тока без учета обратной связи по скорости показана на рис. 3.2.

На основании структурной схемы можно записать:

Как видно из уравнения, регулятор тока компенсирует электромагнитную постоянную двигателя, но вносит инерционность, вызванную постоянной времени .

Передаточная функция будет иметь вид:

Характеристическое уравнение:

Принимаем корни управления согласно техническому оптимуму:

В соответствии с этим получим:

прировняв коэффициенты при одинаковых степенях p получим:

(3.1)

(3.2)

Подставив (3.1) в (3.2) получим:

m=2Toпkm=2*0.005*25*0.2=0.05 c

m=1/(2*0.005)=100

tp.m3/m=0.03 c

3.2 СИНТЕЗ СТАТИЧЕСКОГО КОНТУРА РЕГУЛИРОВАНИЯ СКОРОСТИ

С
труктурная схема контура показана на рис. 3.3.

Передаточная функция контура регулирования тока имеет вид:

но , поэтому:

(3.3)

На основании структурной схемы и выражения 3.3 запишем передаточную функцию для статического контура регулирования скорости:

При синтезе контура скорости опять делается допущение, заключающееся в том, что не учитывается коэффициент при старшей степени p, т.е.

таким образом, передаточная функция будет иметь вид:

Характеристическое уравнение имеет вид:

Приравняв коэффициенты при одинаковых степенях p получим:

1/2To=2cc  cc=1/2To=1/(2*0.005)=50

tpcc=3/cc=3/50=0.06

=10/Uн=10/110=0,091

c=kmTm/4To=(0.2*0.078)/(4*0.005*0.091)=8.6 c

3.3 СИНТЕЗ АСТАТИЧЕСКОГО КОНТУРА РЕГУЛИРОВАНИЯ СКОРОСТИ

С
труктурная схема астатического контура регулирования скорости

показана на рис.3.4.

Передаточная функция статического контура регулирования скорости имела вид:

(3.4)

На основании структурной схемы (рис. 3.4) и выражения 3.4 запишем:

Передаточная функция:

Делаем допущение, что коэффициент при старшей степени p равен нулю.

p^2+(1/4To)p+1/(4To)=p^2+2capp+2ca^2

1/4To=2ca  ca=1/8To

tpca=24To=0.12

1/(4To)=2ca^2=1/(32To^2)  =8To=8*0.005=0.04 c

Полная структурная схема системы автоматического регулирования скорости, синтезированной методом последовательной оптимизации контуров, показана на рис. 3.5.

4 СИНТЕЗ САУ МЕТОДОМ МОДАЛЬНОГО УПРАВЛЕНИЯ

Термин «модальное управление» происходит от слова moda – свободное движение.

Метод модального управления, как правило, используется для синтеза астатических САУ. В статических системах существует зависимость между статическими и динамическими свойствами системы, т.е. получив нужные динамические свойства, статические могут оказаться неудовлетворительными. Астатические системы такой проблемы не знают, т.е. получив нужные динамические свойства, статические получаются автоматически.

Структурная схема представлена на рис. 4.1. Здесь - передаточная функция задатчика интенсивности, который преобразует ступенчатый сигнал в линейный и служит для формирования свойств системы по возмущению.

4.1 СИНТЕЗ САУ БЕЗ УЛУЧШЕННЫХ ДИНАМИЧЕСКИХ ПОКАЗАТЕЛЕЙ

Структурная схема данной САУ показана на рис. 4.2. На основании структурной схемы можно записать следующее:

Передаточная функция данной системы будет иметь вид:

Прировняв коэффициенты при одинаковых степенях p можно записать:

Согласно теореме Виета характеристическое уравнение будет иметь вид:

Зададимся распределением характеристических корней по Баттерворду:

где Н – модуль (чем больше модуль, тем выше быстродействие системы); n – порядок уравнения; i – порядковый номер характеристического уравнения.

Т.о. получим:

Таким образом из вышеуказанного можно записать:

Прировняв коэффициенты при одинаковых степенях p, получим:

(4.1)

(4.2)

(4.3)

(4.4)

Из 4.1 получим:

To=0.005c

T=0.009c

H=(1/0.005+1/0.009)/2.6=119.6

Из 4.2 получим:

Tм=0.078с

п=25

k2=(3.4*119.6^2*0.078*0.005*0.009-0.078-0.005)/(25*0.078)=0.045

Из 4.3 получим:

k1=(2.6*H^3*Tм*To*T-1)/п=(2.6*119.6^3*0.078*0.005*0.009-1)/25=0.6

Из 4.4 получим:

=0.091

ko=(119.6^4*0.078*0.005*0.009)/(25*0.091)=315.7

4.2 СИНТЕЗ САУ СКОРОСТЬЮ С УЛУЧШЕННЫМИ ДИНАМИЧЕСКИМИ ПОКАЗАТЕЛЯМИ

Структурная схема данной САУ показана на рис.4.2.

Отличие данной схемы от предыдущей заключается в том, что в УУ дополнительно вводится сигнал пропорциональной производной от выходного сигнала от задатчика интенсивности с коэффициентами и . На первый взгляд такая система является физически нереализуемой из-за наличия идеальных дифференцирующих звеньев ( и). Однако на практике дело обстоит иначе. Для получения информации о первой производной выходного сигнала ЗИ нет необходимости прибегать к операции искусственного дифференцирования. Эта информация может быть получена из самого ЗИ.

Из структурной схемы можно записать:

Знаменатель передаточной функции точно такой же, как и для предыдущей системы, поэтому коэффициенты рассчитываются точно также. И они равны:

Ro=0.8 Ом

k1=0.6

k2=0.045

Здесь дополнительно необходимо рассчитать коэффициенты из условия увеличения быстродействия системы, т.е.

(4.6)

Согласно теореме Виетта получим:

(4.7)

Быстродействие системы можно увеличить за счет компенсации одной пары комплексно-сопряженных корней. В данном случае корней р_>1> и р_>4>, т.к. они расположены близко к мнимой оси.

Условие компенсации корней р_>1> и р_>4> имеет вид:

Отсюда можно получить:

H=119.6

ko=315.7

ko1/2=0.76H  1=(0.76H2)/ko=(0.76*119.6*0.022)/315.7=0.0063

В итоге получим:

5 СИНТЕЗ САУ С ИСПОЛЬЗОВАНИЕМ НАБЛЮДАТЕЛЯ

Пусть объект управления описывается уравнением состояния, записанным в матричном виде:

(5.1)

, (5.2)

где Х и U - это соответственно вектор состояния объекта управления и вектор управления; А и В - матрицы; Y - вектор измеренных координат объекта управления.

В теории управления существует понятие управляемости и наблюдаемости САУ. Причем, если объект является управляемым и наблюдаемым, то он является и индетифицируемым. То есть по входному сигналу U и измеряемому значению У можно восстановить вектор состояния объекта управления Х. Условие управляемости и наблюдаемости имеет вид:

; (5.3)

; (5.4)

То есть, ранг матрицы управляемости N_>y> наблюдаемости N_>н> должен быть равен порядку дифференциального уравнения (п), описывающего поведение объекта.

Наблюдатели или идентификаторы могут быть разомкнутыми или замкнутыми. Алгоритм работы разомкнутого наблюдателя имеет вид:

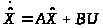(5.5)

; (5.6)

Здесь и - соответственно оценочное значение вектора состояния объекта управления и вектор выходных координат наблюдателя, то есть , а так же изменений коэффициентов матрицы А или неточного определения на этапе проектирования, такой наблюдатель обладает невысокой точностью измерения и на практике широкого распространения не получил. На практике распространение получили замкнутые наблюдатели, алгоритм функционирования которых имеет вид:

; (5.7)

Уравнение (5.2) примет вид:

;(5.8)

Соответственные значения матрицы

;(5.9)

будут определять быстродействие наблюдателя. Обычно быстродействие наблюдателя принимают в несколько раз выше быстродействия САУ , которая замыкается через наблюдатель.

Целью синтеза наблюдателя является определение коэффициентов матрицы L исходя из его быстродействия. Указанные коэффициенты можно определить методом теории модального управления.

;

12=/(2Tм)=0,091/(0,022*0,078)=53;

2/T=0.022/(0.091*0.009)=26.9;

22=1/T=111.1;

23=2/1T=0.022/(0.0063*0.009)=388;

33=1/To=1/0.005=200;

;

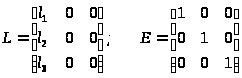tрна=(0,2-0,4)*tpc=0.012;

Hна=6/tрна=1/0,012=500;

1=688.9;

2=(2H^2-122-33(1+22)-1221/12=3950.1;

3=(H^3-12233-1223(21+2))/(1233)=95379608.5;

Составим структурную схему наблюдателя.

;

Согласно данным уравнениям строим структурную схему наблюдателя.

6. СИНТЕЗ ЦИФРОВОГО УПРАВЛЯЮЩЕГО УСТРОЙСТВА

С
труктурная схема САУ скоростью:

Нам необходимо принять время обработки информации цифровым управляющим устройством. Примем мс. За это время информация на входе ЦУУ не изменится. Структурная схема цифрового управляющего устройства показана на рисунке 5.1.

На основании структурной схемы можно записать:

; ;

Так как система астатическая, то дополнительно вводится координата x_>o> , согласно выражению

где - задающее напряжение; - коэффициент главной отрицательной обратной связи по выходной координате. Примем .

Для свободного движения уравнения состояния объекта управления и переходя от изображения к оригиналам можно записать:

Составим матрицы:

Эталонная матрица отличается от матрицы А только строкой коэффициентов

Согласно

nnbo=(п*/T)(1-/2T)=(25*0.004/0.005)(1-0.004/2*0.005)=12

(5.1)

; ; ;

откуда имеем:

процессе расчетов получим:

Коэффициенты матрицы можно определить, задавшись распределением собственных корней по Батерворту:

Согласно теореме Виетта можно записать:

это

также можно записать в матричной форме:

Т.о. получим:

Подставив полученные значения в выражения 5.1 можно определить значения коэффициентов :

7. ПРОЕКТИРОВАНИЕ ПРИНЦИПИАЛЬНОЙ СХЕМЫ УПРАВЛЯЮЩЕГО УСТРОЙСТВА

7.1 Расчет принципиальной схемы управляющего устройства, синтезированного методом последовательной оптимизации:

СУПР – система управления преобразователем;

ПР – силовая схема преобразователя;

Задатчик интенсивности регулирования на операционных усилителях DA1 DA2 и DA3 (релейные элементы и интегратор).

УТ – усилитель тока, выполняет функцию потенциальной развязки выходного сигнала с силовой схемой, так же выполняет функцию усилителя.

Регулятор скорости реализован на усилителе DA2. Регулировка тока реализована на усилителе DA5.

Зададимся

R_>4>=R_>3>=8 кОм.

R_>10>=R_>11>=33 кОм.

Для получения полного диапазона регулирования, т.е. максимальной скорости, сигнал на выходе DA6 при насыщении DA4 должен быть не менее 10В. Это условие можно записать в статическом режиме:

;

Зададимся С_>2>=0,13 мкФ.

;

Инерционное звено R_>6> - C_>3> служит для фильтрации сигнала, для помехозащищенности Т_>ф>=R_>6>C_>3>.

7.2 Проектирование принципиальной схемы методом последовательной оптимизации контуров

Регулятор тока реализован на DA6, статический регулятор скорости - на DA4, DA2 и DA7 - служат для инвертирования сигнала.

Регулятор тока называется пи-регулятором.

;

; ;

;

; зададимся ;

; ;

Регулятор скорости. Потенциометры с диодами служат для ограничения вых. напряжения статического регулятора скорости, т.е. ограничения напряжение задания тока. Для получения полного диапазона регулирования скорости, выходное напряжение на DA6 должно превышать выходной сигнал датчика тока, поступающий на R16

;

; ;

Условие выполняется:

; ; ;

Зададимся С_>2>=210^-6 ф.

7.3. Проектирование принципиальной схемы с использованием наблюдателя.

Усилитель DA5 выполняет функции только инвертора:

; ;

Сопротивление R_>1>, согласно с требованием схемы, будет определяться коэффициентом l_>3,> т.е.

;

Зададимся . Тогда ;

;

Зададимся ;

;

Зададимся ; Тогда.

ЗАКЛЮЧЕНИЕ

Оценим быстродействие системы, синтезированной методом модального управления и методом оптимизации контуров.

Время регулирования астатического контура скорости t_>рса>=24T_>0>.

Время регулирования системы синтезированной методом модального управления t_>р
му>=6,8/H.

;

если ;

;

Т.е. качество обработки линейного закона скорости выше в системе, синтезированной методом модального управления. САУ синтезированная методом модального управления является наиболее качественной.