Проектирование и расчёт микронного многооборотного микроиндикатора
Московский ордена Ленина, ордена Октябрьской Революции
и ордена Трудового Красного Знамени
ВЫСШИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ Н.Э. Баумана
РАСЧЁТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовому проекту на тему
Проектирование и расчёт микронного многооборотного микроиндикатора
2008 г.
Теоретическая часть
Описание задания
Техническое задание. Спроектировать по предложенной схеме микронный многооборотный микроиндикатор
Таблица исходных данных
Исходные данные |
Обозначение |
Единица измерения |
Вариант № 5.2. |
Пределы измерения |
l |
мм |
0...1 |
|
Цена деления шкалы |
С |
мкм |
1 |
|
Диаметр шкалы |
D |
мм |
40 |
|
Расстояние между соседними штрихами |
Х |
мм |
1,1 |
|
Допускаемая погрешность измерения |
d |
мкм |
1 |
|
Максимальное измерительное усилие |
Р |
Н |
1,5 |
|
Максимальный перепад усилий |
dР |
Н |
0,6 |
|
Интервал рабочих |
Т |
°С |
20 ± 5 |
|
Габариты прибора |
L * B * H |
мм |
100 * 65 * 30 |
Схема микронного многооборотного микроиндикатора
Краткое описание устройства
Микронный многооборотный индикатор состоит из:
Стержень (шпиндель);
Синусный механизм;
2’-3. Кулисный механизм (с ведущим кривошипом);
4. Стрелка точного отсчёта;
5. Стрелка грубого отсчёта;
Натяжной волосок;
Корпус;
Толкатель;
Силовая пружина;
Арретир;
а также зубчатых колёс Z>1> Z>2> Z>3> Z>4> Z>5>
Описание работы устройства
Многооборотный индикатор служит для измерения с высокой точностью перемещения стержня (шпинделя) 1 ( см. схема стр.4). Передача движения от измерительного стержня 1 к стрелке 4 осуществляется посредством последовательного соединения синусного механизма 1—2, кулисного механизма (с ведущим кривошипом) 2'—3 и зубчатых передач Z1Z2 и Z3Z4. Отсчёт числа полных оборотов стрелки 4 производится с помощью вспомогательной шкалы, стрелка 5 которой насажана на ось зубчатого колеса Z5, находящегося в зацеплении с трибом Z4. Силовое замыкание кинематической цепи осуществляется натяжным волоском 6. Измерительное усилие создаёт силовая пружина 9. Механизм смонтирован на плате в корпусе 7. Юстировка механизма производится при помощи эксцентриковой пятки, изменяющей длину рычага 2 синусного механизма, и накладки, изменяющей угловое положение рычага 3 кулисного механизма (на схеме не показаны). Отвод шпинделя 1 вверх осуществляется арретиром 10 через толкатель 8.
Расчёт микронного микроиндикатора
1. Синусный механизм
Синусный механизм с низшими парами (рис.1, а ) — разновидность четырёхзвенного кулисного механизма. В приборных устройствах обычно кулисный камень 2, входящий в две низшие пары, отсутствует, а его заменяет высшая пара (рис.1, б). Это повышает точность механизма и уменьшает трение. Наиболее рационально применение высшей пары с точечным контактом (сфера — плоскость), в этом случае число избыточных связей q = 0 — механизм статически определимый.
Функция положения механизма, изображённого на рис. 1(б) при ведущем рычаге 2 (зависимость линейного перемещения l ведомого звена 1 от угла поворота ведущего) выражается формулой :
l = r * sin (1)
Передаточная функция механизма в виде отношения линейной скорости кулисы и угловой скорости рычага
(2)
При малых значениях угла
,
,
следовательно, в этом случае механизм
приближённо даёт линейную зависимость
между l
и
Рис.1(а, б).
Погрешность схемы (теоретическая ошибка) при осуществлении заданной линейной зависимости между входным и выходным перемещениями найдётся из выражения :
(3)
Заменив
(4)
получим:
(5)
Для определения искомой
длины r
рычага (при заданном
максимальном перемещении l>max>
и коэффициенте пропорциональности к)
применим полином Чебышева Р>3>
(х), наименее уклоняющийся от нуля в
промежутке [ 0
x
1 ]; узлы интерполяции соответствуют
значениям корней полинома х=0; х=0,4641,
х=0,9282. Задача сводится к решению
относительно r
уравнения
, или в развернутом виде :
(6)
Решая
это уравнение, получаем r
= 5(мм); при
.
отсюда
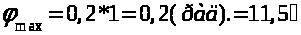
Передаточная функция механизма в виде отношения линейной скорости кулисы и угловой скорости рычага:
Для синусного механизма
Погрешность в длине рычага r .
Коэффициент влияния этой ошибки:
2. Перекос плоскости кулисы (измерительного стержня) на угол >>
Коэффициент влияния этой ошибки
3. Погрешность начального положения рычага .
Коэффициент влияния определяется по формуле :
2. Кулисный механизм
Эти механизмы могут быть четырёхзвенными с низшими парами (рис.2а) или трехзвенными с высшими кинематическими парами (рис.2б); последний вариант механизма для приборов предпочтительнее — он проще, точнее, обладает меньшим трением. Наиболее рационально применение высшей пары с точечным контактом (сфере — плоскость), в этом случае число избыточных связей q = 0 — механизм статически определимый.
Кулисные механизмы, изображенные на рис.2б, в, обеспечивают различные направления вращения ведущего и ведомого звеньев;
если же АВ > l , то эти звенья вращаются в одном направлении (рис. 2г, д).
Схемы с ведущим кривошипом (рис. 2б, г) благоприятны в отношении углов давления ( = 0 ). При ведущей кулисе (рис. 2, е, д) во избежание большого трения необходимо выполнить условие :
(7)
(знак плюс для схемы на рис. 2 е, минус — для схемы на рис. 2 д).
Во многих случаях кулисный механизм с высшей парой играет роль передаточно-множительного механизма приборного устройства и служит для приближенного воспроизведения заданной линейной зависимости между углами поворота и ведущего и ведомого звеньев при ограниченных величинах этих углов.
Рис 2(а, б, в, г, д, е)
Функция положения механизма в виде зависимости угла поворота ведомого звена от угла поворота ведущего звена (углы отсчитываются от линии АС стойки, положительные направления их показаны на чертеже) выражается следующими формулами:
при ведущем кривошипе (рис. 2, б, г).
(8)
(знак плюс для схемы на рис. 2, б, минус для схемы на рис. 2, г);
В данном случае необходимо взять знак “ – “.
Передаточная функция (мгновенное передаточное отношение) механизма находится дифференцированием формулы (8), для схемы по рис. 2, г при ведущем кривошипе :
(9)
При малых значениях угла в формуле (9):
Следовательно, в этом случае механизм обеспечивает приближенную линейную зависимость между и .
Для кулисного механизма.
1. Погрешность R в длине кривошипа.
Коэффициент влияния:
2. Погрешность L в расстоянии между осями.
Коэффициент влияния:
3. Перекос плоскости кулисы 2 на угол >1> .
Коэффициент влияния этой ошибки определяется с учётом передаточного отношения:
Погрешность начального положения ведущего звена (кулисы 2, жёстко связанной с рычагом r) уже учтена в синусном механизме.
Расчёты и вычисления
Определим кинематические параметры отсчётного устройства, обеспечивающего при заданных габаритах измерение в заданных пределах с нужной точностью с учётом заданного расстояния между соседними штрихами и цены деления шкалы.
Число штрихов на шкале точного отсчёта
N>T>> >= *D/x = 114,24 115
K= 1/(N>T>*C) 9
Стрелка делает 9 полных оборотов.
Этому соответствует 9 основных делений на шкале грубого отсчёта, стрелка которой совершает один полный оборот.
Определим диаметр шкалы грубого отсчета D>1> из условия:
D / D>1 >= К
Откуда D>1> = D/K = 40/9 = 5 (мм).
Проектирование зубчатой передачи
Передача движения от кривошипа кулисного механизма к стрелке осуществляется двухступенчатым редуктором z1-z2-z3-z4. Параметры колёс определяем исходя из условия максимального передаточного отношения при заданных габаритах. С другой стороны, следует учитывать соображения технологичности, которые накладывают ограничения на уменьшение диаметра ведомых колёс зубчатых пар. С учётом этого, диаметры d>2> и d>4> выбираем равными 4мм. Диаметры d>1> и d>3> определяются габаритами прибора: d>3>=10 мм; d>1>=20 мм.
Исходя из того, что оптимальное количество зубьев малых колёс Z>2>=Z>4>=20, произведём выбор общего модуля редуктора, учитывая, что величина модуля в данном случае не ограничивается требованиями прочности, так как редуктор переносит достаточно малую нагрузку:
m = d>4 >/ Z>4 >= 4 / 20 = 0.2
Исходя из этого, подсчитаем количество зубьев ведущих колёс:
Z>1> = d>1> / m = 20 / 0,2 = 100
Z>3> = d>3> / m = 16 / 0,2 = 80
Подсчитаем общее передаточное отношение редуктора:
i>41> = (Z>1>*Z>3>) / ( Z>2>*Z>4>) = (100*80) / (20*20) = 20
Получим величину угла зубчатого сектора Z>1> :
>z>> >= (К / i>41>) * 360° = (5 / 20) * 360° = 90°
Количество зубьев сектора:
Z = ( >z>> >/ 360°) • Z>1>= (90°/360°)*100 =25
Следовательно, длина дуги сектора:
L = >z> * *d>1 >/ 360 ° = 16 (мм).
Определим параметры зубчатого колеса Z>5 >. На каждые 9 оборотов колеса Z>4> колесо Z>5> должно делать один полный оборот, поэтому:
Z>5> = К * Z>4 >= 9 * 20 = 180.
d>5> = m * Z>5> = 0,2 * 180 = 36 (мм).
Полное передаточное отношение:
i>51>
= Z>1>
* Z>3>
* Z>4
>/ ( Z>2>
* Z>4>
* Z>5>)
=
.
Расчет суммарной погрешности всего механизма
Определим суммарную погрешность работы зубчатого редуктора.
Определяем межосевые расстояния зубчатых пар для условного модуля m*=0,5:
Определяем передаточные числа от валов III, II к валу I:
Определяем люфтовую погрешность сопряженных пар для степени точности 7H и m=0,5:
Вносим поправки на вид сопряжения, степень точности и модуль каждой пары. Колеса изготавливаются для класса точности 6G:
Находим суммарную угловую погрешность:
Упругим мертвым ходом
можно пренебречь, ввиду малой нагрузки
на выходной вал
Отсюда
суммарная величина мертвого хода
Находим собственные кинематические погрешности всех колес:
Определяем суммарную кинематическую погрешность передачи:
Находим общую погрешность передачи:
Определяем суммарную погрешность редуктора.
Пересчитываем все
погрешности передачи на линейное
перемещение стрелки
:
Синусный механизм
Кулисный механизм
Зубчатый редуктор
Находим выражение для суммарной ошибки:
где
Переводим к безразмерному
аргументу
,
получаем:
(остальные слагаемые не учитываем, так как они значительно меньше написанных).
При
:
назначим
рад, тогда получим на выходе 2,5 мм;
назначим
мм,
получим на выходе 1,6 мм (недопустимо
большие значения отклонений). Делаем
вывод о необходимости применения
компенсаторов.
Расчёт компенсаторов
Выбираем в качестве компенсаторов угловое отклонение и >1> и линейное отклонение R рычага. Принимаем степень приближающего полинома n = 3, число компенсаторов 2 , уравнение компенсируемой погрешности :
>I> = >сх> + C>1>x + С>2 >х2
Система регулировки в двух точках
Остаточная (после регулировки) погрешность:
Расчёт основных параметров силовой пружины
Предварительное проектирование пружины занимает меньше времени при использовании номограммы. По верхней части номограммы определяют диаметр d проволоки в зависимости от принятого индекса С пружины и вычисленного заранее отношения [] /Р>mах> . По нижней части номограммы определяют отношение i>p>> >/d числа рабочих витков к диаметру проволоки в зависимости от принятого индекса С и заранее вычисленного отношения G/K после этого определяют диаметр пружины и её длину по диаметру проволоки, индексу и числу витков.
Заданные эксплуатационные параметры:
Р>mах> = 2,5 (Н); dP = 0.6 (Н); P>min> = Р>m>>ах> – dP = 1.9 (Н); х = 1,1 (мм);
Материал - стальная пружинная проволока(G = 0,9 МПа, [] = 500 МПа)
1 . Подсчитаем величины, необходимые для пользования номограммой:
[] /Р>mах> = 500 / 2.5=200 (1/мм2)
G/K = G*x/dP = 1,48*10 - 5 (1/мм)
2. Задаваясь несколькими значениями индекса С, определяем по кривой [т] / P>max> = 200 в верхней части номограммы ближайшие большие диаметры проволоки, а по кривой G/K = 1,62*10 - 5 в нижней части номограммы определяем величину i>p>> >/ d .
3. Подсчитаем i >p>> >, D, D>H> и Н>0> для всех вариантов проектируемой пружины, приняв i>k> = 3 . Результаты расчётов, а также величины С и d сведём в таблицу.
I>p> = d * G/K ; D = C * d ; D>H> = D + d;
Н>о> = (i>p> * + i>k>> >) * d + x , =1,2,i>k> = 3
Вариант |
С |
d,MM |
G/K |
i>p> |
d,mm |
D>H>,MM |
H>0>,MM |
1 |
6 |
0,28 |
100 |
28 |
1,68 |
1,96 |
11,25 |
2 |
8 |
0,30 |
40 |
12 |
2,4 |
2,7 |
6,22 |
3 |
10 |
0,35 |
20 |
7 |
3,5 |
3,85 |
5 |
4 |
12 |
0,38 |
12 |
4,56 |
4,56 |
4,94 |
4,22 |
5 |
16 |
0,42 |
5 |
2,1 |
6,72 |
7,14 |
3,31 |
Наиболее соответствующим габаритам прибора следует признать 2 вариант.
Определение параметров натяжного волоска
Найдём длину, толщину ленты; шаг спирали, радиус наружного витка, и число витков спирали. Исходные данные:
наибольше угловое перемещение >mах> = 360°;
наибольшая нагрузка М>mах> = 0,048 (Н * мм);
жёсткость пружины К = 0,495 (Н/мм) ;
радиус внутреннего витка r = 3 (мм) (принимаем в соответствии с размером и конфигурацией детали, к которой крепится внутренний конец пружины).
материал пружины - сталь У10 А
модуль упругости Е = 2* 10 5 (Мпа)
предел текучести >т >= 35 (Мпа)
коэффициент запаса n>т> = 7
Расчёт:
Допустимое напряжение [>т>] = >т >/n>т> = 35/7 =5 (Мпа)
Выберем = b / h = 10
Тогда толщина ленты :
Ширина ленты: b = * h = 1,4 (мм).
Длина ленты: L = E * * h4 / 12 * K = 375 (мм).
Шаг спирали а = n * h, где n - число лент
Выберем n = 3
Тогда а = 0,6 (мм). Находим радиус наружного витка:
Число витков спирали: i = l / * (R+r) = 5.
Литература
1. «Элементы приборных устройств. Курсовое проектирование» (в 2х частях) под редакцией О.Ф. Тищенко.
2. «Справочник конструктора точного приборостроения» под редакцией И.Н. Явленского, Б.П. Тимофеева.
3. Общетехнический справочник под редакцией Е.А. Скороходова.
4. «Курсовое проектирование механизмов РЭС», под редакцией Т.И. Рощина.
5. Справочник конструктора РЭА. Под редакцией Р.Г. Варламова.
6. Справочник «Допуски и посадки», в 2х частях. В.Д. Мягков и др.
1