Поляризационная структура излученного сигнала, принятого сигнала. Когерентное объединение (накопление) сигнала в поляризационных каналах

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

кафедра ЭТТ

РЕФЕРАТ на тему:

«Поляризационная структура излученного сигнала, принятого сигнала. Когерентное объединение (накопление) сигнала в поляризационных каналах»

МИНСК, 2008

Поляризационная структура излученного сигнала

Векторное электромагнитное поле, в отличие от скалярного акустического поля, имеет поляризационную структуру. Это означает, что в фиксированной точке пространства конец вектора напряженнос­ти электрического (или магнитного) поля в плоскости поляриза­ции, перпендикулярной к направлению распространения электромагнит­ной волны, совершает вращательное движение, описывая за каждый период высокочастотного колебания траекторию, в общем случае эллиптическую, называемую годографом (рис. 1).

Эллиптически поляризованная волна (наиболее общий случай) может быть разложена на две ортогонально поляризованные составляю­щие, каждая из которых характеризуется своей амплитудой и фазой:

.

Каждая пара ортогонально поляризованных векторов и единичной длины , т.е. ортонормированных векторов, образует так называемый поляризационный базис. Поляризационных базисов может быть бесконечное множество (рис. 2). Они отлича­ются эллиптичностью (как отношением малого и большого диаметров эллипсов) и углом ориентации. Однако наиболее широкое распростра­нение получили два поляризационных базиса: линейный и круговой (рис. 3). Линейный базис составляют два пульсирующих вектора с горизонтальное и вертикальной поляризацией единичной длины (рис.3,а). Круговой базис составляют два вращающихся вектора с круговой поляризацией (правой и левой) единичной длины (рис.3,6).

Комплексные амплитуды и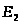, характеризующие амплитуду и фазу ортогонально поляризованных составляющих вектора , есть проекции вектора на направления ортов и соответственно, которые определяются скалярными произведениями:

,

.

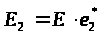К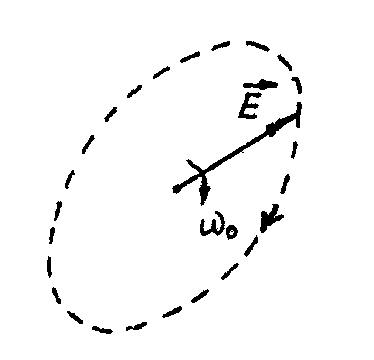
омплексные амплитуды и 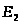можно считать комплексными координатами вектора в базисе [].

Р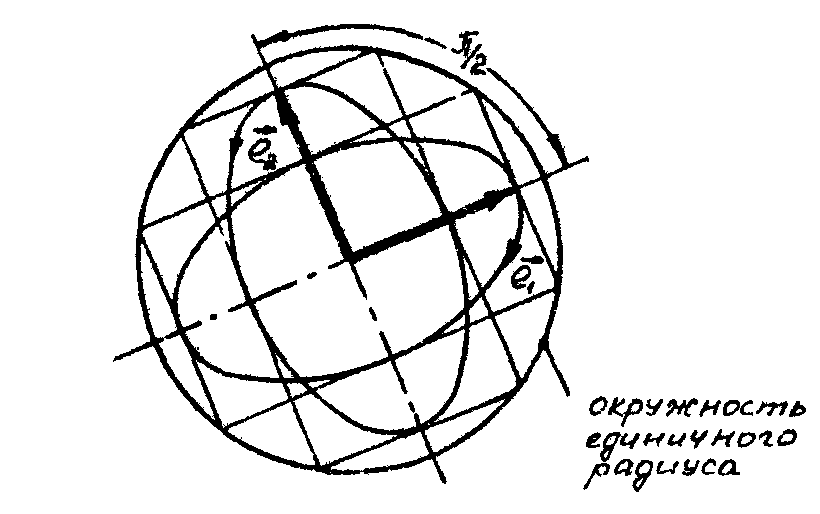
ис. 1. Годограф вектора напряженности электрического поля эллиптически поляризованной волны.

Р
ис.2. Эллиптический поляризационный базис [].

Рис. 3. Линейный (а) и круговой (б) поляризационные базисы [].

Меняя амплитуду и фазу, т.е. управляя амплитудой и фазой и 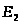ортогонально поляризованных колебаний (волн) с линейной поляризацией, получаемых, например, с помощью горизонтально и вертикально расположенных вибраторов, или с круговой поляризацией, получаемых, например, с помощью спиральных излучателей с правозаходной илевозаходной спиралью, можно получить необходимую поляризационную структуру зондирующего (излученного) сигнала и управ­лять ею. Процесс формирования некоторой эллиптически поляризо­ванной волны с помощью ортогонально поляризованных волн с круго­вой поляризацией показан на рис.4,а, а с линейной поляриза­цией - на рис.4,6. Здесь в моменты времени 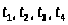с интервалом в четверть периода высокочастотного колебания пока­заны ортогонально поляризованные составляющие с учетом их комп­лексных амплитуд и 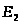. Складывая векторы напряженности элек­трического поля, соответствующие ортогонально поляризованным ком­понентам для одних и тех же моментов времени, получаем результи­рующий вектор напряженности электрического поля последователь­но в моменты времени 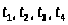, т.е. поляризационную структуру излучаемого сигнала (годограф вектора ).

Поляризационная структура принятого сигнала

При анализе поляризационной структуры принятого сигнала (от­раженного сигнала, мешающих излучений и метающих отражений) следует учитывать два явления: деполяризацию и декорреляцию поляризацион­ной структуры.

Под деполяризацией понимается изменение поляризационной струк­туры отраженного (рассеянного сигнала), т.е. изменение эллиптич­ности и ориентации годографа результирующего вектора напряженности электрического поля . Преобразование поляризации вызывается процессами обратного вторичного излучения объекта под действием наведенных на его поверхности токов проводимости (для проводников) или токов смещения (для диэлектриков). Поляризационные свойства объекта отражения (рассеяния) зависят от электрических свойств его поверхности (диэлектрической и магнитной проницаемости и про­водимости), формы,относительных размеров, ориентации относительно направления прихода облучающей волны. Поляризационные свойства объекта наблюдения характеризуются так называемой поляризационной матрицей р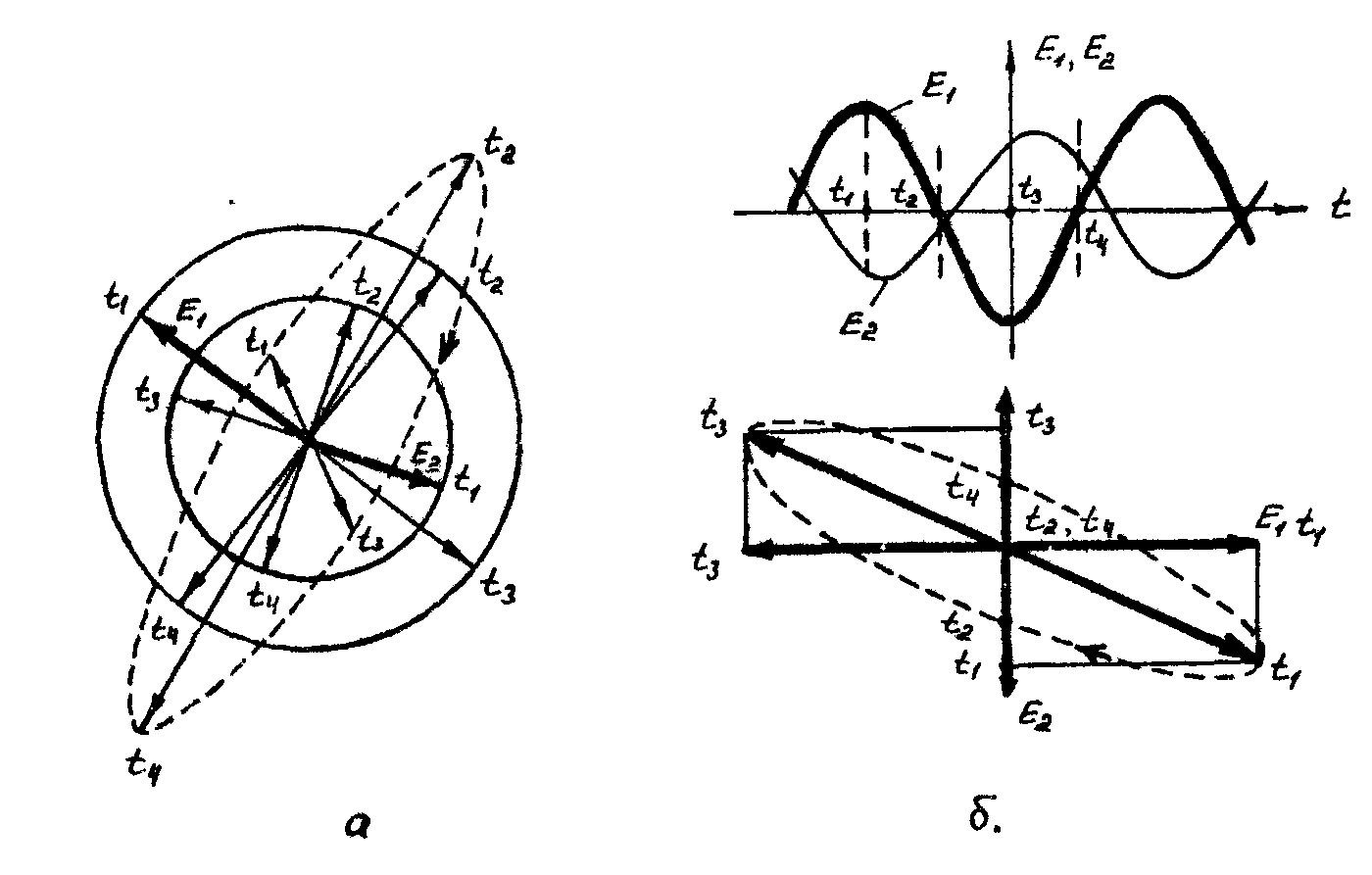
ассеяния .

Рис. 4. Результирующая эллептически поляризованная волна, сформированная из составляющих с круговой (а) и линейной (б) поляризацией.

представляющей собой совокупность четырех комплексных коэффициен­тов отражения для двух ортогонально поляризованных составляющих рассеянного поля (первый индекс коэффициента) при двух ортогонально поляризованных составляющих облучающей волны (второй индекс коэф­фициента) в некотором поляризационном базисе [].

Преобразование поляризационного состояния волны при отражении (рассеянии) может быть представлено:

- в сокращенной матричной форме

,

- в развернутой матричной форме

.

- в алгебраической форме

,

,

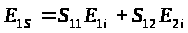где - комплексные координаты вектора отраженной и падающей волны в базисе [].

Поскольку возможно бесконечное множество различных поляризационных базисов [], существует бесконечное множество образов и 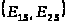, а также бесконечное множество поляризационных матриц рассеяния одного объекта наблюдения. Однако для любого объекта существует некоторый поляризационный базис , в котором матрица рассеяния приобретает диагональную форму

,

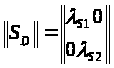когда коэффициенты отражения для перекрестных компонент равны нулю . Поляризационный базис, в котором матрица рассеяния имеет диагональную форму, называется собственным базисом объекта наблюдения (цели). Поляризации волн, совпадающих с ортами собственного базиса, называются собственными поляризациями объекта наблюдения (цели).

Рассмотрим несколько примеров поляризационных матриц рассеяния.

Пример 1. Поляризационная матрица рассеяния вибратора (рис. 2.10.5.) в линейном базисе (с горизонтальной и вертикальной поляризацией ортов):

,

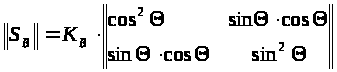где - максимальное значение коэффициента рассеяния (отра­жения) вибратора при облучении его линейно поляризованной волной, ректор поля которой параллелен оси вибратора.

Пример 2. Поляризационная матрица рассеяния сферы в любом базисе:

.

Пример 3. Поляризационная матрица рассеяния вибратора (рис. 5) в наклоненном линейном базисе, один из ортов которого параллелен оси вибратора, т.е. в собственном поляризационном ба­зисе:

.

Таким образом, вибратор является в общем случае объектом рассеяния, изменяющим поляризационную структуру облучающей волны. Объекты рассеяния радиоволн, обладающие деполяризующими свойствами, назы­ваются анизотропными в поляризационном смысле. Таких объектов -подавляющее большинство. Сфера является объектом рассеяния, не из­меняющим поляризационную структуру облучающей волны. Такие объек­ты называются изотропными в поляризационном смысле. Изотропными являются любые осесимметричные объекты, если их ось симметрии сов­падает с направлением на систему. Для изотропных объектов . Следует обратить внимание на некоторую условность понятия изотроп­ного в поляризационном смысле объекта наблюдения. Эта условность касается направления вращения вектора поля. Сохранение направления вращения вектора поля при отражении как необходимое условие изо­тропности объекта наблюдения, предполагает наблюдение обеих волн (падающей и отраженной в обратном направлении) по нормали к фронту каждой волны.

Р
ис. 2.10.5. Вибратор

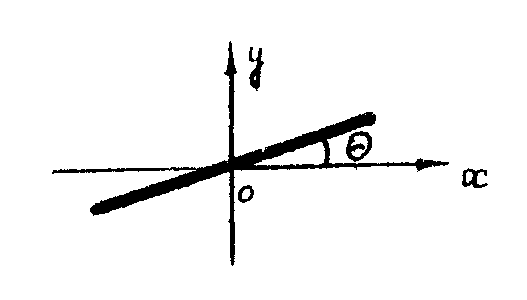
Рис. 6. Поворот базиса в плоскости поляризации

Однако в большинстве случаев предполагается наблюдение обеих волн с какой-то одной стороны (со стороны РЛС или объекта). При этом направление вращения вектора поля отражен­ной волны меняется на противоположное по сравнению с падающей волной. Эта условность, конечно, не может изменить представления об изотропности (в поляризационном смысле) объекта наблюдения.

Теперь обратимся ко второму явлений при отражении электромаг­нитной волны - декорреляции ее поляризационной структуры. Прежде всего отметим, что отраженная волна является линейным преобразова­нием падающей волны, причем свойства этого линейного преобразования определяются поляризованной матрицей рассеяния:

.

Данное обстоятельство свидетельствует о том, что четыре ком­поненты отраженного сигнала, соответствующие двум взаимно ортогональным поляризациям на прием при двух взаимно ортогональных поляризациях на излучение

,

,

,

,

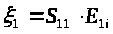являются сильно коррелированными, т.е., функционально линейно за­висимыми, если соответствующие комплексные амплитуды взаимно орто­гональных по поляризации составляющих падающего поля и являются сильно коррелированными, а также если объект наблюдения (цель) в поляризационном смысле является стабильным, т.е. пара­метры его поляризационной матрицы рассеяния не изменяются (не флуктуируют) случайным образом, а если и изменяются, то "дружно". Последнее характерно для целей (объектов наблюдения) с жесткой конструкцией, у которых положение в пространствеодних отража­телей, определяющих компоненту с одной поляризацией, зависит от расположения других отражателей, определяющих компоненту с ортого­нальной поляризацией.

Напротив, если объект наблюдения имеет нежесткую или "мягкую" конструкцию, например, совокупность пространственно распределен­ных элементарных отражателей, когда положение в пространстве одних отражателей не зависит от расположения других и эти отражатели являются анизотропными в поляризационном смысле, то приведенные выше четыре компоненты рассеянного поля 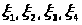оказы­ваются некоррелированными, а рассеянная волна хаотически поляризо­ванной (неполяризованной). Такая ситуация характерна для мешающих отражений от объемно или поверхностно распределенных отражателей, обладающих свойством поляризационной анизотропности.

В случае поляризационно изотропных отражателей, обладающих свойством осевой симметрии по направлению на РЛС, две компоненты рассеянного поля и принципиально отсутствуют, поскольку 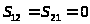, а компоненты и рассеянного поля с учетом равенства диагональных элементов матрицы рассеяния 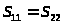будут сильно коррелированными, если сильно коррелированными явля­ются комплексные амплитуды падающего поля и . Эта си­туация характерна для объемно распределенных гидрометеоров (дождь, снег, туман, град, пыль), отражатели которых имеют осесимметричную (как правило, сферическую) форму.

Таким образом, при анализе корреляционных свойств ортогональ­но поляризованных составляющих отраженного (рассеянного) сигнала или мешающих отражений следует учитывать во взаимосвязи ряд факто­ров:

- степень жесткости конструкции объекта наблюдения,

- степень поляризационной изотропности элементарных отражате­лей, из которых состоит объект наблюдения;

- степень коррелированности комплексных амплитуд и падающего поля.

Принципы поляризационной обработки сигналов на фоне помех

Под поляризационной обработкой понимается некоторый способ объединения поляризационных каналов многоканальной по поляризации системы. Принципы поляризационной обработки можно сформулировать на основании общих принципов пространственно-временной обработки:

- подавление помех путем междуканального вычитания коррели­рованных ортогонально поляризованных составляющих мешающих колебаний (излучений и отражений;

- накопление сигнала путем междуканального сложения (коге­рентного или некогерентного) коррелированных ортогонально поляри­зованных составляющих отраженного сигнала.

Когерентное объединение (накопление) сигнала в поляризационных каналах.

Основой когерентного объединения сигнала в поляризационных каналах многоканальной по поляризации РЛС является его сильная межканальная корреляция, характерная для объектов наблюдения с жесткой конструкцией. При этом оптимальная процедура объединения сигналов с разных каналов сводится к их взвешенному когерентному накоплению (рис. 7).

Максимально возможная эффективность когерентного поляризацион­ного объединения сигналов определяется числом поляризационных ка­налов :

Полный поляризационный прием подразумевает наличие четырех поляризационных составляющих принятого сигнала .

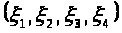Неполный поляризационный прием подразумевает наличие двух поляризационных составляющих принятого сигнала : нечетных или четных.

Некогерентное объединение (накопление) сигнала в поляризационных каналах.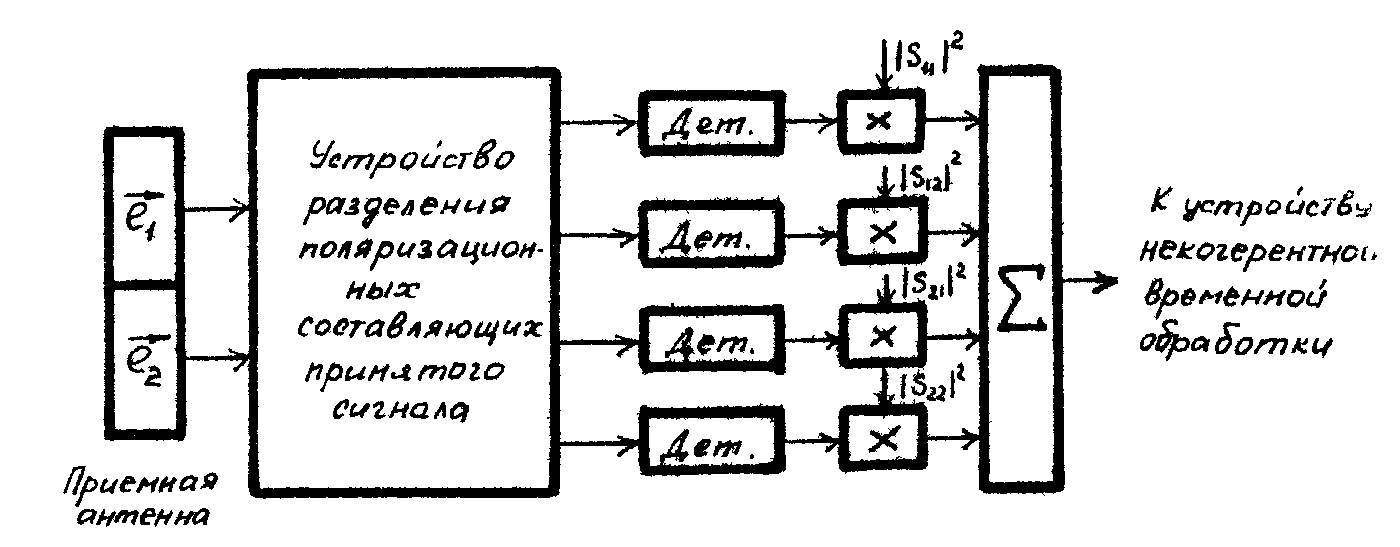
Оптимальная процедура некогерентного объединения сигналов с разных каналов сводится к их взвешенному некогерентному накоплению (рис.8).

Р
ис. 7. Схема когерентного объединения сигнала в поляризационных каналах. Рис. 8. Схема некогерентного объединения сигнала в поляризационных каналах.

Максимально возможная эффективность некогерентного объединения поляризационных каналов уступает когерентному.

ЛИТЕРАТУРА

Охрименко А.Е. Основы извлечения, обработки и передачи информации. (В 6 частях). Минск, БГУИР, 2004.

Девятков Н.Д., Голант М.Б., Реброва Т.Б.. Радиоэлектроника и медицина. –Мн. – Радиоэлектроника, 2002.

Медицинская техника, М., Медицина 1996-2000 г.

Сиверс А.П. Проектирование радиоприемных устройств, М., Радио и связь, 2006.

Чердынцев В.В. Радиотехнические системы. – Мн.: Высшая школа, 2002.

Радиотехника и электроника. Межведоств. темат. научн. сборник. Вып. 22, Минск, БГУИР, 2004.